Skip to main content
SpringerLink
Log in

The mechanical response of nanobeams considering the flexoelectric phenomenon in the temperature environment

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

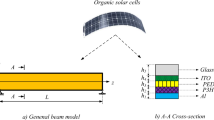
This article employs the novel shear strain theory for the first time to investigate the static bending and static buckling responses of nanobeams affected by the flexoelectric effect in a temperature environment. Consideration is given to the effect of applied voltage and rotation on the beam's fixed axis. The calculation formulas are based on the finite element method; the equilibrium equation is derived from Hamilton's principle, where charge polarization is considered via the strain gradient; and the voltage applied to the beam makes the electric field calculation expression significantly more complex than previously reported. This increases the realism of the research results. This study also investigated the effect of a series of rotational parameters, applied voltage, temperature, and boundary conditions on the nanobeams' mechanical response. The paper demonstrates through calculation results that the influence of the applied voltage increases the beam's load capacity. This parameter can be used to adjust the beam's bending response, which is the foundation of practical application.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data availability

Data used to support the findings of this study are included in the article.

References

  1. Zhang, M., Zhou, Z.: Bending and vibration analysis of flexoelectric beam structure on linear elastic substrates. Micromachines 13(6), 915 (2022). https://doi.org/10.3390/mi13060915

    Article  PubMed  PubMed Central  Google Scholar 

  2. Shingare, K.B., Naskar, S.: Compound influence of surface and flexoelectric effects on static bending response of hybrid composite nanorod. J. Strain Anal. Eng. Des. 58(2), 73–90 (2023). https://doi.org/10.1177/03093247221096518

    Article  Google Scholar 

  3. Abdelrahman, A.A., Saleem, H.A., Abdelhaffez, G.S., Eltaher, M.A.: On bending of piezoelectrically layered perforated nanobeams embedded in an elastic foundation with flexoelectricity. Mathematics 11(5), 1162 (2023). https://doi.org/10.3390/math11051162

    Article  Google Scholar 

  4. Thai, T.Q., Zhuang, X., Rabczuk, T.: Curved flexoelectric and piezoelectric micro-beams for nonlinear vibration analysis of energy harvesting. Int. J. Solids Struct. 264, 112096 (2023). https://doi.org/10.1016/j.ijsolstr.2022.112096

    Article  Google Scholar 

  5. Yan, Z., Jiang, L.: Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D Appl. Phys. 46(35), 355502 (2013). https://doi.org/10.1088/0022-3727/46/35/355502

    Article  CAS  Google Scholar 

  6. Zhang, R., Liang, X., Shen, S.: A Timoshenko dielectric beam model with flexoelectric effect. Meccanica 51(5), 1181–1188 (2016). https://doi.org/10.1007/s11012-015-0290-1

    Article  MathSciNet  Google Scholar 

  7. Yue, Y.M., Xu, K.Y., Chen, T.: A micro scale Timoshenko beam model for piezoelectricity with flexoelectricity and surface effects. Compos. Struct. 136, 278–286 (2016). https://doi.org/10.1016/j.compstruct.2015.09.046

    Article  Google Scholar 

  8. Li, X., Luo, Y.: Flexoelectric effect on vibration of piezoelectric microbeams based on a modified couple stress theory. Shock. Vib. (2017). https://doi.org/10.1155/2017/4157085

    Article  Google Scholar 

  9. Nguyen, B.H., Nanthakumar, S.S., Zhuang, X., Wriggers, P., Jiang, X., Rabczuk, T.: Dynamic flexoelectric effect on piezoelectric nanostructures. Eur. J. Mech. A/Solids 71, 404–409 (2018). https://doi.org/10.1016/j.euromechsol.2018.06.002

    Article  ADS  MathSciNet  Google Scholar 

  10. Arefi, M., Pourjamshidian, M., Ghorbanpour-Arani, A., Rabczuk, T.: Influence of flexoelectric, small-scale, surface and residual stress on the nonlinear vibration of sigmoid, exponential and power-law FG Timoshenko nano-beams. J. Low Freq. Noise Vib. Act. Control 38(1), 122–142 (2019)

    Article  Google Scholar 

  11. Duc, D.H., Van Thom, D., Cong, P.H., Van Minh, P., Nguyen, N.X.: Vibration and static buckling behavior of variable thickness flexoelectric nanoplates. Mech. Based Des. Struct. Mach. (2022). https://doi.org/10.1080/15397734.2022.2088558

    Article  Google Scholar 

  12. Phung, V.M.: Static bending analysis of nanoplates on discontinuous elastic foundation with flexoelectric effect. J. Sci. Tech. 17(5), 47–57 (2022). https://doi.org/10.56651/lqdtu.jst.v17.n05.529

    Article  MathSciNet  Google Scholar 

  13. Tien, D.M., Van Thom, D., Van Minh, P., Tho, N.C., Doan, T.N., Mai, D.N.: The application of the nonlocal theory and various shear strain theories for bending and free vibration analysis of organic nanoplates. Mech. Based Des. Struct. Mach. (2023). https://doi.org/10.1080/15397734.2023.2186893

    Article  Google Scholar 

  14. Kloda, L., Warminski, J.: “Nonlinear longitudinal–bending–twisting vibrations of extensible slowly rotating beam with tip mass. Int. J. Mech. Sci. (2022). https://doi.org/10.1016/j.ijmecsci.2022.107153

    Article  Google Scholar 

  15. Wu, X., Jiao, Y., Chen, Z.: An analytical model of a rotating radial cantilever beam considering the coupling between bending, stretching, and torsion. J. Vib. Acoust. Trans. ASME (2022). https://doi.org/10.1115/1.4051494

    Article  Google Scholar 

  16. Moon, H., Cho, H., Theodossiades, S., Kim, T.: Development of an anisotropic co-rotational beam model including variable cross-section. Mech. Adv. Mater. Struct. (2022). https://doi.org/10.1080/15376494.2021.2015810

    Article  Google Scholar 

  17. Valverde-Marcos, B., Muñoz-Abella, B., Rubio, P., Rubio, L.: Influence of the rotation speed on the dynamic behaviour of a cracked rotating beam. Theor. Appl. Fract. Mech. 117, 103209 (2022). https://doi.org/10.1016/j.tafmec.2021.103209

    Article  Google Scholar 

  18. Van Dung, N., Tho, N.C., Ha, N.M., Hieu, V.T.: On the finite element model of rotating functionally graded graphene beams resting on elastic foundation. Math. Probl. Eng. (2021). https://doi.org/10.1155/2021/1586388

    Article  Google Scholar 

  19. Pradhan, S.C., Murmu, T.: Application of nonlocal elasticity and DQM in the flapwise bending vibration of a rotating nanocantilever. Phys. E Low-Dimens. Syst. Nanostruct. 42(7), 1944–1949 (2010). https://doi.org/10.1016/j.physe.2010.03.004

    Article  ADS  CAS  Google Scholar 

  20. Li, L., Zhang, D.G., Zhu, W.D.: Free vibration analysis of a rotating hub-functionally graded material beam system with the dynamic stiffening effect. J. Sound Vib. 333(5), 1526–1541 (2014). https://doi.org/10.1016/j.jsv.2013.11.001

    Article  ADS  Google Scholar 

  21. Dehrouyeh-Semnani, A.M., BehboodiJouybari, M., Dehrouyeh, M.: On size-dependent lead-lag vibration of rotating microcantilevers. Int. J. Eng. Sci. 101, 50–63 (2016). https://doi.org/10.1016/j.ijengsci.2015.12.009

    Article  MathSciNet  Google Scholar 

  22. Das, D.: Free vibration and buckling analyses of geometrically non-linear and shear-deformable FGM beam fixed to the inside of a rotating rim. Compos. Struct. 179, 628–645 (2017). https://doi.org/10.1016/j.compstruct.2017.07.051

    Article  Google Scholar 

  23. Babaei, A., Yang, C.X.: Vibration analysis of rotating rods based on the nonlocal elasticity theory and coupled displacement field. Microsyst. Technol. 25(3), 1077–1085 (2019). https://doi.org/10.1007/s00542-018-4047-3

    Article  Google Scholar 

  24. Li, L., Liao, W.H., Zhang, D., Zhang, Y.: Vibration control and analysis of a rotating flexible FGM beam with a lumped mass in temperature field. Compos. Struct. 208, 244–260 (2019). https://doi.org/10.1016/j.compstruct.2018.09.070

    Article  Google Scholar 

  25. Chen, D., Feng, K., Zheng, S.: Flapwise vibration analysis of rotating composite laminated Timoshenko microbeams with geometric imperfection based on a re-modified couple stress theory and isogeometric analysis. Eur. J. Mech. A/Solids 76, 25–35 (2019). https://doi.org/10.1016/j.euromechsol.2019.03.002

    Article  ADS  MathSciNet  Google Scholar 

  26. Atanasov, M.S., Stojanović, V.: Nonlocal forced vibrations of rotating cantilever nano-beams. Eur. J. Mech. A/Solids 79, 103850 (2020). https://doi.org/10.1016/j.euromechsol.2019.103850

    Article  ADS  MathSciNet  Google Scholar 

  27. Tho, N.C., Thanh, N.T., Tho, T.D., Van Minh, P., Hoa, L.K.: Modelling of the flexoelectric effect on rotating nanobeams with geometrical imperfection. J. Braz. Soc. Mech. Sci. Eng. (2021). https://doi.org/10.1007/s40430-021-03189-w

    Article  Google Scholar 

  28. Chi Tho, N., Van Thom, D., Hong Cong, P., Zenkour, A.M., Hong Doan, D., Van Minh, P.: Finite element modeling of the bending and vibration behavior of three-layer composite plates with a crack in the core layer. Compos. Struct. 305, 116529 (2023). https://doi.org/10.1016/j.compstruct.2022.116529

    Article  Google Scholar 

  29. Van Phung, M., Nguyen, D.T., Doan, L.T., Van Nguyen, D., Van Duong, T.: Numerical investigation on static bending and free vibration responses of two-layer variable thickness plates with shear connectors. Iran. J. Sci. Technol. Trans. Mech. Eng. 46(4), 1047–1065 (2022). https://doi.org/10.1007/s40997-021-00459-9

    Article  Google Scholar 

  30. Tuan, L.T., Dung, N.T., Van Thom, D., Van Minh, P., Zenkour, A.M.: Propagation of non-stationary kinematic disturbances from a spherical cavity in the pseudo-elastic cosserat medium. Eur. Phys. J. Plus (2021). https://doi.org/10.1140/epjp/s13360-021-02191-4

    Article  Google Scholar 

  31. Nguyen Thai, D., Van Minh, P., Phan Hoang, C., Ta Duc, T., Nguyen Thi Cam, N., Nguyen Thi, D.: Bending of symmetric sandwich FGM beams with shear connectors. Math. Probl. Eng. 1, 2–1 (2021). https://doi.org/10.1155/2021/7596300

    Article  MathSciNet  Google Scholar 

  32. Van Thom, D., Duc, D.H., Van Minh, P., Tung, N.S.: Finite element modelling for vibration response of cracked stiffened fgm plates. Vietnam J. Sci. Technol. 58(1), 119–129 (2020). https://doi.org/10.15625/2525-2518/58/1/14278

    Article  Google Scholar 

  33. Nguyen, H.N., Tan, T.C., Luat, D.T., Phan, V.D., Van Thom, D., Van Minh, P.: Research on the buckling behavior of functionally graded plates with stiffeners based on the third-order shear deformation theory. Materials (Basel) 12(8), 1262 (2019). https://doi.org/10.3390/ma12081262

    Article  ADS  CAS  PubMed  Google Scholar 

  34. Nguyen, H.N., Hong, T.T., Vinh, P.V., Thom, D.V.: An efficient beam element based on Quasi-3D theory for static bending analysis of functionally graded beams. Materials 12(13), 2198 (2019). https://doi.org/10.3390/ma12132198

    Article  ADS  PubMed  PubMed Central  Google Scholar 

  35. Quang, D.V., Doan, T.N., Luat, D.T., Thom, D.V.: Static analysis and boundary effect of FG-CNTRC cylindrical shells with various boundary conditions using quasi-3D shear and normal deformations theory. Structures 44, 828–850 (2022). https://doi.org/10.1016/j.istruc.2022.08.039

    Article  Google Scholar 

  36. Do, V.T., Pham, V.V., Nguyen, H.N.: On the development of refined plate theory for static bending behavior of functionally graded plates. Math. Probl. Eng. 1, 2836763 (2020). https://doi.org/10.1155/2020/2836763

    Article  MathSciNet  Google Scholar 

  37. Do, T.V., Bui, T.Q., Yu, T.T., Pham, D.T., Nguyen, C.T.: Role of material combination and new results of mechanical behavior for FG sandwich plates in thermal environment. J. Comput. Sci. 21, 164–181 (2017). https://doi.org/10.1016/j.jocs.2017.06.015

    Article  MathSciNet  Google Scholar 

  38. Dat, P.T., Van Thom, D., Luat, D.T.: Free vibration of functionally graded sandwich plates with stiffeners based on the third-order shear deformation theory. Viet. J. Mech. 38(2), 103–122 (2016). https://doi.org/10.15625/0866-7136/38/2/6730

    Article  Google Scholar 

  39. Yu, T., et al.: On the thermal buckling analysis of functionally graded plates with internal defects using extended isogeometric analysis. Compos. Struct. 136, 684–695 (2016). https://doi.org/10.1016/j.compstruct.2015.11.002

    Article  Google Scholar 

  40. Bui, T.Q., et al.: On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos. Part B Eng. 92, 218–241 (2016). https://doi.org/10.1016/j.compositesb.2016.02.048

    Article  CAS  Google Scholar 

  41. Van Thom, D., Duc, D.H., Van Minh, P., Tung, N.S.: Finite element modelling for free vibration response of cracked stiffened fgm plates. Vietnam J. Sci. Technol. 58(1), 119 (2020). https://doi.org/10.15625/2525-2518/58/1/14278

    Article  Google Scholar 

  42. Duc, N.D., Trinh, T.D., Van Do, T., Doan, D.H.: On the buckling behavior of multi-cracked FGM plates. Lect. Notes Mech. Eng. PartF3, 29–45 (2018). https://doi.org/10.1007/978-981-10-7149-2_3

    Article  Google Scholar 

  43. Van Do, T., Hong Doan, D., Chi Tho, N., Dinh Duc, N.: Thermal buckling analysis of cracked functionally graded plates. Int. J. Struct. Stab. Dyn. (2022). https://doi.org/10.1142/S0219455422500894

    Article  MathSciNet  Google Scholar 

  44. Tuyen, B.V., Du, N.D.: Analytic solutions for static bending and free vibration analysis of FG nanobeams in thermal environment. J. Therm. Stress. (2023). https://doi.org/10.1080/01495739.2023.2211642

    Article  Google Scholar 

  45. Bui, T.Q., Doan, D.H., Van Do, T., Hirose, S., Duc, N.D.: High frequency modes meshfree analysis of Reissner–Mindlin plates. J. Sci. Adv. Mater. Dev. 1(3), 400–412 (2016). https://doi.org/10.1016/j.jsamd.2016.08.005

    Article  Google Scholar 

  46. Duc, D.H., Thom, D.V., Phuc, P.M.: Buckling analysis of variable thickness cracked nanoplatesconsiderting the flexoelectric effect. Trans. Commun. Sci. J. 73(5), 470–485 (2022). https://doi.org/10.47869/tcsj.73.5.3

    Article  Google Scholar 

  47. Tho, N.C., Ta, N.T., Thom, D.V.: New numerical results from simulations of beams and space frame systems with a tuned mass damper. Material 12(8), 1329 (2019). https://doi.org/10.3390/ma12081329

    Article  ADS  Google Scholar 

  48. Doan, T.N., Thom, D.V., Thanh, N.T., Van Chuong, P., Tho, N.C., Ta, N.T., Nguyen, H.N.: Analysis of stress concentration phenomenon of cylinder laminated shells using higher-order shear deformation Quasi-3D theory. Compos. Struct. 232, 111526 (2020). https://doi.org/10.1016/j.compstruct.2019.111526

    Article  Google Scholar 

  49. Hoai, N.V., Doan, D.H., Khoa, N.M., Do, T.V., Tran, H.T.: Phase-field buckling analysis of cracked stiffened functionally graded plates. Compos. Struct. 217, 50–59 (2019). https://doi.org/10.1016/j.compstruct.2019.03.014

    Article  Google Scholar 

  50. Tuyen, B.V.: Free vibration behaviors of nanoplates resting on viscoelastic medium. Arab. J. Scien. Eng. (2022). https://doi.org/10.1007/s13369-022-07500-2

    Article  Google Scholar 

  51. Minh, P.P., Do, T.V., Duc, D.H., Duc, N.D.: The stability of cracked rectangular plate with variable thickness using phase field method. Thin-Walled Struct. 129, 157–165 (2018). https://doi.org/10.1016/j.tws.2018.03.028

    Article  Google Scholar 

  52. Tuyen, B.V.: Vibration response of bamboo-reinforced composite beams. J. Vib. Eng. Technol. (2023). https://doi.org/10.1007/s42417-023-00998-2

    Article  Google Scholar 

  53. Doan, D.H., Zenkour, A.M., Thom, D.V.: Finite element modeling of free vibration of cracked nanoplates with flexoelectric effects. Eur. Phys. J. Plus. 137, 447 (2022). https://doi.org/10.1140/epjp/s13360-022-02631-9

    Article  Google Scholar 

  54. Do, T.V., Doan, D.H., Duc, N.D., Bui, T.Q.: Phase-field thermal buckling analysis for cracked functionally graded composite plates considering neutral surface. Compos. Struct. 182, 542–548 (2017). https://doi.org/10.1016/j.compstruct.2017.09.059

    Article  Google Scholar 

  55. Anh, T.T., Do, T.V., Tien, D.P., Duc, N.D.: The effects of strength models in numerical study of metal plate destruction by contact explosive charge. Mech. Adv. Mater. Struct. 26(8), 661–670 (2019). https://doi.org/10.1080/15376494.2017.1410907

    Article  Google Scholar 

  56. Doan, D.H., Do, T.V., Pham, P.M., Duc, N.D.: Validation simulation for free vibration and buckling of cracked Mindlin plates using phase-field method. Mech. Adv. Mater. Struct. 26(12), 1018–1027 (2019). https://doi.org/10.1080/15376494.2018.1430262

    Article  Google Scholar 

  57. Tuan, L.T., Van Dung, N., Van Minh, P., Tan, B.D., Van Thom, D., Zenkour, A.M.: Analysis of the stress–strain state of the elastic moment medium when a spherical cavity diffracts the wave. J. Vib. Eng. Technol. (2023). https://doi.org/10.1007/s42417-023-01155-5

    Article  Google Scholar 

  58. Lieu, P.V., Luu, G.T.: Static bending, free and forced vibration responses of organic nanobeams in a temperature environment. Arch. Appl. Mech. 93, 3947–3963 (2023). https://doi.org/10.1007/s00419-023-02469-2

    Article  Google Scholar 

  59. Zhang, G.Y., He, Z.Z., Gao, X.L., Zhou, H.W.: Band gaps in a periodic electro-elastic composite beam structure incorporating microstructure and flexoelectric effects. Arch. Appl. Mech. 93, 245–260 (2023). https://doi.org/10.1007/s00419-021-02088-9

    Article  ADS  Google Scholar 

  60. Qu, Y., Jin, F., Yang, J.: Torsion of a flexoelectric semiconductor rod with a rectangular cross section. Arch. Appl. Mech. 91, 2027–2038 (2021). https://doi.org/10.1007/s00419-020-01867-0

    Article  ADS  Google Scholar 

  61. Ghobadi, A., Beni, Y.T., Golestanian, H.: Nonlinear thermo-electromechanical vibration analysis of size-dependent functionally graded flexoelectric nano-plate exposed magnetic field. Arch. Appl. Mech. 90, 2025–2070 (2020). https://doi.org/10.1007/s00419-020-01708-0

    Article  ADS  Google Scholar 

  62. Yang, W., Hu, T., Liang, X., Shen, S.: On band structures of layered phonic crystals with flexoelectricity. Arch. Appl. Mech. 88, 629–644 (2018). https://doi.org/10.1007/s00419-017-1332-z

    Article  ADS  Google Scholar 

  63. Thai, H.T., Choi, D.H.: Finite element formulation of various four unknown shear deformation theories for functionally graded plates. Finite Elem. Anal. Des. 75, 50–61 (2013). https://doi.org/10.1016/j.finel.2013.07.003

    Article  MathSciNet  Google Scholar 

  64. Touratier, M.: An efficient standard plate theory. Int. J. Eng. Sci. 29(8), 901–916 (1991). https://doi.org/10.1016/0020-7225(91)90165-Y

    Article  Google Scholar 

  65. Thai, L.M., Luat, D.T., Phung, V.B., Van Minh, P., Van Thom, D.: Finite element modeling of mechanical behaviors of piezoelectric nanoplates with flexoelectric effects. Arch. Appl. Mech. 92(1), 163–182 (2022). https://doi.org/10.1007/s00419-021-02048-3

    Article  ADS  Google Scholar 

  66. Shu, L., Wei, X., Pang, T., Yao, X., Wang, C.: Symmetry of flexoelectric coefficients in crystalline medium. J. Appl. Phys. (2011). https://doi.org/10.1063/1.3662196

    Article  Google Scholar 

  67. Yang, W., Liang, X., Shen, S.: Electromechanical responses of piezoelectric nanoplates with flexoelectricity. Acta Mech. 226(9), 3097–3110 (2015). https://doi.org/10.1007/s00707-015-1373-8

    Article  MathSciNet  Google Scholar 

  68. Chen, W.Q., Lü, C.F., Bian, Z.G.: A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Appl. Math. Model. 28(10), 877–890 (2004). https://doi.org/10.1016/j.apm.2004.04.001

    Article  Google Scholar 

  69. Reddy, J.N.: Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 45(2–8), 288–307 (2007). https://doi.org/10.1016/j.ijengsci.2007.04.004

    Article  CAS  Google Scholar 

  70. Aydogdu, M.: A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Phys. E Low-Dimens. Syst. Nanostruct. 41(9), 1651–1655 (2009). https://doi.org/10.1016/j.physe.2009.05.014

    Article  ADS  Google Scholar 

  71. Eltaher, M.A., Alshorbagy, A.E., Mahmoud, F.F.: Vibration analysis of Euler–Bernoulli nanobeams by using finite element method. Appl. Math. Model. 37(7), 4787–4797 (2013). https://doi.org/10.1016/j.apm.2012.10.016

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Applied Physics, Science and Technology Advanced Institute, Van Lang University, Ho Chi Minh City, Vietnam

    Gia Thien Luu

  2. Faculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam

    Gia Thien Luu

  3. Division of Mechanics, Civil Engineering Department, Akdeniz University, Antalya, Turkey

    Ömer Civalek

  4. China Medical University Hospital, China Medical University, Taichung, 404327, Taiwan

    Ömer Civalek

  5. Thuyloi University, 175 Tay Son, Dong Da, Hanoi, Vietnam

    Bui Van Tuyen

Authors
  1. Gia Thien Luu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ömer Civalek
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bui Van Tuyen
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Dr Gia Thien Luu was involved in methodology and supervision and wrote the manuscript. Prof. Ömer Civalek prepared all figures, solved the result number, and contributed to visualization Dr. Bui Van Tuyen contributed to methodology, solved the result number, and wrote the manuscript All authors reviewed the manuscript

Corresponding author

Correspondence to Bui Van Tuyen.

Ethics declarations

Conflicts of interest

All authors declare that there is no conflict of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

$$ E_{z1} = - \frac{1}{{k_{2}^{2} h}}\left( \begin{gathered} - 2\cosh \left( \frac{z}{h} \right)\varepsilon_{\rm{s}} f_{14} h^{3} k_{1} k_{2}^{2} - \sinh \left( \frac{z}{h} \right)e_{31} \varepsilon_{\rm{s}} h^{4} k_{1} k_{2}^{2} \hfill \\ + k_{2}^{2} \left\{ {k_{3} e_{31} z\left\{ {\varepsilon_{\rm{s}} .\left( {k_{0} + 1} \right) + \varepsilon_{\rm{b}} } \right\}h + \psi } \right\} \hfill \\ \end{gathered} \right); $$
$$ E_{z2} = - \frac{{\sinh \left( {\frac{{k_{2} h}}{2}} \right)}}{{k_{2}^{2} b_{33} h\left( {e^{{2k_{2} h}} - 1} \right)}}\left( \begin{gathered} \left( \begin{gathered} \varepsilon_{\rm{s}} hf_{14} \cosh \left( \frac{1}{2} \right) \hfill \\ - 4\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) + \left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ + 2\left( \begin{gathered} \frac{1}{2}\varepsilon_{\rm{s}} hf_{14} \cosh \left( \frac{1}{2} \right) \hfill \\ - 2\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) + \frac{1}{2}\left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right); $$
$$ E_{z3} = \frac{{e^{{ - k_{2} z}} }}{{2\left( {e^{{2k_{2} h}} - 1} \right)k_{2} b_{33} }}\left( \begin{gathered} \left( \begin{gathered} - 2h\varepsilon_{\rm{s}} \left( {b_{33} e_{31} hk_{1} - \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right) \hfill \\ - 4\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) \hfill \\ + 2k_{3} e_{31} \left\{ {\varepsilon_{sx} .\left( {k_{0} + 1} \right) + \varepsilon_{\rm{b}} } \right\}b_{33} + \left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ + 2\left( \begin{gathered} h\varepsilon_{\rm{s}} \left( {b_{33} e_{31} hk_{1} + \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right) \hfill \\ - 2\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) \hfill \\ - k_{3} e_{31} \left\{ {\varepsilon_{\rm{s}} .\left( {k_{0} + 1} \right) + \varepsilon_{\rm{b}} } \right\}b_{33} + \frac{1}{2}\left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right) $$
$$ E_{z4} = - \frac{{e^{{k_{2} z}} }}{{2\left( {e^{{2k_{2} h}} - 1} \right)k_{2} b_{33} }}\left( \begin{gathered} \left( \begin{gathered} - 2h\varepsilon_{\rm{s}} \left( {b_{33} e_{31} hk_{1} + \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right) \hfill \\ + 4\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) \hfill \\ + 2k_{3} e_{31} \left\{ {\varepsilon_{\rm{s}} .\left( {k_{0} + 1} \right) + \varepsilon_{\rm{b}} } \right\}b_{33} - \left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ + 2\left( \begin{gathered} h\varepsilon_{\rm{s}} \left( {b_{33} e_{31} hk_{1} - \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right) \hfill \\ + 2\varepsilon_{\rm{s}} h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right) \hfill \\ - k_{3} e_{31} \left\{ {\varepsilon_{\rm{s}} .\left( {k_{0} + 1} \right) + \varepsilon_{\rm{b}} } \right\}b_{33} - \frac{1}{2}\left\{ {\varepsilon_{\rm{s}} + \varepsilon_{\rm{b}} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right) $$

with

$$ k_{0} = \cosh \left( \frac{1}{2} \right);\;\;k_{1} = \frac{1}{{\kappa_{33} h^{2} - b_{33} }};\;\;k_{2} = \sqrt {\frac{{k_{33} }}{{b_{33} }}} ;\,\;k_{3} = \frac{1}{{\kappa_{33} }} $$

Appendix 2

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z1} = \left\{ {\frac{1}{{k_{2}^{2} h}}\left( \begin{gathered} 2\cosh \left( \frac{z}{h} \right)f_{14} h^{3} k_{1} k_{2}^{2} {\varvec{\varXi }}_{s2x} \hfill \\ + \sinh \left( \frac{z}{h} \right)e_{31} h^{4} k_{1} k_{2}^{2} {\varvec{\varXi }}_{s2x} \hfill \\ - k_{2}^{2} \left\{ {k_{3} e_{31} z\left\{ {{\varvec{\varXi }}_{s2x} .\left( {k_{0} + 1} \right) + {\varvec{\varXi }}_{b2x} } \right\}h} \right\} \hfill \\ \end{gathered} \right)} \right\}; $$
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z2} = \frac{{\sinh \left( {\frac{{k_{2} h}}{2}} \right)}}{{k_{2}^{2} b_{33} h\left( {e^{{2k_{2} h}} - 1} \right)}}\left( \begin{gathered} \left( \begin{gathered} - hf_{14} \cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ + 4h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - \left\{ {{\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{s2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ + \left( \begin{gathered} - \varepsilon_{\rm{s}} hf_{14} \cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ + 4h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - \left\{ {{\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{s2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right); $$
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z3} = \frac{{e^{{ - k_{2} z}} }}{{2\left( {e^{{2k_{2} h}} - 1} \right)k_{2} b_{33} }}\left( \begin{gathered} \left( \begin{gathered} 2h\left( {b_{33} e_{31} hk_{1} - \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ + 4h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - 2k_{3} e_{31} \left\{ {{\varvec{\varXi }}_{s2x} .\left( {k_{0} + 1} \right) + {\varvec{\varXi }}_{b2x} } \right\}b_{33} \hfill \\ - \left\{ {{\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{s2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ + 2\left( \begin{gathered} - h\left( {b_{33} e_{31} hk_{1} + \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ + 2h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ + k_{3} e_{31} \left\{ {{\varvec{\varXi }}_{s2x} .\left( {k_{0} + 1} \right) + {\varvec{\varXi }}_{b2x} } \right\}b_{33} \hfill \\ - \frac{1}{2}\left\{ {{\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{s2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right); $$
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z4} = \frac{{f_{14} e^{{k_{2} z}} }}{{2\left( {e^{{2k_{2} h}} - 1} \right)k_{2} b_{33} }}\left( \begin{gathered} \left( \begin{gathered} 2h\left( {b_{33} e_{31} hk_{1} + \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - 4h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - 2k_{3} e_{31} \left\{ {{\varvec{\varXi }}_{s2x} .\left( {k_{0} + 1} \right) + {\varvec{\varXi }}_{b2x} } \right\}b_{33} \hfill \\ + \left\{ {{\varvec{\varXi }}_{s2x} + {\varvec{\varXi }}_{b2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{1}{2}k_{2} h}} \hfill \\ - 2\left( \begin{gathered} h\left( {b_{33} e_{31} hk_{1} - \frac{1}{2}f_{14} } \right)\cosh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ 2h\left( {b_{33} k_{1} + \frac{1}{2}} \right)f_{14} \sinh \left( \frac{1}{2} \right){\varvec{\varXi }}_{s2x} \hfill \\ - k_{3} e_{31} \left\{ {{\varvec{\varXi }}_{s2x} .\left( {k_{0} + 1} \right) + {\varvec{\varXi }}_{b2x} } \right\}b_{33} \hfill \\ - \frac{1}{2}\left\{ {{\varvec{\varXi }}_{s2x} + {\varvec{\varXi }}_{b2x} } \right\}f_{14} h \hfill \\ \end{gathered} \right)e^{{\frac{3}{2}k_{2} h}} \hfill \\ \end{gathered} \right) $$
$$ {\varvec{K}}_{\rm{e}}^{\rm{Beam}} =\int\limits_{\Omega } {\left( {{\varvec{\varXi }}_{b2x}^{\rm T} z^{2} C_{11} {\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{b2x}^{\rm T} zfC_{11} {\varvec{\varXi }}_{s2x} + {\varvec{\varXi }}_{s2x}^{\rm T} zfC_{11} {\varvec{\varXi }}_{b2x} + {\varvec{\varXi }}_{s2x}^{\rm T} f^{2} C_{11} {\varvec{\varXi }}_{s2x} + {\varvec{\varXi }}_{sx}^{\rm T} g_{z} c_{66} {\varvec{\varXi }}_{sx} } \right.} $$
$$ - \left( {z{\varvec{\varXi }}_{b2x} + f(z){\varvec{\varXi }}_{s2x} } \right)^{\rm T} e_{31} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z1} - \left( {z{\varvec{\varXi }}_{b2x} + f(z){\varvec{\varXi }}_{s2x} } \right)^{\rm T} e_{31} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z2} $$
$$ + \left( {z{\varvec{\varXi }}_{b2x} + f(z){\varvec{\varXi }}_{s2x} } \right)^{\rm T} e_{31} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z3} - \left( {z{\varvec{\varXi }}_{b2x} + f(z){\varvec{\varXi }}_{s2x} } \right)^{\rm T} e_{31} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z4} $$
$$ - \left( {{\varvec{\varXi }}_{b2x} + \frac{\partial f(z)}{{\partial z}}{\varvec{\varXi }}_{s2x} } \right)^{\rm T} f_{14} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z1} - \left( {{\varvec{\varXi }}_{b2x} + \frac{\partial f(z)}{{\partial z}}{\varvec{\varXi }}_{s2x} } \right)^{\rm T} f_{14} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z2} $$
$$ + \left( {{\varvec{\varXi }}_{b2x} + \frac{\partial f(z)}{{\partial z}}{\varvec{\varXi }}_{s2x} } \right)^{\rm T} f_{14} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z3} - \left( {{\varvec{\varXi }}_{b2x} + \frac{\partial f(z)}{{\partial z}}{\varvec{\varXi }}_{s2x} } \right)^{\rm T} \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{E}}_{z4} } \right)\text{d}\Omega ; $$
$$ {\varvec{F}}_{\rm{e}}^{\psi } = \frac{1}{2}\int\limits_{\Omega } {\left( {\left( {z{\varvec{H}}_{b2x} + f(z){\varvec{H}}_{s2x} } \right)^{\rm T} e_{31} \left\{ {\frac{\psi }{h}} \right\} + \left( {{\varvec{\varXi }}_{b2x} + \frac{\partial f(z)}{{\partial z}}{\varvec{\varXi }}_{s2x} } \right)^{\rm T} f_{14} \left\{ {\frac{\psi }{h}} \right\}} \right)} \text{d}\Omega $$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luu, G.T., Civalek, Ö. & Van Tuyen, B. The mechanical response of nanobeams considering the flexoelectric phenomenon in the temperature environment. Arch Appl Mech 94, 493–514 (2024). https://doi.org/10.1007/s00419-023-02532-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-023-02532-y

Keywords

Search

Navigation