Skip to main content
SpringerLink
Log in

Dynamical stability of pipe conveying fluid with various lateral distributed loads

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

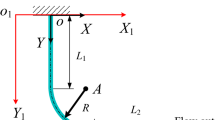
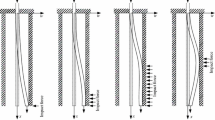
The conveyance of fluid through pipes is a common occurrence in practical applications, and the dynamic stability of such systems has been a subject of interest for many decades. In this paper, we investigate the dynamic stability of a cantilevered pipe conveying fluid, considering the lateral distributed load as a critical factor. To achieve this, we employ the differential quadrature method to solve the eigenvalue equations for various load patterns. Remarkably, we observe excellent agreement with exact solutions and the Argand diagram. By analyzing the relationship between circular frequency and dimensionless velocity, we demonstrate that the descending distributed load pattern exhibits the highest stability. For certain conditions, it is possible to enhance stability. The results obtained in this study provide valuable insights for improving the stability of cantilevered pipe conveying fluid through a different approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Paidoussis, M.P.: Fluid Structure Interactions: Slender Structures and Axial Flow, vol. 2. Academic Press, London (2016)

    Google Scholar 

  2. Ibrahim, R.A.: Overview of mechanics of pipes conveying fluids-part I: fundamental studies. J. Press. Vessel Technol. 132(3), 034001 (2010)

    Article  Google Scholar 

  3. Zeng, L., Lv, T., Chen, H., Ma, T., Fang, Z., Shi, J.: Flow accelerated corrosion of X65 steel gradual contraction pipe in high CO2 partial pressure environments. Arab. J. Chem. 16(8), 104935 (2023)

    Article  Google Scholar 

  4. Xia, Y., Shi, M., Zhang, C., Wang, C., Sang, X., Liu, R., Zhao, P., An, G., Fang, H.: Analysis of flexural failure mechanism of ultraviolet cured-in-place-pipe materials for buried pipelines rehabilitation based on curing temperature monitoring. Eng. Fail. Anal. 142, 106763 (2022)

    Article  Google Scholar 

  5. Wang, Y., Lou, M., Wang, Y., Wu, W., Yang, F.: Stochastic failure analysis of reinforced thermoplastic pipes under axial loading and internal pressure. China Ocean Eng. 36, 614–628 (2022)

    Article  Google Scholar 

  6. Wang, Y., Lou, M., Wang, Y., Fan, C., Tian, C., Qi, X.: Experimental investigation of the effect of rotation rate and current speed on the dynamic response of riserless rotating drill string. Ocean Eng. 280, 114542 (2023)

    Article  Google Scholar 

  7. Sazesh, S., Shams, S.: Vibration analysis of cantilever pipe conveying fluid under distributed random excitation. J. Fluids Struct. 87, 84–101 (2019)

    Article  Google Scholar 

  8. Paidoussis, M.P., Li, G.X.: Pipes conveying fluid: a model dynamical problem. J. Fluids Struct. 7(2), 137–204 (1993)

    Article  Google Scholar 

  9. Zhou, K., Dai, H.L., Wang, L., Ni, Q., Hagedorm, P.: Modeling and nonlinear dynamics of cantilevered pipe with tapered free end concurrently subjected to axial internal and external flows. Mech. Syst. Signal Process. 169, 108794 (2022)

    Article  Google Scholar 

  10. Tang, Y., Zhen, Y., Fang, B.: Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Appl. Math. Model. 56, 123–136 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  11. El-Sayed, T.A., El-Mongy, H.H.: Free vibration and stability analysis of a multi-span pipe conveying fluid using exact and variational iteration methods combined with transfer matrix method. Appl. Math. Model. 71, 173–193 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  12. Oyelade, A.O., Oyediran, A.A.: The effect of various boundary conditions on the nonlinear dynamics of slightly curved pipes under thermal loading. Appl. Math. Model. 87, 332–350 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Ni, Q., Zhang, Z.L., Wang, L.: Application of the differential transformation method to vibration analysis of pipes conveying fluid. Appl. Math. Comput. 217, 7028–7038 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Wang, L., Jiang, T.L., Dai, H.L., Ni, Q.: Three-dimensional vortex-induced vibrations of supported pipes conveying fluid based on wake oscillator models. J. Sound Vib. 422, 590–612 (2018)

    Article  Google Scholar 

  15. Ding, H., Ji, J., Chen, L.: Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mech. Syst. Signal Process. 121, 675–688 (2019)

    Article  Google Scholar 

  16. Yoon, H., Son, I.S.: Dynamic response of rotating flexible cantilever pipe conveying fluid with tip mass. Int. J. Mech. Sci. 49, 878–887 (2007)

    Article  Google Scholar 

  17. Zhou, K., Xiong, F.R., Jiang, N.B., et al.: Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink. Nonlinear Dyn. 95, 1435–1456 (2019)

    Article  Google Scholar 

  18. Ghayesh, M.H., Paidoussis, M.P., Modarres-Sadeghi, Y.: Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring-support and an end-mass. J. Sound Vib. 330, 2869–2899 (2011)

    Article  Google Scholar 

  19. Paidoussis, M.P., Li, G.X., Moon, F.C.: Chaotic oscillations of the autonomous system of a constrained pipe conveying fluid. J. Sound Vib. 135(1), 1–19 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  20. Paidoussis, M.P., Semler, C.: Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: a full nonlinear analysis. Nonlinear Dyn. 4, 655–670 (1993)

    Article  Google Scholar 

  21. Ni, Q., Wang, Y., Tang, M., et al.: Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints. Nonlinear Dyn. 81, 893–906 (2015)

    Article  Google Scholar 

  22. Liu, Z.Y., Wang, L., Dai, H.L., et al.: Nonplanar vortex-induced vibrations of cantilevered pipes conveying fluid subjected to loose constraints. Ocean Eng. 178, 1–19 (2019)

    Article  Google Scholar 

  23. Wang, Y., Tang, M., Yang, M., et al.: Three-dimensional dynamics of a cantilevered pipe conveying pulsating fluid. Appl. Math. Model. 114, 502–524 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhou, J., Chang, X., Xiong, Z., Li, Y.: Stability and nonlinear vibration analysis of fluid-conveying composite pipes with elastic boundary conditions. Thin-Walled Struct. 179, 109597 (2022)

    Article  Google Scholar 

  25. Dai, H.L., Wang, L., Ni, Q.: Dynamics of a fluid-conveying pipe composed of two different materials. Int. J. Eng. Sci. 73, 67–75 (2013)

    Article  Google Scholar 

  26. Bahaadini, R., Dashtbayazi, M.R., Hosseini, M., Parizi, Z.K.: Stability analysis of composite thin-walled pipes conveying fluid. Ocean Eng. 160, 311–323 (2018)

    Article  Google Scholar 

  27. ElNajjar, J., Daneshmand, F.: Stability of horizontal and vertical pipes conveying fluid under the effects of additional point masses and springs. Ocean Eng. 206, 106943 (2020)

    Article  Google Scholar 

  28. Jiang, T., Dai, H., Wang, L.: Three-dimensional dynamics of fluid-conveying pipe simultaneously subjected to external axial flow. Ocean Eng. 217, 107970 (2020)

    Article  Google Scholar 

  29. Abdelbaki, A.R., Paidoussis, M.P., Misra, A.K.: A nonlinear model for a hanging tubular cantilever simultaneously subjected to internal and confined external axial flows. J. Sound Vib. 449, 349–367 (2019)

    Article  Google Scholar 

  30. Bonanos, A.M., Georgiou, M.C., Stokos, K.G., Papanicolas, C.N.: Engineering aspects and thermal performance of molten salt transfer lines in solar power applications. Appl. Therm. Eng. 154, 294–301 (2019)

    Article  Google Scholar 

  31. Zhang, M., Xie, Y., Wang, Z.: An air heat tracing system of firefighting pipeline in cold region highway tunnel. Sustainability 14, 16056 (2022)

    Article  Google Scholar 

  32. Wang, X., Wang, Y.: Free vibration analysis of multiple-stepped beams by the differential quadrature element method. Appl. Math. Comput. 219, 5802–5810 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Charles, W.B., Moinuddin, M.: Differential quadrature method in computational mechanics: a review. Appl. Mech. Rev. 49(1), 1–28 (1996)

    Article  Google Scholar 

  34. Xu, J., Wang, L.: Dynamics and Control of Fluid-Conveying Pipe Systems. Science Press, Beijing (2015)

    Google Scholar 

  35. Liu, Y., Chen, L., Chen, W.: Mechanics of Vibrations, 3rd edn. Higher Education Press, Beijing (2019)

    Google Scholar 

  36. Thomson, W.T.: Theory of Vibration with Applications. Unwin Hyman Ltd., London (1988)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Nuclear Power Institute of China, Chengdu, 610213, Sichuan, China

    Yu Zhang & Pengzhou Li

Authors
  1. Yu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pengzhou Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Li, P. Dynamical stability of pipe conveying fluid with various lateral distributed loads. Arch Appl Mech 93, 4093–4106 (2023). https://doi.org/10.1007/s00419-023-02481-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-023-02481-6

Keywords

Search

Navigation