Skip to main content
SpringerLink
Log in

Double porous thermoelastic waves in a homogeneous, isotropic solid with inviscid liquid

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

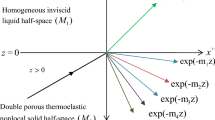
A two-dimensional model based on Lord–Shulman’s thermoelasticity theory has been constructed to examine the impact of various physical parameters of the medium in a double porous thermoelastic, isotropic, homogeneous half-space in contact with an inviscid liquid half-space. It has been discovered that four coupled longitudinal waves and one uncoupled transverse wave may exist in the solid medium and one mechanical wave in the liquid medium, all propagating at different speeds. It has been observed that linked longitudinal waves exhibit dispersion, attenuation, etc., and depend on both kinds of voids and the thermal characteristics of the medium. The simplest form of the complex secular equation has been derived. The amplitudes of solid and liquid displacements, volume fractional fields, and temperature change at the interface have also been obtained. The computer-simulated results for magnesium crystal material for different wave profiles have been graphically displayed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Lord, H.W., Shulman, Y.: A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15(5), 299–309 (1967). https://doi.org/10.1016/0022-5096(67)90024-5

    Article  MATH  Google Scholar 

  2. Aifantis, E.C.: Introducing a multi-porous medium. Dev. Mech 8(3), 209–211 (1977)

    Google Scholar 

  3. Nunziato, J.W., Cowin, S.C.: A nonlinear theory of elastic materials with voids. Arch. Ration. Mech. Anal. 72(2), 175–201 (1979). https://doi.org/10.1007/BF00249363

    Article  MathSciNet  MATH  Google Scholar 

  4. Beskos, D.E., Aifantis, E.C.: On the theory of consolidation with double porosity—II. Int. J. Eng. Sci. 24(11), 1697–1716 (1986). https://doi.org/10.1016/0020-7225(86)90076-5

    Article  MathSciNet  MATH  Google Scholar 

  5. Ieşan, D.: A theory of thermoelastic materials with voids. Acta Mech. 60(1), 67–89 (1986). https://doi.org/10.1007/BF01302942

    Article  MathSciNet  Google Scholar 

  6. Dhaliwal, R.S., Wang, J.: A heat-flux dependent theory of thermoelasticity with voids. Acta Mech. 110(1), 33–39 (1995). https://doi.org/10.1007/BF01215413

    Article  MathSciNet  MATH  Google Scholar 

  7. Khalili, N.: Coupling effects in double porosity media with deformable matrix. Geophys. Res. Lett. 30(22), 10–12 (2003). https://doi.org/10.1029/2003GL018544

    Article  Google Scholar 

  8. Khalili, N., Selvadurai, A.P.S.: A fully coupled constitutive model for thermo-hydro-mechanical analysis in elastic media with double porosity. Geophys. Res. Lett. (2003). https://doi.org/10.1029/2003GL018838

    Article  Google Scholar 

  9. Singh, J., Tomar, S.K.: Plane waves in thermo-elastic material with voids. Mech. Mater. 39(10), 932–940 (2007)

    Article  Google Scholar 

  10. Straughan, B.: Stability and uniqueness in double porosity elasticity. Int. J. Eng. Sci. 65, 1–8 (2013). https://doi.org/10.1016/j.ijengsci.2013.01.001

    Article  MathSciNet  MATH  Google Scholar 

  11. Ieşan, D., Quintanilla, R.: On a theory of thermoelastic materials with a double porosity structure. J. Therm. Stress. 37(9), 1017–1036 (2014). https://doi.org/10.1080/01495739.2014.914776

    Article  Google Scholar 

  12. Scarpetta, E., Svanadze, M., Zampoli, V.: Fundamental solutions in the theory of thermoelasticity for solids with double porosity. J. Therm. Stress. 37(6), 727–748 (2014). https://doi.org/10.1080/01495739.2014.885337

    Article  Google Scholar 

  13. Svanadze, M.: Steady vibration problems in the theory of elasticity for materials with double voids. Acta Mech. 229(4), 1517–1536 (2018). https://doi.org/10.1007/s00707-017-2077-z

    Article  MathSciNet  MATH  Google Scholar 

  14. Gales, C., Chirita, S.: Wave propagation in materials with double porosity. Mech Mater. 149, 1–9 (2020)

    Article  Google Scholar 

  15. Plona, T.J., Behravesh, M., Mayer, W.G.: Rayleigh and Lamb waves at liquid-solid boundaries. Ultrasonics 2(2), 171–175 (1975)

    Article  Google Scholar 

  16. Mozhaev, V.G., Weihnacht, M.: Subsonic leaky Rayleigh waves at liquid-solid interfaces. Ultrasonics 40(1–8), 927–933 (2002). https://doi.org/10.1016/S0041-624X(02)00233-0

    Article  Google Scholar 

  17. Sharma, J.N., Pathania, V.: Generalized thermoelastic Lamb waves in a plate bordered with layers of inviscid liquid. J. Sound Vib. 268(5), 897–916 (2003). https://doi.org/10.1016/S0022-460X(02)01639-5

    Article  MATH  Google Scholar 

  18. Barak, M.S., Kumari, M., Kumar, M.: Effect of local fluid flow on the propagation of plane waves at an interface of water/double-porosity solid with underlying uniform elastic solid. Ocean Eng. 147, 195–205 (2018). https://doi.org/10.1016/j.oceaneng.2017.10.030

    Article  Google Scholar 

  19. Pathania, V., Joshi, P.: Waves in thermoelastic solid half-space containing voids with liquid loadings. ZAMM - J. Appl. Math. Mech. Zeitschrift für Angew. Math. und Mech. 101(12), e202100093 (2021). https://doi.org/10.1002/zamm.202100093

    Article  MathSciNet  Google Scholar 

  20. Pathania, V., Dhiman, P.: On lamb-type waves in a poro-thermoelastic plate immersed in the inviscid fluid. Waves Random Complex Media (2021). https://doi.org/10.1080/17455030.2021.2014599

    Article  Google Scholar 

  21. Kumar, M., Liu, X., Kalkal, K.K., Dalal, V., Kumari, M.: Inhomogeneous wave reflection from the surface of a partially saturated thermoelastic porous media. Int. J. Numer. Methods Heat Fluid Flow 32(6), 1911–1943 (2022). https://doi.org/10.1108/HFF-04-2021-0279

    Article  Google Scholar 

  22. Kumari, M., Kumar, M.: Wave-induced flow of pore fluid in a cracked porous solid containing penny-shaped inclusions. Pet. Sci. 18(5), 1390–1408 (2021). https://doi.org/10.1016/j.petsci.2021.09.022

    Article  Google Scholar 

  23. Kumar, M., Liu, X., Kumari, M., Yadav, P.: Wave propagation at the welded interface of an elastic solid and unsaturated poro-thermoelastic solid. Int. J. Numer. Methods Heat Fluid Flow 32(11), 3526–3550 (2022). https://doi.org/10.1108/HFF-01-2022-0008

    Article  Google Scholar 

  24. Kumari, M., Kumar, M.: Reflection of inhomogeneous waves at the surface of a cracked porous solid with penny-shaped inclusions. Waves Random Complex Media 32(4), 1992–2013 (2022). https://doi.org/10.1080/17455030.2020.1842555

    Article  MathSciNet  MATH  Google Scholar 

  25. Kumari, M., Kaswan, P., Kumar, M., Yadav, P.: Reflection of inhomogeneous plane waves at the surface of an unsaturated porothermoelastic media. Eur. Phys. J. Plus 137(6), 729 (2022). https://doi.org/10.1140/epjp/s13360-022-02880-8

    Article  Google Scholar 

  26. Achenbach, J.D.: Wave propagation in elastic solids. Elsevier, Amsterdam (1975). https://doi.org/10.1016/C2009-0-08707-8

    Book  MATH  Google Scholar 

  27. Sharma, J.N., Pathania, V.: Propagation of leaky surface waves in thermoelastic solids due to inviscid fluid loadings. J. Therm. Stress. 28(5), 485–519 (2005). https://doi.org/10.1080/01495730590925010

    Article  Google Scholar 

  28. Singh, D., Kumar, D., Tomar, S.K.: Plane harmonic waves in a thermoelastic solid with double porosity. Math. Mech. Solids 25(4), 869–886 (2020). https://doi.org/10.1177/1081286519890053

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The third author is thankful to the Council of Scientific and Industrial Research (CSIR), New Delhi, India (File no. 09/1293(0003)/2019-EMR-I), for providing the junior research fellowship (JRF).

The authors declare that they have no conflict of interest.

Author information

Authors and Affiliations

  1. Department of Mathematics, Himachal Pradesh University Regional Centre, Dharamshala, HP, India

    Vijayata Pathania

  2. Department of Mathematics, Indira Gandhi University, Meerpur, Rewari, HR, India

    Rajesh Kumar, Vipin Gupta & M. S. Barak

Authors
  1. Vijayata Pathania
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vipin Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. S. Barak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. S. Barak.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$ L_{1} = 1 + \tau_{0} (1 + \varepsilon ) + \frac{1}{{(a_{8} - a_{3} )}}\left\{ {\left( {\frac{1}{{\delta_{2}^{2} }} + \frac{{a_{8} }}{{\delta_{1}^{2} }}} \right) + \frac{1}{{\omega^{2} }}\left( {a_{6} - a_{11} + a_{2} a_{9} - a_{2} a_{4} + a_{3} a_{10} - a_{5} a_{8} + a_{1} a_{4} a_{8} - a_{1} a_{3} a_{9} } \right)} \right\} $$
$$ \begin{aligned} L_{2} = & \tau _{0} + \frac{1}{{(a_{8} - a_{3} )}}\left[\frac{1}{{\delta _{1}^{2} \delta _{2}^{2}}} + \left( {\frac{1}{{\delta _{2}^{2} }} + \frac{{a_{8} }}{{\delta _{1}^{1} }}} \right)\left\{ 1 + \tau _{0} (1 + \varepsilon )\right\} + \frac{1}{{\omega ^{2} }}\left\{ a_{6} - a_{{11}} + a_{3} a_{{10}} - a_{5} a_{8} + \frac{1}{{\delta _{1}^{2} }}(a_{2} a_{9} - a_{{11}} ) \right.\right.\\ & \quad + \frac{1}{{\delta _{2}^{2} }}(a_{1} a_{4} - a_{5} ) + \tau _{0} (a_{6} - a_{{11}} + a_{2} a_{9} - a_{2} a_{4} + a_{3} a_{{10}} - a_{5} a_{8} + a_{7} a_{{14}} - a_{4} a_{{14}} + a_{9} a_{{14}} - a_{{12}} a_{{14}} \\ & \quad + a_{4} a_{8} a_{{13}} - a_{1} a_{3} a_{9} + a_{1} a_{4} a_{8} - a_{3} a_{9} a_{{13}} + a_{3} a_{{12}} a_{{13}} - a_{7} a_{8} a_{{13}} + \varepsilon (a_{6} - a_{{11}} + a_{2} a_{{12}} - a_{2} a_{7} + a_{3} a_{{10}} \\ &\left. \left. \quad -\; a_{5} a_{8} + a_{1} a_{3} a_{{12}} + a_{1} a_{7} a_{8} ))\vphantom{\left\{ a_{6} - a_{{11}} + a_{3} a_{{10}} - a_{5} a_{8} + \frac{1}{{\delta _{1}^{2} }}(a_{2} a_{9} - a_{{11}} ) \right.}\right\} + \frac{1}{{\omega ^{4} }}(a_{5} a_{{11}} - a_{6} a_{{10}} + a_{1} a_{6} a_{9} - a_{1} a_{4} a_{{11}} + a_{2} a_{4} a_{{10}} - a_{2} a_{5} a_{9} )\right] \\ \end{aligned} $$
$$\begin{aligned} L_{3} & = \frac{1}{{(a_{8} - a_{3} )}}\left[\frac{1}{{\delta _{1}^{2} \delta _{2}^{2} }}\{ 1 + \tau _{0} (1 + \varepsilon )\} + \tau _{0} \left( {\frac{1}{{\delta _{2}^{2} }} + \frac{{a_{8} }}{{\delta _{1}^{2} }}} \right) - \frac{1}{{\omega ^{2} }}\left\{ \frac{{a_{{11}} }}{{\delta _{1}^{2} }} + \frac{{a_{5} }}{{\delta _{2}^{2} }} - \tau _{0} \left\{ a_{6} - a_{{11}} + a_{3} a_{{10}} - a_{5} a_{8} \right.\right.\right. \\ & \quad + a_{7} a_{{14}} - a_{{12}} a_{{14}} + a_{3} a_{{12}} a_{{13}} - a_{7} a_{8} a_{{13}} - \frac{1}{{\delta _{1}^{2} }}(a_{{11}} - a_{2} a_{9} + a_{{12}} a_{{14}} - a_{9} a_{{14}} ) - \frac{1}{{\delta _{2}^{2} }}(a_{5} - a_{1} a_{4} + a_{7} a_{{13}} \\ &\left.\left. \quad -\; a_{4} a_{{13}} ) - \varepsilon \left\{ \frac{1}{{\delta _{1}^{2} }}(a_{{11}} - a_{2} a_{{12}} ) + \frac{1}{{\delta _{2}^{2} }}(a_{5} - a_{1} a_{7} )\right\} \right\} \right\} - \frac{1}{{\omega ^{4} }}\{ a_{6} a_{{10}} - a_{5} a_{{11}} + \tau _{0} \{ a_{6} a_{{10}} - a_{1} a_{6} a_{9} \\ & \quad + a_{1} a_{4} a_{{11}} - a_{2} a_{4} a_{{10}} + a_{2} a_{5} a_{9} - a_{4} a_{{10}} a_{{14}} + a_{4} a_{{11}} a_{{13}} - a_{6} a_{9} a_{{13}} + a_{5} a_{9} .a_{{14}} - a_{5} a_{{12}} a_{{14}} + a_{6} a_{{12}} a_{{13}} \\ & \quad - a_{7} a_{{11}} a_{{13}} + a_{7} a_{{10}} a_{{14}} - a_{1} a_{7} a_{9} a_{{14}} + a_{1} a_{4} a_{{12}} a_{{14}} - a_{2} a_{4} a_{{12}} a_{{13}} + a_{2} a_{7} a_{9} a_{{13}} - \varepsilon (a_{5} a_{{11}} - a_{6} a_{{10}} \\ & \left. \quad +\; a_{1} a_{6} a_{{12}} - a_{1} a_{7} a_{{11}} + a_{2} a_{7} a_{{10}} - a_{2} a_{5} a_{{12}} )\} \}\right] \\ \end{aligned} $$
$$ \begin{aligned} L_{4} & \quad = \frac{{\tau_{0} }}{{a_{8} - a_{3} }}[\frac{1}{{\delta_{1}^{2} \delta_{2}^{2} }} - \frac{1}{{\omega^{2} }}\left\{ {\frac{1}{{\delta_{1}^{2} }}(a_{11} + a_{12} a_{14} ) + \frac{1}{{\delta_{2}^{2} }}(a_{5} + a_{7} a_{13} )} \right\} + \frac{1}{{\omega^{4} }}(a_{5} a_{11} - a_{6} a_{10} + a_{5} a_{12} a_{14} \\ & \quad \;- a_{6} .a_{12} a_{13} + a_{7} a_{11} a_{13} - a_{7} a_{10} a_{14} )] \\ \end{aligned} $$

Appendix B

$$ \begin{aligned} V_{q} & \quad = ((a_{3} a_{9} - a_{4} a_{8} - a_{3} a_{12} + a_{7} a_{8} )m_{q}^{4} + (a_{6} a_{12} - a_{6} a_{9} - a_{2} a_{4} a_{12} + a_{2} a_{7} a_{9} + \Gamma_{3}^{2} a_{4} a_{8} + \Gamma_{1}^{2} a_{3} a_{12} - \Gamma_{1}^{2} a_{7} a_{8} \\ & \quad - \Gamma_{3}^{2} a_{7} a_{8} - 2a_{3} a_{9} k^{2} + a_{4} a_{8} k^{2} + a_{3} a_{12} k^{2} )m_{q}^{2} + a_{3} a_{9} k^{4} - \Gamma_{1}^{2} a_{6} a_{12} + a_{6} a_{9} k^{2} + a_{2} a_{4} a_{12} k^{2} - a_{2} a_{7} a_{9} k^{2} \\ & \quad + \Gamma_{1}^{2} \Gamma_{3}^{2} a_{7} a_{8} - \Gamma_{3}^{2} a_{4} a_{8} k^{2} - \Gamma_{1}^{2} a_{3} a_{12} k^{2} )/\sigma^{*} \\ \end{aligned} $$
$$ \begin{aligned} W_{q} & = ((a_{4} - a_{7} + a_{12} - a_{9} )m_{q}^{4} + (a_{7} a_{10} - a_{4} a_{10} + \Gamma_{1}^{2} a_{7} - \Gamma_{1}^{2} a_{12} + \Gamma_{2}^{2} a_{9} - \Gamma_{2}^{2} a_{12} + a_{7} k^{2} - 2a_{4} k^{2} + a_{9} k^{2} - a_{1} a_{7} a_{9} \\ & \quad + a_{1} a_{4} a_{12} )m_{q}^{2} + a_{4} k^{4} - \Gamma_{1}^{2} a_{7} k^{2} + \Gamma_{1}^{2} \Gamma_{2}^{2} a_{12} - \Gamma_{2}^{2} a_{9} k^{2} + a_{4} a_{10} k^{2} - \Gamma_{1}^{2} a_{7} a_{10} + a_{1} a_{7} a_{9} k^{2} - a_{1} a_{4} a_{12} k^{2} )/\sigma^{*} \\ \end{aligned} $$
$$ \begin{aligned} S_{q} & = ((a_{8} - a_{3} )m_{q}^{6} + (a_{6} - a_{2} a_{4} + a_{2} a_{9} + a_{3} a_{10} + \Gamma_{1}^{2} a_{3} - \Gamma_{1}^{2} a_{8} - \Gamma_{2}^{2} a_{8} - \Gamma_{3}^{2} a_{8} + 2a_{3} k^{2} - a_{1} a_{3} a_{9} \\ & \quad + a_{1} a_{4} a_{8} )m_{q}^{4} + (\Gamma_{1}^{2} \Gamma_{2}^{2} a_{8} - \Gamma_{1}^{2} a_{6} - a_{3} k^{4} - a_{6} k^{2} - a_{6} a_{10} + \Gamma_{1}^{2} \Gamma_{3}^{2} a_{8} + \Gamma_{2}^{2} \Gamma_{3}^{2} a_{8} - 2\Gamma_{1}^{2} a_{3} k^{2} \\ & \quad + a_{1} a_{6} a_{9} + a_{2} a_{4} a_{10} - \Gamma_{2}^{2} a_{2} a_{9} - \Gamma_{1}^{2} a_{3} a_{10} + 2a_{2} a_{4} k^{2} - a_{2} a_{9} k^{2} - a_{3} a_{10} k^{2} - \Gamma_{3}^{2} a_{1} a_{4} a_{8} + 2a_{1} a_{3} a_{9} k^{2} \\ & \quad - a_{1} a_{4} a_{8} k^{2} )m_{q}^{2} + \Gamma_{1}^{2} a_{3} k^{4} + \Gamma_{1}^{2} a_{6} k^{2} + \Gamma_{1}^{2} a_{6} a_{10} - a_{2} a_{4} k^{4} - a_{1} \cdot a_{3} a_{9} k^{4} - a_{1} a_{6} a_{9} k^{2} - a_{2} a_{4} a_{10} k^{2} \\ & \quad + \Gamma_{2}^{2} a_{2} a_{9} k^{2} + \Gamma_{1}^{2} a_{3} a_{10} k^{2} - \Gamma_{1}^{2} \Gamma_{2}^{2} \Gamma_{3}^{2} a_{8} + \Gamma_{3}^{2} a_{1} a_{4} a_{8} \cdot k^{2} )/\sigma^{*} \\ \end{aligned} $$
$$ \begin{aligned} \sigma^{*} & = (a_{3} - a_{8} )m_{q}^{4} + (a_{8} \Gamma_{2}^{2} - 2a_{3} k^{2} + a_{8} \Gamma_{3}^{2} - a_{6} + a_{2} a_{7} - a_{3} a_{10} + a_{1} a_{3} a_{12} - a_{2} a_{12} - a_{1} a_{7} a_{8} )m_{q}^{2} + a_{6} a_{10} \\ & \quad - \Gamma_{2}^{2} \Gamma_{3}^{2} a_{8} + a_{3} k^{4} - a_{1} a_{6} a_{12} + a_{6} k^{2} - a_{2} a_{7} a_{10} + \Gamma_{2}^{2} a_{2} a_{12} - a_{2} a_{7} k^{2} + a_{3} a_{10} k^{2} - a_{1} a_{3} a_{12} k^{2} + \Gamma_{3}^{2} a_{1} a_{7} a_{8} \\ \end{aligned} $$

Appendix C

$$ \begin{aligned} U_{2} /U_{1} & = ((V_{3} W_{1} - V_{1} W_{3} )m_{1} m_{3} m_{6} + (V_{1} W_{4} - V_{4} W_{1} )m_{1} m_{4} m_{6} + (V_{4} W_{3} - V_{3} W_{4} )m_{3} m_{4} m_{6} + (V_{1} W_{3} - V_{3} W_{1} + V_{4} W_{1} \\ & \quad + V_{4} W_{1} - V_{1} W_{4} + V_{3} W_{4} - V_{4} W_{3} + p_{1} \iota k(V_{1} W_{3} - V_{3} W_{1} + V_{4} W_{1} - V_{1} W_{4} + V_{3} W_{4} - V_{4} W_{3} ))p_{2} m_{1} m_{3} m_{4} \\ & \quad + (V_{3} W_{1} - V_{1} W_{3} + V_{1} W_{4} - V_{4} W_{1} + V_{4} W_{3} - V_{3} W_{4} )p_{1}^{2} m_{1} m_{2} m_{4} m_{5} m_{6} )/\sigma^{**} \\ \end{aligned} $$
$$ \begin{aligned} U_{3} /U_{1} & = ((V_{1} W_{2} - V_{2} W_{1} )m_{1} m_{2} m_{6} + (V_{4} W_{1} - V_{1} W_{4} )m_{1} m_{4} m_{6} + (V_{2} W_{4} - V_{4} W_{2} )m_{2} m_{4} m_{6} + (V_{2} W_{1} - V_{1} W_{2} \\ & \quad + V_{1} W_{4} - V_{4} W_{1} + V_{4} W_{2} - V_{2} W_{4} + p_{1} \iota k(V_{2} W_{1} - V_{1} W_{2} + V_{1} W_{4} - V_{4} W_{1} + V_{4} W_{2} - V_{2} W_{4} ))p_{2} m_{1} m_{2} m_{4} \\ & \quad + (V_{1} W_{2} - V_{2} W_{1} + V_{4} W_{1} - V_{1} W_{4} + V_{2} W_{4} - V_{4} W_{2} )p_{1}^{2} m_{1} m_{2} m_{4} m_{5} m_{6} )/\sigma^{**} \\ \end{aligned} $$
$$ \begin{aligned} U_{4} /U_{1} & = ((V_{2} W_{1} - V_{1} W_{2} )m_{1} m_{2} m_{6} + (V_{1} W_{3} - V_{3} W_{1} )m_{1} m_{3} m_{6} + (V_{3} W_{2} - V_{2} W_{3} )m_{2} m_{3} m_{6} + (V_{1} W_{2} - V_{2} W_{1} \\ & \quad + V_{3} W_{1} - V_{1} W_{3} + V_{2} W_{3} - V_{3} W_{2} + p_{1} \iota k(V_{1} W_{2} - V_{2} W_{1} + V_{3} W_{1} - V_{1} W_{3} + V_{2} W_{3} - V_{3} W_{2} ))p_{2} m_{1} m_{2} m_{3} \\ & \quad + (V_{2} W_{1} - V_{1} W_{2} + V_{1} W_{3} - V_{3} W_{1} + V_{3} W_{2} - V_{2} W_{3} )p_{1}^{2} m_{1} m_{2} m_{3} m_{5} m_{6} )/\sigma^{**} \\ \end{aligned} $$
$$ \begin{gathered} U_{5} /U_{1} = p_{1} m_{6} ((V_{1} W_{2} - V_{2} W_{1} + V_{3} W_{1} - V_{1} W_{3} + V_{2} W_{3} - V_{3} W_{2} )m_{1} m_{2} m_{3} + (V_{2} W_{1} - V_{1} W_{2} + V_{1} W_{4} - V_{4} W_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + V_{4} W_{2} - V_{2} W_{4} )m_{1} m_{2} m_{4} + (V_{1} W_{3} - V_{3} W_{1} + V_{4} W_{1} - V_{1} W_{4} + V_{3} W_{4} - V_{4} W_{3} )m_{1} m_{3} m_{4} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + (V_{3} W_{2} - V_{2} W_{3} + V_{2} W_{4} - V_{4} W_{2} + V_{3} W_{4} + V_{4} W_{3} ))/\sigma^{**} \hfill \\ \end{gathered} $$
$$ \begin{aligned} U_{6} /U_{1} & = (p_{1} \iota k + 1)((V_{2} W_{1} - V_{1} W_{2} + V_{1} W_{3} - V_{3} W_{1} + V_{3} W_{2} - V_{2} W_{3} )m_{1} m_{2} m_{3} + (V_{1} W_{2} - V_{2} W_{1} + V_{4} W_{1} - V_{1} W_{4} \\ & \quad + V_{2} W_{4} - V_{4} W_{2} )m_{1} m_{2} m_{4} + (V_{3} W_{1} - V_{1} W_{3} + V_{1} W_{4} - V_{4} W_{1} + V_{4} W_{3} - V_{3} W_{4} )m_{1} m_{3} m_{4} \\ & \quad + (V_{2} W_{3} - V_{3} W_{2} + V_{4} W_{2} - V_{2} W_{4} - V_{3} W_{4} - V_{4} W_{3} ))/\sigma^{**} \\ \end{aligned} $$
$$ \begin{gathered} \sigma^{**} = (V_{2} W_{3} - V_{3} W_{2} )m_{2} m_{3} m_{6} + (V_{4} W_{2} - V_{2} W_{4} )m_{2} m_{4} m_{6} + (V_{3} W_{4} - V_{4} W_{3} )m_{3} m_{4} m_{6} + (V_{3} W_{2} - V_{2} W_{3} + V_{2} W_{4} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - V_{4} W_{2} + V_{3} W_{4} - V_{4} W_{3} + p_{1} \iota k(V_{3} W_{2} - V_{2} W_{3} + V_{2} W_{4} - V_{4} W_{2} + V_{4} W_{3} - V_{3} W_{4} ))p_{2} m_{2} m_{3} m_{4} \,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + (V_{2} W_{3} - V_{3} .W_{2} + V_{4} W_{2} - V_{2} W_{4} + V_{3} W_{4} - V_{4} W_{3} )p_{1}^{2} m_{1} m_{2} m_{3} m_{5} m_{6} \hfill \\ \end{gathered} $$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pathania, V., Kumar, R., Gupta, V. et al. Double porous thermoelastic waves in a homogeneous, isotropic solid with inviscid liquid. Arch Appl Mech 93, 1943–1962 (2023). https://doi.org/10.1007/s00419-023-02364-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-023-02364-w

Keywords

Search

Navigation