Skip to main content
SpringerLink
Log in

Thermal effect on the transient waves in piezoelectric half-space subjected to dynamic loading

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

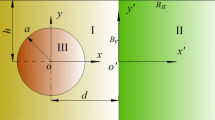
Propagation of transient waves in the piezoelectric half-space under anti-plane dynamic force and in-plane electrical displacement loading is studied theoretically when thermal effect considered. One-sided and two-sided Laplace transforms are firstly employed in obtaining the solutions of mechanical displacement, electrical potential, shear stress and electrical displacement in Laplace space. Cagniard-de Hoop method is then adopted for inverse Laplace transform in determining the analytical transient solutions in time domain. Transient response of the mechanical displacement, shear stress, electric potential and displacement are finally evaluated numerically, and the effect of thermal stress on the transient waves propagating in the piezoelectric half-space is discussed in details. Furthermore, two different electro-mechanic boundary conditions are considered for the propagation of transient waves in the piezoelectric half-space.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Sahu, S.A., Mondal, S., Dewangan, N.: Polarized shear waves in functionally graded piezoelectric material layer sandwiched between corrugated piezomagnetic layer and elastic substrate. J. Sandw. Struct. Mater. 21(8), 2921–2948 (2019)

    Article  Google Scholar 

  2. Kohler, B., et al.: A mode-switchable guided elastic wave transducer. J. Nondestruct. Eval. 39(2), 45 (2020)

    Article  Google Scholar 

  3. Zima, B.: Damage detection in plates based on Lamb wavefront shape reconstruction. Measurement 177, 109206 (2021)

    Article  Google Scholar 

  4. Sahu, S.A., et al.: Characterization of polarized shear waves in FGPM composite structure with imperfect boundary: WKB method. Int. J. Appl. Mech. 11(9), 21 (2019)

    Article  Google Scholar 

  5. Li, M., et al.: Study on the propagation characteristics of SH wave in piemagnetic piezoeletric structures. Mater. Res. Express 6(10), 105707 (2019)

    Article  Google Scholar 

  6. Tian, R., et al.: On Rayleigh waves in a piezoelectric semiconductor thin film over an elastic half-space. Int. J. Mech. Sci. 204, 106565 (2021)

    Article  Google Scholar 

  7. Cao, X., et al.: Generalized Rayleigh surface waves in a piezoelectric semiconductor half space. Meccanica 54(1–2), 271–281 (2019)

    Article  MathSciNet  Google Scholar 

  8. Tian, R., et al.: Some characteristics of elastic waves in a piezoelectric semiconductor plate. J. Appl. Phys. 126(12), 125701 (2019)

    Article  Google Scholar 

  9. Jiao, F., et al.: The dispersion and attenuation of the multi-physical fields coupled waves in a piezoelectric semiconductor. Ultrasonics 92, 68–78 (2019)

    Article  Google Scholar 

  10. Wang, G., et al.: Magnetically induced redistribution of mobile charges in bending of composite beams with piezoelectric semiconductor and piezomagnetic layers. Arch. Appl. Mech. 91(7), 2949–2956 (2021)

    Article  MathSciNet  Google Scholar 

  11. Li, P., Jin, F.: Bleustein-Gulyaev waves in a transversely isotropic piezoelectric layered structure with an imperfectly bonded interface. Smart Mater. Struct. 21(4), 045009 (2012)

    Article  Google Scholar 

  12. Hakoda, C., Pantea, C., Chillara, V.K.: Engineering the beat phenomenon of quasi-Rayleigh waves for regions with minimal Surface Acoustic Wave (SAW) amplitude. J. Sound Vib. 515, 116444 (2021)

    Article  Google Scholar 

  13. Bandhu, L., Nash, G.R.: Controlling the properties of surface acoustic waves using graphene. Nano Res. 9(3), 685–691 (2016)

    Article  Google Scholar 

  14. Tang, G., et al.: Enhancement of effective electromechanical coupling factor by mass loading in layered surface acoustic wave device structures. Jpn. J. Appl. Phys. 55(7), 07KD07 (2016)

    Article  Google Scholar 

  15. Goyal, R., Kumar, S., Sharma, V.: A size-dependent micropolar-piezoelectric layered structure for the analysis of Love wave. Waves Random Complex 30(3), 544–561 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Wang, W.H., et al.: Surface wave speed of functionally gradient piezoelectric semiconductors. Arch. Appl. Mech. 92(6), 1905–1912 (2022)

    Article  Google Scholar 

  17. Chaudhary, S., Sahu, S.A., Paswan, B.: Transference of SH waves through irregular interface between corrugated piezoelectric layer and prestressed viscoelastic substrate. Mech. Adv. Mater. Struct. 26(2), 156–169 (2019)

    Article  Google Scholar 

  18. Singh, B.: Propagation of shear waves in a piezoelectric medium. Mech. Adv. Mater. Struct. 20(6), 434–440 (2013)

    Article  Google Scholar 

  19. Nirwal, S., et al.: Analysis of different boundary types on wave velocity in bedded piezo-structure with flexoelectric effect. Compos. Part. B Eng. 167, 434–447 (2019)

    Article  Google Scholar 

  20. Nie, G., Liu, J., Liu, X.: Lamb wave propagation in a piezoelectric/piezomagnetic bi-material plate with an imperfect interface. Acta. Acust. United Acust. 102(5), 893–901 (2016)

    Article  Google Scholar 

  21. Pang, Y., et al.: SH wave propagation in a piezoelectric/piezomagnetic plate with an imperfect magnetoelectroelastic interface. Waves Random Complex 29(3), 580–594 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  22. Rakshit, S., et al.: Effect of interfacial imperfections on SH-wave propagation in a porous piezoelectric composite. Mech. Adv. Mater. Struct. (2021)

  23. Wang, H.M., Zhao, Z.C.: Love waves in a two-layered piezoelectric/elastic composite plate with an imperfect interface. Arch. Appl. Mech. 83(1), 43–51 (2013)

    Article  MATH  Google Scholar 

  24. Iglesias, F.S., Lopez, A.F.: Rayleigh damping parameters estimation using hammer impact tests. Mech. Syst. Signal Process. 135, 106391 (2020)

    Article  Google Scholar 

  25. Chanda, A., Sahoo, R.: Forced vibration responses of smart composite plates using Trigonometric Zigzag theory. Int. J. Struct. Stab. Dyn. 21(05), 2150067 (2021)

    Article  MathSciNet  Google Scholar 

  26. Sonner, M.M., et al.: High-dimensional acousto-optoelectric correlation spectroscopy reveals coupled carrier dynamics in polytypic nanowires. Phys. Rev. Appl. 16(3), 034010 (2021)

    Article  Google Scholar 

  27. Ma, C.C., Chen, X.H., Ing, Y.S.: Theoretical transient analysis and wave propagation of piezoelectric bi-materials. Int. J. Solids Struct. 44(22–23), 7110–7142 (2007)

    Article  MATH  Google Scholar 

  28. Lin, Y.H., Ing, Y.S., Ma, C.C.: Two-dimensional transient analysis of wave propagation in functionally graded piezoelectric slabs using the transform method. Int. J. Solids Struct. 52, 72–82 (2015)

    Article  Google Scholar 

  29. Ing, Y.S., Liao, H.F., Huang, K.S.: The extended Durbin method and its application for piezoelectric wave propagation problems. Int. J. Solids Struct. 50(24), 4000–4009 (2013)

    Article  Google Scholar 

  30. Li, S.F.: The electromagneto-acoustic surface wave in a piezoelectric medium the Bleustein-Gulyaev mode. J. Appl. Phys. 80(9), 5264–5269 (1996)

    Article  Google Scholar 

  31. Li, S.F.: Transient wave propagation in a transversely isotropic piezoelectric half space. Z. Angew. Math. Phys. 51(2), 236–266 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  32. Bajpai, A., Sharma, P.K., Kumar, R.: Transient response of a thermo-diffusive elastic thick circular plate with variable conductivity and diffusivity. Acta. Mech. 232(9), 3343–3361 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhou, X., Shui, G.: Propagation of transient elastic waves in multilayered composite structure subjected to dynamic anti-plane loading with thermal effects. Compos. Struct. 241, 112098 (2020)

    Article  Google Scholar 

  34. Shariyat, M.: Nonlinear transient stress and wave propagation analyses of the FGM thick cylinders, employing a unified generalized thermoelasticity theory. Int. J. Mech. Sci. 65(1), 24–37 (2012)

    Article  Google Scholar 

  35. Ashida, F., Morimoto, T., Ohtsuka, T.: Dynamic behavior of thermal stress in a functionally graded material thin film subjected to thermal shock. J. Therm. Stress. 37(9), 1037–1051 (2014)

    Article  Google Scholar 

  36. Wang, Y., Li, M., Liu, D.: Transient thermo-mechanical analysis of FGM hollow cylindrical structures involving micro-scale effect. Thin Walled Struct. 164, 107836 (2021)

    Article  Google Scholar 

  37. Tiersten, H.F.: Linear piezoelectric plate vibrations. Plenum Press, New York (1969)

    Book  Google Scholar 

  38. Rose, J.L.: Ultrasonic waves in solid media. Cambridge University Press, London (2000)

    Book  Google Scholar 

  39. Cagniard, L.: Reflexion et refraction des ondes seismiques progressives. Cauthiers-Villars, Paris (1939)

    MATH  Google Scholar 

  40. De Hoop, A.T.: A modification of Cagniard’s method for solving seismic pulse problems. Appl. Sci. Res. B 8, 349–356 (1960)

    Article  MATH  Google Scholar 

  41. Sanchez-Sesma, F.J., Iturraran-Viveros, U.: The classic Garvin’s problem revisited. B. Seismol. Soc. Am. 96(4), 1344–1351 (2006)

    Article  Google Scholar 

  42. Shan, Z., Ling, D.: An analytical solution for the transient response of a semi-infinite elastic medium with a buried arbitrary cylindrical line source. Int. J. Solids. Struct. 100, 399–410 (2016)

    Article  Google Scholar 

  43. Dehestani, M., et al.: Computation of the stresses in a moving reference system in a half-space due to a traversing time-varying concentrated load. Comput. Math. Appl. 65(11), 1849–1862 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  44. Lee, G.S., Ma, C.C.: Transient elastic waves propagating in a multi-layered medium subjected to in-plane dynamic loadings. I. Theory. P. Roy. Soc. A Math. Phys. 456(1998), 1355–1374 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  45. Ma, C.C., Lee, G.S.: Transient elastic waves propagating in a multi-layered medium subjected to in-plane dynamic loadings. II. Numerical calculation and experimental measurement. P. Roy. Soc. A Math. Phys. 456(1998), 1375–1396 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  46. Ma, C.C., Liu, S.W., Lee, G.S.: Dynamic responses of a layered medium subjected to anti-plane loadings. Int. J. Solids. Struct. 38(50–51), 9295–9312 (2001)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

Support from the National Natural Science Foundation of China (No. 12272036) is greatly appreciated.

Author information

Authors and Affiliations

  1. Department of Mechanics, Beijing Jiaotong University, Beijing, 100044, China

    Fangzhi Wu, Xiang Zhou & Guoshuang Shui

Authors
  1. Fangzhi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiang Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guoshuang Shui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Xiang Zhou or Guoshuang Shui.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

The transient response of the displacement field can be expressed as:

$$ \frac{{\pi \tilde{c}_{44} L}}{{c_{s} P}}w^{\prime}\left( {x,y,t} \right) = \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right) - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} $$
(104)

The transient response of electrical potential, stress and electric displacement can be expressed as:

$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} \in_{{{11}}} L}}{{\tau_{0} c_{s} e_{15} }}\phi^{\prime}\left( {x,y,t} \right) = \frac{{C_{f} }}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] - {\text{Re}} \left( {{\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$
(105)
$$ \begin{gathered} \frac{\pi L}{{\tau_{0} }}\tau_{{{\text{yz}}}} \left( {x,y,t} \right) = \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } {\Omega }_{a}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{ae}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\;\;\;\;\quad + k_{e}^{2} {\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$
(106)
$$ \begin{gathered} \frac{\pi L}{{\tau_{0} }}\tau_{{{\text{xz}}}} \left( {x,y,t} \right){ = } - \frac{1}{{{1} - k_{{\text{e}}}^{4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- {\text{Im}} \left( {\vartheta_{ae}^{\prime + } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { \quad+ k_{{\text{e}}}^{2} {\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{e}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$
(107)
$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} L}}{{\tau_{0} e_{15} }}D_{y} \left( {x,y,t} \right) = \frac{1}{{{1} - k_{{\text{e}}}^{4} }}\left\{ {\left( {1 - C_{f} } \right){\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad - \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\quad + C_{{\text{f}}} {\text{Re}} \left( {\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$
(108)
$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} L}}{{\tau_{0} e_{15} }}D_{{\text{x}}} \left( {x,y,t} \right) = - \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad+ C_{{\text{f}}} \left. {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$
(109)

where

$$ \begin{gathered} {\Omega }_{{\text{a}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } + k_{{\text{e}}}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{a}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{{\text{a}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{a}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \tau_{a}^{2} } }} \hfill \\ {\Omega }_{{{\text{ae}}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } + k_{e}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{ae}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\sqrt {\tau_{a}^{2} - \tau^{2} } }} \hfill \\ {\Omega }_{{\text{e}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{a}^{\prime + 2} } + k_{e}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{a}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{e}^{\prime + 2} }}\frac{{\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \left( {x^{\prime 2} + q^{2} y^{\prime 2} } \right)\tau_{l}^{2} } }} \hfill \\ \end{gathered} $$
(110)
$$ \begin{gathered} \vartheta_{a}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \pm {\text{i}}\frac{{qy^{\prime}\sqrt {\tau^{2} - \left( {x^{\prime 2} + q^{2} y^{\prime 2} } \right)} }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \hfill \\ \vartheta_{ae}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \pm \frac{{qy^{\prime}\sqrt {\left( {x^{\prime 2} + q^{2} y^{{\prime}{2}} } \right) - \tau^{2} } }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \hfill \\ \vartheta_{e}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + y^{\prime 2} }} \pm {\text{i}}\frac{{y^{\prime}\sqrt {\tau^{2} - \left( {x^{\prime 2} + y^{\prime 2} } \right)\tau_{l}^{2} } }}{{x^{\prime 2} + y^{\prime 2} }} \hfill \\ \end{gathered} $$
(111)

Appendix 2

After dimensionless processing, each physical quantity can be expressed as:

$$ \frac{{\pi c_{44}^{v} L}}{{c_{s} \tau^{v} }}w^{\prime}\left( {x,y,t} \right){ = }\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{a}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right) - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} $$
(112)
$$ \begin{gathered} \frac{{\pi c_{44}^{v} \in_{{{11}}} L}}{{\tau^{v} c_{{\text{s}}} e_{15} }}\phi^{\prime}\left( {x,y,t} \right) = \frac{{C_{f} }}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\Omega_{a}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\Omega_{ae}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{ \in_{{{11}}} }}{{ \in_{0} }}\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\Omega_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{e} } \right)} \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\text{Im}} \left( {\Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{ \in_{{{11}}} }}{{ \in_{0} }}\frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{cf} \in_{11} }} + \frac{{e_{15}^{{2}} }}{{ \in_{11} + \in_{0} }}}}\left\{ {{\text{Re}} \left( {\Omega_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\Omega_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$
(113)
$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} \tilde{c}_{44} }}\tau_{yz} \left( {x,y,t} \right){ = }\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{a}^{\prime + 2} } {\Omega }_{a}^{v\prime } } \right)\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{a} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{e_{15}^{2} }}{{\tilde{c}_{44} \in_{0} }}\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } {\Omega }_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{e} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } {\Omega }_{ef1}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{ef} } \right) - H\left( {\tau - \tau_{e} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{e_{15} }}{{\frac{{e_{15} }}{{E_{cf} \in_{11} }} + \frac{{e_{15} }}{{ \in_{11} + \in_{0} }}}}\frac{{c_{44}^{v} }}{{\tilde{c}_{44} \in_{0} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } {\Omega }_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } {\Omega }_{ef2}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$
(114)
$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} \tilde{c}_{44} }}\tau_{{{\text{xz}}}} \left( {x,y,t} \right) = - \frac{1}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } \Omega_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } \Omega_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{{e_{15}^{2} }}{{\tilde{c}_{44} \in_{0} }}\frac{1}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } \Omega_{{{\text{e}}1}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } \Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{e_{15} }}{{\frac{{e_{15} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15} }}{{ \in_{11} + \in_{0} }}}}\frac{{c_{44}^{v} }}{{\tilde{c}_{44} \in_{0} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } \Omega_{{{\text{e}}2}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } \Omega_{ef2}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$
(115)
$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} e_{15} }}D_{{\text{y}}} \left( {x,y,t} \right) = \frac{{1 - C_{{\text{f}}} }}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } \Omega_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } \Omega_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{ \in_{11} }}{{ \in_{0} \left( {1 - k_{v}^{4} } \right)}}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \Omega_{{{\text{e}}1}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; - \frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15}^{2} }}{{ \in_{11} + \in_{0} }}}}\frac{{ \in_{11} }}{{ \in_{0} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \Omega_{{{\text{e}}2}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \Omega_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$
(116)
$$ \begin{gathered} \frac{{\pi c_{44}^{{\text{v}}} L}}{{\tau^{{\text{v}}} e_{15} }}D_{{\text{x}}} \left( {x,y,t} \right){ = } - \frac{{1 - C_{{\text{f}}} }}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } {\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{{ \in_{11} }}{{ \in_{0} \left( {1 - k_{v}^{4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{e}^{\prime + } {\Omega }_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } {\Omega }_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15}^{2} }}{{ \in_{11} + \in_{0} }}}}\frac{{ \in_{11} }}{{ \in_{0} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. {\quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } {\Omega }_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$
(117)
$$ \begin{gathered} \Omega_{{\text{a}}}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } + k_{{\text{e}}}^{v2} \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{a}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{\text{a}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \tau_{{\text{a}}}^{2} } }} \hfill \\ \Omega_{{{\text{ae}}}}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } + k_{e}^{v2} \sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\sqrt {\tau_{{\text{a}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$
(118)
$$ \begin{gathered} \Omega_{e1}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{e}}}^{\prime + 2} } + k_{{\text{e}}}^{v2} \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{\text{e}}}^{\prime + 2} }} \cdot \hfill \\ \frac{{\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \left[ {\left( {1 - C_{{\text{f}}} } \right)q\sqrt {1 - \vartheta_{{\text{e}}}^{\prime + 2} } - \frac{{ \in_{0} }}{{ \in_{11} }}C_{{\text{f}}} \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right]}}{{\left( { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right)\sqrt {\tau^{2} - \tau_{{\text{e}}}^{2} } }} \hfill \\ \Omega_{ef1}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + k_{e}^{v2} \sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{{v{2}}} - \vartheta_{{{\text{ef}}}}^{\prime + 2} }} \cdot \hfill \\ \frac{{\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \left[ {\left( {1 - C_{{\text{f}}} } \right)q\sqrt {1 - \vartheta_{{{\text{ef}}}}^{\prime + 2} } - \frac{{ \in_{0} }}{{ \in_{11} }}C_{{\text{f}}} \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]}}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]\sqrt {\tau_{{\text{e}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$
(119)
$$ \begin{gathered} \Omega_{e2}^{v\prime } = \frac{{\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } }}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right]\sqrt {\tau^{2} - \tau_{{\text{e}}}^{2} } }} \hfill \\ \Omega_{ef2}^{v\prime } = \frac{{\sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } }}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]\sqrt {\tau_{{\text{e}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$
(120)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, F., Zhou, X. & Shui, G. Thermal effect on the transient waves in piezoelectric half-space subjected to dynamic loading. Arch Appl Mech 93, 1647–1669 (2023). https://doi.org/10.1007/s00419-022-02351-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02351-7

Keywords

Search

Navigation