Superharmonic-principal parametric joint resonance and stability of an axially variable-speed moving beam between current-carrying wires

Abstract

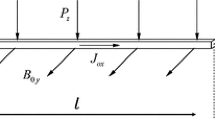
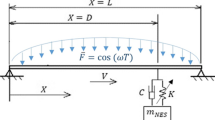
In this paper, the magneto-elastic superharmonic-principal parametric joint resonance of an axially variable-speed moving beam is investigated, where magnetic force generated by parallel current-carrying wires is considered. Based on electromagnetic theory and Hamilton principle, the nonlinear forced vibration equation is derived, and the vibration differential equation is obtained using the Galerkin method. The multiple-scale method is used to solve the differential equation for the analytical solution, and the stability of the steady-state solutions is analyzed. Through an example, the curves of amplitude versus frequency, external excitation, axial velocity, current intensity, and beam position are obtained. The results show that the effect of axial velocity on resonance frequency is significantly larger than that of current intensity. In addition, the increase in current intensity leads to the decrease in amplitude, since the current-carrying wires act as electromagnetic damping. As the current intensity increases and the distance decreases, respectively, the system changes from quasi-periodic motion to single-frequency periodic motion.

Appendices

Appendix A:Integral coefficient expression

$A_{11} = \int_{0}^{l} {\frac{{{\text{d}}^{4} X_{1} }}{{{\text{d}} x^{4} }}} X_{1} {\text{d}} x$, $B_{11} = \int_{0}^{l} {\frac{{{\text{d}}^{2} X_{1} }}{{{\text{d}} x^{2} }}} X_{1} {\text{d}} x$, $C_{11} = \int_{0}^{l} {\frac{{{\text{d}} X_{1} }}{{{\text{d}} x}}} X_{1} {\text{d}} x$, $D_{11} = \int_{0}^{l} {X_{1} } X_{1} {\text{d}} x$, $E_{1} = \int_{0}^{l} {X_{1} } {\text{d}} x$, $H_{11} = \int_{0}^{l} {X_{1}^{2} X_{1} {\text{d}} x}$$K_{11} = \int_{0}^{l} {\frac{{{\text{d}} X_{1} }}{{{\text{d}} x}}X_{1} } X_{1} {\text{d}} x$, $M_{11} = \int_{0}^{l} {X_{1}^{3} X_{1} {\text{d}} x}$, $N_{11} = \int_{0}^{l} {\frac{{{\text{d}} X_{1} }}{{{\text{d}} x}}} X_{1}^{2} X_{1} {\text{d}} x$, $S_{11} = \int_{0}^{l} {\frac{{{\text{d}}^{2} X_{1} }}{{{\text{d}} x^{2} }}\left( {\frac{{dX_{1} }}{dx}} \right)}^{2} X_{1} {\text{d}} x$.

Appendix B: The parameters in Eq. (10)

$q_{1} (\tau ) = \frac{{q_{1} (t)}}{h}$, ${\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \omega_{0} = p_{1}^{2} \sqrt {\frac{EI}{{\rho A}}{\kern 1pt} } {\kern 1pt}$, ${\kern 1pt} {\kern 1pt} {\kern 1pt} \tau = {\kern 1pt} \omega_{0} t{\kern 1pt}$, ${\kern 1pt} \eta = \frac{{c_{0} }}{{\omega_{0} }}$, $\zeta = \frac{{F_{o} }}{{\rho A\omega_{0}^{2} }}$, $\mu_{11}^{\prime } = \frac{{2c_{1} C_{11} }}{{\omega_{0} D_{11} }}$, $\mu_{11} = \frac{{\sigma_{0} \mu_{0}^{2} \alpha_{1}^{2} D_{11} }}{{4{\uppi }^{2} \rho \omega_{0} D_{11} }} + \frac{{2c_{0} C_{11} }}{{\omega_{0} D_{11} }}$, $g_{1}^{2} = \frac{{\eta^{2} B_{11} }}{{D_{11} }} - \frac{{\zeta B_{11} }}{{D_{11} }} + \frac{{EIA_{11} }}{{\rho A\omega_{0}^{2} D_{11} }} + \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{1}^{2} c_{0} C_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }} + \frac{{c_{1}^{2} B_{11} }}{{2\omega_{0}^{2} D_{11} }}$, ${\kern 1pt} \Omega_{1} = \frac{{\omega_{1} }}{{\omega_{0} }}$, ${\kern 1pt} \Omega_{2} = \frac{{\omega_{2} }}{{\omega_{0} }}$, ${\kern 1pt} \Omega_{3} = \frac{{\omega_{3} }}{{\omega_{0} }}$,$\delta_{111} = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{1}^{2} c_{1} C_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }} + \frac{{2c_{0} c_{1} B_{11} }}{{\omega_{0}^{2} D_{11} }}$,

$\delta_{211} = \frac{{c_{1}^{2} B_{11} }}{{2\omega_{0}^{2} D_{11} }}$, $\delta_{311} = \frac{{ - F_{1} B_{11} }}{{\rho A\omega_{0}^{2} D_{11} }}$, $\delta_{411} = \frac{{ - c_{1} C_{11} }}{{\omega_{0} D_{11} }}$, $\chi_{11} = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{2} c_{0} hK_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }}$, $\chi_{11}^{\prime } = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{2} c_{1} hK_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }}$, ${\kern 1pt} n_{11} = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{3} c_{0} h^{2} N_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }} - \frac{{3ES_{11} h^{2} }}{{2\rho \omega_{0}^{2} D_{11} }}$, ${\kern 1pt} n_{11}^{\prime } = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{3} c_{1} h^{2} N_{11} }}{{4{\uppi }^{2} \rho \omega_{0}^{2} D_{11} }}$, $h_{11} = \frac{{\mu {}_{0}^{2} \sigma_{0} \alpha_{2} H_{11} h}}{{4{\uppi }^{2} \rho D_{11} \omega_{0} }}$, $m_{11} = \frac{{\mu_{0}^{2} \sigma_{0} \alpha_{3} M_{11} h^{2} }}{{4{\uppi }^{2} \rho D_{11} \omega_{0} }}$, $f_{1} = \frac{{P_{0} E_{1} }}{{D_{11} \rho \omega_{0}^{2} hA}}$.

Appendix C: The parameters in Eq. (25)

$$j_{11} = \frac{1}{{g_{1} }}[ - \frac{1}{2}g_{1} \mu_{11} - \left( {\frac{{3m_{11} }}{4}a_{10}^{2} g_{1} + m_{11} \Lambda_{1}^{2} g_{1} + m_{11} \Lambda_{1}^{2} \Omega_{3} } \right) - \left( {\frac{{\delta_{111} }}{4} + \frac{{9n_{11}^{\prime } }}{16}a_{10}^{2} + \frac{{3n_{11}^{\prime } }}{2}\Lambda_{1}^{2} } \right)\sin 2\phi_{40}$$

$+ \frac{{\mu_{11}^{\prime } }}{4}g_{1} \cos 2\phi_{40} - \frac{{\delta_{311} }}{4}\sin 2\phi_{40} ]$,

$j_{12} = \frac{1}{{g_{1} }}\left[ { - 2\gamma_{20} \cos 2\phi_{40} + 2\gamma_{70} \sin 2\phi_{40} - 2\gamma_{30} \cos 2\phi_{40} - \gamma_{40} \cos \phi_{40} + \gamma_{50} \sin \phi_{40} - \gamma_{60} \cos \phi_{40} } \right]$,

$j_{21} = \frac{1}{{g_{1} }}\left[ { - \left( {\frac{3}{4}n_{11} a_{10} } \right) - \left( {\frac{{3n_{11}^{\prime } }}{8}a_{10} } \right)\cos 2\phi_{40} + n_{11} \Lambda_{1}^{3} \frac{1}{{a_{10}^{2} }}\cos \phi_{40} - m_{11} \Lambda_{1}^{3} \Omega_{3} \frac{1}{{a_{10}^{2} }}\sin \phi_{40} + \frac{{n^{\prime}_{11} }}{2}\Lambda_{1}^{3} \frac{1}{{a_{10}^{2} }}\cos \phi_{40} } \right]$,

$j_{22} = \frac{1}{{a_{10} g_{1} }}\left[ {2\gamma_{20} \sin 2\phi_{40} + 2\gamma_{70} \cos 2\phi_{40} + 2\gamma_{30} \sin 2\phi_{40} + \gamma_{40} \sin \phi_{40} + \gamma_{50} \cos \phi_{40} + \gamma_{60} \sin \phi_{40} } \right]$,

$\gamma_{50} = m_{11} \Lambda_{1}^{3} \Omega_{3}$, $\gamma_{60} = \frac{{n^{\prime}_{11} }}{2}\Lambda_{1}^{3}$, $\gamma_{70} = - \frac{{\mu_{11}^{\prime } }}{4}a_{10} g_{1}$, $\gamma_{20} = \frac{{\delta_{111} }}{4}a_{10} + \frac{{3n_{11}^{\prime } }}{16}a_{10}^{3} + \frac{{3n_{11}^{\prime } }}{2}a_{10} \Lambda_{1}^{2}$, $\gamma_{30} = \frac{{\delta_{311} }}{4}a_{10}$, $\gamma_{40} { = }n_{11} \Lambda_{1}^{3}$.