Skip to main content

Advertisement

SpringerLink
Log in

The method for solving topology optimization problems using hyper-dual numbers

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

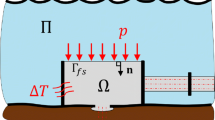
Air-inflated structure such as an air bed, tents, and floats is a category of a high-strength membrane structure design problem. This problem is described as a surface energy minimization problem to make maximum use of limited space. Such problems can be treated as the topology optimization problems. Some topology optimization problems are design problems involving physical phenomena such as heat and structure. When the topology optimization is applied to such problems, it may be difficult to derive the sensitivity of the variation of the objective function analytically, especially in surface energy minimization problems where the volume of the design space is limited. In this study, we apply a numerical differential method using hyper-dual number to the sensitivity of the variation of the objective function, and then show that the desired optimization shape can be obtained even when analytical sensitivity is difficult to derive. By expanding the design variables of the topology optimization problem to the hyper-dual numbers, the sensitivity required to find the solution to the optimization problem can be determined without calculating the variation. The sensitivity obtained using the hyper-dual numbers does not include rounding and truncation errors. As an example of a problem whose sensitivity is difficult to obtain analytically, under the condition that the volume of the given domain is conserved, the solution to the surface minimization problem, which is formulated as a kind of surface energy minimization problem, is obtained by expanding the design variables to the hyper-dual numbers. The proposed method can be used to find solutions to topology optimization problems involving physical phenomena.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Shimoda, M., Yamane, K.: A numerical form-finding method for the minimal surface of membrane structures. Struct. Multidisc. Optim. 51, 333–345 (2015)

    Article  MathSciNet  Google Scholar 

  2. Bendsoe, M.P., Sigmund, O.: Topology Optimization: Theory, Methods, and Applications. Springer Science, Berlin Heidelberg (2003)

    MATH  Google Scholar 

  3. Sigmund, O., Maute, K.: Topology optimization approaches a comparative review. Struct. Multidisc. Optim. 48, 1031 (2013)

    Article  Google Scholar 

  4. Cho, S., Jung, H.S.: Design sensitivity analysis and topology optimization of displacement-loaded non-linear structures. Comput. Meth. Appl. Mech. Eng. 192, 22–24 (2003)

    Article  Google Scholar 

  5. Choi, K.K., Kim, N.H.: Structural Sensitivity Analysis and Optimization 2: Nonlinear System and Application. Springer, New York (2005)

    Google Scholar 

  6. Fike, JA., Alonso, JJ.: (2011) The development of hyper-dual numbers for exact second-derivative calculations. In: 49th AIAA Aerospace Sciences Meeting 886:4–7

  7. Fike, JA.: (2013) Multi-objective optimization using hyper-dual numbers. Ph.D thesis, Stanford university

  8. Fike, J.A.: Derivative Calculations using Hyper-Dual Numbers. Technical Report, Sandia National Laboratories (2016)

    Google Scholar 

  9. Neuenhofen, M.: (2018) Review of theory and implementation of hyper-dual numbers for first and second order automatic differentiation. CoRR

  10. Fike, JA., Jongsma, S., Alonso, JJ., Weide, EVD.: (2011) Optimization with gradient and hessian information calculated using hyper-dual numbers. In: 29th AIAA Applied Aerodynamics Conference 3807:27–30

  11. Fike, JA., Alonso, JJ.: (2012) Automatic differentiation through the use of hyper-dual numbers for second derivatives. In: 6th International Conference on Automatic Differentiation 23–27

  12. Endo, VT.: (2020) Hyper-dual sensitivity analysis: a second-order evaluation in structural problems. Ph.D thesis, Federal University of Santa Catarina

  13. Endo, V.T., Fancello, E.A., Muñoz-Rojas, P.A.: Second-order design sensitivity analysis using diagonal hyper-dual numbers. Int. J. Num. Meth. Eng. 122(23), 7134–7155 (2021)

    Article  MathSciNet  Google Scholar 

  14. Tanaka, M., Sasagawa, T., Omote, R., Fujikawa, M., Balzani, D., Schröder, J.: A highly accurate 1st- and 2nd- order differentiation scheme for hyperelastic material models based on hyper-dual numbers. Comp. Meth. Appl. Mech. Eng. 283, 22–45 (2015)

    Article  MathSciNet  Google Scholar 

  15. Endo, V.T., Fancello, E.A., Muñoz-Rojas, P.A.: A study on the computational effort of hyper-dual numbers to evaluate derivatives in geometrically nonlinear hyperelastic trusses. J. Braz. Soc. Mech. Sci. Eng. 43(34), 1–15 (2021)

    Google Scholar 

  16. Cohen, A., Shoham, M.: Application of hyper-dual numbers to multibody kinematics. J. Mech. Robo. 8(1), 11–15 (2016)

    Google Scholar 

  17. Cohen, A., Shoham, M.: Application of hyper-dual numbers to rigid bodies equations of motion. Mech. Mach. Theory 111, 76–84 (2017)

    Article  Google Scholar 

  18. Brake, M.R.W., Fike, J.A., Topping, S.D.: Parameterized reduced order models from a single mesh using hyper-dual numbers. J. Sound. Vib. 371, 370–392 (2016)

    Article  Google Scholar 

  19. Szirmay-Kalos, L.: Higher order automatic differentiation with dual numbers. Period. Polytech. Electr. Eng. Comp. Sci. 65(1), 1–10 (2021)

    Google Scholar 

  20. Bonnans, J.F., Gilbert, J., Lemaréchel, C., Sagastizábal, C.A.: Numerical optimization: theoretical and practical aspects. Springer (2003)

  21. Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (2006)

  22. Meeks, W.H.I.I.I., Pérez, J.: The classical theory of minimal surface. Bull. Amer. Math. Soc. 48(3), 325–407 (2011)

    Article  MathSciNet  Google Scholar 

  23. de Gennes, P.G., Brochard-Wyart, F., Quéré, D.: Capillarity and Wetting Phenomena: Drops. Bubbles, Pearls, Waves, Springer (2004)

    Book  Google Scholar 

  24. Azegami, H., Kaitsu, S., Takeuchi, K.: Regular solution to topology optimization problems of continua. JSIAM Lett. 3, 1–4 (2011)

    Article  MathSciNet  Google Scholar 

  25. Azegami, H.: Shape optimization problems. Springer (2020)

  26. Kuhn, HW., Tucker, AW.: (1951) Nonlinear programing. Proceedings of 2nd Berkeley Symposium, Berkeley 2:481–492

  27. Antoniou, A., Lu, W.S.: Practical optimization algorithms and engineering applications. Springer (2007)

  28. Kawamoto, A., Matsumori, T., Kondoh, T., Yamasaki, S., Nishiwaki, S.: Topology optimization by a time-dependent diffusion equation. Int. J. Num. Meth. Eng. 93(8), 795–817 (2013)

    Article  MathSciNet  Google Scholar 

  29. Murai, D., Kawamoto, A., Kondoh, T.: Shape optimization using time evolution equations. Int. J. Num. Meth. Eng. 115(11), 1371–1382 (2018)

    Article  MathSciNet  Google Scholar 

  30. Murai, D., Kawamoto, A., Kondoh, T.: Solution to the topology optimization problem using a time-evolution equation. Int. J. Num. Meth. Eng. 121(10), 2246–2261 (2020)

    Article  MathSciNet  Google Scholar 

  31. Chung, TJ.: (2002) Computational fluid dynamics. Cambridge University

  32. Wilmott, P., Howison, S., Dewynne, J.: (1995) The mathematics of financial derivatives a student introduction. Cambridge University

  33. Olver, P.J.: Introduction to partial differential equations. Springer (2013)

Download references

Acknowledgements

We would like to thank Editage (www.editage.com) for English editing.

Author information

Authors and Affiliations

  1. TOYOTA Central Research and Development Laboratories Incorporated, 41–1 Yokomichi, Nagakute, Aichi, 480–1192, Japan

    Daisuke Murai, Ryuji Omote & Masato Tanaka

Authors
  1. Daisuke Murai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ryuji Omote
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Masato Tanaka
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daisuke Murai.

Ethics declarations

Conflict of interest

Not applicable.

Funding

Not applicable.

Data availability and materials

Not applicable.

Code availability

In this calculation, python code is created to discretize the design variables and objective and constraint functions. If necessary, we can disclose the source code used in the calculation.

Authors’ contributions

All authors contributed to the study conception and design. Material preparation and numerical calculation were performed by Daisuke Murai and Ryuji Omote. The algebraic and transcendental functions using hyper-dual number were formulated by Masato Tanaka. The python program for hyper-dual number using operator overloading was created by Ryuji Omote. The first draft of the manuscript was written by Daisuke Murai and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Murai, D., Omote, R. & Tanaka, M. The method for solving topology optimization problems using hyper-dual numbers. Arch Appl Mech 92, 2813–2824 (2022). https://doi.org/10.1007/s00419-022-02183-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02183-5

Keywords

Search

Navigation