Skip to main content
SpringerLink
Log in

Linearised response of arched structures under pulse-type excitation

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

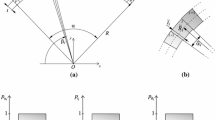
Seismic response of masonry arches is examined in this study through analytical and numerical methods. Emphasis is placed on the low-amplitude levels where linearisation techniques may be efficient. When dealing with monumental arches of fragmented masonry, rocking rotation even in low levels is most often undesirable as it may lead to severe permanent displacements and dislocation of the arch axis, and sometimes to general instability of the structure. It is therefore of great importance to develop simplified procedures for estimating the levels of such low-amplitude arch response in earthquake-prone regions. Near-source ground excitation at the base of the structure is idealised with rectangular and cycloidal pulses. The analysis is limited to the prior-to-impact regime in which rocking occurs between successive fragments (voussoirs). This limitation does not prevent from extracting conclusions, as the prior-to-impact state is the most crucial to rocking response and it can determine whether the structure will undergo rocking vibration or eventually overturns. For simplicity, a specific kinematic mechanism of the fragmented arch, well known in the literature, is implemented throughout the study, thus allowing for comparison of the results with existing solutions. This idealisation is justified as the predominant mechanism from both previous analytical and experimental studies. A good correlation of the results between simplified closed-form solutions and rigorous semi-analytical methods is accomplished. Moreover, these results are also quite close to those of the 2D finite element analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Coulomb, C.A.: Theorie des machines simples (1821)

  2. Couplet, P.: De la poussée des voûtes, Histoire de l’Académie Royale des Sciences, pp. 79–117, 117–141. Académie royale des sciences, Paris (1729, 1730)

  3. Heyman, J.: The stone skeleton. Int. J. Solids Struct. 2, 249–279 (1966)

    Article  Google Scholar 

  4. Heyman, J.: The Masonry Arch. Ellis Horwood, Chichester (1982)

    Google Scholar 

  5. Heyman, J.: The safety of masonry arches. Int. J. Mech. Sci. 11, 363–385 (1969)

    Article  Google Scholar 

  6. Oppenheim, I.J.: The masonry arch as a four-link mechanism under base motion. Earthq. Eng. Struct. Dyn. 21, 1005–1017 (1992)

    Article  Google Scholar 

  7. Housner, G.W.: The behaviour of inverted pendulum structures during earthquakes. Bull. Seismol. Soc. Am. 53(2), 403–417 (1963)

    Google Scholar 

  8. Clemente, P.: Introduction to dynamics of stone arches. Earthq. Eng. Struct. Dyn. 27, 513–522 (1998)

    Article  Google Scholar 

  9. De Lorenzis, L., DeJong, M., Ochsendorf, J.: Failure of masonry arches under impulse base motion. Earthq. Eng. Struct. Dyn. 36(14), 2119–2136 (2007)

    Article  Google Scholar 

  10. De Jong, M., De Lorenzis, L., Adams, S., Ochsendorf, J.: Rocking stability of masonry arches in seismic regions. Earthq. Spectra 24, 847–865 (2008)

    Article  Google Scholar 

  11. Alexakis, H., Makris, N.: Limit equilibrium analysis and the minimum thickness of circular masonry arches to withstand lateral inertial loading. Arch. Appl. Mech. 84, 757–772 (2014)

    Article  MATH  Google Scholar 

  12. Apostolou, M.: Soil–structure interaction under strong seismic moment: material and geometric nonlinearity. Dissertation, National Technical University of Athens (2011)

  13. Zhang, J., Makris, N.: Rocking response of free-standing blocks under cycloidal pulses. J. Eng. Mech. ASCE 127(5), 473–483 (2001)

    Article  Google Scholar 

  14. Makris, N., Roussos, Y.: Rocking response and overturning of equipment under horizontal pulse-type motions. Rep. No. PEER- 98/05, Pacific Earthquake Engrg. Res. Ctr., University of California, Berkeley, CA (1998)

  15. Coisson, R., Vernizzi, G., Yang, X.: Mathieu functions and Numerical solutions of the Mathieu equation. In: IEEE Proceedings of the International Workshop on Open Source Software for Scientific Computation, pp. 3–10 (2009)

  16. Langer, R.: The solutions of the Mathieu equation with a complex variable and at least one parameter large. Trans. Am. Math. Soc. 36(3), 637–695 (1934)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, National Technical University, Athens, Greece

    A. Leontari & M. Apostolou

Authors
  1. A. Leontari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Apostolou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Leontari.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Leontari, A., Apostolou, M. Linearised response of arched structures under pulse-type excitation. Arch Appl Mech 88, 1121–1137 (2018). https://doi.org/10.1007/s00419-018-1362-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-018-1362-1

Keywords

Search

Navigation