1 Introduction

The need to diagnose damages of rotating machinery, particularly damages associated with the fatigue processes, forces the development of new methods to assess the durability of these devices. The most important is the ability to detect fatigue damage of power trains in their early stage of formation [1]. This applies especially to the diagnosing of the development of gear tooth pitting and fatigue cracks at the tooth base. It is assumed in fact that even 60% of the gear damages are caused by fatigue damage of teeth [2] referred in the literature as local damages to the gears [3]. On the other hand, according to the report of Allianz Versicherungs-Aktiengesellschaft [4], fatigue damage to the teeth and their forced fracture are responsible for 90% damage of gears.

So far in the literature devoted to the problems of machine diagnostic few studies can be found on, for example, detecting the early phases of pitting. According to Combet and Gelman [5], there is high industry demand for methods of early pitting diagnosis when only 5–10% of the tooth surface is damaged. It is mainly related to the development of particularly heavy-duty aircraft power trains (e.g., transmissions in helicopters) and wind turbine gears [6].

The difficulty in getting information about the development of early stages of this type of defects is due to the fact that they cause changes in the vibration signal of a very low energy that are barely detectable. These symptoms are also affected by the impact of manufacturing and assembly errors of cooperating transmission components. The typical lack of stationarity during transmission operation including temporary changes in speed and load [7] further impedes inference in these cases. All these factors make the widely used broadband diagnostic methods based on the average measures of signal such as peak, RMS, kurtosis, as well as methods described in ISO 10816 [8] or recommendations regarding diagnostic systems of wind turbines [9] not reacting early enough for local gear tooth damages.

Variable, cyclic, loading of the gear teeth can cause the initiation of fatigue cracks at the tooth base and later a crack propagation. Fatigue cracks may appear in the tooth base in these places, which are subjected to the greatest stress. Their location can be determined on the basis of numerical analysis, taking into account the variability of the meshing force, the point (line) of its application and its direction due to impaired cooperating gear pairs. Simulation models allowing to verify the recorded real signals and especially to verify the correctness of selected diagnostic parameters are useful for this purpose.

Local damages of gear teeth give rise to a transient, local, disturbances of the vibration signal repeated with every rotation of the transmission shaft, causing the phenomenon of phase and amplitude modulation [10,11,12]. It can also be shown [13] that in the early stages of defect when the energy changes of the signal are particularly low, the signal is dominated by the phenomenon of phase modulation. This type of signal disturbances, manifested in the formation and evolution of the phenomena of amplitude, frequency and multi-parametric modulation, is referred to as low energy [14]. This is due to the fact that the increase in power of the vibroacoustic signal is small compared to the changes in the power of the individual meshing harmonics that resulted from the development of nonlinear effects.

In [15] the interesting method of diagnosis of early stages gear fault detection based on stator current analysis was presented. The method is based on the fact that in case of gear local faults additional components are generated in the mechanical torque that could be seen in the stator current space vector instantaneous frequency (SCSVIF) spectrum.

The main difficulty in the study of these phenomena is due to the fact that the differences in the signal spectrum between amplitude and frequency modulations (particularly in the initial period) are characterized by a small modulation index and are hardly distinguishable. The main differences are apparent in the relationships of phase of sidebands modulating the carrier frequency [16]. The phase relationships between sidebands are also affected by difficulty to determine transfer function of a signal from its source to the transmitter.

Despite these difficulties, until recently, methods associated with the demodulation of the signal were the major proportion of developed methods. They were described in the classic works of McFadden [12] and McFadden and Smith [17], as well as Randall and Sweeney [18] concerning the possibility of the location of the damaged tooth. Among the more recent works, the work of Gelman et al. [2] and review works of Feldman [19, 20] on the Hilbert transform should be mentioned. The idea behind these methods was to get through the demodulated time signal to the damaged area, tooth gear, introducing of local disturbances in the signal.

Another approach for diagnosing early stages of fatigue failures is based on the insight that progress of damage increases the nonlinearity of the system. Note that a natural extension of this proposal is the task of determining the size and type of the nonlinearity on the basis of the analysis of the density of the probability distribution of the nonlinear response. So far, analysis of the higher-order spectrums and the recently obtained results of studies [21, 22] show high diagnostic informativity of nonlinear phenomena accompanying the development of damage. Both the qualitative and quantitative changes in nonlinear effects can be used to evaluate the evolution of the fatigue process resulting in catastrophic failures [23].

In recent years, more and more frequently the time-frequency and wavelet methods are used for the diagnosis of fatigue damage of gears [24,25,26]. These methods allow the location of the signal fragment associated with the local damage. One of them, the method of spectral kurtosis, was developed by Antoni [27], Antoni and Randall [28]. This method allows you to find the local nonstationarities in the signal and select which frequencies are affected by them. The method was adapted by Combet and Gelman [5] to detect pitting in an early stage. An example of its use in the process of diagnosing a tooth crack in the planetary gear of a wind turbine can be found in [6].

The main imperfection of most of these diagnostic methods is that in the process of searching for information, they use integration methods of the recoded signal. These methods are by their nature averaging the analyzed signal. In this way, small changes in the signals, appropriate for the initial phases of development failures, are further minimized by the use of signal processing algorithms.

As one can see from the above, brief, review of diagnostic methods of gear diagnostics, current trends in their development are directed to search for detection of specific damages. More and more methods allow not only for a detection of a fact of deterioration of the technical condition of the transmission, but also the precise determination of location, type and size of the damage. For example in [29], the time-domain fault detection method was presented based on the fast dynamic time warping and correlated kurtosis techniques for this purpose. This method was able to extract periodic impulse excitations caused from the faulty gear tooth using an estimated reference signal that has the same frequency as the nominal gear mesh harmonic and is built using vibration characteristics of the gearbox operated under presumed healthy conditions.

The aim of this study was to present the methodology of creating diagnostic methods enabling the identification of local damages of gears, allowing at the same time precise localization of the damage. The common feature of these methods is the direct use of time signal processing algorithms. Their advantage is the simplicity and speed of action that is of great significance for the implementation in the autonomous transmission diagnostic systems and diagnostic systems working online. The gear model was used to analyze the process of meshing and then the assess influence of various errors on the signal generated by the transmission. It was also used for assessing the sensitivity of diagnostic methods that were later tested during the experiments on a back-to-back test stand.

2 Model of the helical gearbox

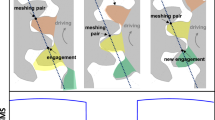
During normal operation mating gear teeth bend under load. The typical approach to dynamic modeling of the transmission [30, 31] is to determine the deflection of mating teeth and by taking into account the variable meshing stiffness, to calculate the meshing force. This approach must take into account that during teeth mating instantaneous points of teeth contact move along the line (or plane in helical gears) of contact, deviating from the theoretical line (or surface). These phenomena were shown in Fig. 1 presenting simulation results for the contact of a single tooth pair of helical gears. Time scale on the figure was set to the simulation points.

Fig. 1
figure 1

Simulated deviations from the plane of action in horizontal and vertical directions for helical gears with axis misalignment

Full size image

The dynamic model of gearbox discussed in this section (Fig. 2) assumes that both wheels have the possibility of making an additional rotation in relation to the constant motion caused by the revolution of their base circles. The resulting interference of tooth profiles can be determined by taking into account the meshing geometry and is being compensated by the flexible deformation of teeth (their deflections) [32, 33]. The meshing stiffness and the changes of its value for the entire path of contact were defined using a 3D FEM models of toothed wheels. The model (Fig. 2) takes into account variable distance between axes resulting from shaft runout or flexible shaft deformation, manufacturing errors such as instantaneous errors of standard contact angle, pitch errors, variable meshing stiffness along the path of contact and more. In case of helical gears, the model assumes division of the face width into several “slices”—spur wheels shifted by a constant angle.

Fig. 2
figure 2

Simplified layout of the dynamic model of the helical gearbox

Full size image

Equations of motion of the model allow observation of time waveforms of several different parameters like displacements, velocities and accelerations of selected coordinates but the most informative from the point of view of analyzing the gearbox behavior are the meshing force and meshing stiffness changes in time. Meshing force was selected as a source of generated signals in the gearbox. Its connection with observation of the meshing stiffness changes allows to associate phenomena observed in the signal with particular contacts.

2.1 Modeling of the manufacturing errors

Manufacturing errors in the model are defined on the single tooth basis. In Fig. 3 examples of two sets of pitch errors (pinion and gear) were presented. These data sets were artificially generated to include three harmonics. Set (b) differs from set (a) with just one tooth error on each of the wheels. These teeth (fourth pinion and fifth gear) have much bigger pitch error for the second set (b) of data. Such approach allows to analyze different kinds of contact in terms of best/worst contact, i.e., contact that has bigger or smaller backlash.

Fig. 3
figure 3

Two sets of simulated pinion (top) and gear (bottom) pitch errors

Full size image

2.2 Modeling of the meshing stiffness with pitting and tooth fracture

In the gearbox model, the pinion and gear rotating systems are coupled by the meshing force (\(\Delta {P}_{{z}}\) in Fig. 2).To calculate the momentary meshing force resulting from the deflections of mating tooth profiles, the knowledge of the meshing stiffness for the current mating point is required. Teeth stiffness of both wheels was calculated using 3D FEM models of gears. Both wheels were modeled independently as spur wheels using SOLID45 elements, used typically for the three-dimensional modeling of solid structures (Fig. 4). The series of static, contactless, FEM calculations were carried out for consecutive places of force application (unit load) on the tooth profiles allowing defining tooth deflections during mating. The meshing stiffness resulting from both tooth deflections was then calculated and approximated by the third-degree polynomial (Fig. 5). Meshing stiffness calculated this way was later verified with data available in the literature [34,35,36].

During the simulation, stiffness of the particular “slices” along the face width was modified depending of their distance from the edge of the wheel (bigger tooth deflection on the edge—Fig. 6).

Fig. 4
figure 4

FEM model of the pinion tooth

Full size image

The crack at the pinion tooth base was modeled as a partial stiffness reduction of the single tooth. The change in tooth stiffness was modeled in FEM by removal of several of the grid elements at the tooth base. Figure 5 shows the result for different sizes of fatigue crack corresponding to the 11 and 21% decrease of stiffness.

Tooth pitting was modeled as a lack of contact on a part of the tooth flank. Figure 6 shows resulting meshing stiffness on consecutive teeth (even and odd) with visible changes across the face width and lack of contact on a part of the teeth as a result of pitting. The authors are aware of the shortcoming of this approach to pitting modeling. It should be probably expanded of friction changes due to roughness of the sliding surfaces.

Fig. 5
figure 5

FEM modeling of teeth deflections due to load and fatigue crack at the pinion tooth base

Full size image
Fig. 6
figure 6

Meshing stiffness changes along face width of teeth and path of contact with lack of contact due to pitting

Full size image

3 Verification of the model

Comparison of simulation results with the signals recorded from the actual transmission is inherently difficult because of the types of signals available for registration. Typically, we are limited to an easily measurable signal of vibration acceleration of the body, or (rarely) rotational velocity changes of both shafts (torsional vibrations). Measurement of vibration acceleration signals, as already mentioned above, is subject to unknown as we do not know the exact path of signal transition from the signal source (meshing), through the shafts, and the body to the point of measurement (sensor). Taking the propagation path in the model into account is usually difficult to implement and verify in practice. It requires special measurement techniques to determine the frequency transfer function (FRF), in which the precise application of the impulse force the gear teeth is the most difficult task. Another problem is caused by usually unknown manufacturing and assembly errors of the gearbox that are difficult to determine.

In order to verify the quality of the model, authors decided to implement a different approach. The waveforms of the total meshing force (sum of current meshing force on all tooth pairs being in contact) obtained through simulation (Fig. 7) were compared with gearbox case acceleration waveforms recorded during the experiments on the back-to-back tester [38]. The test stand, rotating with 25 Hz, was equipped with spur gears (\(m=4\), \(z_{1}=27\), \(z_{2}=35\)), so in the next sections all the presented simulation results will be related to similar gears. During the simulation, pitch errors shown in Fig. 3a were used and several model parameters were modified to obtain the best similarity of time waveforms. More information about the selection of model parameters and methods for the assessment of their sensitivity on the simulation results can be found in [37].

Fig. 7
figure 7

Simulated meshing force (top to down): without errors and with pitch errors from Fig. 3a, b

Full size image

To compare the model with real data, gearbox acceleration signals, averaged synchronously with the rotation of the pinion shaft, recorded on the back-to-back tester were used. The experiment on the test stand was run until breaking of a pinion tooth (72 min). The gears were not modified before the experiment, in particular no preliminary undercuts or damage to teeth were introduced [38]. As mentioned above, simulated meshing force was chosen for comparison (Fig. 7). Since both signals have different dynamics to enable them to be compared each time the signals were rescaled so that their maximum amplitude had a value of 1.

Fig. 8
figure 8

The initial stage of fatigue damage of the tooth pinion (65 min): accelerations versus simulated meshing force (top), modeled meshing stiffness (bottom)

Full size image

Waveforms presented on upper diagrams of Figs. 8 and 9 confirm good compliance of simulated (blue lines) and recorded (red lines) signals despite of their origins and some incompatibilities between the model and the test stand layouts. The amount of stiffness reduction in damaged (modeled) pinion tooth was selected to obtain the best coincidence of the signals thus allowing estimation of the crack size that was otherwise impossible to determine without disassembling the gearbox.

To analyze the processes occurring during the mating of teeth, simulated and recorded signal waveforms were compared with waveforms of meshing stiffness (Figs. 8, 9, 10). Signal fragments shown on these figures correspond to about half of the revolution of the pinion shaft. Figure 8 corresponds to the state in the 65th min of the experiment, lasting a total of about 72 min. Recorded acceleration signal allows to see the first, slight, symptoms of fatigue degradation of the pinion tooth. Using simulated waveforms of the meshing stiffness (single contact stiffness and total stiffness as well), this position on the chart was marked with vertical cursors indicating changes in the conditions of teeth cooperation, respectively: damaged tooth entering two pair contact, beginning of the single tooth contact of this tooth, beginning and exiting of its two pair contact. The latter is the end of contact of the damaged tooth. The recorded signal is compared with the results of the simulation in which the stiffness of all the teeth was the same (undamaged teeth). It is worth mentioning that despite the fact that pitch errors were chosen at random (Fig. 3a) and other manufacturing and assembly errors were omitted during the simulation both analyzed signals looks very similar.

Fig. 9
figure 9

Progress of the fatigue crack of the pinion tooth (68 min); stiffness on the pinion tooth reduced by 6%

Full size image

Figure 9 corresponds to the state in the 68th min of the experiment, when local fluctuations of the signal’s amplitude due to the emerging crack at the tooth base are visible. Simulation was performed for a 6% reduction of the stiffness on one pinion tooth. It is worth noting that due to various manufacturing and assembly errors of the transmission, recorded signal amplitude at the damaged tooth continues not to exceed the peak amplitude of the entire signal.

Fig. 10
figure 10

Final phase of the experiment (70.5 min); stiffness on the pinion tooth reduced by 20%

Full size image

Figure 10 shows the state immediately preceding the breaking of the pinion tooth (70.5 min). Corresponding meshing force simulation was performed using 20% stiffness reduction of the pinion tooth. Note the significantly increased level of signal’s envelope at the moment of beginning of two pair contact while single pair contact was of the damaged tooth. This is due to its additional deflection caused by lower stiffness necessary to transmit the load. The entering into contact of the next pair is rougher in this case. The next meshing force increase is during exiting from contact of the damaged tooth.

4 Local faults detection in gears

Examples of signals presented in the previous chapter emphasize already mentioned problems existing during early stage of failure diagnostics. Changes in the signal amplitude are too small to be detected using integral methods that are averaging diagnostic signals. A further difficulty with the processing of gear signals is caused by their cyclostationarity, in particular a relatively long period of recurrence of the signals associated with the kinematics of the gear unit. For a single-stage transmission with \(z_{1}\) pinion teeth and \(z_{2}\) gear teeth, this cycle is repeated every \(z_{1}\) rotation of the wheel and \(z_{2}\) rotation of the pinion shaft. During this time, a damaged pinion tooth comes into contact with all the gear teeth as shown in Fig. 11. On this figure arrows contractually indicate contacts of different tooth pair. Note that the impact of the contact ratio is neglected on this figure. For a gearbox with \(z_1 =27\) and \(z_2 =35\) teeth, rotating with the frequency of \(f_1 =25\,\hbox {Hz}\), the cycle repeats every 1.3 s approximately.

$$\begin{aligned} T_c =\frac{z_2 }{f_1 }=\frac{35}{25\left[ {Hz} \right] }\approx 1.3\left[ s \right] \end{aligned}$$
(1)
Fig. 11
figure 11

The order of cooperation of teeth in a single-stage transmission

Full size image

The observed pinion tooth, being in contact with different wheel teeth, each time generates a slightly different signal (see Figs. 8, 9, 10) resulting from the current conditions of meshing cooperation. In addition, full gear cycle (1) is usually long enough to be able to slightly change the working parameters of the transmission such as the load and rotational frequency. This introduces additional changes to the analyzed signal. All this factors required special methods of signal processing capable of finding in the signal that small nonstationarities that are introduced by the damaged tooth. Figure 11 suggests that separate processing of signal fragments related to the mating of particular tooth pairs may bring new quality into the analysis of gear signals. Particularly it may be possible averaging fragments of signal that are generated by the same tooth pairs.

4.1 Signal segmentation and creation of new observation space

Observation of the simulation results shows that working under specified conditions, each cooperating tooth pair leaves in the signal its specific, repeatable footprint resulting from the dynamics of the gear unit and taking into account current wear, manufacturing and assembly errors, related particularly to:

  • Quality of the gear (precision of surface roughness, pitch errors, etc.),

  • Mounting of geared wheels on the shafts,

  • Quality of workmanship and shafts installation and additional phenomena of bearing and various external factors (e.g., clearances and damage to bearings, vibration of foundations).

Vibroacoustic signal of the full cycle of the gearbox, pictorially shown in Fig. 11, is a periodic signal consisting of the \(z_1 \times z_2 \) pinion/teeth contacts that can be divided into a number of fragments that are repeated cyclically. These are (Fig. 11):

  • Parts of a signal between entering into contact of the consecutive tooth pairs corresponding in length to the circular pitch,

  • Parts of a signal corresponding to the length of the single rotation of the pinion shaft (consisting of the \(z_{1 }\)fragments of the length of circular pitch),

  • Parts of a signal corresponding to the length of the single rotation of the gear shaft (consisting of the \(z_{2 }\)fragments of the length of circular pitch),

  • Full cycle of the gearbox of the length of \(T_{c}\) (1).

Simultaneous recording of the trigger signal on one or both shafts along with the acceleration signal allows the identification of these periodic segments in the signal as they are synchronized with the kinematic of the machine (shafts rotation). It is then possible to synchronously average time signal for the same segments thus reducing randomness of the signal and enhancing differences between segments corresponding to the contacts of the same teeth.

Time signal \(X_{nm} \left( t \right) \) emitted by the selected tooth pair \(\left( {n,m} \right) \) may be treated as a source of information about the quality of contact of this pair. It’s comparison with historical data reveals the trend of signal changes that permits prognosis of the durability of particular tooth pairs of the gearbox. Such reasoning leads to the concept of presentation of the signal or signal parameter changes in the new, Cartesian, observation space of all tooth pairs (n, m) called local mashing plane. On this plane, the places of the disturbances in the signal are thus correlated with the kinematics of the machine. This allows precise location and observation of progressive damage that was earlier unavailable either due to methods of signal processing averaging the signal or because of their too rare occurrence in the signal (once every \(z_1 \cdot z_2 \) contacts, i.e., during the contact of particular pair).

Transformation of the signal into local meshing plane \(\left( {n,m} \right) \) is relatively simple. It requires simultaneous recording of the trigger signal on the single shaft allowing selection of the beginning of shaft rotations. Usage of triggers on both shafts allows additionally setting their initial mutual position relative to each other in case of discontinuities in the signal recording. The recorded signal should be processed as follows:

  • Signal resampling to obtain equal duration of all rotations, calculated as a number of samples. This eliminates disturbances related to the changes of rotation frequency and allows comparing and averaging appropriate signal segments. The experience of the authors indicates that in the case of small fluctuations in the rotational frequency spline interpolation can be used for this purpose. Resampling should provide that the number of samples per one rotation of the pinion shaft should be divisible by the number of pinion teeth resulting in the same length of all segments.

  • Division of the resampled signal into segments of the same length of K samples, corresponding to the time between entering of consecutive pairs into contact. This length corresponds to the duration of the circular pitch and is calculated as a period of a single rotation of the shaft divided by the number of teeth on the gear mounted on this shaft:

    $$\begin{aligned} T=\frac{1}{f_1 z_1 }\left[ s \right] \end{aligned}$$
    (2)

    These segmentation means that with total contact ratio of \(\varepsilon _\gamma >1\), each segment contains only fragment of the whole contact of the tooth pair. Alternatively segment length may be selected to correspond to the expected length of the path of contact, i.e., the average time between entering and exiting from contact. In this case, due to the contact ratio greater than 1, local meshing plane will contain multiplied parts of the signal.

  • The appropriate segments of the signal corresponding to the cooperation of the same tooth pair (n, m) can additionally be averaged to remove the randomness from the signal.

  • All the signal segments can be plotted on a graph in coordinates ,,\(pinion \, teeth \times gear\,teeth\)“ (Fig. 12b).

Note that the local meshing plane constructed in this way is always continuous, within the meaning of the subsequent signal samples, along one of the coordinates (time scale), and discrete along the second coordinate (tooth numbers). This is due to the obvious fact that it is impossible to obtain the mating of all the positions of the teeth to each other, i.e., two tips of the teeth in the normal operation cannot cooperate. Successive signal segments arranged one behind the other on the pinion teeth axis (time axis) for a fixed gear teeth are in reality separated from each other and form a discontinuity at the borders of the segments of the so created time signal (see, e.g., the segments 1 and 2, 11 and 12 in Fig. 12).

Fig. 12
figure 12

Tooth mating in the single-stage gearbox (a) and creation of signal representation on the local meshing plane (b) [39]

Full size image

4.2 Signal analysis on the local meshing plane

The above-presented definition of the local meshing plane transforms the time signal recorded during the operation of the transmission (or its statistical parameters) into the new Cartesian coordinate system ,,\(pinion\,teeth\times gear\,teeth\)“ and allows tabulating of the signal segments related to the cooperation of individual tooth pairs. It introduces new possibilities to the diagnosis of gears allowing evaluation of the quality of cooperation of individual pairs of teeth, which previously was not possible. Tabulating of individual contacts allows, within available hardware resources—especially the controller memory, observation of trends caused by the deterioration of cooperating toothed pairs.

Let’s examine the changes in a squared envelope signal (instantaneous power) of the simulated total meshing force in the presence of pitch errors on pinion and gear previously presented in Fig. 7. Additionally, for a single pinion and wheel teeth, these errors have been enlarged as shown in Fig. 3b. A fragment of the meshing force waveform shown in the lower diagram of Fig. 7 shows the periodic, local increases in the amplitude of the signal caused by these errors wherein the linking of these local disturbances with specific pinion and gear teeth on this basis is impossible. Presentation of this signal on the local meshing plane, shown in Fig. 13, reveals that the major, local, disturbances of the total meshing force are caused by the single pinion and gear teeth (increased amplitude for pinion teeth in the range of 15–19 and gear tooth no. 22). Additionally, increased amplitude could be observed during simultaneous contact of these both, improperly manufactured teeth. This phenomenon is caused by the smaller backlash during this contact but only analysis on the local plane and linking signal disturbances to the particular tooth pair is able to reveal it. Please note that this is relatively rare occurrence, taking place only once for each complete cycle of the gearbox (1). Analyzing signal on the local meshing plane, based on observation of trends in the signal amplitudes along axis of teeth of both wheels, we could obtain information about the quality of meshing of each cooperating tooth pair. We could, therefore, on that basis, indirectly assess the quality of manufacturing of individual teeth, wheels and gear shafts.

Having separate time segments corresponding to all variants of tooth pair contacts, we can compress the diagnostic information by identifying statistical parameters for them. For example, in Fig. 14 maximum values of the instantaneous power of the total meshing force were presented on the local plane. As can be seen, compression of information in this case is 30:1, which results from the assumed length of the segments corresponding to the circular pitch (\(K=30\)). Such compression allows the construction of a diagnostic system that monitors the cooperation of individual tooth pairs by analyzing trends of changes in parameters of signal segments corresponding to their cooperation.

Fig. 13
figure 13

Instantaneous power of the simulated meshing force signal for pitch errors from Fig. 3b (enlarged errors on single pinion and gear tooth)

Full size image
Fig. 14
figure 14

Maximal values of the instantaneous power of the simulated meshing force signal for pitch errors from Fig. 3b (enlarged errors on single pinion and gear tooth)

Full size image

4.3 Envelope contact factor (ECF) on the local meshing plane

As was shown above, envelope analysis may be used for finding local disturbances in the signal caused by the fatigue damages of teeth. In work [40], methodology of diagnosing of such failures was proposed based on the segmentation of the instantaneous power of the signal. It was later developed in the works [38, 39, 41]. Method is based on comparing consecutive segments of the squared envelope of the signal of length associated with the circular pitch. As the signal envelope, in contrary to the measured signal, is a slow changing signal of low sensitivity to phase shift, this allows obtaining proper results of comparison of segments. Using of square envelope additionally increases sensitivity of the method for small changes in the signal. Developed diagnostic parameter called envelope contact factor is a newly created time signal calculated as a point-by-point difference of squared envelopes of consecutive segments associated with the tooth contacts:

$$\begin{aligned} \hbox {ECF}\left( t \right) =\left| {A^{2}\left( {i,t} \right) -A^{2}\left( {i-1,t} \right) } \right| \end{aligned}$$
(3)

where \(i-1\) and i are the number of signal segments. Time symbol t in the equation (3) indicates successive signal samples.

ECF is an energy parameter enhancing changes in tooth contacts resulting from the fluctuations of the meshing force in successive segments of the signal caused by pitch errors, tooth stiffness variations and all the manufacturing inaccuracies of shafts and toothed wheels. Differences in toothed pair meshes result in a increase in dynamic loading of teeth and increase of stress in the tooth base. The biggest variability of this coefficient, the bigger differences exist between tooth contacts.

ECF coefficient, as a differential parameter, is not very sensitive to changes that occur slowly but very well suited for the detection of signals containing changes of impulse type typical for pitting and fatigue tooth crack.

Its calculation is very fast, because ECF can be obtained by cyclically moving the data buffer corresponding to the whole rotation of the shaft of one signal segment (i.e., the first segment becomes final) and subtracting the two buffers apart. Then

$$\begin{aligned} \hbox {ECF}\left( t \right) =\left| {A^{2}\left( {t-\tau } \right) -A^{2}\left( t \right) } \right| \end{aligned}$$
(4)

where \(\tau \) is the time shift corresponding to the circular pitch of the pinion. When calculating ECF in this way, it is not necessary to divide the signal into individual segments. The length of the sample corresponding to the averaged rotation of the shaft should be totally divisible by the number of teeth on this shaft. This means obtaining the same length of all the segments. Since ECF is a continuous function of time, it can be further analyzed by the methods used in the processing of time signals, especially on the aforementioned local meshing plane.

4.4 Local meshing plane in diagnosing tooth crack

During the entire experiment on a back-to-back test stand, the gear vibration acceleration signals were recorded continuously in consecutive blocks with a length of 6 s. Then, the signals corresponding to each rotation of the pinion shaft have been resampled in such a manner that the length of each segment corresponding to circular pitch was of 30 time samples (810 per pinion shaft rotation). Segments assigned to sequentially cooperating tooth pairs were averaged within a single data block, which meant that each segment was averaged about 3/4 times. Numbers of cooperating teeth pinion were followed throughout the experiment to enable continuous numbering of cooperating teeth.

In Fig. 15 instantaneous power of the acceleration signal calculated as its squared envelope (left column) and the ECF (right column) were presented on the local meshing plane for the last part of the experiment. From top to bottom, they correspond to the 60, 62, 65 and 69 min of the experiment that lasted 72 min. Both groups of charts have the same ranges of vertical axis.

Fig. 15
figure 15

Instantaneous power (left) and envelope contact factor (right) changes of the acceleration signal during the experiment on the back-to-back tester

Full size image

Analysis of the instantaneous power of the acceleration signal on the local meshing plane shown in the left column of Fig. 15, in principle, does not show significant changes. Only the last result obtained for about 3 min before the end of the experiment shows a clear increase in the squared envelope signal in the vicinity of the pinion tooth No. 4. At the same time, it is worth noting the increased level of the gear signal around the half of the shaft rotation (gear teeth 15–19). This reflects to the disturbances related to cooperation of the wheel shaft that may be caused for example by manufacturing errors of the wheel (e.g., eccentricity) or the inaccuracy of installation the gear on the shaft. The increase in signal amplitude is greater in the case of operation of these teeth with the pinion teeth starting from No. 4 (4–10). Recalling the results of numerical experiment conducted above, it may be concluded that due to the gradual growth of this phenomenon this is probably caused by the growing damage to the tooth resulting in changes in its rigidity resulting in disturbances in subsequent parts of the signal. These changes, although not visible yet in the signal envelope are enhanced by teeth cooperation inaccuracies and become apparent during contacts of subsequent teeth.

Much more information, as in the case of a instantaneous power analysis, is provided by ECF signal observation on the local plane. Starting at 60 min, its elevated level is visible around the tooth No. 4 cooperating with all gear teeth. In addition, as in the case of a squared envelope, the effect of boosting the ECF ratio due to disturbances introduced by incorrect cooperation of gear teeth around the teeth 15 and 19 is observable. Such a pattern, especially for its earlier absence, indicates the progressive degradation of a single tooth and will usually be attributed to the development of fatigue crack at the tooth base. Other damage, for example, pitting or spalling usually developed on several adjacent teeth will leave at the local meshing plane another, wider signature.

4.5 Remarks on the computational efficiency of presented algorithms

In this paper, the numerical model of the gearbox was used only for the verification of implemented signal processing algorithms and obtaining knowledge about the correlation of meshing processes with the shape of vibroacoustic signal recorded from the gearbox. Therefore, the computational efficiency of this hybrid model composed of FEM models responsible for calculation of meshing stiffness and part responsible for integration of equations of motion will not be discussed here.

Presented algorithms of signal processing are well suited to online data processing in real-time diagnostic systems and could be easily implemented even on the controllers with limited resources. The algorithm responsible for creation of local meshing plane is very fast as it requires only spline interpolation for compensation of different rotation segment lengths and manipulation of thus obtained arrays of samples. Also ECF algorithm, if calculated according to Eq. (4), requires only shifting time data in the array and subtracting it from the original one. One of the problems that requires more computational power is calculation of the signal envelope for energetic operators (e.g., envelope). Obtaining signal’s envelope usually requires lengthy FFT calculations. The squared envelope of the signal could be, however, replaced by the Teager–Kaiser energy operator [42] that has similar effect on the signal and requires just two multiplications and one subtraction for each time sample. Authors were able to continuously perform all calculations related to the ECF on the local meshing plane on one block of data of the length of 6 s, sampled with the frequency of 25.6 kHz, while still waiting for acquiring of another time block.

5 Summary and conclusions

Presented method of local faults detection has been first tested on a simulation model of a single-stage gearbox. The model allows obtaining waveforms, correctly reflecting the actual behavior of the transmission, also in the presence of simulated gear damages such as fatigue damage to the teeth and manufacturing and assembly errors. Model was used to explain the phenomena that affect the way the vibroacoustic signal is generated by cooperating tooth pairs. It also explains the effect of the type and amount of damage of the teeth on the formation of local, low-energy, signal disturbances. The use of a simulation model makes possible to investigate the correlation between the location of local disturbances in the signal, kinematics of the gearbox and dynamics of the gear unit. As was shown by simulations, observation of the places of entering and leaving of tooth pairs from contact in the signal is particularly informative regarding the appearance of the early phases of the development of damage gear pairs.

Methods of signal processing used in the paper are based on signal segmentation in time domain. Segmentation of the signal allows presenting results on the so-called local meshing plane, a plane in Cartesian coordinates pinion teeth versus gear teeth. Signal representation on this plane allows to link local nonstationarities in the signal to the relative positions of both shafts (particular teeth) so that the visible changes in the signal are directly linked to the tooth local fatigue damages such as pitting and tooth base fracture as well as manufacturing errors (e.g., pitch errors, imbalance or misalignment of shafts) in gearbox. Although presented methods of signal processing on the local plane are based on instantaneous power of the signal (signal’s envelope), other time signal processing methods may also be used in this purpose (e.g., Teager–Kaiser energy operator).

The effectiveness of the developed methods was confirmed in a diagnostic experiments carried out on a back-to-back test stand.

Analysis of vibroacoustic signal of gear on the local meshing plane can complement the procedures for assessment of technical condition of gear both at the stage of assessing its quality during the technical acceptances as well as during normal operation. This observation at the stage of final quality control in production will allow to detect inaccuracy of individual parts and to assess the quality of their final assembly. Importantly, such an assessment can be made during normal transmission operation allowing you to detect potential sources of increased vibration or noise.