A boundary modulation formulation for cable’s non-planar coupled dynamics under out-of-plane support motion

Abstract

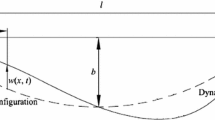
Suspended cable’s non-planar resonant coupled dynamics under out-of-plane support motion is investigated by the multiple- scale method, with a boundary modulation formulation established and nonlinear dynamic responses analyzed. Explicitly, to cope with the difficulty due to moving boundary, the small resonant support motion is properly rescaled and incorporated into cable’s modulation equations as a boundary resonant modulation term, through constructing solvability conditions of the multi-scale expansions. And the boundary resonance dynamic coefficient, characterizing the boundary modulation effect, is derived analytically for cable’s two-to-one resonant coupled dynamics. Numerical results for cable’s non-planar coupled dynamic responses, including stability and bifurcation analysis for the equilibrium solutions of modulation equations, are obtained and presented in the end, with both saddle-node bifurcations and Hopf bifurcations detected.

Appendix

Suspended cable’s linear modal analysis can be found in reference [3]. The in-plane symmetric modes are given by

$$\begin{aligned} \phi _n \left( x \right) =c_n \left[ {1-\tan \left( {\frac{ \omega _n^{\left( \mathrm{in} \right) } }{2}} \right) \sin \omega _n^{\left( \mathrm{in} \right) } x-\cos \omega _n^{\left( \mathrm{in} \right) } x} \right] ,\quad n=1,3,5\ldots \end{aligned}$$

(40)

where $c_{i}$ is the normalization constants. And the associated eigenfrequencies are determined by

$$\begin{aligned} \frac{1}{2}\omega _n^{\left( \mathrm{in} \right) } -\tan \left( {\frac{1}{2}\omega _n^{\left( \mathrm{in} \right) } } \right) -\frac{1}{2\lambda ^{2}}\left( {\omega _n^{\left( \mathrm{in} \right) } } \right) ^{3}=0,\quad n=1,3,5\ldots \end{aligned}$$

(41)

where $\lambda ^{2}={EA}/{mgl}(8b/l)^{3}$ is the elasto-geometric parameter. The above nonlinear transcendental equations can be solved by the Newton–Raphson method.

The in-plane antisymmetric modes are

$$\begin{aligned} \phi _n \left( x \right) =\sqrt{2}\sin \left( {n\pi x} \right) ,\quad n=2,4,6\ldots \end{aligned}$$

(42)

with the associated eigenfrequencies as

$$\begin{aligned} \omega _n^{\left( \mathrm{in} \right) } =n\pi ,\quad n=2,4,6\ldots \end{aligned}$$

(43)

And the out-of-plane modes are

$$\begin{aligned} \varphi _m \left( x \right) =\sqrt{2}\sin \left( {m\pi x} \right) ,\quad m=1,2,3,\ldots \end{aligned}$$

(44)

with the associated eigenfrequencies as

$$\begin{aligned} \omega _m^{\left( \mathrm{out} \right) } =m\pi ,\quad m=1,2,3\ldots \end{aligned}$$

(45)