Skip to main content
SpringerLink
Log in

Buckling of cylindrical shell panels: a MAEM solution

  • Special
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

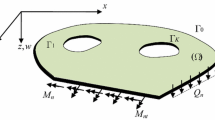
The meshless analog equation method, a purely mesh-free method, is applied to the buckling analysis of cylindrical shell panels. The method is based on the principle of the analog equation, which converts the three governing partial differential equations in terms of displacements into three uncoupled substitute equations, two Poisson’s equations and one plate equation, under fictitious sources. The fictitious sources are represented by series of radial basis functions (RBFs) of multiquadric type, and the substitute equations are integrated. This integration allows the representation of the sought solution by new RBFs, which approximate accurately not only the displacements but also their derivatives involved in the governing equations. Then, by inserting the approximate solution in the original differential equations and the associated boundary conditions and collocating at a predefined set of mesh-free nodal points, a linear algebraic eigenvalue problem results, the solution of which gives the buckling loads and modes. The optimal value of the shape parameter of the RBFs is obtained as that minimizing eigenvalues. The method is illustrated by analyzing several shell panels. The studied examples demonstrate the efficiency and the accuracy of the presented method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Timoshenko S., Gere J.M.: Theory of Elastic Stability, 2nd edn. McGraw-Hill, New York (1961)

    Google Scholar 

  2. Flügge W.: Stresses in Shells. Springer, Berlin (1962)

    Google Scholar 

  3. Brush D.O., Almroth B.O.: Buckling of Bars, Plates and Shells. McGraw-Hill, New York (1975)

    MATH  Google Scholar 

  4. Gerard, G., Becker, H.: Handbook of Structural Stability Part III-Buckling of Curved Plates and Shells. NACA TN 3783, Washington (1975)

  5. Bushnell D.: Computerized Buckling Analysis of Shells. Martinus Nijhoff Publishers, Dordrecht (1985)

    Book  Google Scholar 

  6. Zhang J.D., Atluri S.N.: Post-buckling analysis of shallow shells by the field-boundary element method. Int. J. Numer. Methods Eng. 26, 571–587 (1986)

    Article  Google Scholar 

  7. Baiz P.M., Aliabadi M.H.: Linear buckling analysis of shear deformable shallow shells by the domain boundary element method. Comput. Model. Eng. Sci. 13(1), 19–34 (2006)

    MathSciNet  Google Scholar 

  8. Baiz P.M., Aliabadi M.H.: Buckling analysis of shear deformable shallow shells by the boundary element method. Eng. Anal. Bound. Elem. 31, 361–372 (2007)

    Article  MATH  Google Scholar 

  9. Katsikadelis, J.T., Yiotis, A.J: Linear buckling analysis of cylindrical shell panels using BEM. In: Proceedings of the 8th HSTAM International Congress on Mechanics, vol. II, pp. 889–896. Patras, Greece (2007)

  10. Cheng A.H.D, Golbeg M.A., Kansa E.J., Zammito G.: Exponential convergence and h-c multiquadric collocation method for partial differential equations. Numer. Methods Partial Differ. Equ. 19(5), 571–594 (2003)

    Article  MATH  Google Scholar 

  11. Kansa E.J.: Highly accurate methods for solving elliptic partial differential equations. In: Brebbia, C.A., Divo, E., Poljak, D. (eds.) Boundary Elements XXVII, pp. 5–15. WIT Press, Southampton (2005)

    Google Scholar 

  12. Ferreira A.J.M., Roque C.M.C., Jorge R.M.M.: Static and free vibration analysis of composite shells by radial basis functions. Eng. Anal. Bound. Elem. 30, 719–733 (2006)

    Article  MATH  Google Scholar 

  13. Ferreira A.J.M., Roque C.M.C., Jorge R.M.M.: Modelling cross-ply laminated elastic shells by a higher-order theory and multiquadrics. Comput. Struct. 84, 1288–1299 (2006)

    Article  Google Scholar 

  14. Katsikadelis J.T.: The meshless analog equation method. A new highly accurate truly mesh-free method for solving partial differential equations. In: Brebbia, C.A., Katsikadelis, J.T. (eds.) Boundary Elements and other mesh reduction methods XXVIII, pp. 13–22. WIT Press, Southampton (2006)

    Chapter  Google Scholar 

  15. Katsikadelis J.T.: The 2D elastostatic problem in inhomogeneous anisotropic bodies by the meshless analog equation method MAEM. Eng. Anal. Bound. Elem. 32, 997–1005 (2008). doi:10.1016/j.enganabound.2007.10.016

    Article  MATH  Google Scholar 

  16. Katsikadelis J.T.: A generalized Ritz method for partial differential equations in domains of arbitrary geometry using global shape functions. Eng. Anal. Bound. Elem. 32(5), 353–367 (2008). doi:10.1016/j.enganabound.2007.001

    Article  MATH  Google Scholar 

  17. Yiotis, A.J., Katsikadelis, J.T.: The meshless analog equation method for the solution of plate problems. In: Proceedings of the 6th GRACM International Congress on Computational Mechanics, Thessaloniki, Greece (2008)

  18. Katsikadelis J.T.: The meshless analog equation method: I. Solution of elliptic partial differential equations. Arch. Appl. Mech. 79, 557–578 (2009)

    Article  MATH  Google Scholar 

  19. Jang S.K., Bert C.W., Bert C.W., Bert C.W.: Application of differential quadrature to static analysis of structural components. Int. J. Numer. Methods Eng. 28(3), 561–577 (1989)

    Article  MATH  Google Scholar 

  20. Katsikadelis, J.T., Platanidi, J.G.: 3D analysis of thick shells by the meshless analog equation method. In: Proceedings of the 1st International Congress of Serbian Society of Mechanics, pp. 475–484 (2007)

  21. Yiotis A.J., Katsikadelis J.T.: Analysis of cylindrical shell panels. A meshless solution. Eng. Anal. Bound. Elem. 37, 928–935 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  22. Budiansky B.: Notes on nonlinear shell theory. J. Appl. Mech. 35, 329–401 (1968)

    Article  Google Scholar 

  23. Kraus H.: Thin Elastic Shells. An Introduction to the Theoretical Foundations and the Analysis of Their Static and Dynamic Behabior. Wiley, New York (1967)

    Google Scholar 

  24. Leissa A.W.: Vibrations of Shells. Scientific and Technical Information Office, NASA, Washington (1973)

    Google Scholar 

  25. Katsikadelis J.T.: The analog equation method. A boundary-only integral equation method for nonlinear static and dynamic problems in general bodies. Int. J. Theor. Appl. Mech. Arch. Appl. Mech. 27, 13–38 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  26. Ferreira A.J.M., Roque C.M.C., Martins P.A.L.S.: Analysis of thin isotropic rectangular and circular plates with multiquadrics. Strength Mater. 37(2), 163–173 (2005)

    Article  Google Scholar 

  27. Sarra S.A.: Integrated multiquadric radial basis function methods. Comput. Math. Appl. 51, 1283–1296 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  28. Yao G., Tsai C.H., Chen W.: The comparison of three meshless methods using radial basis functions for solving fourth-order partial differential equations. Eng. Anal. Bound. Elem. 34, 625–631 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  29. Hardy R.L.: Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 76, 1905–1915 (1971)

    Article  Google Scholar 

  30. Franke R.: Scattered data interpolation: tests of some methods. Math. Comput. 38(157), 181–200 (1982)

    MATH  MathSciNet  Google Scholar 

  31. Foley T.A.: Near optimal parameter selection for multiquadric interpolation. J. Appl. Sci. Comput. 1, 54–69 (1994)

    MathSciNet  Google Scholar 

  32. Rippa S.: An algorithm for selecting a good value for the parameter c in radial basis function approximation. Adv. Comput. Math. 11, 193–210 (1999)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, National Technical University of Athens, Athens, Greece

    Aristophanes J. Yiotis & John T. Katsikadelis

Authors
  1. Aristophanes J. Yiotis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John T. Katsikadelis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aristophanes J. Yiotis.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yiotis, A.J., Katsikadelis, J.T. Buckling of cylindrical shell panels: a MAEM solution. Arch Appl Mech 85, 1545–1557 (2015). https://doi.org/10.1007/s00419-014-0944-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-014-0944-9

Keywords

Search

Navigation