Skip to main content
SpringerLink
Log in

Closed-form solutions for stepped Timoshenko beams with internal singularities and along-axis external supports

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

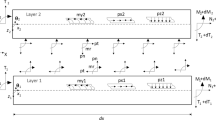
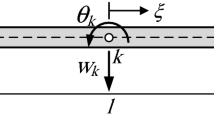
The Timoshenko beam model in presence of internal singularities causing deflection and rotation discontinuities and resting on external concentrated supports along the span is studied in a static context. The internal singularities are modelled as concentrated reductions in the flexural and the shear stiffness by making use of the distribution theory. Along-axis supports are treated as unknown concentrated loads and moments. An exact integration procedure of the proposed model, not requiring continuity conditions at all, is presented. Closed-form solutions are provided for both cases of homogeneous and stepped Timoshenko beams. The so-called static Green’s functions are also obtained by the proposed procedure and their explicit expressions are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Paipetis S.A., Dimarogonas A.D.: Analytical Methods in Rotor Dynamics. Elsevier Applied Science, London (1986)

    Google Scholar 

  2. Rizos P.F., Aspragathos N., Dimarogonas A.D.: Identification of crack location and magnitude in a cantilever beam from the vibration modes. J Sound Vib 138(3), 381–388 (1990)

    Article  Google Scholar 

  3. Koplow M.A., Bhattacharyya A., Mann B.P.: Closed form solutions for the dynamic response of Euler–Bernoulli beams with step changes in cross section. J Sound Vib 295(1–2), 214–225 (2006)

    Article  Google Scholar 

  4. Kanwal R.P.: Generalised Functions Theory and Applications. Academic Press, New York (1983)

    Google Scholar 

  5. Yavari A., Sarkani S., Moyer E.T.: On applications of generalised functions to beam bending problems. Int. J. Solids Struct. 37, 5675–5705 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  6. Yavari A., Sarkani S.: On applications of generalized functions to the analysis of Euler–Bernoulli beam-columns with jump discontinuities. Int. J. Mech. Sci. 43(6), 1543–1562 (2001)

    Article  MATH  Google Scholar 

  7. Khiem N.T., Lien T.V.: A simplified method for natural frequency analysis of a multiple cracked beam. J. Sound Vib. 245(4), 737–751 (2001)

    Article  Google Scholar 

  8. Li Q.S.: Free vibration analysis of non-uniform beams with an arbitrary number of cracks and concentrated masses. J. Sound Vib. 252(3), 509–525 (2002)

    Article  Google Scholar 

  9. Wang J., Qiao P.: Vibration of beams with arbitrary discontinuities and boundary conditions. J. Sound Vib. 308, 12–27 (2007)

    Article  Google Scholar 

  10. Biondi B., Caddemi S.: Closed form solutions of Euler–Bernoulli beams with singularities. Int. J. Solids Struct. 42, 3027–3044 (2005)

    Article  MATH  Google Scholar 

  11. Biondi B., Caddemi S.: Euler–Bernoulli beams with multiple singularities in the flexural stiffness. Eur. J. Mech. A/Solids 26(5), 789–809 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  12. Caddemi S., Caliò I.: Exact closed-form solution for the vibration modes of the Euler–Bernoulli beam with multiple open cracks. J. Sound Vib. 327(3–5), 473–489 (2009)

    Article  Google Scholar 

  13. Caddemi S., Caliò I.: Exact solution of the multi-cracked Euler–Bernoulli column. Int. J. Solids Struct. 45(16), 1332–1351 (2008)

    Article  MATH  Google Scholar 

  14. Caddemi S., Caliò I.: The influence of the axial force on the vibration of the Euler–Bernoulli beam with an arbitrary number of cracks. Arch. Appl. Mechanics. 82(6), 827–839 (2012)

    Article  Google Scholar 

  15. Palmeri A., Cicirello A.: Physically-based Dirac’s delta functions in the static analysis of multi-cracked Euler–Bernoulli and Timoshenko beams. Int. J. Solids Struct. 48, 2184–2195 (2011)

    Article  Google Scholar 

  16. Failla G., Santini A.: On Euler–Bernoulli discontinuous beam solutions via uniform-beam Green’s functions. Int. J. Solids Struct. 44(22–23), 7666–7687 (2007)

    Article  MATH  Google Scholar 

  17. Failla G., Santini A.: A solution method for Euler–Bernoulli vibrating discontinuous beams. Mech. Res. Commun. 35(8), 517–529 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  18. Failla G.: Closed-form solutions for Euler–Bernoulli arbitrary discontinuous beams. Arch. Appl. Mech. 81, 605–628 (2011)

    Article  Google Scholar 

  19. Timoshenko S.P., Gere J.M.: Theory of Elastic Stability. McGraw-Hill, New York (1961)

    Google Scholar 

  20. Lighthill M.J.: An Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press, London (1958)

    Book  Google Scholar 

  21. Guelfand I.M., Chilov G.E.: Les Distribution. Dunod, Paris (1972)

    Google Scholar 

  22. Hoskins R.F.: Generalised Functions. Ellis Horwood Limited, Chichester (1979)

    MATH  Google Scholar 

  23. Zemanian A.H.: Distribution Theory and Transform Analysis. McGraw-Hill, New York (1965)

    MATH  Google Scholar 

  24. Bagarello F.: Multiplication of distribution in one dimension and a first application to quantum field theory. J. Math. Anal. Appl. 266, 298–320 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  25. Calió. I., Elishakoff I.: Closed-form solutions for axially graded beam-columns. J. Sound Vib. 280(3–5), 1083–1094 (2005)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Ingegneria Civile e Ambientale, Università degli Studi di Catania, Viale Andrea Doria 6, 95125, Catania, Italy

    S. Caddemi, I. Caliò & F. Cannizzaro

Authors
  1. S. Caddemi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Caliò
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. Cannizzaro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Caddemi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Caddemi, S., Caliò, I. & Cannizzaro, F. Closed-form solutions for stepped Timoshenko beams with internal singularities and along-axis external supports. Arch Appl Mech 83, 559–577 (2013). https://doi.org/10.1007/s00419-012-0704-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-012-0704-7

Keywords

Search

Navigation