Skip to main content
SpringerLink
Log in

Approximate analysis of progressive deformation in honeycomb structures subjected to in-plane loading

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

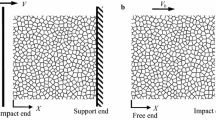
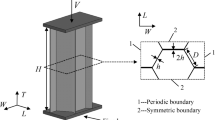
Progressive deformation of honeycomb structures subjected to in-plane loading was approximately analyzed by using the collapse modes of hexagonal unit cells. The collapse modes were categorized as freely compressive, restricted compressive, and shear. Moreover, there were five characteristic deformation patterns, namely deformation bands. Average stresses of the collapsing honeycomb models were evaluated in terms of the plastic collapse stress per hinge and total number of hinges of progressively arising deformation bands. The displacements of the models were obtained by multiplying the displacement per cell with the number of collapsed cells. The present method was used to analyze progressive deformation of typical honeycomb structures. The validity of the stress–displacement relations derived for some structures was confirmed by comparing them with finite element method (FEM) results. Our method is much simpler than FEM but just as effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gibson L.J., Ashby M.F., Schajer G.S., Robertson C.I.: Mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 382, 25–42 (1982)

    Article  Google Scholar 

  2. Gibson L.J., Ashby M.F.: Cellular solids: structure and properties, 2nd edn, pp. 93–174. Cambridge University Press, Cambridge (1997)

    Google Scholar 

  3. Andrews E.W., Gibson L.J., Ashby M.F.: The creep of cellular solids. Acta Mater. 47, 2853–2863 (1999)

    Article  Google Scholar 

  4. Masters I.G., Evans K.E.: Models for the elastic deformation of honeycombs. Compos. Struct. 35, 403–422 (1996)

    Article  Google Scholar 

  5. Papka S.D., Kyriakides S.: In-plane compressive response and crushing of honeycombs. J. Mech. Phys. Solids 42, 1499–1532 (1994)

    Article  Google Scholar 

  6. Papka S.D., Kyriakides S.: Experiments and full-scale numerical simulations of in-plane crushing of a honeycomb. Acta Mater. 46, 2765–2776 (1998)

    Article  Google Scholar 

  7. Zhu H.X., Mills N.J.: The in-plane non-linear compression of regular honeycombs. Int. J. Solids Struct. 37, 1931–1949 (2000)

    Article  MATH  Google Scholar 

  8. Hönig A., Stronge W.J.: In-plane dynamic crushing of honeycomb. Part I: crush band initiation and wave trapping. Int. J. Mech. Sci. 44, 1665–1696 (2002)

    Article  MATH  Google Scholar 

  9. Hönig A., Stronge W.J.: In-plane dynamic crushing of honeycomb. Part II: application to impact. Int. J. Mech. Sci. 44, 1697–1714 (2002)

    Article  MATH  Google Scholar 

  10. Ruan D., Lu G., Wang B., Yu T.X.: In-plane dynamic crushing of honeycombs—a finite element study. Int. J. Impact Eng. 28, 161–182 (2003)

    Article  Google Scholar 

  11. Nakamoto H., Adachi T., Araki W.: In-plane impact behavior of honeycomb structures randomly filled with rigid inclusions. Int. J. Impact Eng. 36, 73–80 (2009)

    Article  Google Scholar 

  12. Nakamoto H., Adachi T., Araki W.: In-Plane Impact behavior of honeycomb structures filled with linearly arranged inclusions. Int. J. Impact Eng. 36, 1019–1026 (2009)

    Article  Google Scholar 

  13. Ohno N., Okumura D., Noguchi H.: Microscopic symmetric bifurcation condition of cellular solids based on a homogenization theory of finite deformation. J. Mech. Phys. Solids 50, 1125–1153 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  14. Okumura D., Ohno N., Noguchi H.: Elastplastic microscopic bifurcation and post-bifurcation behavior of periodic cellular solids. J. Mech. Phys. Solids 52, 641–666 (2004)

    Article  MATH  Google Scholar 

  15. Hutzler S., Weaire D.: Buckling properties of 2D regular elastomeric honeycombs. J. Phys. Condens. Matter 9, L323–L329 (1997)

    Article  Google Scholar 

  16. Jagla E.A.: The buckling transition of two-dimensional elastic honeycombs: numerical simulation and Landau theory. J. Phys. Condens. Matter 16, 4419–4428 (2004)

    Article  Google Scholar 

  17. Karagiozova D., Yu T.X.: Plastic deformation modes of regular hexagonal honeycombs under in-plane biaxial compression. Int. J. Mech. Sci. 46, 1489–1515 (2004)

    Article  MATH  Google Scholar 

  18. Li K., Gao X.L., Wang J.: Dynamic crushing behavior of honeycomb structures with irregular cell shapes and non-uniform cell wall thickness. Int. J. Solids Struct. 44, 5003–5026 (2007)

    Article  MATH  Google Scholar 

  19. Noor A.K.: Computational structures technology: leap frogging into the twenty-first century. Comput. Struct. 73, 1–31 (1999)

    Article  MATH  Google Scholar 

  20. Al Galib D., Limam A.: Experimental and numerical investigation of static and dynamic axial crushing of circular aluminum tubes. Thin-Walled Struct. 42, 1103–1137 (2004)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Technology Development Department, Ebara Corporation, 4-2-1 Honfujisawa, Fujisawa-shi, 251-8502, Japan

    Hiroaki Nakamoto

  2. Department of Mechanical Engineering, Toyohashi University of Technology, 1-1 Hibarigaoka, Tempaku, Toyohashi, 441-8580, Japan

    Tadaharu Adachi & Masahiro Higuchi

Authors
  1. Hiroaki Nakamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tadaharu Adachi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Masahiro Higuchi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tadaharu Adachi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nakamoto, H., Adachi, T. & Higuchi, M. Approximate analysis of progressive deformation in honeycomb structures subjected to in-plane loading. Arch Appl Mech 83, 379–396 (2013). https://doi.org/10.1007/s00419-012-0685-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-012-0685-6

Keywords

Search

Navigation