Skip to main content
SpringerLink
Log in

Interfacial fracture analysis of a graded piezoelectric layer on a substrate with finite dimension

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

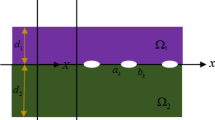
Abstract

In fracture analysis of piezoelectric devices, the structural dimension is often assumed to be infinite at least in one direction. However, all practical piezoelectric structures are finite and their dimensions in different directions are often comparable and cannot be simplified as infinite. The assumption of infinite dimension may lead to inexact theoretical results. The present work aims at studying the interfacial fracture behavior of a functionally graded piezoelectric layer on a dielectric substrate with finite dimension. The crack problem is solved by the methods of Fourier series and Cauchy singular integral equation. Parametric studies on the stress intensity factor (SIF) reveal the following: (a) when a crack tip is near to an interface end, its SIF is mainly governed by the end effect; (b) when a crack is far from the interface ends and the piezoelectric layer is thin, its SIF is principally affected by the thickness of the piezoelectric layer, and (c) only when a crack is far from the interface ends and meanwhile the piezoelectric layer is thick will its SIF be dominated by the non-homogeneity parameter, and in this case, the SIF increases with the increasing non-homogeneity parameter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zimmermann C., Rebiere D., Dejous C., Pistre J., Chastain E., Planade R.: A Love wave gas sensor coated with functionalized polysiloxane for sensing organophosphorus compounds. Sens. Actuators B 76, 88–94 (2001)

    Google Scholar 

  2. Li Y.D., Lee K.Y.: Dynamic responses of a crack in a layered graded magnetoelectroelastic sensor subjected to harmonic waves. Acta Mech. 204, 217–234 (2009)

    Article  MATH  Google Scholar 

  3. Wang X.Y., Yu S.W.: Transient response of a crack in piezoelectric strip subjected to the mechanical and electrical impacts: mode-III problem. Int. J. Solid. Struct. 37, 5795–5808 (2000)

    Article  MATH  Google Scholar 

  4. Li X.F., Lee K.Y.: Electroelastic behavior of a rectangular piezoelectric ceramic with an antiplane shear crack at arbitrary position. Euro. J. Mech. A/Solid. 23, 645–658 (2004)

    Article  MATH  Google Scholar 

  5. Parton V.Z.: Fracture mechanics of piezoelectric materials. Acta Astronaut. 3, 671–683 (1976)

    Article  MATH  Google Scholar 

  6. Suo Z., Kuo C.M., Barnett D.M., Willis J.R.: Fracture mechanics for piezoelectric ceramics. J. Mech. Phys. Solid. 40, 739–765 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  7. Hao T.H., Shen Z.Y.: A new electric boundary condition of electric fracture mechanics and its applications. Eng. Fract. Mech. 47, 793–802 (1994)

    Article  Google Scholar 

  8. Zhou Z.G., Wang B.: Two parallel symmetry permeable cracks in functionally graded piezoelectric/piezomagnetic materials under anti-plane shear loading. Int. J. Solid. Struct. 41, 4407–4422 (2004)

    Article  MATH  Google Scholar 

  9. Wang B.L., Mai Y.W.: Impermeable crack and permeable crack assumptions, which one is more realistic?. J. Appl. Mech. 71, 575–578 (2004)

    Article  MATH  Google Scholar 

  10. Zhou Z.G., Wang B.: The behavior of two parallel symmetry permeable interface cracks in a piezoelectric layer bonded to two half piezoelectric materials planes. Int. J. Solid. Struct. 39, 4485–4500 (2002)

    Article  MATH  Google Scholar 

  11. Zhang T.Y., Tong P.: Fracture mechanics for a mode III crack in a piezoelectric material. Int. J. Solid. Struct. 33, 343–359 (1996)

    Article  MATH  Google Scholar 

  12. Park S., Sun C.T.: Fracture criteria for piezoelectric ceramics. J. Am. Ceram. Soc. 78, 1475–1480 (1995)

    Article  Google Scholar 

  13. Zuo J.Z., Sih G.C.: Energy density theory formulation and interpretation of cracking behavior for piezoelectric ceramics. Theor. Appl. Fract. Mech. 34, 17–33 (2000)

    Article  Google Scholar 

  14. Feng W.J., Su R.K.L.: Dynamic internal crack problem of a functionally graded magneto-electro-elastic strip. Int. J. Solid. Struct. 43, 5196–5216 (2006)

    Article  MATH  Google Scholar 

  15. Shin J.W., Lee K.Y.: Eccentric crack in a piezoelectric strip bonded to half planes. Euro. J. Mech. A/Solid. 19, 989–997 (2000)

    Article  MATH  Google Scholar 

  16. Li Y.D., Lee K.Y.: Fracture analysis and improved design for a symmetrically bonded smart structure with linearly non-homogeneous magnetoelectroelastic properties. Eng. Fract. Mech. 75, 3161–3172 (2008)

    Article  Google Scholar 

  17. Li Y.D., Lee K.Y.: Anti-plane crack intersecting the interface in a bonded smart structure with graded magnetoelectroelastic properties. Theor. Appl. Fract. Mech. 50, 235–242 (2008)

    Article  Google Scholar 

  18. Li Y.D., Lee K.Y.: Anti-plane fracture analysis for the weak-discontinuous interface in a non-homogeneous piezoelectric bi-material structure. Euro. J. Mech. A/Solid. 28, 241–247 (2009)

    Article  MATH  Google Scholar 

  19. Li Y.D., Lee K.Y.: Interaction between an electrically permeable crack and the imperfect interface in a functionally graded piezoelectric sensor. Int. J. Eng. Sci. 47, 363–371 (2009)

    Article  MathSciNet  Google Scholar 

  20. Li X.F., Xu L.R.: Transient response of a finite bimaterial plate containing a crack perpendicular to and terminating at the interface. J. Appl. Mech. 73, 544–554 (2006)

    Article  MATH  Google Scholar 

  21. Li X.F., Duan X.Y.: An interfacially-cracked orthotropic rectangular bi-material subjected to antiplane shear loading. Appl. Math. Comput. 174, 1060–1079 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Li X.F., Guo S.H.: Effects of nonhomogeneity on dynamic stress intensity factors for an antiplane interface crack in a functionally graded material bonded to an elastic semi-strip. Comput. Mater. Sci. 38, 432–441 (2006)

    Article  Google Scholar 

  23. Gradshteyn I.S., Ryzhik I.M.: Table of Integrals, Series and Products. Academic Press, New York (1980)

    MATH  Google Scholar 

  24. Li Y.D., Lee K.Y.: Fracture analysis on the arc-shaped interface in a layered cylindrical piezoelectric sensor polarized along its axis. Eng. Fract. Mech. 76, 2065–2073 (2009)

    Article  Google Scholar 

  25. Erdogan F., Gupta G.D.: On the numerical solution of singular integral equations. Quart. Appl. Math. 29, 525–534 (1972)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Academy of Armored Force Engineering, No. 21, Du Jia Kan, Chang Xin Dian, 100072, Beijing, People’s Republic of China

    Yong-Dong Li

  2. School of Mechanical Engineering, Yonsei University, Seoul, 120-749, Republic of Korea

    Yong-Dong Li & Kang Yong Lee

Authors
  1. Yong-Dong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kang Yong Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kang Yong Lee.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, YD., Lee, K.Y. Interfacial fracture analysis of a graded piezoelectric layer on a substrate with finite dimension. Arch Appl Mech 80, 1007–1016 (2010). https://doi.org/10.1007/s00419-009-0356-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-009-0356-4

Keywords

Search

Navigation