Abstract
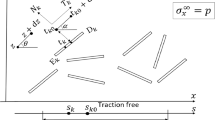
The elastostatic plane problem of an infinite elastic layer with an internal crack is considered. The elastic layer is subjected to two different loadings, (a) the elastic layer is loaded by a symmetric transverse pair of compressive concentrated forces P/2, (b) it is loaded by a symmetric transverse pair of tensile concentrated forces P/2. The crack is opened by an uniform internal pressure p 0 along its surface and located halfway between and parallel to the surfaces of the elastic layer. It is assumed that the effect of the gravity force is neglected. Using an appropriate integral transform technique, the mixed boundary value problem is reduced to a singular integral equation. The singular integral equation is solved numerically by making use of an appropriate Gauss–Chebyshev integration formula and the stress-intensity factors and the crack opening displacements are determined according to two different loading cases for various dimensionless quantities.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bogy D.B.: The plane elastostatic solution for a symmetrically loaded crack in a strip composite. Int. J. Eng. Sci. 11, 985–996 (1973)
Delale F., Erdogan F.: The crack problem for a nonhomogeneous plane. J. Appl. Mech. 50, 609–614 (1983)
Delale F., Erdogan F.: Interface crack in a nonhomogeneous elastic medium. Int. J. Eng. Sci. 26(6), 559–568 (1988)
Erdogan F., Gupta G.D.: The stress analysis of multi-layered composites with a flaw. Int. J. Solids Struct. 7, 39–61 (1971)
Erdogan F., Gupta G.D.: Layered composites with an interface flaw. Int. J. Solids Struct. 7, 1089–1107 (1971)
Erdogan F., Gupta G.D.: On the numerical solution of singular integral equations. Q. Appl. Math. 30, 533–547 (1972)
Gecit M.R.: A cracked elastic strip bonded to a rigid support. Int. J. Fract. 14(6), 575–583 (1978)
Gecit M.R.: Fracture of a surface layer bonded to a half space. Int. J. Eng. Sci. 17, 287–295 (1979)
Gupta G.D.: A layered composite with a broken laminate. Int. J. Solids Struct. 9, 1141–1154 (1973)
Gupta G.D., Erdogan F.: The problem of edge cracks in an infinite strip. J. Appl. Mech. 41, 1001–1006 (1974)
Krenk S.: On the elastic strip with an internal crack. Int. J. Solids Struct. 11, 693–708 (1975)
Krenk S., Bakioglu M.: Transverse cracks in a strip with reinforced surfaces. Int. J. Fract. 11(3), 441–447 (1975)
Krenk S.: A note on the use of the interpolation polynomial for solutions of singular integral equations. Q. Appl. Math. 32, 479–485 (1975)
Ma C.C., Luo J.J.: Plane solutions of interface cracks in anisotropic dissimilar media. J. Eng. Mech. 122(1), 30–38 (1996)
Matysiak S.J., Pauk V.J.: On crack problem in an elastic ponderable layer. Int. J. Fract. 96, 371–380 (1999)
Matysiak S.J., Pauk V.J.: Edge crack in an elastic layer resting on a Winkler foundation. Eng. Fract. Mech. 70, 2353–2361 (2003)
Nied H.F., Erdogan F.: A cracked beam or plate transversely loaded by a stamp. Int. J. Solids Struct. 15, 951–965 (1979)
Ozturk M., Erdogan F.: Axisymmetric crack problem in bonded materials with a graded interfacial region. Int. J. Solids Struct. 33(2), 193–219 (1996)
Zhao Z.G., Zhang X.W., Bai Y.Y.: Investigation of two Griffith cracks subjected to uniform tension by using the non-local theory. Int. J. Eng. Sci. 37, 1709–1722 (1999)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Birinci, A., Birinci, F., Cakiroglu, F.L. et al. An internal crack problem for an infinite elastic layer. Arch Appl Mech 80, 997–1005 (2010). https://doi.org/10.1007/s00419-009-0355-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-009-0355-5