Before the end of an error: Giovanni Bianchini’s original flawed treatise on the conversion of stellar coordinates

Abstract

In my 2018 article in this journal, I described 15th-century Italian astronomer Giovanni Bianchini’s treatment of the problem of stellar coordinate conversion in his Tabulae primi mobilis, the first correct European solution. In this treatise Bianchini refers to a book he had written previously, containing the same error that had plagued his predecessors’ work on the problem. In this article, we announce the discovery of this earlier treatise. We compare its canons and tables to Bianchini’s later work, noting the places where the contents overlap (roughly one quarter of the text). We analyze his mathematical methods and the unique tables he constructed for converting stellar coordinates, including the earliest known European arc sine table, that he would abandon only a few years later.

1 Introduction

In my 2018 paper in this journal, “The end of an error: Bianchini, Regiomontanus, and the tabulation of stellar coordinates”,¹ I discussed the spherical astronomy of Giovanni Bianchini, a mid-15th century administrator and astrologer in Ferrara. His text on the subject, the Tabulae primi mobilis, consists of 52 chapters of canons averaging a little less than a page each, and about 100 pages of numerical tables. This work breaks from its predecessors in Alfonsine astronomy in a number of ways. If one were to identify a single theme that characterizes its numerous contributions, it would be the introduction of stellar and planetary latitudes into spherical astronomy and astrology.

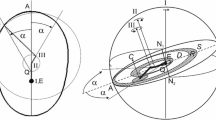
My previous paper dealt with Bianchini’s correction of a centuries-old error in the conversion of stellar coordinates. In Ptolemaic astronomy, positions of planets were determined using the ecliptic as the reference circle: longitudes $\lambda$ were measured along the ecliptic from the vernal equinox $\Upsilon$, and latitudes $\beta$ were measured at right angles to the ecliptic (Fig. 1). This was a natural choice; planets never diverge more than about 8° from the ecliptic. However, risings and settings of planets and stars, and their transits of the meridian, are better determined using the equator as the reference circle, with right ascensions α measured along the equator from the vernal equinox $\Upsilon$ and declinations δ measured at right angles to the equator. A standard problem dating as far back as Ptolemy’s Almagest was: given a star’s position with respect to the ecliptic $\left( {\lambda ,\beta } \right)$ and the inclination $\varepsilon \approx 23\frac{1}{2}^\circ$ between the ecliptic and the equator, what are α and δ?

Fig. 1

Ecliptic and equatorial coordinates of a star

Ptolemy provides a solution in Almagest VIII.5, but it leaves a gap in the argument: it requires the value of $\delta_{2}$ in Fig. 1 (called the second declination in medieval Islam) but does not explain how to calculate it.² The gap remained in al-Battānī’s Zīj (ca. AD 900), the earliest source for medieval European astronomers dealing with this question. Those who worked on it replaced $\delta_{2}$ with arc $\delta_{ \odot }$ (dashed in Fig. 1)―the declination of point X, which has no latitude. $\delta_{ \odot }$, considered as a function of $\lambda$, was one of the first quantities tabulated in astronomical handbooks. The difference between the arcs $\delta_{2}$ and $\delta_{ \odot }$ is the location of the right angle: for $\delta_{2}$ it is on the ecliptic; for $\delta_{ \odot }$ it is on the equator. Bianchini corrects the error in the Tabulae primi mobilis with a solution that he says is inspired by Ptolemy, and he provides a set of tables to allow readers to determine α and δ themselves. Incidentally, one of those tables is the first step in a historical process that led eventually to the modern tangent function.

Several intriguing passages in the Tabulae primi mobilis, including the following quotation, suggest that there may have been more to Bianchini’s work on stellar coordinates:

…many users and makers of tables had erred clearly and perceptibly in this matter. And even I was deceived in something similar at another time. And before I had understood the valuable book of the Almagest, when false doctrine was accepted by other quite famous [people], I composed certain tables corresponding to our climate (45°), and they diverged from the truth by a fair amount. No man must be ashamed if his own error is corrected by others; nor am I ashamed to correct my own erroneous proposition. Therefore I have composed tables necessary for this [purpose]. Accordingly, around the end of this little work let me state that these things are performed most truly and according to truths, as I have demonstrated its power above.³

My 2018 paper was our first hint that Bianchini had written an earlier treatise that contained the error. Since then, I have found this original work complete in one manuscript, all but one large table in a second manuscript, the canons in a third, and fragments of the collection of tables in two others. This new text (which we shall call Tabulae primi mobilis A) has not been noticed before now, presumably because it shares most of its introduction with the later work (Tabulae primi mobilis B). The two treatises share about one quarter of their content, both in the canons and in the tables.

Our goal here is to describe the contents of the two books and to analyze the approach to stellar coordinates in the Tabulae primi mobilis A. This new material allows us to question much more precisely Bianchini’s motivation: was the Almagest really his inspiration to abandon the old book and write another? What exactly did he consider a “[divergence] from the truth by a fair amount”? This episode provides a unique opportunity to observe a creative 15th-century astronomer faced with an error in his own work, to consider his criteria for the success or failure of a theory, and to witness his attempt to emerge from mathematical crisis.

2 The manuscripts

The contents of both versions of the Tabulae primi mobilis are quite consistent from one manuscript to the next. This includes the tables―a somewhat unusual feature for the time, since manuscript compilers often gathered together their preferred tables from different sources, leading to malleable boundaries between table collections.

The manuscripts of the newly discovered Tabulae primi mobilis A are:⁴

• A: Florence, Ashburnham 142 (216), 1r-22r (canons); 23r-93r (tables).

• B: Florence, Biblioteca Medicea Laurenziana, Plut.29.33, 122r-134v (canons); 138r-149v (tables, fragment).

• C: Munich, Bayerische Staatsbibliothek, Clm 14111, 102r-116v (tables, fragment).

• D: Nuremberg, Stadtbibliothek, Cent V, 58, 133r-154r (canons).

• E: Würzburg, Universitätsbibliothek, M. ch. f. 254, 111r-126r (tables, fragment).

Only Ashburnham 216 is essentially complete, containing the full 54-page “Tabula universalis ascensionum prima”. The others include only a page or two of this fundamental table.

The manuscripts of the Tabulae primi mobilis B are as follows. Another of Bianchini’s table collections, the Tabulae magistrales (a set of tables that Bianchini composed to ease computational burdens in spherical astronomy and astrology), is very closely associated with the Tabulae primi mobilis B. Their folio numbers are included below, indicated by TM.

• F: Bologna, Biblioteca Comunale dell’Archginnasio, 1601: 1r-17r (canons); 31r-66r, 67r-68r, 69v, 71v-72r, 74v-85r, 98v-99r (tables); 66v, 85v-92v (TM).

• G: Cracow, Biblioteka Jagiellońska, 556: 5r-8r (additions);⁵ 9r-23v (canons); 34v-36v (additions); 40r, 47r-v, 55r-92v, 94r-105v (tables); 48r-54v, 93r (TM).

• H: Innsbruck, Bibliothek des Tiroler Landesmuseums Ferdinandeum, W. 3277: 47r-64v (canons).

• I: Oxford, Bodleian Library, Can. Misc. 517: 82r-99r (canons); 116r-153r, 160r-171r (tables); 172r-177v (TM).⁶

• J: Paris, Bibliothèque Nationale, Latin 7270: 143r-146v (canons, fragment); 147r-167r (canons); 183r, 186v-227v, 231r-236r (tables); 183v-186r, 228r-230v (TM).

• K: Paris, Bibliothèque Nationale, Latin 7271:147r-161r (canons); 181r, 184v, 190r-216v, 222r-237r, 242r-245v (tables); 181v-187v (TM).

• L: Paris, Bibliothèque Nationale, Latin 7286: 65r-81v (canons); 95r-131v, 133r, 136r-136v, 139r-148v (tables); 132v, 149r-154v (TM).

• M: Paris, Bibliothèque Nationale, Latin 10265: 85r, 88v-91r, 92v, 153v-222r, 232v-235r (tables); 223v-232r, 237r-238r (TM).

• N: Paris, Bibliothèque Nationale, Latin 10267: 45r-80v (canons).

• O: Biblioteca Apostolica Vaticana Vat. Lat. 2228: 52r-78r (canons).

The Tabulae magistrales also exist independently in two manuscripts: Cracow, Biblioteka Jagiellońska, 606 (62r-69r) and Vatican, Biblioteca Apostolica Vaticana Vat. Lat. 3538 (6r-7r).

3 Contents of the two works: canons

The first several pages of both versions of the Tabulae primi mobilis deal mostly with astrological matters. They are identical, although the second version uses a different numerical example. The last couple of sentences of the introduction to the Tabulae primi mobilis A advertise the presence of tables that apply to any terrestrial location, but there is no reference to Bianchini’s foundational work of mathematical astronomy, the Flores Almagesti, or to his Tabulae magistrales, anywhere in the treatise. On the other hand, the introduction to the Tabulae primi mobilis B describes the Flores Almagesti chapter by chapter and refers to it frequently in the rest of the canons; it also concludes with a reference to the Tabulae magistrales. This suggests that much of the Flores Almagesti and the Tabulae magistrales were composed between the two versions of the Tabulae primi mobilis.

The appendix to this article contains tables of contents of the canons of the two versions of the Tabulae primi mobilis, indicating in bold face chapters where the texts are essentially the same.⁷ Bianchini re-appropriated about one quarter of the content of the original text for the revised work, preserving hardly any of the trigonometry, parts of the spherical astronomy, and most of the astrology.

4 Contents of the two works: tables

In Alfonsine astronomy, numerical tables are sometimes found in the manuscripts as coherent collections, but often individual tables had lives of their own. If a manuscript compiler found a particular table to be useful to him, he would not hesitate to copy it detached from the collection it came from, and often even from the instructions for the table’s use. Thus it can be difficult to define clearly which tables are part of a given work and which are not. In this case, however, the table collections of the two versions of the Tabulae primi mobilis have fairly clearly defined boundaries. This may be due partly to the unique system of arithmetic invented by Bianchini, and partly to his theoretical innovations.

In the tables of contents below, we exclude tables that are found in two or fewer of the ten manuscripts that include tables.⁸ Only four tables are common to both versions of the Tabulae primi mobilis. Two are trigonometric, and two are related to an astrological innovation (on which we shall publish a paper shortly):⁹

• Tabula sinus (A: 23r-24v, B: 138r-139r, C: 102r-103v, E: 111r-112v, F: 31r-32v, G: 57r-58v, J: 231r-232v, K: 235r-236v, L: 95r-96v, M: 232v-235r).

• Tabula umbre (A: 29r-30r, B: 142r-142v, C: 107v-108v, E: 116v-117v, G: 47r-47v, L: 97r-98r).

• Tabula horarum diei prolixioris in omni regione (A: 28v, B: 143r, C: 109r, E: 126r, F: 68r, G: 105v, J: 186v, K: 184v, 242r, L: 133r).

• Tabula de aspectibus et proiectionibus radiorum (A: 93r, B: 148r, C: 109r, E: 126r, F: 68r, G: 105r, K: 242r, L: 133r, M: 85r).

Ten tables are found only in the Tabulae primi mobilis A:¹⁰

• Tabula declinationis secundum almeon qui dictus est Arzachel (A: 25r-26r, B: 139v-140r, C: 104r-105r, E: 113r-114r).

• Tabula sinus declinationis (A: 26v-28r, B: 140v-141v, C: 105v-107r, E: 114v-116r).

• Tabula ad inveniendum gradus cum quibus quelibet stella oritur in omni regione (A: 89v, B: 143r, C: 115v, E: 125v).

• Tabula ad inveniendum cum quo gradus quelibet stella mediat celum in omni regione (A: 89v, B: 143r, C: 115v, E: 125v).

• Tabula prima verarum declinationum ad latitudines stellarum in parte declinationis (A: 31v-32r, 90r-91v, B: 144r-146r, C: 111v-115r).

• Tabula secunda verarum declinationum ad latitudines stellarum in parte contraria declinationis (A: 32v-33r, 91v-93r, B: 146r-148r).

• Tabula longitudinis et latitudinis civitatum (A: 28v (blank), B: 148r).

• Tabula universalis ascensionum prima (A: 60v-87r, B: 148v, C: 109v-110r, E: 118v-119r).¹¹

• Tabula universalis ascensionum secunda (A: 87v-88r, B: 149r, E: 119v-120r).

• Tabula universalis ascensionum tertia (A: 88v-89r, B: 149v, C: 110v-111r, E: 120v-121r).

The 54-page table Tabula de ascensionibus stellarum habentium latitudinem ab ecliptica in regione sexto climate latitudinis gradus 45 tabulates stellar right and oblique ascensions. It is fundamental to the work as a whole, but only the scribe of A seems to have had the fortitude to copy it in its entirety. Although it has the same title as a table in the Tabulae primi mobilis B, its entries are different. We shall examine this table below.

Ten tables are found only in the Tabulae primi mobilis B:

• Tabula novissima declinationis ecliptice per arcum (F: 33r, G: 59r, J: 236r, K: 242v, L: 98v, M: 92v).

• Tabula radicum ascensionum (F: 33v, G: 59v, J: 183r, K: 181r, L: 99r, M: 221v).

• Tabula declinationis stellarum cum sua latitudine in parte declinationis arcum vere declinationis (F: 34r-39r, G: 60r-65r, J: 187r-187v, K: 244r-245r, L: 99v-104v, M: 88v-90r).

• Tabula de ascensionibus stellarum habentium latitudinem ab ecliptica in sexto climate latitudinis gradus 45 (F: 39v-66r, G: 66r-92v, J: 191v-218r, K: 190r-216v, L: 105r-131v, M: 153v-180r).

• Tabula de ascensiones signorum in circulo directo (F: 72r, 74v, G: 95r, J: 221r, K: 223r, L: 139r-139v, M: 180v-181r).

• Tabula de ascensiones signorum in circulo obliquo (F: 75r-85r, 98v-99r, G: 96r-104v, J: 221v-227v, K: 224r-234r, L: 140r-148v, M: 181v-204r, 210v-221r).

• Tabula correspondens ascensionibus medii coeli ad inveniendum gradus ascendentem in regione latitudinis g. 45… (J: 188r, K: 245v, M: 90v-91r).

• Tabula horarum meridiei in climati sexto cum equationibus dierum cum noctibus suis (F: 69v, J: 220v, K: 222r (empty), L: 136v, M: 205v-206r).

• Tabula angulorum meridionalum et orbe signorum in omni regione (F: 71v, G: 40r, J: 233r, K: 237r, L: 136r, M: 222r).

• Tabula vere declinationis ecliptice (F: 71v, J: 233r, K: 237r, L: 136r, M: 92v).

5 Bianchini’s original solution to the stellar coordinates problem

We have already described Bianchini’s corrected solution to the stellar coordinates problem in Van Brummelen (2018). Here, we describe his original solution as outlined in the canons and tables of the Tabulae primi mobilis A, and compare it with the corrected solution.

Recall that the problem is as follows: given a star’s ecliptic coordinates $\left( {\lambda ,\beta } \right)$ and the obliquity of the ecliptic $\varepsilon$ (Bianchini’s value is 23;33,30°), determine the star’s equatorial coordinates $\left( {\alpha ,\delta } \right)$. Bianchini begins, as did his predecessors, with the determination of the star’s declination $\delta$ (Chapter 7, part 7 of his canons). In Fig. 1, the star’s latitude $\beta$ is measured perpendicularly from point X on the ecliptic. Arc $\widehat{XZ}$ is taken to be the solar declination $\delta_{ \odot }$ of X, calculated using the standard formula

$$ \sin \delta_{ \odot } = \sin \lambda \sin \varepsilon . $$

Bianchini provides a table for $\delta_{ \odot }$ that he says was computed by “Almeon, qui dictus est Arzachel”, a mistaken identification of the 9th-century Baghdad caliph al-Ma’mun with the 11th-century Toledan astronomer al-Zarqālī.¹²

Next, Bianchini applies the “conjunction” version of Menelaus’s Theorem to the configuration indicated with gray arcs in Fig. 1,¹³ giving

$$ \sin \delta = \frac{{\sin \left( {\delta_{ \odot } + \beta } \right) \cdot \cos \varepsilon }}{{\cos \delta_{ \odot } }}. $$

He instructs the reader to use his Tabula sinus declinationis, which tabulates $\sin \delta_{ \odot } \left( \lambda \right)$ and $\cos \delta_{ \odot } \left( \lambda \right)$, to find $\cos \delta_{ \odot } \left( \lambda \right)$ and $\cos \varepsilon = \cos \delta_{ \odot } \left( {90^\circ } \right)$.¹⁴ This is similar to Ptolemy’s method in Almagest VIII.5, but with an error: $\beta$ and $\delta_{ \odot }$ are not part of the same great circle. This is the error to which Bianchini would later refer frequently in the Tabulae primi mobilis B.¹⁵ The continuation of $\widehat{*X}$ to the equator at Z is the solar second declination $\delta_{2}$, which had been named as such in eastern Islam in the 10th century and tabulated frequently ever since. Several of Bianchini’s predecessors, including Richard of Wallingford, John of Lignères, and John of Gmunden, had committed the same error during the previous century.¹⁶

Bianchini provides two tables to free the reader from having to perform this calculation: Tabula prima verarum declinationum ad latitudines stellarum in parte declinationis and Tabula secunda verarum declinationum ad latitudines stellarum in parte contraria declinationis. Both give $\delta \left( {\lambda ,\beta } \right)$ for $\lambda = 0^\circ , 1^\circ , 2^\circ , \ldots 90^\circ$ and for $\beta = 1^\circ , 2^\circ , \ldots 8^\circ$―the range of latitudes that covers all possible positions of the planets. In Chapter 15, Bianchini explains that the first table is to be used when $\delta_{ \odot }$ and $\beta$ are both northward or both southward (so that their values are added within the sine term of the numerator in the formula above); the second table is to be used when $\delta_{ \odot }$ and $\beta$ are in opposite directions (so that they are subtracted). Most entries are accurate to within 1′ of arc. The differences between the values of the stellar declination in these original tables and the correct values found in the Tabulae primi mobilis B range between 0 and 49′ of arc.

Chapter 7 part 8 describes the computation of $\alpha \left( {\lambda ,\beta } \right)$; Bianchini employs the incorrect formula

$$ \sin d = \frac{{\sin \beta \sin \varepsilon \cos \alpha_{ \odot } }}{{\cos \delta_{ \odot } }}, $$

where d is the difference between $\alpha$ and the solar right ascension $\alpha_{ \odot }$ (see Fig. 1). The determination of $\alpha_{ \odot }$ was well known, for instance by Ptolemy’s equivalent to $\sin \alpha_{ \odot } = \tan \delta_{ \odot } \cot \varepsilon$, so having d allows Bianchini to find $\alpha$. He says that his method was demonstrated in Almagest VIII.5, but this is not true; this attribution was already denied in a marginal note in one of the manuscripts.¹⁷ The formula in al-Battānī’s zīj is

$$ \sin d = \frac{\sin \beta \sin \varepsilon \cos \lambda }{{\cos \delta_{ \odot } \cos \delta }}, $$

which is correct (assuming that $\delta$ had been found correctly in the first place).¹⁸ One may apply the spherical Pythagorean theorem $\cos \alpha_{ \odot } = \cos \lambda /\cos \delta_{ \odot }$ to get Bianchini’s formula from this, but there is still a mistake, since he has $\cos \delta_{ \odot }$ in his denominator rather than $\cos \delta$. However, Bianchini’s error has the (presumably accidental) benefit of removing the errant value of $\delta$ from his calculation. Indeed, the differences between stellar right ascensions calculated according to Bianchini’s method and according to the correct method rise gradually as $\left| \beta \right|$ increases, but never reach 10′ of arc in the range of arguments of his table.

Bianchini’s table for $\alpha \left( {\lambda ,\beta } \right)$ is one of two quantities tabulated in Tabula de ascensionibus stellarum habentium latitudinem ab ecliptica in regione sexto climate latitudinis gradus 45. The vast majority of the 6120 entries in this table match Bianchini’s formula to within 1′ of arc.¹⁹

In Chapter 7 part 9 Bianchini tackles the problem of calculating oblique ascensions $\theta$, but only for his terrestrial latitude, which happens to be $\varphi = 45^\circ$. The oblique ascension $\theta \left( {\lambda ,\beta ,\varphi } \right)$ is found by subtracting the ascensional difference $\gamma$ from the right ascension $\alpha$ (see Fig. 2). The general formula for $\gamma$ is $\sin \gamma = \tan \delta \tan \varphi$, so Bianchini was fortunate living where he did, since at $\varphi = 45^\circ$ it simplifies to $\sin \gamma = \tan \delta$. Computing a couple of other quantities along the way, he eventually arrives at $\theta$. He tabulates $\theta \left( {\lambda ,\beta ,45^\circ } \right)$ as the ascensionis orientis, the second quantity given in Tabula de ascensionibus stellarum habentium latitudinem ab ecliptica in regione sexto climate latitudinis gradus 45. Again, almost all of the 6120 entries match Bianchini’s formula either precisely or to within a few minutes of arc. However, the entries for $\beta = 0^\circ$ differ substantially from this formula (usually by tens of minutes of arc), and agree with the oblique ascension table in the Tabula primi mobilis B. Thus either Bianchini computed entries for this simpler case using some version of the correct formula, or the corrected values were copied into the table in this manuscript.

Fig. 2

Finding a star’s oblique ascension

But what about readers who do not live at $\varphi = 45^\circ$ ? For them, Bianchini designs a set of three “universal” tables to find oblique ascensions; he describes their theory in Chapter 11, and their use in Chapter 12. The first table contains two quantities. The first is $\theta_{1,1} = \alpha \left( {\lambda ,\beta } \right)$, copied from his stellar right ascension table. The second, called the numerus multiplicandus, turns out to be the sine of the ascensional difference $\gamma$ when $\varphi = 45^\circ$. Since in this case we have $\sin \gamma = \tan \delta$, the tabulated quantity is just $\theta_{1,2} = \tan \delta$.²⁰ The 2520 entries in this table are almost all accurate to within 1 or 2 units in the last decimal place (except, again, for those with $\beta = 0^\circ$).

The second universal table of ascensions simply gives $\theta_{2} \left( \varphi \right) = \tan \varphi$ (for increments of 10′ of arc), which Bianchini notes is the reciprocal (conversa) of a shadow table. The third universal table of ascensions is $\theta_{3} \left( x \right) = \sin^{ - 1} x$. This is the earliest European arc sine table of which I am aware,²¹ although since Bianchini uses it only in this single context, it cannot properly be called a trigonometric table. To find $\theta \left( {\lambda ,\beta ,\varphi } \right)$, the reader is instructed to evaluate

$$ \theta_{1,1} \left( {\lambda ,\beta } \right) - \theta_{3} \left( {\theta_{1,2} \left( {\lambda ,\beta } \right) \cdot \theta_{2} \left( \varphi \right)} \right). $$

This corresponds to

$$ \alpha \left( {\lambda ,\beta } \right) - \sin^{ - 1} \left( {\tan \delta \cdot \tan \varphi } \right), $$

which is indeed the oblique ascension, since it is the right ascension $\alpha$ minus the ascensional difference $\gamma$. Of course, the use of the errant stellar declination $\delta$ introduces an error into these calculations.

6 Discussion

In the improved Tabulae primi mobilis B, Bianchini credits the Almagest as his inspiration to replace his original work. We are now in a position to evaluate the extent to which this is true. Although Bianchini praises Ptolemy effusively in the introduction to the Tabulae primi mobilis A, he does not rely on it in any substantial way to deal with stellar coordinate conversion, the astronomical heart of the book. His calculations for the stellar declination $\delta \left( {\lambda ,\beta } \right)$ indeed may be inspired by Almagest VIII.5. However, the facts that he falls into the same error that his immediate predecessors had done, and that his flawed version of a formula for the stellar right ascension $\alpha \left( {\lambda ,\beta } \right)$ is present in al-Battānī’s zīj, imply that an immediate connection with Ptolemy need not be assumed.

The Tabulae primi mobilis B, while imperfect in some sections, is a more mature and mathematically sound work. Its solution to the stellar coordinate conversion problem is both correct and elegant. A simple comparison of his original stellar declination table with his newer one immediately would have allowed Bianchini to see that the magnitude of the original error was often on the order of tens of minutes of arc, occasionally as high as 3/4 of a degree. This is likely what he meant when he said that the original tables “diverged from the truth by a fair amount” (aliquantum a veritate discrepabant). As we have seen, the stellar right ascension tables are more accurate, ironically partly because another error removed the incorrect stellar declination values from the calculation.

Bianchini’s mathematical method itself is not entirely due to Ptolemy. However, its adherence to formal mathematical argument and reliance on Menelaus’s Theorem may well have been modeled on the Almagest. Bianchini’s debt to Ptolemy may rest not so much with particular problems and solutions, but rather with his consistent use of mathematical derivations to establish his results. The vast majority of the spherical astronomy in his Flores Almagesti, on which I shall present a paper in the near future, is written in this genre. It seems, then, that the greatest inspiration that Bianchini found in the Almagest may well have been not so much in what he wrote, but rather in the way that he wrote.

Appendix: tables of contents of the two sets of canons

In the tables of contents below, each chapter that is essentially identical to a chapter in the other version of the Tabulae primi mobilis is indicated with a remark in bold face. Following the introduction, the Tabulae primi mobilis A begins with Chapter 2; the Tabulae primi mobilis B begins with Chapter 1.

1.1 Tabulae primi mobilis A

• 2. Secuntur considerationes et diffinitiones ceterorum terminorum cum demonstrationibus quarundam figurarum pro compositione tabularum cum certis regulis necessarias (includes a diagram).²²

• 3. De diffinitione trianguli ortogonii (includes a diagram).

• 4. Demonstratio plurium triangulorum ortogonorum super solam ypothenusam constitutorum (includes two diagrams).

• 5. De compositione tabule umbre (includes a diagram).

• 6. De numeris ignotis per ipsorum proportiones eorum notitiam pervenire.

• 7. De tabulis per Johannem Blanchinis compositis et de doctrina ipsarum componendarum super primo mobili.

• 8. Altitudinem meridianam cuiuscumque stelle in quacumque regione volueris invenire. (Chapter 22 in Tabulae primi mobilis B)

• 9. Horas diei per solis altitudinem invenire.

• 10. Horas noctis per stellas tibi notas indagare.

• 11. De compositione novissima trium tabularum per Johannem Blanchinis noviter factarum ad componendum tabulas de ascensionibus stellarum tam latitudinem habentium quam in ecliptica existentium generaliter in omni regione ac de operatione et utilitate ipsarum.

• 12. De operatione trium tabularum.

• 13. Sinum primum et secundum portionis arcus date per tabulas Johannis de Blanchinis invenire.

• 14. Declinationem veram cuiuscumque gradus ecliptice ab equinoctiali perscrutari.

• 15. Declinationem veram stellarum habentium latitudinem per tabulas Johannis de Blanchinis invenire.

• 16. Sinum versum per easdem tabulas indagare.

• 17. Sinum primum et secundum declinationis gradus ecliptice cuiuscumque ab equinoctiali invenire.

• 18. Umbram cuiuscumque gradus altitudinis per tabulas indagare. ²³

• 19. Per sinum rectum aut declinationem seu umbram datam gradus circuli indagare.

• 20. Per sinum secundum datum gradum circuli indagare.

• 21. Per sinum versum gradus circuli perscrutari.

• 22. Latitudinem cuiuscumque regionis per solis altitudinem invenire.

• 23. Latitudinem regionis cuiuscumque per stellas fixas indagare. (Chapter 24 in Tabulae primi mobilis B²⁴)

• 24. Latitudinem regionis per notitiam diei prolixioris in anno per tabulas Johannis de Blanchinis invenire, et converso. (Chapter 36 in Tabulae primi mobilis B)

• 25. De concordantia ascensionum stellarum tam in ecliptica existentium quam cum latitudine ab ipsa in utraque parte et tam in spera recta quam obliqua. (Chapter 28 in Tabulae primi mobilis B)

• 26. Gradus ascensionum cum quibus stella quelibet tam habens latitudinem quam non, oritur mediat celum et occidit per tabulas Johannis de Blanchinis invenire. ²⁵

• 27. Ad inveniendum gradum ascensionum cum quibus stella transit per circulos horarum tam supra orizontem quam sub orizonte. ²⁶

• 28. Partes horarum gradus ascensionis stelle et per consequens arcum diurnum et nocturnum ipsius invenire.²⁷ (Chapter 32 in Tabulae primi mobilis B)

• 29. Figuram celestem 12 domorum per tabulas Johannis de Blanchinis erigere ad situm huius 6 climatis latitudinis gradus 45.

• 30. Stellas fixas seu planetas habentes latitudinem ab ecliptica in figura celesti per tabulas Johannis de Blachinis collocare. (Chapter 33 in Tabulae primi mobilis B)

• 31. Distantiam significatoris seu cuiuscumque alie stelle in figure celesti collocate ad quemcumque angulum figure perscrutaris. ²⁸

• 32. De opinionibus quorundam in directionibus. (Chapter 35 in Tabulae primi mobilis B²⁹)

• 33. De directionibus qui fiunt per gradus equales.³⁰ (Chapter 42 in Tabulae primi mobilis B)

• 34. De directionibus que fiunt per ascensiones circuli directi. (Chapter 43 in Tabulae primi mobilis B)

• 35. De directionibus que fiunt per ascensiones regionis. ³¹

• 36. De regulis Ptholomei et aliorum ipsum sequentium in directionibus. (Chapter 45 in Tabulae primi mobilis B)

• 37. De modo dirigendi significatorem in cuspide medii celi seu anguli terre existentem.³² (Chapter 46 in Tabulae primi mobilis B)

• 38. De modo dirigendi significatorem existentem in linea ascendentis. (Chapter 47 in Tabulae primi mobilis B)

• 39. De modo dirigendi significatorem existentem in linea occidentis.

• 40. De directionibus inveniendis quando significator extra cuspides angulorum et primo quando significator fuerit inter cuspidem domus 10 ^e et ascendentis. ³³

• 41. De modo dirigendi significatorem existentem inter medium celi et occidentem. ³⁴

• 42. De eodem significatore inter angulum terre et occidentem.

• 43. De significatore existente inter angulum ascendentis et angulum 4 ^e domus. ³⁵

• 44. De aspectibus et proiectionibus radiorum machinatio pulcherrima. (Chapter 37 in Tabulae primi mobilis B³⁶)

• 45. De modo operandi per tabulam de aspectibus et proiectionibus radiorum compositam per Johannem Blanchinum.

• 46. Exemplum de modo collocandi planetas et alias stellas in figura proiciendique radios aspectuales cum directionibus ipsorum.

• 47. Si aliquid boni seu mali in aliquo anno post navitatem nati evenire debeat perscrutari.

• 48. Argumentum contra proicentes radios planetarum per circulum equinoctialem. (Chapter 41 in Tabulae primi mobilis B³⁷)³⁸

1.2 Tabulae primi mobilis B

• 1. De sinu et arcu.

• 2. De multiplicatione sinuum aduinicem.

• 3. De divisione sinuum.

• 4. De ordine compositionis tabularum sinuum.

• 5. Sinum primum vel secundum cuiuslibet arcus invenire.

• 6. Sinum versum per arcum datum invenire.

• 7. Per sinum primum seu sinum rectum gradus circuli indagare.

• 8. Per sinum secundum datum gradus circuli invenire.

• 9. Per sinum versum quantitatem arcus sibi correspondentis invenire.

• 10. Declinationem veram eclyptice ab equinoctiali invenire.

• 11. De parte proportionali extrahenda.

• 12. De radice ascensionum stellarum que est de ascensionibus stellarum in eclyptica existenti per arcus latitudinis terminatum secundum Ioannem blanchinum invenienda.

• 13. Ascensiones signorum in eclyptica existentium in medio celi que est tabula communis invenire.

• 14. Declinationem eclyptice ab equinoctiali per arcus latitudinis invenire.

• 15. Declinationem veram stelle habentis latitudinem perscrutari.

• 16. Ascensiones veras stelle hanebntis latitudinem in medio celi inquirere.

• 17. Gradum eclyptice correspondentem stelle habenti latitudinem in medio celi inquirere.

• 18. Ascensiones cuiuscumque gradus eclyptice atque arcum diurnum ipsius in quacunque regione volueris invenire.

• 19. Partes horarum cuiuslibet stelle invenire.

• 20. Arcum diurnum cuiuscumque stelle habentis latitudinem in quacunque regione volueris invenire.

• 21. Ascensiones cuiuscumque stelle habentis latitudinem in regione quacunque invenire.

• 22. Altitudinem meridianam solis et cuiuscumque altitudinis stelle in quacunque regione volueris invenire. (Chapter 8 in Tabulae primi mobilis A)

• 23. Latitudinem cuiuscumque regionis per solis altitudinem invenire.

• 24. Latitudinem regionis per stellas fixas indagare. (Chapter 23 in Tabulae primi mobilis A)

• 25. Horas diei transactas per solis altitudinem invenire.

• 26. Horas in nocte transactas per altitudinem cuiuscumque stelle orientis et occidentis tibi note invenire.

• 27. De tabulis compositis.

• 28. De concordia ascensionum stellarum tam in eclyptica existentium quam in latitudine ab ipsa declinata et tam in spera recta quam etiam in obliqua. (Chapter 25 in Tabulae primi mobilis A)

• 29. Figura celestem 12 domorum in quacunque regione erigere.

• 30. Gradus ascensionum cum quibus stella quelibet habens latitudinem oritur mediat celum et occidit in regione nostra latitudinis gradus 45 et gradus eclyptice ipsis correspondentes per tabulas invenire.

• 31. Gradus ascensionum cum quibus stella quelibet transit per circulos horarum perscrutari.

• 32. Partes horarum stellarum suprascriptarum habentium latitudinem et per consequens arcum diurnum ipsarum invenire. (Chapter 28 in Tabulae primi mobilis A)

• 33. Stellas fixas seu planetas habentes latitudinem ab eclyptica in figura celesti collocare. (Chapter 30 in Tabulae primi mobilis A)

• 34. Distantiam significatoris seu cuiuscumque alterius stelle in figura celesti collocare ad quemcunque angulum figure perscrutari.

• 35. De opinionibus quorundam in directionibus. (Chapter 32 in Tabulae primi mobilis A)

• 36. Latitudinem regionum per notitiam diei proxioris in anno et econverso diem prolixiorem per latitudinem invenire. (Chapter 24 in Tabulae primi mobilis A)

• 37. De aspectibus et proiectionibus radiorum machinatio pulcherrima. (Chapter 44 in Tabulae primi mobilis A)

• 38. De latitudine cuiuslibet aspectus planetarum ab eclyptica absque tabulis invenire.

• 39. Arcum eclyptice correspondentem cuilibet aspectui tabularum absque tabulis perscrutari.

• 40. Vera loca cuiuscumque aspectus planetarum per longitudinem et latitudinem per tabulas terminare.

• 41. Argumentum contra proiectiones radiorum planetarum per circulum equinoctialem. (Chapter 48 in Tabulae primi mobilis A)

• 42. De directionibus que fiunt per gradus equales. (Chapter 33 in Tabulae primi mobilis A)

• 43. De directionibus que fiunt per ascensiones circuli directi. (Chapter 34 in Tabulae primi mobilis A)

• 44. De directionibus que fiunt per ascensiones regionis.

• 45. De regulis Ptholomei et aliorum ipsum sequentium de directionibus per ascensiones mixtas. (Chapter 36 in Tabulae primi mobilis A)

• 46. De modo dirigendi significatorem in cuspide medii celi seu anguli terre existentis. (Chapter 37 in Tabulae primi mobilis A)

• 47. De modo dirigendi significatorem existentem in linea ascendentis. (Chapter 38 in Tabulae primi mobilis A)

• 48. De significatore existente in linea occidentis.

• 49. De directionibus inveniendis quando significator fuerit extra cuspides domorum seu angulorum et primo quando fuerit inter cuspidem 10 ^e domus et ascendentem.

• 50. De directionibus inveniendis quando significator fuerit inter domum 10 ^am et occidentem.

• 51. De eodem significatore existente inter angulum terre et occidentem.

• 52. De significatore existente inter ascendentem et angulum terre.