Skip to main content
SpringerLink
Log in

Waves on viscoelastic films

  • Original contribution
  • Published:
Rheologica Acta Aims and scope Submit manuscript

Abstract

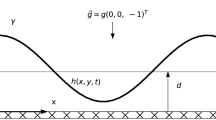
The stability of films of a viscoelastic fluid on an inclined plane is considered. The stress contains a time-dependent memory term and takes into account the surface tension effect. It is shown analytically and numerically that these flows can be stable or unstable depending on the Reynolds number. Profiles of the free surface are obtained as functions of the Reynolds numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Astarita G, Marucci G (1974) Principles of non-Newtonian fluid mechanics. McGraw Hill

  • Benney DJ (1966) Long waves on liquid films. J Math Phys 45:150–155

    Google Scholar 

  • Berezin YA, Hutter K, Spodareva LA (1998a) Stability analysis of gravity driven shear flows with free surface for power-law fluids. Arch Appl Mech 68:169–178

    Article  Google Scholar 

  • Berezin YA, Hutter K, Spodareva LA (1998b) Stability properties of shallow granular flows. Int J Non-Linear Mech 33:647–658

    Google Scholar 

  • Berezin YA, Hutter K, Spodareva LA (2000) Evolution of disturbances on shallow non-Newtonian fluids. Physica D 139:319–334

    Article  Google Scholar 

  • Berezin YA, Chugunov VA, Hutter K (2001) Hydraulic jumps on shallow layers of non-Newtonian fluids. J Non-Newtonian Fluid Mech 101:139–148

    Google Scholar 

  • Chang HC (1994) Wave evolution on a falling film. Annu Rev Fluid Mech 26:103–136

    Article  Google Scholar 

  • Chang HC, Demekhin EA, Kopelevich DI (1993) Nonlinear evolution of waves on a falling film. J Fluid Mech 250:433–480

    CAS  Google Scholar 

  • Coleman BD, Noll W (1960) An approximation theorem for functionals, with applications in continuum mechanics. Arch Rational Mech Anal 6:355–370

    Google Scholar 

  • Dandapat BS, Gupta AS (1978) Long waves on a layer of a visco-elastic fluid down an inclined plane. Rheol Acta 17:492–499

    Google Scholar 

  • Dandapat BS, Gupta AS (1997) Solitary waves on the surface of a visco-elastic fluid running down an inclined plane. Rheol Acta 36:135–145

    Article  CAS  Google Scholar 

  • Gupta AS (1967) Stability of a visco-elastic liquid film flowing down an inclined plane. J Fluid Mech 28:17–28

    Google Scholar 

  • Gupta AS, Rai L (1968) Note on stability of a visco-elastic liquid film flowing down an inclined plane. J Fluid Mech 33:87–91

    Google Scholar 

  • Hwang C, Chen J, Wang J, Lin J (1994) Linear stability of power-law liquid film flowing down an inclined plane. J Phys D Appl Phys 27:2297–2301

    Article  CAS  Google Scholar 

  • Lee JJ, Mei CC (1996) Stationary waves on an inclined sheet of viscous fluid at high Reynolds and moderate Weber numbers. J Fluid Mech 307:191–229

    CAS  Google Scholar 

  • Lin SP (1974) Finite amplitude side-band stability of a viscous film. J Fluid Mech 63:417–429

    Google Scholar 

  • Mei CC (1966) Nonlinear gravity waves in a thin sheet of viscous fluid. J Math Phys 45:266–288

    Google Scholar 

  • Ng C, Mei CC (1994) Roll waves on a shallow layer of mud modelled as a power-law fluid. J Fluid Mech 263:151–183

    Google Scholar 

  • Pumir A, Manneville P, Pomeau Y (1983) On solitary waves running down an inclined plane. J Fluid Mech 135:27–50

    Google Scholar 

  • Trifonov YY, Tsvelodub OY (1991) Nonlinear waves on the surface of a falling liquid film. J Fluid Mech 229:531–554

    CAS  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge financial support by the Deutsche Forschungsgemeinschaft via its SFB 298 “Deformation and Failure of Metallic and Granular Structures”.

Author information

Authors and Affiliations

  1. Institute of Theoretical and Applied Mechanics, 630090, Novosibirsk, Russia

    Y. A. Berezin

  2. Institut für Mechanik, Technische Universität, Darmstadt, 64289, Darmstadt, Germany

    K. Hutter

Authors
  1. Y. A. Berezin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Hutter
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. Hutter.

Additional information

Y. A. Berezin deceased 11.04.2004

Rights and permissions

Reprints and permissions

About this article

Cite this article

Berezin, Y.A., Hutter, K. Waves on viscoelastic films. Rheol Acta 44, 112–118 (2004). https://doi.org/10.1007/s00397-004-0397-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00397-004-0397-0

Keywords

Search

Navigation