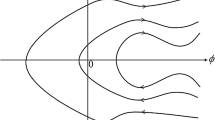
Abstract
The paper analyses a possible occurrence of soft and semi-soft viscous modes in slow (low Reynolds number) flows of uniaxially anisotropic nematic liquids as described by the five parametric Leslie-Ericksen-Parodi (LEP) constitutive equations (CEs). As in the similar elastic case, the soft viscous modes theoretically cause no resistance to flow, nullifying the corresponding components of the viscous part of the total stress tensor, and do not contribute to the dissipation. That is why these modes can also be called dissipative soft modes. In some flows, these dissipative soft modes may cause the effect of “nematic superfluidity”. As in the theories of nematic elastic solids, this effect is caused by a marginal thermodynamic stability. The analysis is simplified in a specific local, rotating orthogonal coordinate system whose one axis is directed along the director. We demonstrate that depending on closeness of material parameters to the marginal stability conditions, LEP CEs describe the entire variety of soft, semi-soft and harder behaviors of nematic viscous liquids. When the only shearing dissipative modes are soft, the viscous part of stress tensor is symmetric, and LEP CE for stress, scaled with isotropic viscosity is reduced to a one-parametric, stress-strain rate anisotropic relation. When additionally the elongation dissipative mode is also soft, this scaled relation has no additional parameters and shows that the dissipation is always less than that in isotropic phase. Simple shearing and simple elongation flows illustrate these possible effects.
Similar content being viewed by others
References
Allen SJ, de Silva CN (1966) A theory of transversely isotropic fluids. J Fluid Mech 24:801–821
Born M (1920) Über die beveglichkeit der electrolytishen ionen. Z Phys 1:221–249
Calderer MC (1991) On multiphase flows of liquid crystal polymers. J Rheol 35:29–47
Clark MG, Saunders FC, Shanks IA, Leslie FM (1981) A study of flow-alignment instability during rectilinear oscillatory shear of nematics. Mol Cryst Liq Cryst 70:1473–1500
de Gennes PG (1980) In: Helfrich W, Kleppke G (eds) Liquid Crystals in one- and two dimensional order. Springer, Berlin Heidelberg New York, pp 231–237
de Gennes PG, Prost G (1993) The physics of liquid crystals, 2nd edn. Clarendon Press, Oxford, chap 5
de Groot SR, Mazur P (1962) Non-equilibrium thermodynamics. North-Holland, Amsterdam, chap 12
Ericksen JL (1960a) Anisotropic fluids. Arch Ration Mech Anal 4:231–237
Ericksen JL (1960b) Transversely isotropic fluids. Kolloid-Z 173(2):117–122
Ericksen JL (1991) Liquid crystals with variable degree of orientation. Arch Rational Mech Anal 113:97–120
Fradkin LJ, Kamotski IV, Terentjev EM, Zakharov DD (1993) Low-frequency acoustic waves in nematic elastomers. Proc R Soc Lond A 459:2627–2642
Geffery GB (1922) The motion of ellipsoidal particles immersed in a viscous fluid. Proc R Soc Lond 102:161–179
Golubovich L, Lubensky TC (1989) Nonlinear elasticity of amorphous solids. Phys Rev Lett 63:1082–1085
Grad H (1952) Statistical mechanics, thermodynamics, and fluid dynamics of systems with an arbitrary number of integrals. Comm Pure Appl Math 5:455–494
Hinch EJ, Leal LG (1973) Time-dependent shear flows of s suspension of particles with weak Brownian rotations. J Fluid Mech 57:753–767
Kamensky VG (1984) Nonlinear director dynamics of nematics in a magnetic field (in Russian). JETP 87:1262–1276
Kleman M (1983) Points, lines and walls. Wiley
Larson RG (1999) The structure and rheology of complex fluids. Oxford University Press, New York
Larson RG, Mead DW (1989) Linear viscoelasticity of nematic liquid crystalline polymers. J Rheol 33:185–206
Leonov AI (1988) Extremum principles and exact two-side bounds of potential functional and dissipation for slow motions of viscoplastic media. J Non-Newtonian Fluid Mech 28:1–28
Leonov AI, Volkov VS (2002) Internal rotations and stress tensor symmetry in theories of nematic liquids and solids. Los Alamos e-print archive: cond.mat/0203265
Leonov AI, Volkov VS (2003) Analysis of weak elasticity of nematic solids using a continuum approach. Los Alamos e-print arxive: cond.mat/0307146
Leonov AI, Volkov VS (2004) General analysis of linear nematic elasticity. J Eng Phys Thermophys 77:N.2
Leslie FM (1968) Some constitutive equations for liquid crystals. Arch Ration Mech Anal 28:265–283
Long D, Morse DC (2002) A Rouse-like model of liquid crystalline polymer melts: director dynamics and linear viscoelasticity. J Rheol 49–92
Lubensky TC, Mukhopadya R (2002) Symmetries and elasticity of nematic gels. Phys Rev E 66:011702
Parodi OJ (1970) Stress tensor for a nematic liquid crystal. J Phys (Fr) 31:581–584
Rubin PL (1981) Relaxation processes and the propagation of ultrasound in nematic liquid crystals (in Russian). JETP 81:1756–1762
Semenov AN (1993) Domain formation in liquid crystals under oscillating shear flows. J Rheol 37:911–917
Sorokin VS (1943) On internal friction of liquids and gases which have a hidden moment of impulse (in Russian) JETP 13:306–312
Stephen MJ, Straley JP (1974) Rev Mod Phys 46:617–704
Terentjev EM, Warner M (2001) Linear hydrodynamics and viscoelasticity of nematic elastomers. Eur Phys J E 4:343–353
Truesdell C, Noll W (1992) The non-linear field theories of mechanics, 2nd edn. Springer, Berlin Heidelberg New York
Ugaz VM, Burghard WR (1998) In situ X-ray scattering study of model thermotropic copolyester under shear: evidence and consequences of flow-aligning behavior. Macromolecules 31:8474–8484
Warner M, Terentjev EM (2004) Liquid crystal elastomers. Clarendon Press, Oxford
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Leonov, A.I., Volkov, V.S. Dissipative soft modes in viscous nematodynamics. Rheol Acta 44, 331–341 (2005). https://doi.org/10.1007/s00397-004-0386-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-004-0386-3