Introduction

Microfluidic systems are often used together with bulky, external pumps; these significantly increase the costs of the system and, moreover, compromise—to a large extent—their autonomy and portability. Consequently, there is significant interest in exploring new methods of pumping, as well as in translating them into miniaturized devices that can operate autonomously and can be integrated within microfluidic channels or chips, for achieving active fluid transport [1].

Patches of enzyme immobilized on surfaces have been shown to induce flow in the solution surrounding them, when the solution contains the corresponding substrate and the enzyme is catalytically active [2]. This finding has motivated several studies aimed at investigating their use as self-powered micropumping systems suitable to carry out various tasks within microfluidic channels. “Proof-of-principle” experimental studies of such micropumps have employed several types of enzymes: glucose oxidase (GOX) [2, 3], catalase [2, 3], urease [2, 4,5,6,7], lipase [2], acid phosphatase [3, 8], and DNA polymerase [9]. Although the enzyme micropumps are relatively new concepts, a number of applications based on them have been proposed, such as transport of microparticles between different points of a microchamber [6], or detection of toxic compounds [4]. Several insightful reviews have been devoted to such developments [10,11,12].

The flows generated by enzyme micropumps are usually documented by employing tracer microparticles and following their motion at several locations within the solution (see, e.g., Refs. [2, 7]). Starting with the studies in Refs. [2, 4], it has been argued that for enzymatic pumps the hydrodynamic flow is due to solutal buoyancy effects (see also Refs. [7, 13]); in other words, such micropumps stir the solution surrounding them by locally modifying its mass density. However, this is not necessarily the only mechanism at play. We have recently reported that, in low ionic strength solutions of glucose, silica tracer microparticles, sedimented very close to the wall on which a GOX enzyme micropump is imprinted, exhibit an effective repulsion by the enzyme patch [14]. It has been argued that this behavior, which is opposite to the expectation of tracers moving toward the chemically active patch by solutal buoyancy flows [4], is compatible with the scenario of tracers moving by diffusiophoresis and being dragged by the osmotic flows induced at the wall [14]. This is in line with the previous reports of significant electrophoretic and electroosmotic effects (without ruling out bulk driven solutal buoyancy flows, see Ref. [15]) for other types of micropumps; e.g., in the case of pumping by ion-exchange resins [16, 17], or in that of chemically active Pt patches imprinted on Au or silicon surfaces, which catalyzes the decomposition of hydrogen peroxide [18, 19]. (Similar important effects of osmotic flows have been also observed for systems driven out of equilibrium by other methods, such as thermoosmosis owing to local heating induced by light-absorbing Au nanoparticles glued to glass walls [20], or difussioosmosis due to a laser-induced, local cis-trans photo-isomerization of azobenzene molecules in aqueous solutions [21].)

The geometry of the system studied in Ref. [14], which can be well approximated as the liquid solution occupying a half-space, has the advantage of being amenable to detailed analytical calculations for simple models of chemically active patches [22]. However, from the perspective of applications in microfluidic systems, it is important to understand the robustness of the findings concerning the effective interaction experienced by silica tracer microparticles near a chemically active GOX enzyme micropump with respect to operation under geometrical confinement. Additional motivation for studying the impact of geometrical confinement on the operation of our GOX enzyme micropumps is provided by the findings, reported in Ref. [13], of significant qualitative changes in the hydrodynamic flow driven by enzymatic reactions within a closed cell upon decreasing the height of the cell.

Accordingly, here we report on the dynamics of silica tracers in the vicinity of chemically-active GOX enzyme micropumps, operating within experimental cells of planar slab geometry (see Fig. 1), upon varying the height H of the cell from values very large compared to the size of the enzymatic patch down to values comparable with the size of the patch. The experimental results evidence that the formation of a depletion zone around the enzymatic patch is a robust feature, independent of the height of the cell in the range of values H explored in the study. However, the dynamics of growth of the exclusion zone exhibits a dependence on the height of the experimental cell; while this dependence is significant at moderate concentrations (i.e., 0.1 mM) of glucose, it unexpectedly seems to vanish upon increasing the glucose concentration to \(\simeq 0.4~\text {mM}\). The results are discussed within the confines of a simple theoretical model of a chemically active enzyme patch.

Fig. 1
figure 1

Schematic representation of the experimental cell, which can be approximated as a planar slab of height H. The extent ΔR of the tracer depletion zone is measured from the edge of the enzyme patch (indicated by the central, green disk of radius R)

Full size image

Experimental materials and methods

Materials

GOX (Cat. No. G7141), glucose (Cat. No. G7021), bovine serum albumin (BSA, Cat. No. G4287), 3-aminopropyl-tri-ethoxysilane (APTES, Cat. No. A3648), glutaraldehyde (25%, Cat. No. G400-4), toluene (Cat. No. 244511), silica microparticles (3 μm in diameter, Cat. No. 66373), and glycerol (Cat. No. G7893) were purchased from Sigma Aldrich Inc. Acetone (min. 99.92%) and ethanol (min 99.5%) were purchased from the local distributor Chimreactiv SRL (Bucharest, Romania). High-precision microscope cover glasses (24 mm × 60 mm × 0.17 mm, Cat. No. 277684063, and 22 mm × 22 mm × 0.17 mm, Cat. No. 41022012) were purchased from Carl Roth GmbH. Borosilicate glass capillaries (100 mm × 1.5 mm × 0.86 mm, Cat. No. GC150F-10) were purchased from Harvard Apparatus. All (bio)chemicals have been used as received. All necessary solutions have been prepared with ultrapure water from a Millipore Direct-Q 3 UV water purification system.

Fabrication of enzyme micropumps

The GOX enzyme micropumps were fabricated by the method already described in detail in Ref. [14]; therefore, here we only succinctly summarize the main steps of the process. A microscope cover glass (24 mm × 60 mm × 0.17 mm) is washed with acetone and ethanol and subsequently modified with APTES by immersion into an APTES solution (5%, made in toluene) for 10 min. A GOX-based “ink” is prepared by mixing 2 parts of a GOX solution (50 g/L, prepared in an aqueous solution with 1% glycerol) with 1 part of a BSA solution (50 g/L, prepared in an aqueous solution with 1% glycerol). A glass micropipette (outer diameter of 190 μm, inner diameter 120 μm), made out of a borosilicate glass capillary, is then loaded by capillarity with few microliters of the GOX ink and subsequently brought into contact, five times, with the APTES-modified microscope cover glass. At each contact, a small volume of the GOX ink is transferred from the pipette onto the APTES-modified glass; the deposited GOX ink dries within 1–2 s. The enzyme patch, imprinted by using the procedure describe above, is then stabilized via cross-linking through exposure for 15 min to the vapors of a 25% aqueous solution of glutaraldehyde. In the final step of the fabrication, the cross-linked enzyme patch, typically of radius R ≈ 110 μm, is incubated for 15 min within an aqueous BSA solution (concentration 3.3 g/L). It turns out that the BSA not only consumes the residual, unreacted glutaraldehyde, but it also contributes to a significantly decreased adherence of the silica microparticles to the glass slide carrying the enzyme patch. Finally, before the start of an experiment, the micropump is thoroughly washed with water to remove any components which were not strongly anchored to the APTES- and BSA-modified glass slide.

Experimental setup and optical microscopy observations

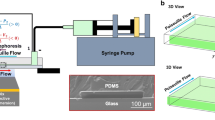
For the studies of the motion of tracers in the vicinity of chemically active GOX patches (see also Ref. [14]), the micropumps, fabricated according to the method described above, are inserted into a homemade experimental cell. The cell consists of a PDMS O-ring (with inner diameter 2L = 1 cm and height H = 2.2 mm, 1.6 mm, or 0.6 mm, respectively), which is placed over the glass slide with the enzyme micropump. The placement of the PDMS O-ring is such that the enzyme patch is located approximately in the center of the region enclosed by the ring. After filling the cell with the solution containing tracer microparticles and the selected concentration of glucose, the cell is covered with another microscope glass slide (22 mm × 22 mm × 0.17 mm). This not only provides the means for geometrical confinement, but it also reduces the water evaporation, and thus any spurious flows (not directly related to the activity of the enzyme pump). Owing to \(L/R~\simeq ~50 \gg 1\), the geometry of the experimental cell is well approximated by that of a (laterally infinite) planar slab of height H (see Fig. 1). For the control experiments with an “inverted” micropump geometry, the steps above are repeated, but starting with the microscope glass slide and completing the cell by covering it with the glass slide on which the enzyme patch is imprinted.

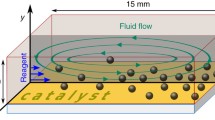
The tracer microparticles, sedimented at the bottom wall, are visualized through the bottom wall of the experimental cell by using an Observer D1 inverted microscope from Carl Zeiss AG equipped with an A-plan, 10×/0.25 Ph1 objective from the same company and with a DFK 31AF03 CCD camera from The Imaging Source Europe GmbH. For the illumination of the cell, a LED is employed as the light source in our microscope (which also contributes to reducing the heating of the cell and the water evaporation). The video recording at 2 frames/s is done using the Lucam Recorder as the image acquisition software, while the subsequent image analysis is carried out using ImageJ [23]. The radial extent Rd (see Fig. 1) of the region depleted of tracers (see, e.g., Fig. 2) is determined from the azimuthally averaged areal density of tracers as the midpoint of the transition between the regions of very low and large density, respectively.

Fig. 2
figure 2

Evolution of the depletion zone around a catalytically active GOX micropump in a solution containing 0.2 mM glucose. The height of the experimental cell is H = 1.6 mm

Full size image

Results and discussion

Formation of depletion zones around chemically active enzyme patches

Irrespective of the height H of the experimental cell, we observed that the silica tracer microparticles, which sedimented onto (but not adhered to) the lower glass wall of the experimental cell, on which the GOX patch is imprinted, experienced an effective repulsion when the GOX patch is chemically active. In other words, “depletion zones”, i.e., regions lacking tracer microparticles, emerge around catalytically active GOX micropumps; as shown in Fig. 2 (see also the next section), the size of the depletion zone increases in time for the whole duration (20 min) of the experiment. (We note here that the micropump remains active for significantly more than 20 min. The choice of 20 min as the maximum duration of recording is such that the largest depletion zone observed in the complete set of experiments, e.g., the right panel in Fig. 3, remains within the field of view of the microscope.) This behavior is in line with that observed in the case of “half-space” (height H/R ≫ 1) experimental cells [14].

Fig. 3
figure 3

Depletion zones produced by a GOX micropump at 20 min after turning the micropump on (by using a 0.2 mM glucose solution) in experimental cells of heights H of 0.6 mm, 1.6 mm, and 2.2 mm, respectively

Full size image

The impact of geometrical confinement on the time evolution of the depletion zone

As illustrated in Fig. 3, at concentrations of glucose ≤ 0.2 mM, we observed that upon reducing the height of the experimental cell (i.e., when the geometrical confinement by the slab is strengthened), the extent of the depletion zone generated by the GOX micropumps, under otherwise identical conditions, significantly decreases. At 20 min after the activity of the micropump was turned on (i.e., the glucose solution was added), the average (over three distinct experiments) radial extension ΔR of the tracer depletion zone (measured from the edge of the enzyme patch, see Fig. 1) decreases from 156 ± 17 μm, in an experimental cell of height H = 2.2 mm, to 128 ± 14 μm for H = 1.6 mm, and to 85 ± 11 μm for H = 0.6 mm.

From the video recordings of the experiments, one can determine the extent of the depletion zone as a function of time. The results are shown in Fig. 4 for the three values of the glucose concentration in experimental cells of three different heights H. While at glucose concentrations of up to 0.2 mM (Fig. 4a and b) the impact of geometrical confinement becomes significant once \(H/R \lesssim 6\), at the larger glucose concentration of 0.4 mM (Fig. 4c) there is no visible effect of the height of the cell on the dynamics of the depletion zone during the time span of the experiment. Additional experiments using a glucose concentration of 1 mM (results not shown) show a similar trend to that observed at 0.4 mM glucose, i.e., the dynamics seems independent of the confinement height H. (Unfortunately, at 1 mM glucose concentration, the reproducibility of the experiments at small H is significantly affected by an increased tendency of the silica tracers to adhere to the wall (the cause of this latter effect is unclear to us), and thus clear-cut conclusions cannot be drawn in this case.)

Fig. 4
figure 4

Time evolution of the depletion zones (radial extent measured from the edge of the enzyme patch) produced by active GOX micropumps operating at glucose concentrations of 0.1 mM (a), 0.2 mM (b), and 0.4 mM (c), respectively, in experimental cells of heights H = 0.6 mm (\(\square \)), 1.6 mm (∘), or 2.2 mm (Δ). The lines connecting the symbols are just a guide to the eye. The points represent the median, and the error bars the min to max spread, of values in three distinct realizations of the experiment (each involving a different enzyme patch)

Full size image

Discussion

The functioning of a catalytic patch pump relies on creating and sustaining a spatially non-uniform distribution of chemical species in the surrounding solution. This sources hydrodynamic flow in the solution via two effects, one being a spatially varying mass density of the liquid (due to the spatially varying chemical composition of the volume elements), see, e.g., Ref. [8], and the other one being an induced osmotic flow at the wall (due to the variations in chemical composition of the solution along the wall [24,25,26]). Since for catalytically active micropatches the induced flows are weak, they are well described by the zero-Reynolds number Stokes equations; consequently, one can write the flow as the superposition of a bulk (solutal buoyancy [8]) driven one with no-slip at the walls, \(\vec {v}_{b}\), and an osmotic-driven one with no sources in the bulk, \(\vec {v}_{o}\).

The rate of growth of the radial extent of the depletion zone, when its radius is Rd, is given by the velocity of a tracer particle at Rd. Approximating, for simplicity, the monolayer of tracers as being sufficiently dilute (single particle limit), the velocity \(\vec {v}_{tr} (R_{d})\) of a tracer is simply given by the superposition of three contributions. These are as follows: (i) phoretic response, \(\vec {v}_{ph} (R_{d})\), to the gradients in the composition of the solution (“chemical field”) at the location Rd of the tracer; (ii) drag by osmotically driven flow, \(\vec {v}_{o}(R_{d})\), induced by the gradients in the chemical field along the wall; and (iii) drag by the bulk-driven flow, \(\vec {v}_{b} (R_{d})\), driven by the spatial variations in the mass density of the solution induced by the chemical field. Accordingly, once the chemical field is known, the velocity of a tracer at a given location Rd, \(\vec {v}_{tr} (R_{d}) = \vec {v}_{ph} (R_{d}) + \vec {v}_{o}(R_{d}) + \vec {v}_{b} (R_{d})\), is known and the overdamped dynamics of the tracer, \(d \vec {R}_{d}/dt = \vec {v}_{tr} (R_{d})\), can be integrated to determine the time dependence of the depletion zone [14].

Before proceeding, we note that isolating each of the three velocity components discussed above, and estimating their relative magnitude (which may be expected to differ at different locations, i.e., near or far from the walls), is in general very challenging. In what concerns the formation of the depletion zone in our system, in which the silica particles are sedimented very near to the glass wall due to the large density mismatch with the aqueous solution, we have previously argued that the contribution from the bulk-driven solutal buoyancy flow is expected to be sub-dominant [14]. Further arguments in support of this expectation follow by comparing the behavior exhibited by tracers at the bottom wall of the cell in “upright” (active patch at the bottom wall) and “inverted” (active patch at the top wall) setups. As shown in Fig. 5, in the inverted setup, there is no indication of the formation of a tracer-exclusion zone. In the light of the very recent study in Ref. [27], this result is interpreted as follows. It has been shown in Ref. [27] that the solutal buoyancy flow induced by a disk-like active patch in a strongly confined geometry (i.e., a cell with H/L ≪ 1 in the context of our experiments) can be approximated by the Stokes flow due to the lateral variations of the cross-section (vertically) averaged mass density of the solution. The theoretical prediction was shown to provide a very good fit for the experimentally measured velocity profiles induced by a chemically active silver patch decomposing hydrogen peroxide in aqueous solution [27]. Due to the vertical-averaging of the density, the predicted flow is invariant with respect to the active patch being located on the bottom or on the top wall [27]. Translating the latter finding to our study, it implies that the drag by solutal buoyancy flow cannot be dominant contribution in the formation of the tracer depletion zone: if it would be, then a tracer depletion zone would emerge also in the inverted configuration, an implication which is in contrast to the experimental results (Fig. 5).

Fig. 5
figure 5

Distribution of tracers sedimented at the bottom wall of an experimental cell of height H = 0.6 mm at 20 min after turning on the activity of the GOX micropump. The results shown correspond to the active patch being located at the bottom wall (left column) or at the top wall (right column), respectively, as shown by the schematic drawings in the top row, and to solutions of glucose concentration 0.1 mM (middle row) and 0.2 mM (bottom row), respectively

Full size image

Irrespective of their relative magnitudes, all the three contributions discussed above have the same source, which is the spatially (and, in general, also temporally) varying chemical composition of the solution. It is therefore reasonable to expect that the effects of the spatial confinement observed in experiment are a reflection of changes in the chemical field upon varying H. Accordingly, we will focus the rest of the discussion on the issue of calculating the chemical field.

The calculation of the distribution of reactants and reaction products by diffusion in the presence of the sink (for reactant) and source (for product) chemical patch can be simplified under several assumptions. First assumption is that the number densities of the reactant and product species remain sufficiently small (over time scales relevant to the experimental ones) such that the mixture of solvent, reactants, and products behaves as a dilute, ideal solution (i.e., the solute species can be treated as ideal gases). Second assumption is that the transport of the solutes by diffusion dominates their advection by the ambient flow \(\vec {v}_{b} + \vec {v}_{o}\). Finally, it is assumed that the reaction scheme is sufficiently simple as to avoid non-linear coupling between the densities of reactants and that reactants are present in abundance, such that their average (bulk) density is basically unaffected by the consumption at the active patch.

For our system, the relevant enzyme-catalyzed process is the transformation of glucose into gluconolactone according to the reaction scheme:

$$ \mathrm{ C_{6} H_{12} O_{6} + O_{2} \longrightarrow C_{6} H_{10} O_{6} + H_{2} O_{2} . } $$
(1)

In the following, we assume that O2, which is a fast diffusing molecule (diffusion coefficient \(\sim 2 \times 10^{-9}~\mathrm {m^{2} s^{-1}}\) in water at room temperature [28]), remains always well mixed (i.e., uniform, constant number density) within the reaction volume. Therefore, concerning the distribution of reactants only the diffusion of the glucose, C6H12O6 (diffusion coefficient \(\sim 0.7 \times 10^{-9}~\mathrm {m^{2} s^{-1}}\) in water at room temperature [29]), will be considered here. Based on the results in Ref. [14], the kinetics of the enzymatic reaction in Eq. 1 is in the linear regime in the range of glucose concentrations, cg ≤ 0.4 mM, employed in this study. Accordingly, the number density current of each product species released at the patch can be written as K = kcg, with cg denoting the local concentration of glucose and k being a constant with units of velocity. (The number density current of reactant removed in the reaction is given by the same expression, but with opposite sign.)

Under all these assumptions, the distributions of the reactant and product species in the domain enclosed by the planes z = 0, which contains an active disk region of radius R centered at origin, and the plane z = H, obey the diffusion equations:

$$ \partial_{t} c_{j}(\vec{r},t) - D_{j} \nabla^{2} c_{j}(\vec{r},t) = 0 , $$
(2)

subject to the initial condition:

$$ c_{j}(\vec{r},t = 0) = C_{j} , $$
(3a)

and to the boundary conditions:

$$ c_{j}(|\vec{r}| \to \infty,t) = C_{j} , $$
(3b)
$$ ~\vec{e}_{z} \cdot [- D_{j} \nabla c_{j}(\vec{r},t)]|_{z = H} = 0 , $$
(3c)

and

$$ \vec{e}_{z} \cdot [- D_{j} \nabla c_{j}(\vec{r},t)]|_{z = 0} = \begin{cases} &\alpha_{j} K ,~\text{if}~|\vec{r}| < R\\ & 0 ,~\text{otherwise} \end{cases} . $$
(3d)

In these equations, the index j refers to any of the products or to the glucose (case in which j ≡ g), Cj denotes the bulk density of the species j (for our system, the bulk density of products is vanishing, and only Cg≠ 0), and αj = 1 (source) for products, while αg = − 1 (sink) for glucose, Dj denotes the diffusion coefficient of the species j, and \(\vec {e}_{z}\) is the unit vector of the z-direction. The diffusion problems defined by Eqs. 2 and 3 are, in general, difficult to solve analytically; thus, one has to rely on numerical calculations, a task that we leave for future work. However, certain qualitative features, which can be inferred from particular cases, provide insight on the effect of the confinement on the distributions of number densities; this allows us to propose a plausible explanation for some (but not all) of the experimental observations as follows.

The case in which \(H \to \infty \), i.e., a half-space geometry, has been analyzed in Ref. [14] for the steady-state distribution of the products in the limit of reaction limited kinetics (i.e., when the Damköhler number is very small and thus \(c_{g}(\vec {r},t) \simeq C_{g}\)). It has been concluded that the spatial extent of this distribution is represented, roughly speaking, by a region of radius 10R – 15R, centered around the active patch of radius R. The density of product in the plane z = 10R is ≈ 5% of the maximum density value, which is attained right above the center of the active patch; the density of product decreases to less that 1% of that value when considering the plane z = 15R. This means that the density distribution in a slab with \(H/R \gtrsim 10\) is basically insensitive, at all times t, to the confinement condition, Eq. 3c, at the plane z = H; it is thus well approximated by the half-space state solution (as long as the limit of reaction limited kinetics holds). Accordingly, the source driving the dynamics of the depletion zone is insensitive to the value of H if \(H/R \gtrsim 10\). For the experimental cells with H = 2.2 mm and 1.6 mm, respectively, the parameter H/R takes the values \(H/R \simeq 20\) and \(H/R \simeq 14.5\), respectively, and this explains why there are only small, though noticeable, differences between the dynamics of the depletion zone at these parameters (see Fig. 4).

Accordingly, effects of the confinement may, in principle, be significant in the case of the experimental cell with the smallest height H = 0.6 mm, which corresponds to \(H/R \simeq 5.5\). For finite H, it is known that Eqs. 2 and 3 do not allow steady state distributions (see, e.g., Refs. [30,31,32]); therefore, it is necessary to first assess if the confinement is relevant at the time scales relevant to the experiment. One can estimate the relevance of the confinement simply by recalling that a characteristic size connected to the three-dimensional diffusion from a source is \(L_{D} = \sqrt {6 D t}\), where t is the time (since the source is active) and D the diffusion coefficient. The condition LD = H leads to the crossover time t0 = H2/(6D): for t < t0 the diffusion is basically unaffected by confinement, while for t ≫ t0 the effects of the confinement cannot be neglected. Considering the diffusion of the faster molecular product species (H2O2), one has \(D \sim 10^{-9}~ \mathrm {m^{2}/s}\); thus, for H = 0.6 mm one arrives at the estimate \(t_{0} \sim 60\) s, which indeed is deep within the time span of the experiment. Accordingly, at this value of H, the confinement may have significant effects on the chemical field.

The arguments above clarify that, in the case of the experimental cell of smallest height, it is necessary to solve the diffusion problems, Eqs. 2 and 3, for the time-dependent solutions [30, 32]. The question then arises if the slowing down of the expansion of the depletion zone can be just a consequence of the time evolution of the density of products and reactants (which, implicitly, means that in the right hand side (rhs) of Eq. 3d one accounts for the spatial and time dependence of the glucose concentration over the enzyme patch). When H is finite, (2) and (3) lead to effectively quasi two-dimensional diffusion problems (see, e.g., Refs. [30,31,32]). Therefore, one can employ the results known about diffusion from a source in two dimensions (see, e.g., Ref. [32]), to infer that around the enzymatic patch a region depleted of reactants emerges, the extent of which grows in time like \(\sqrt {t}\) (eventually crossing over to a \(\ln (t)\) dependence at long times). This can be interpreted—in a rough approximation—as if the enzyme pump effectively operates without spatial confinement but the patch is exposed to an ambient substrate concentration smaller that the nominal, bulk value. This would lead to the tracer depletion zone following the slower dynamics of the reduced effective value of the concentration, rather than the dynamics corresponding to the bulk concentration; this provides a simple, intuitive explanation for the slowing down observed in the experiments at 0.1 and 0.2 mM glucose concentrations (Fig. 4a and b).

On the other hand, the behavior at the higher bulk concentration of glucose, where no effects of confinement are observed for H = 0.6 mm (see Fig. 4c), cannot be accounted for by the mechanism discussed above. By considering (3d), one immediately infers that a characteristic density Cch = kCgR/Dg factors out from the diffusion problems of all species (because of the linearity of the equations). Accordingly, the density of products and reactants (solutions of the corresponding (2) and (3)) can be written as \(c_{j}(\vec {r},t)/C_{ch} = F(\vec {r},t;H/R,D_{j}/D_{g})\). This means that the spatial distribution of products, which is given by the function F, is independent of Cg. Consequently, the prediction is that at each fixed bulk concentration of glucose one should observe qualitatively the same changes in the dynamics of the tracer depletion zone upon varying H, which clearly contradicts the experimental findings (see Fig. 4). Furthermore, it also implies that at fixed value of H a collapse onto an universal curve should be observed if the dynamics of the tracer depletion zone is rescaled by the bulk concentration of glucose. While this reasonably holds for the dynamics in a half-space (\(H \to \infty \)) setup (see Ref. [14]), Fig. 6 (which is just a different representation of the data from Fig. 4) allows one to clearly infer that such a data collapse does not hold in the case of the confined suspension (e.g., the rates of growth in Fig. 6a are clearly not obeying the ratio 1:2:4). Furthermore, the deviations from such rescaling depend also on the confinement (e.g., compare the data at 0.1 and 0.2 mM glucose concentrations in Fig. 6 panels a and b).

Fig. 6
figure 6

Time evolution of the depletion zones (radial extent measured from the edge of the enzyme patch) produced by active GOX micropumps in experimental cells of heights H = 0.6 mm (a), 1.6 mm (b), and 2.2 mm (c), respectively, operating at glucose concentrations of 0.1 mM (\(\square \)), 0.2 mM (∘), or 0.4 mM (Δ). The lines connecting the symbols are just a guide to the eye. The points represent the median, and the error bars the min to max spread, of values in three distinct realizations of the experiment (each involving a different enzyme patch)

Full size image

Since the conclusion above follows from quite general considerations, the resolution of the issue of dependence on Cg requires re-examination of the—relatively standard—model, Eqs. 2 and 3. Invoking a product non-linearity in the flux (rhs) of Eq. 3d, by involving also the O2 distribution as an additional space- and time-dependent density field of reactant, does not solve the issue because Cch still factors out as a density scale. One possibility that cannot be a priori ruled out is that the approximation of a fixed bulk concentration breaks down. This could be the case if the consumption of the reactants during the time of the experiment is a significant fraction of the initially present concentration in the experimental cell (which is a closed system). However, this remains a speculation that requires significant additional work in order to understand whether or not it can provide a consistent argument for the behavior revealed by the experiments.

Conclusions

In this study, the effect of geometrical confinement in a planar slab on the operation of micropumps, consisting of catalytic GOX enzyme patches imprinted on a wall and exposed to an aqueous solution of glucose, has been evidenced via the response of silica tracer particles located near the active patch. As discussed in “Formation of depletion zones around chemically active enzyme patches” and “The impact of geometrical confinement on the time evolution of the depletion zone,” the systematic outward motion of the tracer particles leads to the formation of a zone depleted of tracers, which is an experimentally accessible observable. The dynamics of the depletion zone is due to three possible contributions to the motion of tracers: phoresis, drag by osmotic flows, and drag by bulk-driven (solutal buoyancy) flows; for our system, we have shown (see “Discussion” and Fig. 5) that the latter seems to be sub-dominant. All these three contributions have the same source, which is the spatially non-uniform distribution of product and reactant species (chemical field) emerging due to the chemical activity of the patch. Accordingly, changes in the dynamics of formation of the zone depleted of tracers should correlate with changes in the chemical field. This line of arguments has been exploited in “Discussion” to infer qualitative features of the chemical fields corresponding to a simple model of a chemically active patch and to correlate them with the experimental observation.

Summarizing the experimental study and the analysis in “Results and discussion,” the following conclusions can be drawn:

  • (i) Irrespective of the strength of confinement, silica tracer microparticles, sedimented onto the glass wall carrying a GOX micro-patch, are repelled by the GOX micro-patch when this is active in low ionic strength solutions of glucose. The repulsive interaction leads to the formation of a depletion zone lacking tracer particles in the close vicinity of the GOX micro-patch, which is a robust result with respect to variations in the strength of the confinement.

  • (ii) At a low concentration of glucose, stronger geometrical confinement (i.e., smaller H) induces a slower growth of the tracer depletion zones. Surprisingly, as the concentration of glucose is increased to 0.4 mM, this effect seems to disappear.

  • (iii) A plausible explanation for the slower dynamics of the tracer depletion zone, when the GOX micro-patch is confined, is that of an unavoidable reactant-depletion at the catalytic patch due to the diffusion under confinement being essentially time-dependent and quasi two-dimensional. However, the dependence of the magnitude of the effects on the bulk concentration of glucose (Fig. 4) remains a puzzle that requires further studies.

The effects discussed above, and in particular the rather surprising lack of confinement effects on the pump operation at moderate to large bulk concentrations of glucose, could be important for development of microfluidic enzymatic pumps. This provides additional motivation for further work aiming at an in-depth theoretical understanding of these features and, in general, of the operation of chemically active patches under confinement.