1 Introduction

The global radiative fluxes at the top of atmosphere (TOA) include the incoming and reflected shortwave radiation and the outgoing longwave radiation. Over recent decades there has been energy accumulating in the climate system since absorbed sunlight has been on average greater than outgoing longwave radiation and this is causing the planet to warm, sea levels to rise and the water cycle to change (Easterling and Wehner 2009; Knight et al. 2009; Trenberth and Fasullo 2013; Huber and Knutti 2014; Watanabe et al. 2011; von Schuckmann et al. 2020). The surface energy budget includes downward and upward surface shortwave and longwave radiative fluxes and the latent heat (evapotranspiration) and sensible heat turbulent fluxes. The asymmetric hemispheric distribution of the net downward TOA radiative flux and the net surface flux are closely related to cross-equatorial energy transports in both atmosphere and oceans (Loeb et al. 2018b; Liu et al. 2017), as well as the position of the intertropical convergence zone (ITCZ) (Donohoe et al. 2013; Frierson and Hwang 2012; Kang et al. 2018; Liu et al. 2020). More than 90% of the energy accumulating in the Earth system is taken up by the ocean (Cheng et al. 2017). The energy absorbed by the top layer ocean is the key factor determining the surface temperature variability (Easterling and Wehner 2009; Knight et al. 2009; Trenberth and Fasullo 2013; Su et al. 2018), and the energy entering the deeper ocean can accumulate and affect long-term climate change (Otto et al. 2013; Richardson et al. 2016). Therefore, it is essential to accurately observe and understand present day changes in energy fluxes at the TOA and the surface.

CERES (Clouds and the Earth’s Radiant Energy System) provides high quality TOA radiative flux data since March 2000 (Loeb et al. 2012; Kato et al. 2013) and the data since 1985 prior to CERES has been reconstructed by Allan et al. (2014) using the satellite observations of ERBE WFOV (Earth Radiation Budget Experiment Satellite wide field of view, 72 day mean) (Wong et al. 2006) and ECMWF ERA-Interim reanalysis (Dee et al. 2011; Berrisford et al. 2011). Discontinuities in the reconstruction were dealt with using the 5th Atmospheric Model Intercomparison Project (AMIP5) simulations and other high resolution atmospheric model simulation results. The net surface fluxes have also been estimated by the residual method (Trenberth and Solomon 1994; Mayer and Haimberger 2012; Liu et al. 2015, 2017) in which mass corrected horizontal transport of atmospheric energy and atmospheric energy accumulation from ERA-Interim reanalysis are combined with net TOA fluxes. The reconstructed TOA fluxes and estimated net surface energy fluxes have been used in various studies (Williams et al. 2015; Valdivieso et al. 2015; Senior et al. 2016; Roberts et al. 2016, 2017; Mayer et al. 2016, 2018; Hyder et al. 2018; Mignac et al. 2018; Cheng et al. 2019; Trenberth et al. 2019; Bryden et al. 2019) for comparison with other data sets, model evaluation and understanding climate change and variability. The TOA radiative fluxes from CERES and ERBE WFOV have been updated recently and a more accurate method calculating the total atmospheric energy transport has been proposed (Mayer et al. 2017). In this paper an update of these estimates is provided and the variability in radiative fluxes since 1985 is quantified, considering cross-equatorial atmospheric and oceanic heat transports, the meridional heat transport at 26° N in the Atlantic and the heat transport from ocean to land.

2 Data and method

Following Mayer et al. (2017) and Liu et al. (2017), the net downward surface flux \({F}_{S}\) can be written as

$$ F_{S} = F_{T} - \frac{\partial E}{{\partial t}} - \nabla \cdot \frac{1}{g}\mathop \int \limits_{0}^{{p_{s} }} \left[ {\left( {1 - q_{g} } \right)C_{a} \left( {T - T_{o} } \right) + L_{v} \left( T \right)q_{g} + \varphi + k} \right]{\varvec{v}}dp $$
(1)

where \({F}_{T}\) is the net downward radiative flux at TOA. \(E\) is the total column atmospheric energy and \(\frac{\partial E}{\partial t}\) is its tendency. \({L}_{v}\) is the latent heat of condensation of water, qg is the specific humidity, Ca is the specific heat capacity of air at constant pressure, T is air temperature (relative to reference temperature T0), φ and k are geopotential and kinetic energy, respectively. \({\varvec{v}}\) is the horizontal wind velocity vector, and \(p\) is the air pressure. \({p}_{s}\) is the surface pressure. The last term on the right side of Eq. (1) is the divergence of atmospheric moist static plus kinetic energy transport, where enthalpy of atmospheric water vapor has been removed. This avoids inconsistencies arising from the non-zero atmospheric lateral total (dry plus moist) mass flux divergence, which balances surface freshwater flux (i.e. precipitation minus evaporation). Enthalpy of precipitation and evaporation usually are neglected, consequently leading to ambiguities in energy budget calculations if enthalpy of water vapour in the lateral transports is retained. These are particularly large when using the Kelvin temperature scale that is common in atmospheric science, as discussed in detail by Mayer et al. (2017). Trenberth and Fasullo (2018) acknowledged the reduction of ambiguities when changing to Celsius scale (i.e. setting T0 = 273.15 K, which reduces the magnitude of the error pattern arising from inconsistent treatment of vapor enthalpy by more than 90%, but in this context invoked the need for knowledge of the vertical profile of the temperature at which condensation occurs. This seems a relevant argument when dealing with entropy budgets, but here we are concerned with total energy, which is unaffected by phase changes as long as the mass budget is closed. Hence, use of the equations proposed by Mayer et al (2017) is deemed appropriate here. The effect of removing atmospheric vapour enthalpy from the budget equations will become evident in the discussion of cross-equatorial energy transports discussed in Sect. 3.2. All variables used in Eq. (1) are from ERA-Interim reanalysis, which is a four-dimensional variational analysis assimilating the full observing system (Dee et al. 2011).

The net surface energy fluxes can be estimated by combining the TOA radiative fluxes, and the atmospheric energy transport and tendency (Trenberth 1991; Trenberth et al. 2001; Mayer and Haimberger 2012; Liu et al. 2015, 2017). The atmospheric energy transport (or convergence/divergence) is usually taken from atmospheric reanalyses, since they represent the atmospheric state including wind patterns realistically due to the large amount of observational data being assimilated. However, the imbalance of the wind-induced mass transport and surface pressure changes, which arises from the lack of observational constraint of divergent winds, necessitates a mass correction to the atmospheric transport (Trenberth et al. 2009; Mayer and Haimberger 2012; Liu et al. 2015). The total atmospheric energy transport is re-calculated following Mayer et al (2017) by removing the enthalpy of the water vapour from the atmospheric energy transport, and the net surface energy fluxes are derived based on procedures of Liu et al. (2017) who proposed a land surface flux adjustment based on an upper soil layer energy budget approach. This is still needed for the updated atmospheric transport of Mayer et al. (2017) to ensure a physically reasonable multiannual mean land surface energy budget (Liu et al. 2015, 2017), which means the regional land surface surface flux changes are based on a modelling rather than observational approach. The mean net land surface flux is now anchored to a new estimate of 0.2 W m−2 (equivalent to about 0.06 W m−2 for the global surface area) over 2004–2014 using years where a minimum of 50 ground heat flux measurement sites are available (Gentine et al. 2019) rather than 0.08 W m−2 over 1985–2012 applied in previous studies (Liu et al. 2015, 2017).

The multiannual mean TOA net radiative flux is anchored to 0.71 W m−2 over 2005–2015 (Johnson et al. 2016), with 0.61 ± 0.09 W m−2 taken up by the ocean from 0–1800 m, 0.07 ± 0.04 W m−2 by the deeper ocean and 0.03 ± 0.01 W m−2 by melting ice, warming land, and an increasingly warmer and moister atmosphere. The multiannual mean (2006–2013) ocean heat storage (0–2000 m) in southern and northern hemispheric oceans, the zonal mean ocean heat storage in the global ocean and Atlantic, and the time series of ocean heat storage are all calculated from the five ensemble members of ECMWF’s ORAS5 (Ocean ReAnalysis System 5) reanalysis (Zuo et al. 2019), with the adjustment of OHCT (Ocean Heat Content Trend) based on the global mean surface heat flux into the ocean (see Sect. 3.2 for details). ORAS5 is a state-of-the-art eddy-permitting ocean reanalysis running on ¼° degree resolution. It has been found to provide realistic variability in ocean heat storage and oceanic transports in the tropics (Mayer et al. 2018; Trenberth and Zhang 2019) and the Arctic (Uotila et al. 2019; Mayer et al. 2019), but it seems to overestimate decadal variability in the North Atlantic (Jackson et al. 2019). The eddy transport is a crucial component of heat transport and the eddy parameterization (Gent and McWilliams 1990) may not represent such effect well, which may be a limitation of this method. The RAPID time series at 26° N (Smeed et al. 2017) and some of the newly published ERA5 (the fifth generation ECMWF ReAnalysis) data (Hersbach et al. 2020) are also employed for comparisons. All data sets and brief descriptions are listed in Table 1.

Table 1 Datasets
Full size table

Following Allan et al. (2014), the TOA fluxes since 1985 and prior to the CERES era have been reconstructed based on ERA5 reanalysis anomaly spatial distribution constrained by the low resolution ERBE WFOV variability and CERES climatology. We use the recently updated CERES EBAF version 4.1 (Loeb et al. 2018a). An update of the ERBE WFOV v4.0 dataset (Shrestha et al. 2019) was also considered but an apparently unrealistic increase in interannual variation after the discontinuity in 1993 (see Figure S1), primarily attributed to absorbed solar radiation (ASR), led us to retain the validated v3.0 product. However, the data in 1999 are not used due to their low frequency of observations (Shrestha et al. 2019). The anomalies over gaps around 1993 and 2000 are filled by interpolating radiative flux anomalies from ERA5 following Liu et al. (2015). The absolute values on both sides of the gaps are adjusted based on the ensemble mean from ten AMIP6 (the sixth phase of the coupled model intercomparison project) model simulations (Eyring et al. 2016) listed in Table 1. Unlike in the previous versions where only the hemispheric constraint was applied, the grid point information of the ERBE WFOV data are used in this study to constrain the TOA flux at 10° × 10° resolution. The CERES radiation fluxes from March 2000 onwards are then combined to form a complete data set (DEEPC v4.0) from January 1985 to January 2019 based on the available CERES observations.

The resulting time-series of the reconstruction are sensitive to the number of years considered prior to and following each of the two data gaps. A shorter period introduces additional noise to the time series while a longer period aliases more of the simulated variability into the reconstructed dataset. A pragmatic approach is therefore required in which the advantages and disadvantages are balanced. While Allan et al. (2014) estimated an uncertainty based on the ensemble of simulations used, we further evaluated the sensitivity to the interpolation data length in more detail. The multi-month mean difference between both sides of the gap (the mean before the gap minus the mean after the gap) was calculated first for both reconstructed TOA flux (d1) and AMIP6 model ensemble mean (d2)(see Table S1), then the adjustment d = d1—d2 was calculated. The net radiative flux (NET) adjustment tends to be stable after two and a half years for the 1999–2000 gap and 2 years for the 1993–1994 gap (Figure S2). For absorbed solar radiation (ASR), the adjustments show similar characteristics. Therefore, the 3 years mean difference before and after the data gap is used for the adjustment, more than the 2-years chosen by Allan et al. (2014). By combining the variability between 2 and 3 years mean adjustment, the AMIP6 spread and the uncertainty of ± 0.1 W m−2 over the CERES period (Johnson et al. 2016) in quadrature, the corresponding uncertainty at 90% confidence level is ± 0.22 W m−2 over 1994–1999, ± 0.87 W m−2 over 1985–1993 and 0.61 W m−2 over 1985–1999 for NET TOA radiation flux (see supplementary for details). The estimated increase in Earth’s energy imbalance of 0.52 W m−2 from 1985–1999 to 2000–2016 is about the same magnitude as the estimated homogeneity adjustments uncertainty at the 90% confidence level. However, when combining this information with independent evidence of an increase in the rate of ocean heat content increase (Cheng et al. 2017), there is high confidence that Earth’s energy imbalance has been increasing since 1985.

Following the method of Loeb et al. (2016) and Trenberth et al. (2019), the ocean heat divergence (\(\nabla \cdot {F}_{O}\)) can be calculated by

$${F}_{d}-\mathrm{OHCT}=\nabla \cdot {F}_{O}$$
(2)

where Fd = Fs—Fice is the energy entering the ocean, Fice is the sea ice melting energy. The northward meridional ocean heat transport at latitude θ can be calculated by integrating Eq. (2) from the north (or south) pole to θ. The sea ice data are from the five ensemble members of ORAS5 which is in reasonable agreement with other estimates in the Arctic Ocean domain (Mayer et al. 2019). The time series of twelve month running mean global mean sea ice melting energy (positive for melting and negative for freezing) shows large interannual variability (Figure S3a) (Trenberth and Zhang 2019), but the uncertainty range from five ORAS5 ensemble members is relatively small. The global mean OHCT time series from ORAS5 for different depth integrations are plotted in Figures S3b-e (black line), together with the time series of TOA net radiative flux (FT) and the surface heat flux into the ocean (Fd). The shading denotes ± one standard deviation of five ORAS5 ensemble members and all lines are twelve month running mean. It can be seen that the variability of 0–300 m OHCT has good agreement with FT and Fd before 2005, and the correlation coefficients are about 0.73 and 0.69, respectively. The OHCT became lower after 2005. For other depth integrations, both absolute value and variability of OHCT have good agreement with FT and Fd before 1999, but large discrepancies occurred over 1999–2005 as discovered by Trenberth and Zhang (2019), when the observing system is transitioning from mainly XBTs (expendable bathythermographs) to mainly Argo floats (Chambers et al. 2016). The general agreement in both absolute value and the variability between OHCT and TOA FT further suggests the robustness of our reconstruction of FT over 1985–1999. In this study, the OHCT is integrated over 0–2000 m. To ensure energy conservation, the OHCT is adjusted by constraining its annual and global mean to the corresponding annual and global mean of Fd as shown by the cyan line in Figure S3d.

3 Results

3.1 Global mean TOA radiation fluxes and their variability since 1985

The global mean monthly anomaly (reference period is 2001–2005) time series of TOA fluxes are plotted in Fig. 1 for DEEPC v4.0, CERES Ed4.1, the AMIP6 model ensemble mean (gray shading denotes the ± 1 standard deviation of the ten simulations), ERA5 and ERBE WFOV v3.0. All lines are three month running means, while the ERBE WFOV data are 72 days means and are deseasonalized with respect to the 1985–1999 period, so the whole ERBE WFOV anomaly line is shifted vertically for clarity. An increasing trend in the NET flux (2001–2014) simulated by the AMIP6 model ensemble (0.12 ± 0.09 W m−2 decade−1) is insignificant and is about one third of the CERES observed estimate (0.34 ± 0.15 W m−2 decade−1 and is significant) while interannual variability is moderately well captured (correlation coefficient r = 0.51). The differences between two sets of CERES data are mainly from the improvement in the instrument calibration, cloud properties, angular distribution models for radiance-to-flux conversion and short time interpolation (Loeb et al. 2018a). The absolute NET flux of 0.71 W/m2 over 2003–2016 (same as CERES Ed 4.1) is used for the anchoring of net TOA flux, and the multiannual mean NET fluxes are 0.10 ± 0.61 W/m2 over 1985–1999 and 0.62 ± 0.10 W/m2 over 2000–2016 which is qualitatively consistent with the results of Cheng et al. (2017). It is noted that for both ASR and OLR, the updated reconstruction on both sides of the 1993 gap displays a smaller difference than that of ERBE WFOV due to the adjustment effect based on AMIP6 ensemble mean, and the OLR anomaly from the reconstruction is higher than that of AMIP6 ensemble mean before 1991. There is consistent variability between CERES and ERA5 before 2013 (r ≥ 0.77) but ERA5 does not capture the increase in NET and ASR after this (Fig. 1a, c) (Loeb et al. 2020); the reason behind this merits further investigation. The trends of NET, ASR and OLR from each data set and correlations between DEEPC and other data sets over 1985–2000 and 2001–2014 are listed in Table 2 for reference.

Fig. 1
figure 1

Deseasonalized monthly mean TOA radiation fluxes in W m−2 (reference period is 2001–2005). a Net radiation (NET), b outgoing longwave radiation (OLR) and c absorbed shortwave radiation (ASR). The 5 years mean values of NET downward fluxes are displayed at the top. Three month running means are applied. The WFOV data are 72 day mean and are deseasonalized with respect to the 1985–99 period, the corresponding lines are shifted vertically for clarity. Gray shading denotes the ± one standard deviation of the ten AMIP6 simulations

Full size image
Table 2 TOA flux trend (W m−2 decade−1) and correlation coefficient
Full size table

Although the variability of ERA5 and DEEPC OLR anomalies is in good agreement before (r = 0.79) and after 2000 (r = 0.87), OLR from DEEPC is up to 0.5 W m−2 lower than that of ERA5 and AMIP6 simulations between 1998 and 2002 (Fig. 1b). Following the Mount Pinatubo eruption in 1991, OLR decreases by nearly 2.5 W m−2 in 6 months in DEEPC and ERBE WFOV which is larger than the decrease in AMIP6 and ERA5 of about 1.5 W m−2. This may reflect inadequacies in simulating the effects of volcanic aerosol on longwave radiative transfer or unrealistic cloud structure and stratospheric thermal responses but is beyond the scope of the present study. The agreement of variability in ASR anomalies between DEEPC and ERA5 is generally good (Fig. 1c, r = 0.77), except that the CERES has a more positive trend. The DEEPC net flux is less positive than the AMIP6 ensemble by 0.47–0.95 W m−2 based on comparisons over multiple 5 year periods (Table 3), which can be explained by the lower simulated OLR. ERA5 overestimates both OLR and ASR by about 2 W m−2 compared to DEEPC, but they compensate each other to yield reasonable net flux agreement with observations.

Table 3 Five year mean TOA fluxes (W m−2)
Full size table

3.2 Global meridional energy transports and their variability

The hemispheric energy imbalances in both atmosphere and oceans are re-evaluated using the latest CERES radiation fluxes, updated net surface energy fluxes and adjusted ORAS5 0–2000 m OHCT (Fig. 2), and the geodetic weighting and the number of days in a month are also applied (Liu et al. 2017). The net downward radiation flux at TOA is 0.36 ± 0.04 PW in the southern hemisphere and − 0.01 ± 0.04 PW in northern hemisphere, so the southern hemisphere is gaining energy while the northern hemisphere is close to balance at the top of the atmosphere, consistent with previous work (Loeb et al. 2016; Irving et al. 2019; Lembo et al. 2019a).

Fig. 2
figure 2

Updated observations of hemispheric energy flows in the climate system in petawatts (PW) over 2006–2013. TOA radiative flux is from CERES EBAF 4.1 anchored to 0.71 W m−2 over 2006–2013. 0.01 PW is the heat absorbed by the atmosphere. The heat storage is 0.29 ± 0.02 PW in the southern hemisphere ocean and 0.06 ± 0.01 PW in the northern hemisphere ocean based on the ensemble mean of adjusted 0–2000 m ORAS5 OHCT

Full size image

At the surface, the net downward energy flux is 0.79 ± 0.16 PW in the southern hemisphere, driving ocean heating of 0.29 ± 0.02 PW. However, a strong northward transport of heat by the ocean (0.50 ± 0.16 PW), inferred from the surface heat fluxes and oceanic energy storage, transports much of this energy to the northern hemisphere where a small amount accumulates (0.06 ± 0.01 PW) but much is fluxed into the atmosphere above (0.44 ± 0.16 PW). The ocean heat transport is dominated by the Atlantic Meridional Overturning Circulation (MOC) transporting warm water northward across the equator to compensate for the southward export of colder North Atlantic Deep Water (Garzoli and Matano 2011; Mignac et al. 2018). These inferred transports are higher than our previous estimations (Liu et al. 2017) (0.22 ± 0.15 PW for southward atmospheric transport and 0.32 ± 0.16 PW for northward oceanic transport), and estimations of Stephens et al. (2016) (0.33 ± 0.6 PW for southward atmospheric transport and 0.45 ± 0.6 PW for northward oceanic transport) and Trenberth and Zhang (2019) (0.35 ± 0.02 PW for southward atmospheric transport and 0.22 ± 0.10 PW for northward oceanic transport), but they are very similar to those provided in Mayer et al. (2017). These values are listed in Table 4 for reference. Differences with earlier estimates are in part related to the updated, consistent treatment of water vapour enthalpy (Mayer et al. 2017) and can be understood from the following considerations: The hemispheric mass imbalance of the atmosphere arises from a net northward moisture flux across the equator of ~ 6 × 108 kg/s, which must be balanced by an oceanic return flow. If this mass flux is retained in the atmospheric transport calculations, we can estimate its contribution to the total atmospheric cross-equatorial energy transport as 1003 J kg−1 K−1 × 290 K × 6 × 108 kg s−1 ≈ 0.17PW (assuming a temperature of 290 K and using specific heat of dry air, which is inadequate but implicitly used widely in this type of computations), which closely matches the difference of earlier estimates with ours. Ideally, one would retain the enthalpy of moisture in the atmospheric computations and would also estimate the enthalpy carried by the cross-equatorial return flow in the ocean, the difference of which (essentially determined by the temperature differences) would be an unambiguous estimate of the northward energy transport accomplished by atmospheric moisture. This would be very small (~ 0.01PW assuming a \(\Delta \) T of 15 K) and hence neglect of enthalpy of moisture and effectively setting this transport contribution to zero is deemed much more adequate than the procedure in earlier works.

Table 4 Cross-equatorial atmospheric and oceanic energy transports (PW)
Full size table

The time series of global meridional transports at 30° N, equator and 30° S in ocean and atmosphere are displayed in Fig. 3. The mean oceanic poleward transport in Fig. 3a (solid black line) is calculated based on the surface fluxes and oceanic heat storage from five ORAS5 ensemble members. The shading denotes ± one standard deviation which increases with the integration distance from the pole. The transports at 30° N and the equator are inferred by the integration from the north pole, while the transport at 30° S is inferred by the integration from the south pole in order to reduce the errors. The contributions to the oceanic heat transport from surface flux (Fd) and oceanic heat storage are also plotted. The mean oceanic poleward transport at 30° N displays a significant decreasing trend (− 0.22 ± 0.08 PW decade−1) between 1995–2011. The poleward transport at 30° S displays larger interannual variability than at 30° N but with no obvious trend. The northward cross-equatorial oceanic transport is generally positive and has a similar trend as that at 30° N.

Fig. 3
figure 3

Time series of global meridional transports at 30° N, equator and 30° S in ocean (left column) and atmosphere (right column). Contributions of net surface energy flux and heat storage integrated from the north pole to oceanic transport are also plotted. Heat storage contribution and MEI lines are all adjusted up and down for clarity. Note the scale difference, and the three plots in the right panel have same vertical scale range

Full size image

The contributions from surface flux (Fd) and heat storage to ocean heat transport variability are also investigated (Fig. 3a). The integrated mean heat storage over 1985–2016 are 0.04, 0.11 and 0.18 PW at 30° N, equator and 30° S, respectively, so their variability time series are shifted in the vertical direction to match the mean transport to aid the comparison. It is found that the surface flux contribution determines the overall magnitude of the transport and the contribution from the heat storage integration determines the interannual variability. The correlation coefficients between the transport at 30° N, equator and 30° S and the integrated heat storage (90–30° N, 30° N-0, 90°–30° S) over 1985–2016 are all significant at the 95% confidence level and the values are 0.56, 0.89 and 0.64, respectively. The correlation coefficient between oceanic heat transport and MEI (Multivariate ENSO Index, (Wolter and Timlin 1998)) at the equator is 0.47 and significant, and the correlation coefficient between oceanic heat storage contribution and MEI is 0.42 and significant, implying that the oceanic heat storage contribution is partially modulated by ENSO variability, which may be related to the redistribution of OHC between the north and south tropical oceans during ENSO events (Mayer et al. 2014; Wu et al. 2018; Cheng et al. 2019). The factors affecting these variability merit further study.

The poleward atmospheric transports at 30° N, the equator and 30° S are shown in Fig. 3b–d. The trend of the atmospheric transports at 30° N is opposite in sign to the corresponding oceanic transports (r = − 0.69 and is significant at the 95% confidence level). Unlike the oceanic cross-equatorial transport, the atmospheric cross-equatorial transport displays an insignificant correlation with MEI index. The rapid decrease of cross-equatorial atmospheric transport from 1991–1992 is due to the Pinatubo eruption which reflects more solar radiation and reduces ASR preferentially in the northern hemisphere, decreasing the total atmospheric energy convergence in the northern hemisphere and the hemispheric atmospheric energy convergence difference, leading to decreased cross-equatorial atmospheric transport. However the reasons for the rapid decrease in 2001 and strong increase in 2011 remain unclear and will be further investigated in a future study.

3.3 Inferred Atlantic meridional energy transports

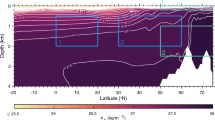
As an important component of the climate system, the Atlantic meridional heat transport is calculated using the method described in Sect. 2. The transport is integrated from the north pole and the results are plotted in Fig. 4a. The symbols represent observations from various sources and the bars are one standard deviation of multiple measurements. The observations are taken over different time periods and are not long term means so are plotted here for reference only. The inferred transports between 30° N and 80° N are higher than the observational means with a mean bias of 0.18 PW, which is within the mean uncertainty range. It should also be noted that the land correction may add uncertainty regionally and this could also contribute to the bias so should be further investigated in the future. The transports agree well with observations at locations south of 30° N.

Fig. 4
figure 4

a Multiannual mean (2006–2013) northward total meridional ocean heat transports (unit is PW) in Atlantic derived from the updated net DEEPC surface fluxes and observations (symbols, error bars show one standard deviation). The ocean heat storage derived from ORAS5 is also taken into account. The vertical dashed red line shows the location of 26° N. b Northward meridional ocean heat transports at 26° N of Atlantic from RAPID observations (red) and updated DEEPC net surface fluxes taking into account the sea ice melting and ocean heat storage of ORAS5 0–2000 m (solid black, grey shading is five member mean ± one standard deviation), together with the transports inferred from ERA-Interim model surface fluxes (dashed grey line) and the one derived using mass corrected atmospheric energy divergences (but no land surface flux adjustment) (solid light grey line). The multiannual mean (April 2004–March 2015) transports are also displayed in the plot

Full size image

In addition to short term observations in the Atlantic, the long term measurement at 26° N of North Atlantic is another very important indicator for derived net surface flux evaluation. The inferred time series of meridional energy transports at 26° N from different data sets are shown in Fig. 4b, together with the RAPID observations (Smeed et al. 2017). The time series of zonal mean heat storage in the Atlantic is derived from the adjusted 0–2000 m OHCT of ORAS5. The mean transports over April 2004–March 2015 are also displayed in the plot. The meridional oceanic heat transport inferred directly from the ERA-Interim reanalysis surface flux without applying mass correction (dashed grey line; mean of 0.66 PW) is unrealistically low. Applying a mass correction increases the mean transport over the RAPID data period to 1.00 PW. It was found by Liu et al. (2015) that the mass corrected atmospheric energy divergence/convergence still does not ensure the small global mean energy fluxes over land, so the excess/deficit energy over land was redistributed to the oceans (Liu et al. 2017) which also ensures physical consistency in the residual ocean heating based on the TOA energy imbalance. The inferred multiannual mean (April 2004–March 2015) transport from the updated net surface fluxes based on mass corrected atmospheric energy divergence/convergence and land surface flux adjustment (solid black line; mean transport of 1.23 PW) is very close to the RAPID observation of 1.22 PW, considering the observation uncertainty of ± 0.40 PW (Johns et al. 2011). The variability over 2008–2016 agrees well between the inferred estimates (solid black line) and RAPID (solid red line) (r = 0.66). The earlier trend of RAPID data from 2006–2009 is subject to greater uncertainty in observations (Trenberth et al. 2019; Trenberth and Fasullo 2018).

3.4 Atmospheric energy transport from ocean to land

The energy transport from ocean to land is determined by dry static energy (relating to temperature contrasts) and the transport of latent heat through moisture transport so is therefore closely related with the water cycle (Trenberth and Fasullo 2013). It also modulates the relative response of land and ocean to climate change with the land ocean warming contrast playing a central role in water cycle responses including extremes (Byrne and O’Gorman 2016). It is therefore important to quantify this transport and its variability. The ocean to land energy transport is inferred from the integration of atmospheric energy convergence over land area and the results are shown in Fig. 5. A radiative energy imbalance of 2.99 PW at the TOA is observed over the oceans for the 2006–2013 period. Less than 12% of this imbalance enters into the ocean while the remainder (about 2.65 PW) is primarily transported by the atmosphere over the land. This is slightly higher than the estimated 2.5 PW by Trenberth and Fasullo (2013) over 1979–2010, which is partly due to different assumptions of heat uptake by the land (if the land uptake is set to zero in our calculation, the transport will be about 2.61 PW) and partly due to different methods employed.

Fig. 5
figure 5

a Updated observations of energy flows between ocean and land regions in the climate system in petawatts (PW) over 2006–2013. TOA radiative flux is from CERES EBAF 4.1 anchored to 0.71 W m−2 (0.36 PW) over 2006–2013. b Time series of the transport from ocean to land, together with the MEI which is divided by 10 and shifted up to match the transport, and the TOA net flux over land multiplied by − 1. The 5 years mean transports are displayed at the top. c Scatter plot of global land precipitation and ocean to land energy transport. d Scatter plot of TOA net flux over land and ocean to land energy transport. Data points in the scatter plots are annual means and the correlation coefficients are also displayed

Full size image

The time series of the transport is shown in Fig. 5b and the 5 years mean transports are displayed at the top of the plot. The estimate of ocean to land energy transport for 2006–2013 is 0.14 PW lower than that in the earlier 1985–2004 period, and the reason is still under investigation. As the cross-equatorial oceanic transport is partially modulated by ENSO variation as discussed above (Fig. 3a), the variability of ocean to land energy transport is significantly positively correlated with MEI (r = 0.57). The time series of net TOA radiative flux over land is also plotted, and there is good agreement in the variability and trend between the transport and the net TOA flux over land (r = − 0.79, Fig. 5d) as expected due to small heat storage by the land and atmosphere. There is a negative relationship between the annual mean transport and the annual mean precipitation over land (Fig. 5c), since the ENSO events move the precipitation between land and oceans (Liu and Allan 2013) and alters sensible heat flows, but the correlation is not significant (r = − 0.30).

4 Conclusions

Study of energy flows in the Earth system is important for understanding climate change: the energy absorbed by the top layer ocean can determine the surface temperature variability while energy entering the deeper ocean can accumulate and affect long-term climate change (Otto et al. 2013; Richardson et al. 2016). Recognising these processes can help in explaining climate variability, including for example the slower than expected global surface warming at the beginning of the century (Easterling and Wehner 2009; Knight et al. 2009; Trenberth and Fasullo 2013; Su et al. 2018). It is therefore essential to accurately observe and understand changes in energy fluxes at the TOA and the surface. For this purpose, updated satellite observations and state of the art reanalysis products are combined with an improved methodology to provide new estimates of Earth’s top of atmosphere and surface energy fluxes, derived meridional and ocean to land heat transports and their variability since 1985. The motivation is to better quantify how energy is accumulating and being distributed across the globe, thereby advancing understanding of current climate change. The latest version of CERES Ed4.1 global mean net TOA radiation flux shows higher significant trend over the period 2001–2014 (0.34 ± 0.15 W m−2 decade−1) than in the previous version used (0.12 ± 0.13 W m−2 decade−1 in CERES Ed2.8) that is explained by reduced reflected shortwave radiation. The net TOA flux trends over 1985–2000 and 2001–2014 are qualitatively consistent with OHC changes (Cheng et al. 2017), with a slow increase of OHC in the first period followed by a fast increase over the second period.

Based on Mayer et al. (2017), the atmospheric energy convergences/divergences are re-calculated by considering both mass imbalance and consistent treatment of enthalpy of water substances using ERA-Interim output. The surface net energy flux is then estimated by combining the updated TOA flux and the new atmospheric energy transport. The land surface flux adjustment proposed by Liu et al. (2015, 2017) is applied and the mean net land surface flux is anchored to a new estimate of 0.2 W m−2 over 2004–2015 (Gentine et al. 2019) rather than 0.08 W m−2 over 1985–2012 in previous studies (Liu et al. 2015, 2017), although the impact of this adjustment on our results is small.

In the estimation of the surface heat flux entering the ocean, the sea ice melting and freezing are accounted for using five ORAS5 ensemble members. The meridional oceanic heat transport are calculated using the surface flux and oceanic heat storage estimated from ORAS5. The multiannual mean (2006–2013) northward meridional oceanic heat transport by the Atlantic is calculated and there is generally good agreement with observations (mean bias of 0.03 PW with a standard deviation of 0.19 PW). The time series of oceanic heat transport at 26° N of North Atlantic is inferred. The magnitude and variability between 2008 and 2016 agrees well with the RAPID observations (r = 0.66). The multiannual mean (April 2004–March 2015) transport (1.23 PW) is close to the RAPID observation of 1.22 PW and higher than that from estimated surface flux without land surface flux adjustment. This implies that the land surface flux adjustment is necessary but it is expected that this will not be required with further improvements in the calculation of energy transports, using higher time and space resolution data. Bryden et al. (2019) compared our ocean surface fluxes with that inferred from observed RAPID transport and measured OHCT, and it is found that our surface fluxes are smaller than theirs. Since the oceanic heat transports from two data sets are very close, this discrepancy is from their observed OHCT which has large uncertainty.

The oceanic and atmospheric transports at 30° N, the equator and 30° S are calculated. For oceanic heat transport, the contributions from surface flux and heat storage are estimated, and it is found that the surface flux contribution determines the magnitude of the transport, while the heat storage determines the interannual variability of the transport. The variability of the cross-equatorial oceanic heat transport and the oceanic heat storage contribution is partially modulated by ENSO due to the redistribution of OHC between northern and southern hemispheres during ENSO events (Wu et al. 2018; Cheng et al. 2019). The correlation coefficient between the cross-equatorial oceanic heat transport and MEI is 0.47 and significant at the confidence level of 95%, and the correlation coefficient of 0.42 between the oceanic heat storage contribution at the equator and MEI is also significant. The atmospheric energy transport at 30° N is significantly anti-correlated with the oceanic heat transport at the same latitude (r = − 0.54).

The multiannual mean cross equatorial atmospheric and oceanic transports are inferred by considering the multiannual mean ocean heat storage and zonal mean oceanic heat transport from five ORAS5 ensemble members. The inferred mean cross equatorial oceanic transport over 2006–2013 is estimated as 0.50 PW which is higher than those from previous studies (0.32 PW in Liu et al. (2017) and 0.45 PW in Stephens et al. (2016)) but in agreement with Mayer et al (2017), who applied a similar treatment of enthalpy energy of water substances in the atmosphere.

The inferred multiannual mean (2006–2013) atmospheric energy transport from ocean to land is about 2.65 PW, which is slightly higher than the 2.5 PW estimated by Trenberth and Fasullo (2013) and may be due to different land surface heat uptake assumptions and method employed. The variability of the ocean to land energy transport is partially modulated by ENSO (correlation with MEI is 0.55). The precipitation is also regulated by ENSO which moves the precipitation from land to oceans during El Nino events. However, this would imply weaker latent heat transport by moisture and so the observed increase in total energy transport during El Nino events is expected to be explained by increased sensible heat transport from ocean to land (or reduced sensible heat transport from land to ocean).

The results presented here are relevant for large scales, but it must be considered that contributions to the transport, including air-sea heat exchange (vertical heat flux), cross a broad range of scales. Large-scale air-sea heat exchange can be critically controlled by small-scale ocean eddy motions called submesoscales, which dominate the ocean vertical motions (and hence fluxes) (Torres et al 2018; Klein et al 2019; Yu et al 2019). In terms of the large discrepancies of the TOA radiative fluxes and surface fluxes between observations, reanalysis and model simulations, the diagnostic tool of Lembo et al. (2019b) may be employed to compare the results, and more in-depth studies are needed using the latest available data sets including the fifth-generation ECMWF reanalysis (ERA5). In this study, only ORAS5 data are employed for the calculation of ocean heat content and its change, so future work should incorporate more observation-based ocean analyses. Interpretation of the physical processes governing variability in Earth’s energy flows that are presented in this work will contribute to advancing understanding the current trajectory of climate change.