Abstract
We examine whether significant changes in ocean temperatures can be detected in recent decades and if so whether they can be attributed to anthropogenic or natural factors. We compare ocean temperature changes for 1960–2005 in four observational datasets and in historical simulations by atmosphere-ocean general circulation models (AOGCMs) from the Coupled Model Intercomparison Project phase 5 (CMIP5). Observations and CMIP5 models show that the upper 2000 m has warmed with a signal that has a well-defined geographical pattern that gradually propagates to deeper layers over time. Greenhouse gas forcing has contributed most to increasing the temperature of the ocean, a warming which has been offset by other anthropogenic forcing (mainly aerosols), and volcanic eruptions which cause episodic cooling. By characterizing the ocean temperature change response to these forcings we construct multi-model mean fingerprints of time-depth changes in temperature and carry out two detection and attribution analysis. We consider first a two-signal separation into anthropogenic and natural forcings. Then, for the first time, we consider a three signal separation into greenhouse gas, anthropogenic aerosols and natural forcings. We show that all three signals are simultaneously detectable. Using multiple depth levels decreases the uncertainty of the results. Limiting the observations and model fields to locations where there are observations increases the detectability of the signal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Observational estimates show that approximately 93\(\%\) of the energy entering the climate system since the 1950s has gone into the oceans (e.g. Levitus et al. 2000, 2005, 2012; Ishii and Kimoto 2009; Lyman et al. 2010; Trenberth 2010). As a result the ocean heat content (OHC) has increased with a characteristic spatiotemporal distribution. Many studies have estimated the variability of OHC from subsurface ocean temperature observations (e.g. Levitus et al. 2000, 2005, 2012; Willis et al. 2004; Ishii and Kimoto 2009; Gouretski and Koltermann 2007; Palmer et al. 2007; Palmer and Haines 2009; Palmer and Brohan 2011; Domingues et al. 2008; Roemmich et al. 2012; Balmaseda et al. 2013; Lyman and Johnson 2014; Roemmich et al. 2015; Cheng et al. 2016) and shown qualitatively similar global OHC time-series from 1955 to recent years. OHC is characterised by an overall warming trend, with superimposed variability and some cooling events attributed to major volcanic eruptions (Agung in 1963, El Chichón in 1982 and Pinatubo in 1991) and El Niño Southern Oscillation (ENSO) variability (e.g. 1998). Spatially integrated OHC timeseries over different depths show that most of the ocean heat uptake (OHU, defined as the ocean heat content increase) has occurred in the upper layers of the ocean (e.g. Levitus et al. 2000, 2005, 2012; Balmaseda et al. 2013).
Detection and attribution studies have shown that the observed changes in ocean heat content (OHC) are consistent with simulations of atmosphere ocean general circulation models (AOGCMs) forced with historical increases in greenhouse gases, anthropogenic aerosols and solar and volcanic forcings (e.g. Levitus et al. 2001; Hansen et al. 2002; Sun and Hansen 2003; Gent and Danabasoglu 2004; Gregory et al. 2004; Sedláček and Knutti 2012; Cheng et al. 2016; Gleckler et al. 2016). The OHC response to greenhouse gases is partly offset by anthropogenic aerosols and volcanic aerosols, and is inconsistent with unforced variability. The forced pattern of warming relates well to the observed pattern. It shows a smooth gradual propagation of the surface signal to the intermediate depths, and can be explained in terms of advection and diffusion processes which transport heat from the surface to deeper layers (e.g. Sedláček and Knutti 2012; Llovel et al. 2013). Gleckler et al. (2016) analysed a set of CMIP5 models and their results suggest that nearly half of the increase in global OHC with respect to pre-industrial has occurred in recent decades with over a third of the accumulated heat occurring below 700m.
Other studies have used a more rigorous statistical approach to arrive at similar conclusions (e.g. Barnett et al. 2001, 2005; Reichert et al. 2002; Pierce et al. 2006, 2012; Palmer et al. 2009; Gleckler et al. 2012; Weller et al. 2016). Barnett et al. (2001) pioneered ocean temperature detection and attribution studies by showing that OHC estimated in the Levitus et al. (2000) dataset agrees with historical simulations from a climate models only when the anthropogenic forcing is included. Of particular relevance to the present work, citetbarnett05warming and Pierce et al. (2006) showed by considering spatial-only and space-time fingerprints of individual depth levels, that a warming in the upper layers of the ocean (down to 300m) can be detected (even in individual basins), and that this is consistent only with anthropogenic forcing and cannot be explained by natural forcings or unforced variability. With the ongoing improvements of observational datasets (new data and new instrumental bias corrections) and climate models (CMIP3 and CMIP5), Gleckler et al. (2012) and Pierce et al. (2012) use higher temporal resolution and a multi-model framework (earlier studies used few models) to reiterate earlier conclusions and show that the anthropogenic signal is detected even more robustly.
Consistent with these results, but using a different statistical method (optimal fingerprinting, the method used in this paper), Reichert et al. (2002) detected the anthropogenic fingerprint in temperature change integrated over the upper 300 m and 3000 m. More recently Palmer et al. (2009) showed, using optimal fingerprinting, that considering the temperature change above the 14 °C isotherm maximises the detectability of the anthropogenic signal, since most of the heat of anthropogenic origin is found in the upper layers, by filtering out some of the dynamic ocean variability that may obscure the climate change signal. Weller et al. (2016) built upon this work using CMIP5 models in a multi-model framework, finding that both anthropogenic and natural forcing influences are detected in upper ocean temperature change in the global mean and in individual ocean basins.
In this paper carry out a detection and attribution analysis examining whether ocean temperature change for 1960–2005 is attributable to anthropogenic and natural forcings, using CMIP5 climate model simulations (Taylor et al. 2012) and four observational datasets (Sect. 2). First we compare ocean temperature in four observational products and CMIP5 model simulations of recent decades (1960–2005) to evaluate the models, characterize the temperature change patterns and inform the construction of fingerprints (Sect. 3). Next we investigate the sensitivity of the datasets to the temporal and geographical sparseness of observations by masking observations and models (Sect. 4). Finally we carry out a multi-model detection and attribution analyses, using optimal fingerprinting, based on the time and depth structure of the temperature together, which allows a clearer separation of signals than in previous studies (Sect. 5). We carry a two-signal analysis separating anthropogenic (ANT) and natural (NAT) signals and a three-signal analysis considering greenhouse gas (GHG), other anthropogenic (OA) and natural (NAT) signals. The two-signal analysis allows for comparison with previous work (e.g. Barnett et al. 2005; Gleckler et al. 2012; Pierce et al. 2012; Weller et al. 2016) and shows the value of including vertical structure of the temperature change. The three-signal combination has not been attempted before for ocean temperature change.
2 Ocean temperature observations and CMIP5 AOGCMs
For the analysis of climate variables from a detection and attribution perspective it would be ideal to have measurements covering extensive spatial and temporal scales to allow determining changes accurately over time. While there have been significant developments in the quantity and quality of ocean temperature measurements, the spatial coverage is insufficient to make estimates of globally integrated ocean heat content change before the 1960s (e.g. Lyman and Johnson 2008; Abraham et al. 2013). The observational datasets used in this paper are Ishii and Kimoto (2009) (referred to as IK09 hereafter), Levitus et al. (2012) (referred to as Lev12 hereafter), Met Office Hadley Centre ‘EN’ version 4.1.1 (Good et al. 2013) with two different XBT corrections (Levitus et al. 2009; Gouretski and Reseghetti 2010) (referred to as \(\hbox {EN4}_{{Lev}}\) and \(\hbox {EN4}_{{GR10}}\) hereafter) and European Centre for Medium-range Weather Forecasts (ECMWF) Ocean ReAnalysis System 4 (ORAS4) (Balmaseda et al. 2012). ORAS4 differs from the other datasets as it is a reanalysis, produced by combining via data assimilation methods the output of an ocean model forced by atmospheric reanalysis fluxes with quality controlled ocean observations, relaxed to SST and bias corrected (Mogensen et al. 2012). The other three observational datasets use different statistical infilling methods to combine the available observations into spatially complete gridded fields; these methods require estimating the ocean temperature climatology. Four observational datasets are considered since the differences between them (arising from their different selections of observations, quality control methods, infilling methods and instrumental bias corrections) will provide an indication of the observational uncertainty.
In this paper we use various model simulations from CMIP5, which provides a protocol for a large range of climate simulations that allow investigating climate variations and the effect of external forcings on the climate system (Taylor et al. 2012). In the control simulation, constant pre-industrial atmospheric concentrations (year 1850) of all well-mixed gases (including some short-lived), natural aerosols (either by emissions or concentrations) and land use are prescribed. These experiments are used to characterise unforced climate variability. In the historical experiment, all of these vary as they did in reality from the mid-nineteenth century to 2005. In order to attribute the observed climate changes to particular causes (i.e. external forcings), simulations of the historical period are carried out with only a subset of the forcings.
HistoricalGHG simulations have the observed variation in well-mixed greenhouse gases only. HistoricalNat has natural forcings only, that is, volcanic aerosols and variations in solar output. Since few models provided simulations with anthropogenic aerosols only (historicalAA), this signal is difficult to distinguish. Therefore instead the historicalOA signal has been estimated, where OA refers to ‘other anthropogenic’, by subtracting the response of the historicalNat and historicalGHG simulations from the historical ‘all forcings’ simulation. This includes the response to anthropogenic aerosols, ozone and land use change, among which the first aerosol forcing is dominant, so historicalOA should be very similar to historicalAA. Note that the historicalOA is only estimated for the multi-model means as the number of ensemble members for individual models is not sufficient to remove the effects of unforced internal variability. We have not attempted to determine the OHU response to ozone and land use change, for which the CMIP5 dataset is not adequate (not enough models, or the experiments do not allow them to be distinguished). Furthermore, note that in all these simulations, the temperature change fields have been corrected for “control drift” (see Appendix 1), and the historical and historicalNat simulations have been corrected for “volcanic drift” too (see Appendix 2).
Some modelling institutions provide for each experiment an ensemble of up to 10 simulations, which are initialised from different conditions and diverge due to the chaotic nature of the climate system, producing different unforced variability (with the same statistical properties). Having a large ensemble of simulations is helpful since ensemble averaging will reduce unforced climate variability that may mask forced responses. The mean of an infinitely large ensemble would show only the response to external forcings, but we do not expect the ensemble mean to reproduce the observations exactly since the observations are only a single realisation with its own unforced variability. To minimise the unforced variability contaminating the expected signal, we use the CMIP5 multi-model ensemble mean, giving equal weights to all the models. Therefore if an ensemble of simulations is available for a particular model, we take the ensemble mean first, and then calculate the multi-model mean. Detection and attribution studies have shown improved results using the multi-model mean (e.g. Gillett et al. 2002; Jones et al. 2013; Weller et al. 2016). This is partly because the multi-model mean resembles observations more closely than any individual model does, due to cancellation of model errors as if they were random (Reichler and Kim 2008). This assumption requires that models are statistically independent from each other. Actually they are not due to the exchange of ideas and code between modelling groups, which may result in common response patterns and biases among models Knutti et al. (2013). Hence there are limitations to the statistical interpretation of the ensemble spread (e.g. Tebaldi and Knutti 2007; Knutti 2010; Pennell and Reichler 2011; Storch and Zwiers 2012).
3 Comparison of annual mean ocean temperature change in observations and CMIP5 AOGCMs
This section compares simulated ocean potential temperature change in CMIP5 historical simulations with observations from 1960 to 2005. Several diagnostics are used in this analysis (time-series, temperature change vertical profiles, temperature change as a function of time and depth and geographical distribution of ocean heat content change) with the objective of characterising spatial and temporal structure of the warming and informing the construction of fingerprints for the detection and attribution study.
3.1 Temperature change as a function of time and depth
We calculate global mean temperature change profiles in K (from the surface to 2000 m depth) for the 45 year period of 1960 to 2005 (CMIP5 historical simulations end in this year) from the observational products and the model mean of CMIP5 historical simulations (Fig. 1) by multiplying the linear least-squares temporal trend (K/yr) of global mean temperature by 45 years. Observations and models show that the ocean has warmed throughout most of the water column and the warming is greatest at the surface (Fig. 1). In EN4GR10 and ORAS4 between 150 and 200 m there has been no net warming (Fig. 1a), this is caused by cooling in parts of the tropical Pacific and Indian oceans at these depths, which compensates the warming that occurs elsewhere in the global mean. This feature is not evident in Lev12 and IK09, nor in the CMIP5 model mean.
a Global mean temperature change [K] profiles of different observational products and CMIP5 model mean for the period between 1960–2005. b Global mean temperature change [K] profiles of historical simulations for individual CMIP5 AOGCMs for the period 1960–2005, the thicker line is the CMIP5 model-mean. In both figures the profiles were calculated from temporal linear trends. The dotted lines in both plots shows the 5th and 95th percentiles from the distribution of equal length trends calculated from CMIP5 pre-industrial control simulations. The dashed line indicates the origin
Temperature change [K] profiles of CMIP5 simulations for the period between 1960 and 2005 for a historicalNat, b historicalGHG and c historicalAA simulations. The dotted lines in all plots shows the 5th and 95th percentiles from the distribution of equal length trends calculated from CMIP5 pre-industrial control simulations. The black dashed line in figure c is the historicalOA, calculated by subtracting the model means of the historicalNat and historicalGHG from the historical simulations
The historical CMIP5 multi-model profile is qualitatively similar to the observations, but with less surface intensification and a more gradual decrease in warming with depth. Figure 2 suggests that natural forcings (solar and volcanic) have contributed little to OHU (except in GFDL-ESM2M) (Fig. 2a), while greenhouse-gas forcing has contributed most (Fig. 2b) partially offset by anthropogenic aerosol forcing (Fig. 2c). Note that anthropogenic aerosol is the dominant global forcing in historicalOA, as shown by similarity of the black solid (estimated from historicalAA) and dashed lines (estimated from historicalOA) (Fig. 2c).
Figure 1b shows that the spread among the CMIP5 AOGCMs is greater than among observational products, and observations lie within the model spread. Six of the models (ACCESS1-0, ACCESS1-3, CSIRO-Mk3-6-0, GFDL-CM3, HadGEM2-ES, HadGEM2-CC) show subsurface cooling (Fig. 1b), not consistent with any of the observational products. This could be that the anthropogenic aerosol forcing is too strong or the response to aerosols in those models is overestimated (Fig. 2c). Consistent with this hypothesis, CSIRO-Mk3-6-0 and GFDL-CM3 show a greater cooling in the historicalAA experiments, compared to IPSL-CM5A-LR and NorESM1-M. However few CMIP5 models provided historicalAA simulations so this inference is tentative. Conversely, the rest of the models tend to overestimate the rate of warming.
According to the simple model of Gregory and Forster (2008), the profile differences could be explained by differences in forcings (F) used in the models, or in model responses to the forcings. Following Kuhlbrodt and Gregory (2012), we distinguish these possibilities by dividing each profile by its vertical integral (Fig. 3), omitting models which have a negative integral. After scaling, the shape of the temperature change profiles is solely related to efficiency of the processes of vertical heat transport of ocean heat uptake. As in the CMIP3 model analysis by Kuhlbrodt and Gregory (2012), the warming in CMIP5 models is less surface-intensified than in observations (Fig. 3a).
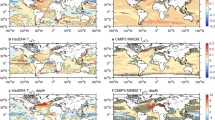
OHC [\(10^{9}\, {\text{J}}{\text{m}}^{-2}\)] change integrated over the upper 2000m for 1960–2005 for a ORAS4, b\(\hbox {EN4}_{{GR10}}\), c\(\hbox {EN4}_{{Lev}}\), d Lev12, e IK09 and f CMIP5 model mean. g and h Show the standard deviation of the observational products and CMIP5 models respectively. The color bar on the left is for figures a–f, and the color bar on the right is for g–h
Comparing the 5th and 95th percentiles of the 45 year trends simulated in CMIP5 pre-industrial control simulations (which have no external forcing) with observed and simulated historical profiles (dotted lines in Figs. 1 and 2) indicates that that the warming is inconsistent with simulated unforced internal variability at all depths in most cases (with 90\(\%\) confidence). Similarly, the warming due to GHG (Fig. 2b) and the cooling due to anthropogenic aerosols (Fig. 2c) are significant, but the temperature change in response to natural forcings is not (except in GFDL-ESM2M).
The rate of warming is not constant in time. Observations and CMIP5 models show that the warming signal propagates from the surface to the deeper layers with inter-annual variations (Fig. 4) (e.g. Cheng et al. 2016; Gleckler et al. 2016). Observational products have a similar increasing trend over this period but obvious differences in interannual and decadal variability, explained by the different ocean datasets, data quality control, bias corrections and infilling methods used to complete the data. Llovel et al. (2013) found statistically significant lag correlations between the upper (0–300 m) and lower (300–700 m) layers for time lags between − 9 and 24 years in observations, not being able to estimate a unique time-scale due to uncertainties and the short length of the record.
Global mean temperature change [K] profiles for the period between 1960 and 2005 for full (black) and sub-sampled (red) fields for a ORAS4, b EN4GR, c EN4L, d CMIP5 model-mean. In all figures the profiles were calculated from temporal linear trends and the change is for the entire time period. The dashed line indicates the origin
Figure 5 shows the time-depth temperature change characteristic of particular forcings. The volcanic cooling signal caused by the three major volcanic eruptions (Agung, El Chichón and Pinatubo, Fig. 5a) propagates from the surface down to approximately 500 m. The increasing trend in historical simulations of CMIP5 models, for all depths, is caused by GHG characterised by a warming signal that propagates steadily from the surface to deeper layers and is surface intensified (cf. temperature change profiles, Fig. 2). On the other hand, anthropogenic aerosols (Fig. 5b–d) have partially offset GHG with a similar characteristic signal of opposite and weaker magnitude.
3.2 Geographical distribution of ocean heat content change
The geographical distribution of ocean heat content change in observations and models is not uniform (Fig. 6) because of the patterns of change in the atmosphere-ocean heat and windstress fluxes, ocean dynamics and their interactions. The Atlantic basin (except for the northern subpolar gyre) shows the strongest widespread warming. The Pacific ocean has also warmed but there are two (or three in the case of ORAS4) areas which have cooled located in the North Pacific and tropical western basin extending southward. The Indian Ocean shows cooling extending from the Indonesian through-flow and warming in the north. The Southern Ocean is characterised by a band of increased ocean heat uptake which is maximum at about 45\(^{\circ }\)S (Fig. 6). Overall, the Atlantic and Southern Ocean heat penetrates to deeper layers in comparison to the Pacific and Indian Oceans where the heat is more surface intensified.
ANT (blue) and NAT (green) signals scaling factors and uncertainty ranges for global mean ocean temperature change between 1960–2005 for one-layer integrated form the surface to different depths. Each column is for a different observational dataset. The top row are the results for spatially complete fields and the bottom row are for sub-sampled. The solid error bars show the 5–95\(\%\) uncertainty ranges. The dotted error bars are the results after scaling the noise estimates by the F-ratio (see Sect. 5.4.3). The tick (pass) or cross (fail) on the left of each D&A experiment indicates whether the residual consistency test passes before scaling by the F-ratio. These optimal detection results are using all the control EOFs, that is, not truncated
The geographical pattern of ocean heat content shows qualitative similarities in the large scale ocean features among observations (Fig. 6a–e), but there are regional differences due to the infilling method and quality control used in each product, with ORAS4 being the most distinct compared to the products. The spread among the observational products (Fig. 6g) shows that the largest spread occurs in the western boundary currents and Southern Ocean, which are the regions with the highest eddy kinetic energy (Palmer et al. 2015, 2017). The differences among the observed patterns increase with depth (not shown), indicating that ocean heat content change is better constrained at the surface.
The evident geographical pattern of the CMIP5 mean must be dominated by the influence of external forcings (Fig. 6f), because unforced variability is uncorrelated among model simulations, and will therefore be averaged out. Again, the largest spread is in the western boundary currents and the Southern Ocean, but models show significantly larger spread (Fig. 6h) than observations. For example, while all models show increased ocean heat content in the Southern Ocean, its location, shape and magnitude are model-dependent (Fig. 6h).
ANT (blue) and NAT (green) signals scaling factors and uncertainty ranges for global mean ocean temperature change between 1960–2005 for multiple depth level fingerprints. Each column is for a different observational dataset. The top row are the results for spatially complete fields and the bottom row are for sub-sampled. The solid error bars show the 5–95\(\%\) uncertainty ranges. The dotted error bars are the results after scaling the noise estimates by the F-ratio (see Sect. 5.4.3). The tick (pass) or cross (fail) on the left of each D&A experiment indicates whether the residual consistency test passes before scaling by the F-ratio. These optimal detection results are using all the control EOFs, that is, not truncated
ANT (blue) and NAT (green) signals scaling factors and uncertainty ranges for ocean temperature change for multiple regions between 1960 and 2005 for a one-depth layer fingerprint: 0-300m. Each column is for a different observational dataset. The top row are the results for spatially complete fields and the bottom row are for sub-sampled. The solid error bars show the 5–95\(\%\) uncertainty ranges. The dotted error bars are the results after scaling the noise estimates by the F-ratio (see Sect. 5.4.3). The tick (pass) or cross (fail) on the left of each D&A experiment indicates whether the residual consistency test passes before scaling by the F-ratio. These optimal detection results are using all the control EOFs, that is, not truncated
GHG (blue), NAT (green) and OA (red) signals scaling factors and uncertainty ranges for global mean ocean temperature change between 1960 and 2005 with multiple depth layer fingerprints. Each column is for a different observational dataset. The top row are the results for spatially complete fields and the bottom row are for sub-sampled. The solid error bars show the 5–95\(\%\) uncertainty ranges. The dotted error bars are the results after scaling the noise estimates by the F-ratio (see Sect. 5.4.3). The tick (pass) or cross (fail) on the left of each D&A experiment indicates whether the residual consistency test passes before scaling by the F-ratio. These optimal detection results are using all the control EOFs, that is, not truncated
Any similarity between observations and the CMIP5 model mean would suggest that the observed pattern of ocean heat content change could be attributed to external climate forcings. This applies to the greater warming in the Atlantic basin and the Southern Ocean evident in observations and historicalGHG (Figs. 6, 7b). The Southern Ocean has a band of increased ocean heat uptake centred at about 45\(^{\circ }\)S, due to increased surface heat input and enhanced Ekman pumping, caused by GHG forcing perhaps and stratospheric ozone depletion (Fig. 7b) (e.g. Cai 2006; Fyfe et al. 2007; Bouttes et al. 2012; Ferreira et al. 2015; Armour et al. 2016). Other anthropogenic forcings (Fig. 7c, d) cool the ocean with a similar pattern to GHG but of opposite magnitude, despite the possible geographical differences in the forcings (e.g. Myhre et al. 2013). Natural forcings (solar and volcanic) simulations show only a weak pattern of OHC change (Fig. 7a) in most of the world. All simulations show a dipole pattern in the North Atlantic, which could be associated with changes in the Atlantic meridional overturning circulation, but its pattern is different in response to anthropogenic and natural forcings, and both are different from observations.
4 Sub-sampling ocean temperature change observations and CMIP5 AOGCMs
Climate models datasets are often sub-sampled for comparison with observational products in order to replicate the observational coverage and thus avoid additional assumptions associated with the observational infilling procedure (e.g. Hegerl et al. 2001; Barnett et al. 2001, 2005; Reichert et al. 2002; Pierce et al. 2006, 2012; Palmer et al. 2009; Gleckler et al. 2012). The effect of the infilling method can be studied by comparing subsampled model datasets with the “full fields” i.e. complete datasets (e.g. Gregory et al. 2004; Pierce et al. 2006; AchutaRao et al. 2006, 2007; Palmer et al. 2007; Palmer and Haines 2009; Gleckler et al. 2012; Lyman and Johnson 2014; Good 2016; Boyer et al. 2016). To do this we derive the observational “mask” (which distinguishes gridboxes that are included in and those that are excluded from observational coverage) of the EN4 dataset (Good et al. 2013), by the method described in Appendix 3, and apply it to the observational products and CMIP5 models.
Joint distributions of the estimated signals: GHG vs. OA (red), GHG vs. NAT (blue) and NAT vs. OA (green) GHG for global mean ocean temperature change between 1960–2005 for multi-level fingerprints 3 layers (0–300 m, 300–700 m and 700–2000 m) and sub-sampled fields, for a ORAS4, b EN4GR10, c EN4Lev and d IK09. The area enclosed contains 90\(\%\) of the estimated joint distribution amplitudes
GHG (blue), NAT (green) and OA (red) signals scaling factors and uncertainty ranges for ocean temperature change constructed from four regions (Atlantic, Pacific, Indian and Southern Oceans) between 1960–2005 for multiple depth level fingerprints. Each column is for a different observational dataset. The top row are the results for spatially complete fields and the bottom row are for sub-sampled. The solid error bars show the 5–95\(\%\) uncertainty ranges. The dotted error bars are the results after scaling the noise estimates by the F-ratio (see Sect. 5.4.3). The tick (pass) or cross (fail) on the left of each D&A experiment indicates whether the residual consistency test passes before scaling by the F-ratio. These optimal detection results are using all the control EOFs, that is, not truncated
For both the global mean and individual ocean basins, temperature change profiles of sub-sampled fields for observations and models show overall the same vertical structure as the infilled fields, but the magnitude of the changes are greater at all depths considered (down to 2000 m, Fig. 8). Sub-sampling the observational products and the CMIP5 model mean increases the warming at the surface. The subsurface cooling in observations, peaking at about 150 m of depth, becomes more pronounced.
Gleckler et al. (2012) suggest, based on the Lev12 and IK09 datasets, the explanation that the infilling method introduces a bias towards small magnitudes in data sparse regions. However, ORAS4 shows the same effect, despite its completely different derivation, maybe because the ocean model underestimates ocean temperature variability. Another possibility, which could explain the effect on all observational products, is that the observational coverage is biased to regions that have larger temperature changes (warming at most depths). This last explanation is the only possibility for CMIP5 models’ exhibiting the same behaviour (greater trends in sub-sampled fields, with no infilling methods). Biased spatial sampling seems therefore most likely to us, perhaps because the Atlantic, which is best observed, also tends to warm more.
Interannual and decadal temperature change variability is greater in the sub-sampled fields than in the infilled fields (Fig. 9) (cf. Gregory et al. 2004; AchutaRao et al. 2006, 2007; Barnett et al. 2005; Pierce et al. 2006; Gleckler et al. 2012). This is particularly evident at times and locations when the observations are sparsest, that is earlier in the record and at depth (below 300 m). This is probably because compensating anomalies, caused by rearrangement of ocean heat content or shifts in patterns of surface heat flux, may produce cancelling positive and negative anomalies in ocean temperature that will not cancel if not sampled fully.
Control drift in global mean ocean temperature change [K] averaged over the upper 2000m in CMIP5 pre-industrial control simulations. a Pre-industrial control run, b subtracting a linear fit and c subtracting a 4th order polynomial fit. The purpose of this figure is to show the drift in each of the models and therefore the starting point of each model is arbitrary. The vertical scale is shown by the error bar
a Global mean temperature change timeseries averaged over the upper 2000 m for 1860–2005 of hitoricalNat simulations (pre-industrial control corrected) of CMIP5 models. b Model mean timeseries with the temporal linear trend subtracted. In a the thick lines are the ensemble mean of each model individually, which are de-trended in (b). The purpose of the plot is to illustrate the volcanic drift in each CMIP5 model and therefore the starting point in the y-axis is arbitrary. The vertical scale is shown by the error bar
The agreement among observational datasets in respect of interannual and decadal variability is better in sub-sampled than infilled fields. This implies that the infilling procedure introduces systematic uncertainty. On the other hand, since it may also introduce biases, both spatially complete and sub-sampled fields are used in detection and attribution studies.
5 Detection and attribution of ocean temperature by optimal fingerprinting
Optimal fingerprinting is a technique based on multiple linear regression (e.g. Hasselmann 1979, 1993, 1997; Hegerl and von Storch 1996; Hegerl et al. 1997; Allen and Tett 1999; Thorne 2001; Stott et al. 2001, 2003; Tett et al. 2002; Allen and Stott 2003; Allen et al. 2006). In Sect. 5.1 we summarise the method, and in Sect. 5.2 the construction of fingerprints. Section 5.3 presents analyses for two signals (ANT and NAT) and Sect. 5.4 for three (GHG, NAT and OA).
5.1 Methodology
Optimal fingerprinting assumes that observations y may be represented as a linear sum of simulated signals (\(X_i\), referred to as fingerprints) in response to external forcings to the climate system, and unforced internally generated variability (\(\varepsilon\), also referred to as climate noise),
where \(\beta _i\) are scaling factors (also referred as amplitudes) corresponding to each of the fingerprints and n refers to the number of fingerprints.
The observations and fingerprints can have spatial and/or temporal dimensions e.g. a geographical pattern of change or time-series for multiple layers. The method assumes that the spatiotemporal responses X are correctly simulated regarding patterns, but not necessarily regarding amplitudes, and the beta are chosen to give the best fit to the observations. Thus, the method may indicate deficiencies in the magnitudes of response.
We assume that the fingerprints are perfectly known (have no errors) and therefore have no uncertainty; this is an acceptable approximation if we compute the fingerprints from a large ensemble of runs. In that case, the optimal \(\beta\) are evaluated using ordinary least squares (OLS) regression (Allen and Tett 1999),
where \({\tilde{\beta }}\) refers to the best estimate of \(\beta\) and \(C_{N}\) is the covariance of unforced variability, whose effect is to give higher weight to aspects of the response with greater signal-to-noise ratio and thus maximise the statistical significance. In the optimal fingerprinting algorithm, weighting by the inverse noise covariance is actually carried out by projecting the observations y and fingerprints X onto the EOFs scaled by the inverse singular values of \(C_{N}\), then the scaling factors are calculated using the OLS regression in the rotated space, so as to give more weight to those regions of phase space with lower unforced variability and less weight to those regions of phase space with higher unforced variability. This method thus allows to consider a truncated representation by projecting onto n leading EOFs, reducing the dimensions of the observations and fingerprints to the number of highest rank EOFs given by n, which has potential implications on the outcome. The maximum number of EOFs (maximum truncation) that can be estimated from the control depends on the size of the fingerprints and the length of the control simulation, which might not allow to estimate all EOFs.
In this study the size of the fingerprints (due to sufficient temporal and spatial averaging) and the amount of years of control available allow estimating all EOFs (i.e not truncating). Nevertheless, many studies have investigated the sensitivity of the results to truncation and we refer the reader to those (Hegerl and von Storch 1996; Allen and Tett 1999; Stott et al. 2001; Tett et al. 2002; Allen and Stott 2003; Jones et al. 2013).
Since the observations y contain unforced variability, there is a statistical uncertainty in \({\tilde{\beta }}\), which is normally distributed with mean \(\beta\) and variance,
where \(C_{N_{2}}\) is another estimate of the noise covariance matrix, made independently of \(C_{N}\) (Allen and Tett 1999; Allen and Stott 2003). It is important to use independent estimates of noise covariance for the optimization and for the evaluation of uncertainty in order to avoid a systematic bias towards underestimation of the latter (Hegerl and von Storch 1996; Allen and Tett 1999).
It is not possible adequately to evaluate unforced variability from observations since they contain forced responses, do not cover the entire ocean and are at most 50 years long; which is insufficient to characterize variability on decadal or centennial time-scales. Therefore pre-industrial control run simulations AOGCMs are used, assuming that simulated variability gives a realistic estimate. \(C_{N}\) and \(C_{N_{2}}\) are estimated from independent sections of equal length from the control run.
Once we have estimated the scaling factors \({\tilde{\beta }}\) with their respective confidence intervals calculated from \(V({\tilde{\beta }})\), two tests are carried out to determine whether the signals are detected and their amplitude are consistent:
-
Detection: tests the null hypothesis that the observed pattern of response to a particular forcing or combination of forcings is consistent with zero and \({\tilde{\beta }}\) is positive. By consistent we mean the uncertainty of \({\tilde{\beta }}\) spans zero. If the uncertainty of \({\tilde{\beta }}\) is inconsistent with zero and positive, the null hypothesis is rejected and we conclude that the pattern is detected. Alternatively, if the uncertainty of \({\tilde{\beta }}\) is consistent with zero the null hypothesis is not rejected and we conclude that the pattern is not detected.
-
Amplitude consistency: assuming that the signals are detected, we next test the null hypothesis that the amplitude of the observed response is consistent with the simulated response. If the uncertainty range of \({\tilde{\beta }}\) includes unity then the simulated pattern/s is/are consistent with observations. If the uncertainty of the \({\tilde{\beta }}\) does not span unity the null hypothesis is rejected: if below unity, the simulated pattern of response is overestimated and therefore scaled down; if above unity, the simulated pattern of response is underestimated and therefore scaled up.
5.2 Constructing the fingerprints
To construct the CMIP5 multi-model mean fingerprints we use only those 8 models for which historical, historicalNat and historicalGHG simulations are all available are used, resulting in 40, 24 and 26 model simulations respectively (see Table 1). All the fingerprints are for the 46 years 1960–2005.
The simplest fingerprint we consider is a timeseries for the global mean or a specific geographical region (ocean basin or latitude/longitude range) and one layer covering a particular depth range (e.g. 0–300 m). These fingerprints \(F_{N}(t)\) have only the time dimension, where the subscript N refers to a particular signal and t is the year The values are calculated from 3D annual means of ocean temperature by spatial averaging over the region of interest, weighted by the area of each grid cell, and then averaging the depth levels, weighted by the thickness of the levels.
The novelty in this study is to construct fingerprints with multiple levels which may allow us to discriminate the signals better by considering their vertical structure. These multi-level fingerprints \(F_{N}(t,l)\) have a dimension l for layer number (e.g. for two layers, 0–300 m and 300–700 m). The observations and each of the CMIP5 models have different numbers and depth of levels, so we calculated the vertical means by selecting the nearest available levels. Vertical interpolation was tested as an alternative but the differences in the results are negligible.
We also construct fingerprints considering multiple geographical regions: \(F_{N}(t,l,r)\), where r is the region number. This is particularly relevant for GHG and OA, which could be better discriminated since the anthropogenic aerosols are not well mixed and are concentrated in the Northern Hemisphere where they are mainly emitted.
For the optimal fingerprinting algorithm, the fingerprints are reshaped as X(N, j), where N is the number of fingerprints (one for each forcing or signal) and j is the number of elements in each fingerprint. Similarly, the observations have the form y(j). For example, with 46 years and two layers, \(j=2 \times 46 = 92\). If there are two regions and three layers \(j=2 \times 3 \times 46 = 276\).
5.3 Estimating unforced variability
A total of 5423 years are available from the pre-industrial control simulations of 8 CMIP5 models. Since their lengths are different, considering the entire control runs would bias the control covariance matrix to those models with longer control runs. To avoid this we follow previous studies (e.g. Gillett et al. 2002; Jones et al. 2013) by limiting the length of all control runs to the shortest available. With 500 years of each model 4000 years of control are used in total. Since two independent estimates of control are needed (for optimization and for the hypothesis testing), for each estimate 250 years of each control is used, concatenated to make a sequence of 2000 years. Segments are extracted from this sequence with dimension C(t, l, s), where t is year number within the segment, l is the number of levels and s is the number of segments. To maximise the amount of information that is used in calculating the noise covariance matrix, the control segments are maximally overlapped (segment 1 is years 1–46 of the control sequence, segment 2 is 2–47, etc.).
5.4 Two-signal attribution (anthropogenic and natural forcings)
5.4.1 Global mean analysis
First we consider one-layer analyses of temperature change for various depth ranges: 0–100 m, 0–300 m, 0–700 m, 0–1000 m and 0–2000 m. The best-estimate scaling factors and uncertainty for ANT and NAT forcings using spatially complete and sub-sampled fields are shown in Fig. 10. Both ANT and NAT signals are detected (the scaling factor uncertainty is inconsistent with zero) for all depth ranges in all datasets (ORAS4, EN4GR, EN4L and IK09) for both full and sub-sampled fields, with the exception of the 0-1500 m range for IK09 using spatially complete fields.
The uncertainty of the scaling factors is greater in the sub-sampled fields, consistent with the increase in variance upon sub-sampling (Sect. 4). For the upper layers (0–100 m and 0–300 m), where the observational coverage is best, both \(\beta _{ANT}\) and \(\beta _{NAT}\) are generally consistent with unity but the best estimate is usually less than unity (consistent with previous attribution studies, (e.g. Weller et al. 2016)). For the spatially complete fields, although not for the sub-sampled fields, \(\beta _{ANT} < 1\) for the upper 300 m, to match the strong cooling that occurs in the Tropical Pacific and Indian Oceans (see Sect. 2). For the deeper layers (0–700, 0–1000 and 0–2000), the spatially complete and sub-sampled fields exhibit different behaviour. In the spatially complete fields, \(\beta _{ANT} < 1\), except for ORAS4 for the 0–2000, but for the sub-sampled fields \(\beta _{ANT} > 1\), consistent with our inference of a sampling bias towards the North Atlantic where the warming is greatest (Sect. 4). For both spatially complete and sub-sampled fields, \(\beta _{NAT} \ge 1\) in the deeper layers, indicating insufficiently deep penetration of volcanic variability in the model simulations.
The scaling factors for two-layer and three-layer fingerprints (Fig. 11) have smaller uncertainty than for single layers, because of the extra constraint from the vertical structure. Both the ANT and NAT signals are detected for all depth levels and datasets for both spatially complete and sub-sampled fields, except IK09. If only the upper 300 m are covered, \(\beta _{ANT} < 1\) as for one-level fingerprints. With deeper layers, however, both the ANT and NAT scaling factors are consistent with unity in most cases. The spatially complete and sub-sampled fields show similar results, but again the uncertainty of the scaling factors for the sub-sampled fields is slightly larger, so the scaling factors are consistent with unity in more cases.
5.4.2 Regional analysis
With one-layer fingerprints for individual basins not all the signals are always detected, depending on the observational products and whether the fields are subsampled (Fig. 12 shows 0–300 m as an example). Using spatially complete fields the ANT signal is always detected and consistent with unity in the Atlantic, and in most cases in the Pacific, but not always in the Indian and Southern Ocean. The NAT signal is detected in the Pacific basin and Southern Ocean (except in IK09) in all cases, but not for the rest of basins. Overall, using sub-sampled fields means that signals are detected more frequently. As before, using multiple layers constrains the uncertainty of the scaling factors and the signals are detected for almost all depths for all datasets for both spatially complete and sub-sampled fields.
In general the ANT scaling factors for the upper Pacific and Indian Oceans are less than unity because of the observed cooling in the southern part of the tropics (Sect. 3). Therefore we consider a global mean fingerprint excluding the Pacific Ocean between 10\(^{\circ }\)N and 30\(^{\circ }\)S and the Indian Ocean north of 30\(^{\circ }\)S, to cut out the region of cooling, which may be due to unforced variability. With this fingerprint, the ANT signal is detected in all cases and mostly consistent with unity (not shown). However, the NAT signal is not detected in any case, implying that most of the volcanic signal is found in the tropical Pacific Ocean. This is consistent as well with the analysis of individual regions.
We also consider a common fingerprint for multiple regions by concatenating the Atlantic, Pacific, Indian and Southern Oceans. The results (not shown) are very similar to using global mean fingerprints, but the scaling factors tend to be smaller and some signals that were consistent with unity now have significantly less than unity, because considering multiple regions reduces the uncertainty of the scaling factors.
5.4.3 Residual consistency test
Allen and Tett (1999) proposed, as a consistency check, to compare the residuals of the best-estimate combination of signals with unforced variability from the independent estimate of the noise \(C_{N_{2}}\). The failure of this test means that the noise estimate is too large or too small, or that the simulated patterns of response are systematically, rather than statistically, in error, in which case the discrepancy will contribute to the residual. (A systematic error in the amplitudes of the patterns, if the patterns themselves are realistic, will not cause the check to fail, since the scaling factors will correct it). The residual consistency test fails in most cases discussed (crosses on the left side of Figs. 10, 11 and 12). The test succeeds the upper 100 m alone and for some individual basins, most frequently the Atlantic. This is probably because the Atlantic and the upper 100 m are the best observed, and agrees with Weller et al. (2016), who show consistency for the upper 220 m in the Atlantic. In the case of the Southern Ocean, for one-layer analyses for both spatially complete and sub-sampled fields, the residual consistency test passes for all depths in ORAS4 (Fig. 12), but not in the other products. In contrast to the Atlantic, the Southern Ocean is the region that is least observed, thus the most of the pattern is due to the ocean model in the reanalysis.
Given that both spatially complete and sub-sampled fields fail the residual consistency check, this may suggest that the cause is not observational sampling or infilling method, assuming the sub-sampled fields are not affected by observational uncertainty significantly. In all cases of failure, the variance of the residuals is larger than simulated unforced variance. This could be due to a model underestimate of the magnitude of unforced variability, or to model systematic errors in the forced pattern (a systematic error in the amplitudes of the patterns, if the patterns themselves are realistic, will however not cause the check to fail, since the scaling factors will correct it).
If we assume that simulated unforced variability has a realistic spatiotemporal pattern, we may correct its magnitude by applying a scaling factor. It is desirable also to allow for errors in the fingerprints (the patterns of forced response, (c.f. Huntingford et al. 2006). A simple method is to inflate the estimates of unforced variance by an another appropriate factor, assuming that the model errors have the same patterns as variability. To deal with both these possibilities at once we use F-ratio of the residual consistency test (variance of the residuals divided by control variance) as a scaling factor for \(C_{N}\) and \(C_{N_{2}}\).
The consistency test can no longer be used as such (because it is is forced to pass, in effect). The best estimates of beta remain the same but their uncertainty is increased (dotted uncertainty in Figs. 10, 11 and 12), especially for spatially complete fields. For instance, in one-layer and multi-layer global analyses with spatially complete fields, the ANT and NAT signals generally cannot be detected after scaling when layers below 300 m are included (the larger uncertainty makes beta consistent with zero), except in ORAS4, but with the sub-sampled fields the signals are still detected. The uncertainty of the scaling factors for ORAS4 does not increase as much as for the other observational datasets.
5.5 Three-signal attribution (to greenhouse gas, natural and other anthropogenic forcings)
Finally we carry out a three-fingerprint detection and attribution analysis considering ocean temperature change in time and depth for GHG, NAT and OA. Since we do not have simulations for OA forcings only, we deduce the OA scaling factor (\(\beta _{OA}\)) using the historical simulations, by making a linear combination of the historical, historicalNat and historicalGHG scaling factors (\(\beta _{hist}\), \(\beta _{histNat}\), \(\beta _{histGHG}\) respectively). has been widely investigated in previous detection and attribution studies of surface air temperature (e.g. Tett et al. 1999; Stott et al. 2001, 2003; Gillett et al. 2012; Stott and Jones 2012; Jones et al. 2013), but not of ocean temperature change. In this section we present only the analyses with multiple layers, since these give smaller uncertainty in the scaling factors, as in the two-signal case (Sect. 5.4).
5.5.1 Global mean analysis
All three signals are detected in many cases, but more are detected with sub-sampled than with spatially complete fields (Fig. 13). The uncertainties of the beta factors are generally smaller than in the two-signal analyses (Fig. 11), indicating that the extra degree of freedom improves the fit and reduces the contribution of misfit to the residual. As for the two-signal analyses, the residual consistency check almost always fails, and scaling the unforced variability estimates by the F-ratio increases the uncertainty of the scaling factors. After scaling, most signals are no longer detected in spatially complete fields, but in sub-sampled fields the uncertainties do not increase as much and in general the signals are still detected (Fig. 13e–h).
An issue that typically arises when considering this three-signal combination is that the GHG and OA signals tend to be degenerate (e.g. Allen et al. 2006), because they have a similar spatiotemporal pattern, although of different magnitude and opposite sign. This is shown by plotting the joint distribution of the \(\beta\) factors (Fig. 14, in which the crosses show the best guess and the ellipses enclose 90\(\%\) confidence regions). For the GHG and OA signals, the distribution is strongly tilted, indicating that the signals are correlated, that is, if one of the signals is underestimated or overestimated the other signal will have the same behaviour. This means that, although three signals can be detected, these two are not entirely independent.
5.5.2 Regional analysis
With fingerprints simultaneously considering four regions and multiple layers, all three signals are detected in most cases (Fig. 15) with \(\beta \ge 1\). After the noise estimate has been scaled by the F-ratio, the signals are still detectable, in sub-sampled fields. Detection is possible in more cases than for the global mean analysis (Fig. 13) and the uncertainty of the scaling factors is smaller, indicating that the extra discrimination of signals by using regional information improves the fit.
Like for the two-fingerprint analysis, we consider geographical regions with the objective of determining whether the GHG and OA could be better discriminated. Since the temporal structure of the warming may be different in both hemispheres we considered a Northern Hemisphere and Southern Hemisphere fingerprint, but no benefit is found even though the three signals are detected in most cases, showing the same behaviour as previous analysis.
6 Summary and conclusions
We have compared observed ocean temperature change since the 1960s in four datasets, which apply different instrumental corrections and infilling methods for data gaps, with simulations of historical temperature change from CMIP5 AOGCMs. Over this period, warming of the ocean is observed to have gradually spread from the surface downwards, consistent with the model response to increasing GHG, partly offset by anthropogenic aerosols. The warming penetrates more deeply in models than in observations, perhaps connected with the model stratification being too weak, and there is a large spread among models in the magnitude of ocean heat uptake (i.e. Cheng et al. 2016; Gleckler et al. 2016). Major volcanic eruptions caused abrupt cooling which persists for a few years in the upper 500 m in both models and observations, but deeper layers are not affected.
In both observations and models, the warming is greatest in the North Atlantic, except for the northern subpolar gyre, and the northern part of the Southern Ocean. The vertical structure of the warming varies among region, and in both the North Atlantic and Southern Ocean the heat has penetrated deepest while warming is shallow (upper 100 m) in the Pacific and Indian Oceans; these differences are related to the regional processes of OHC change and storage redistribution. Apart from these features, there are few similarities in the geographical distributions of the CMIP5 models and observations. Cooling is observed in the subpolar North Atlantic, whereas historical simulations show enhanced warming. The Pacific Ocean has also warmed on average at the surface in both observations and in model due to increasing GHG concentration, but surface cooling is observed in the western tropical Pacific and Indian Oceans, with subsurface cooling in some low-latitude areas of these basins. These features are not present in the simulations under any forcing.
To assess whether observed changes are consistent with those expected from external forcings (according to models), we have used the technique of optimal fingerprinting. Optimal fingerprinting uses multiple linear regression to compare the observed change with a combination of simulated changes, and produces scaling factors which should be applied to the simulated change to give the best fit to the observed. The novelty of our method is to consider fingerprints in which ocean temperature change is a function of both depth and time simultaneously, so that the propagation of the signal from the surface will be taken into account. Annual resolution is necessary in order to discern the cooling episodes following major volcanic eruptions. We construct the fingerprints from the CMIP5 multi-model mean, rather than individual models, to reduce contamination by unforced variability and systematic errors.
For attribution to specific forcings, we use CMIP5 historical simulations with GHG and with NAT forcings only, as well as those with all historical forcings, which include OA forcings, especially anthropogenic aerosol, as well as GHG and NAT. This is the first time that a three-fingerprint analysis has been carried out, to attribute ocean temperature change to a combination of GHG, OA and NAT forcings. Our analysis strengthens the conclusion of previous studies that the observed ocean warming since the 1960s is of anthropogenic (ANT) origin and cannot be explained by NAT alone or by internally generated variability in the absence of external forcing. Moreover the fingerprints of GHG, OA and NAT can be simultaneously detected, due to their different spatiotemporal structures, although GHG and OA are partly degenerate, despite being of opposite sign and of different magnitude, because their patterns of response are somewhat similar. In the future GHG and OA will become more clearly distinguishable since anthropogenic aerosols started to decrease in the 1980s (e.g. Myhre et al. 2013).
In general, we find that the external forcings are detected more effectively, that the scaling factors are more likely to be consistent with unity, and that the uncertainties of the scaling factors are smaller (i.e. simulated and observed changes are of consistent magnitude), when we consider three fingerprints (GHG, OA and NAT) rather than two (ANT and NAT), when we use fingerprints with multiple depth layers rather than a single layer, and when we distinguish the major ocean basins rather than using the global mean. Refining the fingerprints yields improvements because more information is being used to constrain the scalings, and allowing more degrees of freedom in the forcing reduces any misfit.
Similar improvements come about in the fingerprinting also if we subsample the model fields in the same way as the observations. We suggest that this is because the observational sampling is biased, probably towards portions of the ocean which have warmed more (the Atlantic and the upper ocean). When sub-sampled consistently, the observational products show greater similarities among themselves as well, especially evident in their temporal variation, implying that the infilling methods make the largest contribution to the spread among them. With sub-sampling, both observational products and CMIP5 models have greater temporal variability, especially in the regions that have fewer observations (earlier in the record and deeper layers).
When layers below 100 m are considered, the variance of the regression residuals from the optimal fingerprinting (i.e. the difference between simulated and observed change) is statistically significantly greater than unforced variability simulated by CMIP5 models. This could be because CMIP5 models simulate too little unforced ocean temperature variability, or because of systematic errors in the simulated response to forcing. If we inflate the estimate of unforced variance to match the residuals, the uncertainties of the scaling factors consequently increase, but the signals are nonetheless still detectable. However, this difficulty shows the limitations of the detection and attribution procedure. Further work is required to understand the physical process responsible for the spatio-temporal patterns, in order to establish why models and observations do not agree, for example the surface cooling in the Atlantic subpolar gyre and the subsurface cooling in the Pacific. Understanding such processes is essential to improve our confidence in projections of the future.
Unfortunately historical simulations by the CMIP5 models ended in 2005, so the much better ocean sampling afforded by the complete deployment of the Argo floats could not be fully exploited in this work. Future studies could go beyond our analysis in this respect, and also by taking advantage of CMIP6 (Eyring et al. 2016). CMIP6 will bring the benefits of the most recent model developments, the detection and attribution model intercomparison project (DAMIP Gillett et al. 2016), historical simulations ending in 2014, more ensemble members and longer piControl simulations. Furthermore, updating the analysis may also allow a more effective discrimination between the GHG and OA signals, due to the different temporal evolution of the forcings, although it will probably not improve detection of the NAT signal, since there has not been a major volcanic eruption since Pinatubo.
References
Abraham JP, Baringer M, Bindoff NL, Boyer T, Cheng LJ, Church JA, Conroy JL, Domingues CM, Fasullo JT, Gilson J, Goni G, Good SA, Gorman JM, Gouretski V, Ishii M, Johnson GC, Kizu S, Lyman JM, Macdonald AM, Minkowycz WJ, Moffitt SE, Palmer MD, Piola AR, Resegetti F, Schuckmann K, Trenberth KE, Velicogna I, Willis JK (2013) A review of global ocean temperature observations: implications for ocean heat content estimates and climate change. Rev Geophys 51(3):450–483. https://doi.org/10.1002/rog.20022
AchutaRao KM, Santer BD, Gleckler PJ, Taylor KE, Pierce DW, Barnett TP, Wigley TML (2006) Variability of ocean heat uptake: reconciling observations and models. J Geophys Res: Oceans 111(C5)
AchutaRao KM, Ishii M, Santer BD, Gleckler PJ, Taylor KE, Barnett TP, Pierce DW, Stouffer RJ, Wigley TML (2007) Simulated and observed variability in ocean temperature and heat content. Proc Natl Acad Sci USA 104:10,768–10,773
Allen MR, Stott PA (2003) Estimating signal amplitudes in optimal fingerprinting I: estimation theory. Clim Dyn 21:477–491
Allen MR, Tett SFB (1999) Checking for model consistency in optimal finger printing. Clim Dyn 15:419–434
Allen MR, Gillett NP, Kettleborough JA, Hegerl G, Schnur R, Stott PA, Boer G, Covery G, Delworth TL, Jones GS, Mitchell JFB, Barnett TP (2006) Quantifying anthropogenic influence on recent near-surface temperature change. Surv Geophys 27:491–454
Armour KC, Marshall J, Scott JR, Donohoe A, Newsom ER (2016) Southern ocean warming delayed by circumpolar upwelling and equatorward transport. Nat Geosci. https://doi.org/10.1038/ngeo2731
Balmaseda MA, Mogensen K, Weaver AT (2012) Evaluation of the ECMWF ocean reanalysis system ORAS4. Q J R Meteorol Soc 10:623–643. https://doi.org/10.1002/qj.2063
Balmaseda MA, Trenberth KE, Klln E (2013) Distinctive climate signals in reanalysis of global ocean heat content. Geophys Res Lett. https://doi.org/10.1002/grl.50382
Barnett TP, Pierce DW, Schnur R (2001) Detection of anthropogenic climate change in the world’s oceans. Science 292:270–274
Barnett TP, Pierce DW, AchutaRao KM, Gleckler PJ, Santer BD, Gregory JM, Washington WM (2005) Penetration of human-induced warming into the world’s oceans. Science 309:284–287
Bouttes N, Gregory JM, Kuhlbrodt T, Suzuki T (2012) The effect of windstress change on future sea level change in the Southern Ocean. Geophys Res Lett 39(L23):602. https://doi.org/10.1029/2012GL054207
Boyer T, Domingues CM, Good SA, Johnson GC, Lyman JM, Ishii M, Gouretski V, Willis JK, Antonov J, Wijffels S, Church JA, Cowley R, Bindoff NL (2016) Sensitivity of global upper-ocean heat content estimates to mapping methods, xbt bias corrections, and baseline climatologies. J Clim 29(13):4817–4842. https://doi.org/10.1175/JCLI-D-15-0801.1
Cai W (2006) Antarctic ozone depletion causes an intensification of the southern ocean super-gyre circulation. Geophys Res Lett 33(L03):712. https://doi.org/10.1029/2005GL024911
Cheng L, Zhu J (2014) Artifacts in variations of ocean heat content induced by the observation system changes. Geophys Res Lett 41(20):7276–7283
Cheng L, Trenberth KE, Palmer MD, Zhu J, Abraham JP (2016) Observed and simulated full-depth ocean heat-content changes for 1970–2005. Ocean Sci 12(4):925–935
Church JA, White NJ, Arblaster JM (2005) Significant decadal-scale impact of volcanic eruptions on sea level and ocean heat content. Nature 438:74–77. https://doi.org/10.1038/nature04237
Delworth TL, Ramaswamy V, Stenchikov GL (2005) The impact of aerosols on simulated global ocean temperature and heat content in the 20th century. Geophys Res Lett 32(L24):709. https://doi.org/10.1029/2005GL024457
Ding Y, Carton JA, Chepurin GA, Stenchikov G, Robock A, Sentman LT, Krasting JP (2014) Ocean response to volcanic eruptions in coupled model intercomparison project 5 simulations. J Geophys Res Oceans 119(9):5622–5637
Domingues CM, Church JA, White NJ, Gleckler PJ, Wijffels SE, Barker PM, Dunn JR (2008) Improved estimates of upper-ocean warming and multi-decadal sea-level rise. Nature 453(7198):1090. https://doi.org/10.1038/nature07080
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci Model Develop 9(5):1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Ferreira D, Marshall J, Bitz CM, Solomon S, Plumb A (2015) Antarctic ocean and sea ice response to ozone depletion: a two-time-scale problem. J Clim 28(3):1206–1226. https://doi.org/10.1175/JCLI-D-14-00313.1
Fyfe JC, Saenko OA, Zickfeld K, Eby M, Weaver AJ (2007) The role of poleward-intensifying winds on Southern Ocean warming. J Clim 20:5391–5400. https://doi.org/10.1175/2007JCLI1764.1
Gent PR, Danabasoglu G (2004) Heat uptake and the thermohaline circulation in the community climate system model, version 2. J Clim 17(20):4058–4069
Gillett NP, Zwiers FW, Weaver AJ, Hegerl GC, Allen MR, Stott PA (2002) Detecting anthropogenic influence with a multi-model ensemble. Geophys Res Lett (in press)
Gillett NP, Arora VK, Flato GM, Scinocca JF, von Salzen K (2012) Improved constraints on 21st-century warming derived using 160 years of temperature observations. Geophys Res Lett 39(1). https://doi.org/10.1029/2011GL050226 (l01704)
Gillett NP, Shiogama H, Funke B, Hegerl G, Knutti R, Matthes K, Santer BD, Stone D, Tebaldi C (2016) The detection and attribution model intercomparison project (DAMIP v1.0). Geosci Model Develop 9(10):3685–3697. https://doi.org/10.5194/gmd-9-3685-2016
Gleckler PJ, AchutaRao K, Gregory JM, Santer BD, Taylor KE, Wigley TML (2006a) Krakatoa lives: the effect of volcanic eruptions on ocean heat content and thermal expansion. Geophys Res Lett 33(L17):702. https://doi.org/10.1029/2006GL026771
Gleckler PJ, Wigley TML, Santer BD, Gregory JM, AchutaRao K, Taylor KE (2006b) Krakatoa’s signature persists in the ocean. Nature 439:675. https://doi.org/10.1038/439675a
Gleckler PJ, Santer BD, Domingues CM, Pierce DW, Barnett TP, Church JA, Taylor KE, AchutaRao KM, Boyer TP, Ishii M, Caldwell PM (2012) Human-induced global ocean warming on multidecadal timescales. Nat Clim Change 2(7):524–529. https://doi.org/10.1038/nclimate1553
Gleckler PJ, Durack PJ, Stouffer RJ, Johnson GC, Forest CE (2016) Industrial-era global ocean heat uptake doubles in recent decades. Nat Clim Change. https://doi.org/10.1038/nclimate2915
Good S (2016) The impact of observational sampling on time series of global 0–700 m ocean average temperature: a case study. Int J Clim
Good SA, Martin MJ, Rayner NA (2013) EN4: quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J Geophys Res 118:6704–6716. https://doi.org/10.1002/2013JC009067
Gouretski V, Koltermann KP (2007) How much is the ocean really warming? Geophys Res Lett 34(L01):610. https://doi.org/10.1029/2006GL027834
Gouretski V, Reseghetti F (2010) On depth and temperature biases in bathythermograph data: Development of a new correction scheme based on analysis of global ocean database. Deep-Sea Res I. https://doi.org/10.1016/j.dsr.2010.03.011
Gregory JM (2010) Long-term effect of volcanic forcing on ocean heat content. Geophys Res Lett 37(L22):701. https://doi.org/10.1029/2010GL045507
Gregory JM, Forster PM (2008) Transient climate response estimated from radiative forcing and observed temperature change. J Geophys Res 113(D23):105. https://doi.org/10.1029/2008JD010405
Gregory JM, Banks HT, Stott PA, Lowe JA, Palmer MD (2004) Simulated and observed decadal variability in ocean heat content. Geophys Res Lett 31(L15):312. https://doi.org/10.1029/2004GL020258
Gregory JM, Lowe JA, Tett SFB (2006) Simulated global-mean sea-level changes over the last half-millennium. J Clim 19:4576–4591
Gregory JM, Bi D, Collier MA, Dix MR, Hirst AC, Hu A, Huber M, Knutti R, Marsland SJ, Meinshausen M, Rashid HA, Rotstayn LD, Schurer A, Church JA (2013) Climate models without pre-industrial volcanic forcing underestimate historical ocean thermal expansion. Geophys Res Lett 40:1–5. https://doi.org/10.1002/grl.50339
Hansen J, Sato M, Nazarenko L, Ruedy R, Lacis A, Koch D, Tegen I, Hall T, Shindell D, Santer B, Stone P, Novakov T, Thomason L, Wang R, Wang Y, Jacob D, Hollandsworth-Frith S, Bishop L, Logan J, Thompson A, Stolarski R, Lean J, Willson R, Levitus S, Antonov J, Rayner N, Parker D, Christy J (2002) Climate forcings in Goddard Institute for Space Studies SI2000 simulations. J Geophys Res 107. https://doi.org/10.1029/2001JD001143
Hasselmann K (1979) On the signal-to-noise problem in atmospheric response studies. In: Shaw DB (ed) Meteorology over the tropical oceans, Royal Meteorological Society, pp 251–259
Hasselmann K (1993) Optimal fingerprints for the detection of time dependent climate change. J Clim 6:1957–1971
Hasselmann K (1997) On multifingerprint detection and attribution of anthropogenic climate change. Clim Dyn 13:601–611
Hegerl CG, Hasselmann K, Cubasch U, Mitchell BJF, Roeckner E, Voss R, Waszkewitz J (1997) Multi-fingerprint detection and attribution analysis of greenhouse gas, greenhouse gas-plus-aerosol and solar forced climate change. Clim Dyn 13(9):613–634. https://doi.org/10.1007/s003820050186
Hegerl GC, von Storch H (1996) Applying coupled ocean-atmosphere models for predicting, detecting and specifying climate change (accepted by ZAMM)
Hegerl GC, Jones PD, Barnett TP (2001) Effect of observational sampling error on the detection of anthropogenic climate change. J Clim 14:198–207
Huntingford C, Stott PA, Allen MR, Lambert FH (2006) Incorporating model uncertainty into attribution of observed temperature change. Geophys Res Lett 33. https://doi.org/10.1029/2005GL024831
Ishii M, Kimoto M (2009) Reevaluation of historical ocean heat content variations with time-varying XBT and MBT depth bias corrections. Oceanography 65:287–299
Jones GS, Stott PA, Christidis N (2013) Attribution of observed historical near surface temperature variations to anthropogenic and natural causes using cmip5 simulations. J Geophys Res 18(10):4001–4024. https://doi.org/10.1002/jgrd.50239
Knutti R (2010) The end of model democracy? Clim Change. https://doi.org/10.10007/s10584-010-9800-2
Knutti R, Masson D, Gettelman A (2013) Climate model genealogy: generation cmip5 and how we got there. Geophys Res Lett 40(6):1194–1199. https://doi.org/10.1002/grl.50256
Kuhlbrodt T, Gregory JM (2012) Ocean heat uptake and its consequences for the magnitude of sea level rise and climate change. Geophys Res Lett 39(L18):608. https://doi.org/10.1029/2012GL052952
Levitus S, Antonov JI, Boyer TP, Stephens C (2000) Warming of the world ocean. Science 287:2225–2229
Levitus S, Antonov JI, Wang J, Delworth TL, Dixon KW, Broccoli AJ (2001) Anthropogenic warming of the Earth’s climate system. Science 292:267–270
Levitus S, Antonov J, Boyer T (2005) Warming of the world ocean, 1955–2003. Geophys Res Lett 32(L02):604. https://doi.org/10.1029/2004GL021592
Levitus S, Antonov JI, Boyer TP, Baranova OK, Garcia HE, Locarnini RA, Mishonov AV, Reagan JR, Seidov D, Yarosh ES, Zweng MM (2009) Global ocean heat content 1955–2008 in light of recently revealed intrumentation problems. Geophys Res Lett 36. https://doi.org/10.1029/2008GL037155
Levitus S, Antonov JI, Boyer TP, Locarnini RA, Garcia HE, Mishonov AV (2012) World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys Res Lett 39
Llovel W, Fukumori I, Meyssignac B (2013) Depth-dependent temperature change contributions to global mean thermosteric sea level rise from 1960 to 2010. Global and Planetary Change 101:113–118. https://doi.org/10.1016/j.gloplacha.2012.12.011. http://www.sciencedirect.com/science/article/pii/S0921818112002391
Lyman JM, Johnson GC (2008) Estimating annual global upper-ocean heat content anomalies despite irregular in situ ocean sampling. J Clim 21(21):5629–5641. https://doi.org/10.1175/2008JCLI2259.1
Lyman JM, Johnson GC (2014) Estimating global ocean heat content changes in the upper 1800 m since 1950 and the influence of climatology choice. J Clim 27(5):1945–1957. https://doi.org/10.1175/JCLI-D-12-00752.1
Lyman JM, Good SA, Gouretski VV, Ishii M, Johnson GC, Palmer MD, Smith DM, Willis JK (2010) Robust warming of the global upper ocean. Nature 465:334–337. https://doi.org/10.1038/nature09043
Mogensen K, Balmaseda MA, Weaver AT (2012) The nemovar ocean data assimilation system as implemented in the ecmwf ocean analysis for system 4’. Tech Memo 668 ECMWF: Reading, UK
Myhre G, Shindell D, Bréon FM, Collins W, Fuglestvedt J, Huang J, Koch D, Lamarque JF, Lee D, Mendoza B, Nakajima T, Robock A, Stephens G, Takemura T, Zhang H (2013) Anthropogenic and natural radiative forcing. In: Stocker DQGKPMTSAJBANYXVB TF, (eds) PM (eds) Climate Change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge and New York
Palmer MD, Brohan P (2011) Estimating sampling uncertainty in fixed-depth and fixed-isotherm estimates of ocean warming. Int J Climatol 15(7):980–986. https://doi.org/10.1002/joc.2224
Palmer MD, Haines K (2009) Estimating oceanic heat content change using isotherms. J Clim 22(19):4953–4969. https://doi.org/10.1175/2009JCLI2823.1
Palmer MD, Haines K, Ansell TJ, Tett SFB (2007) Isolating the signal of ocean global warming. Geophys Res Lett 34. https://doi.org/10.1029/2007GL031712
Palmer MD, Good SA, Haines K, Rayner NA, Stott PA (2009) A new perspective on warming of the global oceans. Geophys Res Lett
Palmer MD, Roberts CD, Balmaseda M, Chang YS, Chepurin G, Ferry N, Fujii Y, Good SA, Guinehut S, Haines K, Hernandez F, Köhl A, Lee T, Martin MJ, Masina S, Masuda S, Peterson KA, Storto A, Toyoda T, Valdivieso M, Vernieres G, Wang O, Xue Y (2015) Ocean heat content variability and change in an ensemble of ocean reanalyses. Climate Dynamics pp 1–22. https://doi.org/10.1007/s00382-015-2801-0
Palmer MD, Roberts CD, Balmaseda M, Chang YS, Chepurin G, Ferry N, Fujii Y, Good SA, Guinehut S, Haines K, Hernandez F, Köhl A, Lee T, Martin MJ, Masina S, Masuda S, Peterson KA, Storto A, Toyoda T, Valdivieso M, Vernieres G, Wang O, Xue Y (2017) Ocean heat content variability and change in an ensemble of ocean reanalyses. Clim Dyn 49(3):909–930. https://doi.org/10.1007/s00382-015-2801-0
Pennell C, Reichler T (2011) On the effective number of climate models. J Clim 24(9):2358–2367. https://doi.org/10.1175/2010JCLI3814.1
Pierce DW, Barnett TP, AchutaRao KM, Gleckler PJ, Gregory JM, Washington WM (2006) Anthropogenic warming of the oceans: observations and model results. J Clim 19:1873–1900
Pierce DW, Gleckler PJ, Barnett TP, Santer BD, Durack PJ (2012) The fingerprint of human-induced changes in the ocean’s salinity and temperature fields. Geophys Res Lett 39(21)
Reichert BK, Schnur R, Bengtsson L (2002) Global ocean warming tied to anthropogenic forcing. Geophys Res Lett 29. https://doi.org/10.1029/2001GL013954
Reichler T, Kim J (2008) How well do coupled models simulate today’s climate? Bull Am Meteorol Soc 89(3):303–311. https://doi.org/10.1175/BAMS-89-3-303
Robock A (2000) Volcanic eruptions and climate. Rev Geophys 38(2):191–219
Roemmich D, John Gould W, Gilson J (2012) 135 years of global ocean warming between the challenger expedition and the argo programme. Nat Clim Change 2(6):425–428. https://doi.org/10.1038/nclimate1461
Roemmich D, Church J, Gilson J, Monselesan D, Sutton P, Wijffels S (2015) Unabated planetary warming and its ocean structure since 2006. Nat Clim Change 5(3):240–245. https://doi.org/10.1038/nclimate2513
Sedláček J, Knutti R (2012) Evidence for external forcing on 20th-century climate from combined ocean-atmosphere warming patterns. Geophys Res Lett 39(20)
Sen Gupta A, Jourdain NC, Brown JN, Monselesan D (2013) Climate drift in the cmip5 models. J Clim 26:8597–8615. https://doi.org/10.1175/JCLI-D-12-00521.1
Storch H, Zwiers F (2012) Testing ensembles of climate change scenarios for “statistical significance”. Clim Change 117(1):1–9. https://doi.org/10.1007/s10584-012-0551-0
Stott PA, Jones GS (2012) Observed 21st century temperatures further constrain likely rates of future warming. Atmos Sci Lett 13(3):151–156. https://doi.org/10.1002/asl.383
Stott PA, Tett SFB, Jones GS, Allen MR, Ingram WJ, Mitchell JFB (2001) Attribution of twentieth century temperature change to natural and anthropogenic causes. Clim Dyn 17:1–21
Stott PA, Allen MR, Jones GS (2003) Estimating signal amplitudes in optimal fingerprinting. part ii: application to general circulation models. Clim Dyn https://doi.org/10.1007/s00382-002-0300-6
Sun S, Hansen JE (2003) Climate simulations for 1951–2050 with a coupled atmosphere-ocean model. J Clim 16:2807–2826
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Tebaldi C, Knutti R (2007) Review the use of the multi-model ensemble in probabilistic climate projections. Philos Trans R Soc Lond 365(1857):2053–2076
Tett SFB, Stott PA, Allen MR, Ingram WJ, Mitchell JFB (1999) Causes of twentieth-century temperature change near the earth’s surface. Nature 399:569–572
Tett SFB, Jones GS, Stott PA, Hill DC, Mitchell JFB, Allen MR, Ingram WJ, Johns TC, Johnson CE, Jones A, Roberts DL, Sexton DMH, Woodage MJ (2002) Estimation of natural and anthropogenic contributions to 20th century temperature change. J Geophys Res 107. https://doi.org/10.1029/2000JD000028
Thorne P (2001) Advancing climate change detection and attribution studies in the free atmosphere. PhD thesis, University of East Anglia
Trenberth KE (2010) Global change: the ocean is warming, isn’t it? Nature 465(7296):304–304. https://doi.org/10.1038/465304a
Weller E, Min SK, Palmer MD, Lee D, Yim BY, Yeh SW (2016) Multi-model attribution of upper-ocean temperature changes using an isothermal approach. Sci Rep 6:26,926 EP. https://doi.org/10.1038/srep26926
Willis JK, Roemmich D, Cornuelle B (2004) Interannual variability in upper ocean heat content, temperature, and thermosteric expansion on global scales. J Geophys Res: Oceans 109(C12)
Acknowledgements
We thank Rowan Sutton and John Church for their useful suggestions. For their roles in producing, coordinating, and making available the CMIP5 model output, we acknowledge the climate modelling groups, the World Climate Research Programmes (WCRP) Working Group on Coupled Modelling (WGCM), and the GlobalOrganization for Earth SystemScience Portals (GO-ESSP). We also acknowledge ECMWF, the MetOffice, S. Levitus and M. Ishii for making available the ocean temperature products. R. Bilbao was supported by the Natural Environmental Research Council (CASE studentship 1224799) and MetOffice.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Pre-industrial control drift removal
An important issue regarding the pre-industrial control simulations of CMIP5 AOGCMs is the spurious trends which are present, especially in the deep ocean. These are referred to as ‘climate’ or ‘control’ drift (e.g. Sen Gupta et al. 2013) and arise because climate models require centennial time-scales to reach equilibrium, determined by the time it takes for anomalies to be advected or mixed in the deep ocean. However, due to the complexity of climate models, spin-up times are insufficient due to the limited computational resources and time constraints of modelling centres (Sen Gupta et al. 2013).
In the upper layers of the ocean climate drift may be neglected as the surface equilibrates on short time-scales; however in the deeper ocean, due to the larger transport timescales, climate drift is common as shown in Fig. 16a for individual CMIP5 AOGCMs. It can be approximately estimated by fitting a linear or higher order polynomial in time and then subtracting it from the simulation (Sen Gupta et al. 2013). As shown in Figs. 16b and c subtracting a linear or higher order polynomial is non-trivial and there is a compromise between keeping unrealistic low frequency variability (linear fit) or subtracting genuine variability on centennial and multi-centennial timescales (higher order polynomials). We choose to subtract a 4th order polynomial. To reduce computational time, the climate drift in control simulations is estimated and subtracted after calculating the volume average; this has the advantage of averaging out spatial variability, making the drift more apparent.
Historical simulations with external forcings (historical, historicalNat and HistoricalGHG in this case) are initialised from a particular year in the pre-industrial control simulations and therefore the pre-industrial control drift also affects the historical simulations. To remove the drift from the historical runs we assume the forced runs contain the same drift as the pre-industrial control. To correct for the drift when calculating forced temperature change, the temporal fit to annual means of the equivalent period in the pre-industrial control run is subtracted. For this, estimating a linear fit is sufficient, since the historical experiments are fairly short, and the reason for using a fit, rather than the pre-industrial control run itself, is to avoid increasing the inter-annual variability of temperature change.
Appendix 2: Volcanic drift removal
Previous studies using AOGCMs show that ocean heat content decreases abruptly after each volcanic eruption and subsequently recovers slowly (Robock 2000; Church et al. 2005; Delworth et al. 2005; Gleckler et al. 2006a, b; Gregory et al. 2006, 2013; Gregory 2010; Ding et al. 2014). Gregory (2010) and Gregory et al. (2013) showed that this continual loss of heat is unrealistic and the result of not including the episodic volcanic forcing in the spin-up of the AOGCMs.
The volcanic drift is calculated by estimating the temporal linear trends from historicalNat simulations (1850–2005) (Fig. 17), after subtracting control drift (Appendix 1), using the ensemble mean of for models which offer a historicalNat ensemble. To determine whether these trends are statistically significantly with respect to unforced internal variability, non-overlapping temporal trends of equal length to 1850–2005 were calculated from pre-industrial control simulations, and their distribution compared with the ‘volcanic drift’. Note this test should be taken with caution since the control runs are typically only a few centuries long and using them to examine variability on centennial time-scales is not very robust. Nevertheless, for several of the models the volcanic drift is greater than simulated by unforced internal variability, justifying its subtraction from historical and historicalNat, which both include volcanic forcing. We thus subtract volcanic drift from all the models with historicalNat simulations available. For some models there is a significant positive (rather than the expected negative) trend relative to the control. The cause of such positive drifts is unknown, and they are subtracted too.
Appendix 3: Sub-sampling observations and CMIP5 models
The EN4 dataset provides a metric of the observational influence on the objective analyses (Good et al. 2013). This metric consists of a value between zero and one for each grid cell, where values close to one indicate strong influence of observations on the analysis and values of zero where there were no observations. Hence it is possible to construct an observational mask by only considering those grid cells that exceed a particular observational influence value. Following Good et al. (2013) we choose a threshold of 0.95. The spatio-temporal mask was then constructed by masking the grid-points with less than 0.95 observational influence for the period 1960–2005. The EN4 dataset consists of monthly means, from which we computed annual means. To calculate the observational mask two methods were compared. The first method takes the maximum value of the observational influence of the 12 months for each gridcell. The second method calculates the annual mean value. The results are very similar and the first method was adopted.
Prior to masking the fields, we make them relative to the time-mean of 1995–2005 which is the best observed time period and therefore gives least chance that the anomalies are constructed with respect to infilled values. This perhaps avoids problems with the artefacts arising from the transition to Argo observations (c.f. Cheng and Zhu 2014). Since the observational mask is on EN4 grid, the ORAS4 and IK09 fields are regridded to the EN4 grid using bilinear interpolation. Then we apply the mask to the potential temperature fields of ORAS4, both EN4 versions and IK09 for the period 1960–2005, but not Lev12 since the data uses a 5-year running mean.
Similarly, CMIP5 models are regridded to the EN4 grid using either bilinear interpolation or triangulation and linear interpolation depending on whether the grids are rectangular or curvilinear. Then anomalies are computed with respect to the mean of 1995–2005 and the EN4 observational mask is applied.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bilbao, R.A.F., Gregory, J.M., Bouttes, N. et al. Attribution of ocean temperature change to anthropogenic and natural forcings using the temporal, vertical and geographical structure. Clim Dyn 53, 5389–5413 (2019). https://doi.org/10.1007/s00382-019-04910-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04910-1