Improving the long-lead predictability of El Niño using a novel forecasting scheme based on a dynamic components model

Abstract

El Niño (EN) is a dominant feature of climate variability on inter-annual time scales driving changes in the climate throughout the globe, and having wide-spread natural and socio-economic consequences. In this sense, its forecast is an important task, and predictions are issued on a regular basis by a wide array of prediction schemes and climate centres around the world. This study explores a novel method for EN forecasting. In the state-of-the-art the advantageous statistical technique of unobserved components time series modeling, also known as structural time series modeling, has not been applied. Therefore, we have developed such a model where the statistical analysis, including parameter estimation and forecasting, is based on state space methods, and includes the celebrated Kalman filter. The distinguishing feature of this dynamic model is the decomposition of a time series into a range of stochastically time-varying components such as level (or trend), seasonal, cycles of different frequencies, irregular, and regression effects incorporated as explanatory covariates. These components are modeled separately and ultimately combined in a single forecasting scheme. Customary statistical models for EN prediction essentially use SST and wind stress in the equatorial Pacific. In addition to these, we introduce a new domain of regression variables accounting for the state of the subsurface ocean temperature in the western and central equatorial Pacific, motivated by our analysis, as well as by recent and classical research, showing that subsurface processes and heat accumulation there are fundamental for the genesis of EN. An important feature of the scheme is that different regression predictors are used at different lead months, thus capturing the dynamical evolution of the system and rendering more efficient forecasts. The new model has been tested with the prediction of all warm events that occurred in the period 1996–2015. Retrospective forecasts of these events were made for long lead times of at least two and a half years. Hence, the present study demonstrates that the theoretical limit of ENSO prediction should be sought much longer than the commonly accepted “Spring Barrier”. The high correspondence between the forecasts and observations indicates that the proposed model outperforms all current operational statistical models, and behaves comparably to the best dynamical models used for EN prediction. Thus, the novel way in which the modeling scheme has been structured could also be used for improving other statistical and dynamical modeling systems.

Appendices

Appendix 1

The linear Gaussian state space model form that we have used is as in de Jong (1991), that is:

$$\begin{aligned} y_t =Z_t\alpha _t+G_t\epsilon _t,\quad \alpha _{t+1} = T_t\alpha _t+H_t\epsilon _t,\quad \epsilon _t\sim {\text{NID}}\left( 0,I\right) , \end{aligned}$$

(6)

for $t=1,\ldots ,n,$ and where $\epsilon _t$ is a vector of serially independent disturbance series. The $m\times 1$ state vector $\alpha _t$ contains the unobserved components and their associated variables.

$$\begin{aligned} & \alpha _t = \left( \mu _t , \gamma _{t}, \gamma _{t-1},\ldots ,\gamma _{t-10},\psi _{1t} , \psi ^+ _{1t}, \psi _{2t} , \psi ^+ _{2t}, \psi _{3t} , \psi ^+ _{3t} , \delta '\right) ^{\prime }, \\ & \epsilon _t = \left( \varepsilon _{t} , \eta _t , \omega _{t}, \kappa _{1t} , \kappa _{1t} ^+ , \kappa _{2t} , \kappa _{2t} ^+ , \kappa _{3t} , \kappa _{3t} ^+\right) ^{\prime }, \end{aligned}$$

The measurement equation is the first equation in (6) and it relates the observation $y_t$ to the state vector $\alpha _t$ through the signal $Z_t \alpha _t$. The transition equation is the second equation in (6) and it is used to formulate the dynamic processes of the unobserved components in a companion form. The deterministic matrices $T_t$, $Z_t$, $H_t$ and $G_t$, are time-invariant except the matrix $Z_t$, and referred to as system matrices that are sparse and known:

$$\begin{aligned} T_t=\, & {} \left[ {\begin{array}{ccccccccccccccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} p(1) &{} q(1) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -q(1) &{} p(1) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} p(2) &{} q(2) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -q(2) &{} p(2) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} p(3) &{} q(3) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -q(3) &{} p(3) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} p(4) &{} q(4) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -q(4) &{} p(4) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} p(5) &{} q(5) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -q(5) &{} p(5) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} c(1) &{} s(1) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -s(1) &{} c(1) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} c(2) &{} s(2) &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -s(2) &{} c(2) &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} c(3) &{} s(3) &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -s(3) &{} c(3) &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} I_k \end{array}} \right] ,\\ H_t=\, & {} \left[ { \begin{array}{ccccccccc} 0 &{} \sigma _{\eta } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \sigma _{\omega } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,1} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,2} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,2} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,3} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{\kappa ,3}\\ 0_k &{} 0_k &{} 0_k &{} 0_k &{} 0_k &{} 0_k &{} 0_k &{} 0_k &{} 0_k \end{array}} \right] , \\ Z_t=\, & {} \left( { \begin{array}{ccccccccccccccccccc} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} x_t' \\ \end{array}} \right) ,\\ G_t=\, & {} \left( { \begin{array}{ccccccccc} \sigma _{\varepsilon } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array}} \right) , \end{aligned}$$

where $0_k$ is a $k\times 1$ vector of zeros, $I_k$ is a $k\times 1$ vector of ones, $p(i) = \cos \lambda _{i}$ and $q(i) = \sin \lambda _{i}$ for $\lambda _{i}=\frac{2\pi i}{S}$, $\hbox {i} = 1,2,\ldots ,\lfloor \frac{S}{2} \rfloor$; $c(j) = \varphi _{\psi ,j} \cos \lambda _{c,j}$ and $s(j) = \varphi _{\psi ,j} \sin \lambda _{c,j}$ for $j=1,2,3$.

Appendix 2

Every explanatory regression variable that has been used in the analysis (surface temperature, subsurface temperature at different depth levels and regions, and zonal wind stress at different regions) has been tested separately with the model described in Sect. 3 during the fitting procedure. In this way each variable was fitted at every lag time between 0 and 35 months. Based on the in-sample estimations for each of these fittings (the sample spanned the data from January 1982 to December 2012), the p value (an indicator of statistical significance, showing the probability that the coefficient of the predictor is equal to zero, and thus that the predictor does not add value), the significance level (SL) based on it ($\hbox {SL}=90\,\%$ for $p\le 0.10$, $\hbox {SL}=95\,\%$ for $p\le 0.05$, $\hbox {SL}=99\,\%$ for $p\le 0.01$), and the $Rs^2$ value (modified coefficient of determination based on seasonal means—the ratio between the variance explained by the model and the variance of the seasonally differenced time series), were used to determine significance of the regression variable at the respective lag time. The significant values obtained in this way are summarized in the following Tables 3, 4, 5 and 6.

Table 3 Diagnostics of wind stress predictor regression variables

Table 4 Diagnostics of surface and subsurface temperature predictor regression variables

Table 5 Diagnostics of subsurface temperature predictor regression variables

Table 6 Diagnostics of subsurface temperature predictor regression variables

Table 7 Predictor regression variables added to the model at lead times between 17 and 36 months, based on the criteria and results shown in Tables 3–6

Table 8 Predictor regression variables added to the model at lead times between 0 and 15 months, based on the criteria and results shown in Tables 3–6

Table 9 Predictions of the January target month for all EN events shown in Fig. 9

Table 10 Correlation between forecasts and observations, and root mean square error (RMSE) as functions of lead month

Fig. 1

Components graphics of the model. Shown are temperature ($^\circ$C) time series of the a level and regression components together with the N3.4 index, b the seasonal component, and the three cycle components of periods: c 1.5, d 2.5, e 4.5 years

Fig. 2

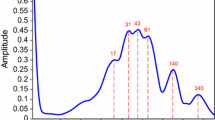
a Multi Taper Method (MTM) power spectra for the observed N3.4 time series. The solid line indicates the power density and dashed lines the respective confidence level (CL) based on a red noise null hypothesis. The red indicators correspond to the near-annual, biannual, and quasi-quadrennial ENSO modes of variability. Reconstructed components from the multitaper decomposition in a, corresponding to the b seasonal, c near-annual, d biannual, e quasi-quadrennial modes

Fig. 3

Pearson correlations between the temporal scores of the first CEOF modes of filtered SSTs and surface wind stress anomalies, and filtered spatio-temporal SST anomalies and wind stress anomalies in the equatorial Pacific region. A Butterworth filter has been applied to the SST and wind stress data sets, so that only frequencies corresponding to periods between 14 and 18 months (associated with the near-annual mode of variability) have been kept. Panels correspond to the respective phases of the CEOF shown on the figure. Shaded areas indicate significant anomalies

Fig. 4

Same as Fig. 3, but the Butterworth filter has been applied so that only frequencies corresponding to periods between 24 and 28 months (associated with the biannual mode of variability) have been kept

Fig. 5

Same as Fig. 3, but the Butterworth filter has been applied so that only frequencies corresponding to periods between 46 and 63 months (associated with the low-frequency mode of variability) have been kept

Fig. 6

Composites of surface zonal wind stress (Nm$^{-2}$, arrows) anomalies with respect to all EN events in the period 1978–2012. Shown are anomalies a 24, b 13, c 7 months before the winter peak of EN. The red boxes indicate the three zonal wind stress regions from Table 1—a Region I, b Region II, c Region III

Fig. 7

Composites of subsurface temperature ($^{\circ }$C, shading) anomalies at a 150, b 250, c 400 m depth with respect to all EN events in the period 1978–2012 in Region I (see Table 2). Data is filtered using a low-pass Butterworth filter (cut-off frequency 18, order 10)

Fig. 8

Same as Fig. 7, but at a surface, b 100, c 200 m depth in Region II (see Table 2)

Fig. 9

Time series of area-averaged sea surface temperature ($^\circ$C) anomalies in the Niño 3.4 region. Shown are forecasts of the a, f, k 1997/98, b, g, l 2002/03, c, h, m 2006/07, d, i, n 2009/10, and e, j, o 2014/15 EN events, starting 29–34 (magenta in a and d), 27–28 (light blue in b–e), 24–26 (dark green in a–c and e), 21–22 (beige in a–e), 17–19 (red in f–j), 13–16 (blue in f–j), 11–12 (green in f–j), 8–9 (velvet in k–o), 6 (dark blue in k–o), and 3–5 (dark yellow in k–o) months before the peak of El Niño, respectively. Vertical dotted lines indicate the month in which the respective forecasts are started. Observations are in black

Fig. 10

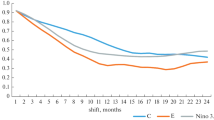
a Retrospective forecast of the EN3.4 time series in the period 1983–2014. The EN3.4 observation is in red and the model prediction at 6 months lead time is in blue. Scatterplots of the EN3.4 time series observation against forecast at b 3, c 6, d 18 months lead time. The respective regression coefficients are 0.70, 0.45 and 0.30