Abstract
We quantify the feedbacks from the physical climate system on the radiative forcing for idealized climate simulations using four different methods. The results differ between the methods and differences are largest for the cloud feedback. The spatial and temporal variability of each feedback is used to estimate the averaging scale necessary to satisfy the feedback concept of one constant global mean value. We find that the year-to-year variability, combined with the methodological differences, in estimates of the feedback strength from a single model is comparable to the model-to-model spread in feedback strength of the CMIP3 ensemble. The strongest spatial and temporal variability is in the short-wave component of the cloud feedback. In our simulations, where many sources of natural variability are neglected, long-term averages are necessary to get reliable feedback estimates. Considering the large natural variability and relatively small forcing present in the real world, as compared to the forcing imposed by doubling CO2 concentrations in the simulations, implies that using observations to constrain feedbacks is a challenging task and requires reliable long-term measurements.
Similar content being viewed by others
1 Introduction
Climate models still give a wide range of surface temperature responses to the same idealized external forcing, for example a doubling of the atmospheric CO2 concentration (Solomon et al. 2007). Most of these differences arise from physical processes, which are usefully conceptualized as feedbacks and can be isolated through a feedback analysis (Cess et al. 1990; Colman 2003; Soden and Held 2006). A variety of methods have been developed to isolate specific feedback mechanisms in climate models, raising the question as to how sensitive the results of such an analysis are to the methods employed.
The climate system is often described as being in equilibrium Footnote 1 if the global mean surface temperature, T s, does not change (\(\frac{\Updelta T_{\rm s}}{\Updelta t} = 0\)) and the net radiation at the top-of-the-atmosphere, R, is zero when averaged sufficiently long. If an external forcing, F, is imposed, for example through a change in greenhouse gas concentrations, the radiative budget at ToA departs from zero, and the system can be described as out of balance, or in disequilibirum. The climate system responds by changing the global mean surface temperature. This leads to increased energy being radiated back into space, so that the system can return to equilibrium. (The response of the system whereby increasing temperatures leads to increased outgoing radiation, is sometimes called the “Planck” feedback). The change in temperature affects other temperature-dependent climate processes. If those processes in turn have an effect on the radiation budget (and hence on temperature), they are referred to as climate “feedbacks”, analogously to the feedback definition in electronic circuits. Those feedbacks can have amplifying (positive feedback) and dampening (negative feedback) effects on the initial perturbation of the ToA radiation budget. This feedback concept is summarized in Eq. 1, where the feedback parameter λ (in units of Wm−2K−1) includes all physical feedback processes plus their mutual interactions. \(\Updelta T_{\rm s}\) is the change in global mean surface temperature. For a forcing from a doubling of the atmospheric CO2 concentration, the equilibrium temperature change is often referred to as the equilibrium climate sensitivity.
Physical feedbacks can be linked to quantities that change in response to a change in global mean surface temperature. The relevant physical quantities we will focus on in this study are the temperature, water vapor, surface albedo in snow and ice regions, and clouds. Other feedbacks, for instance due to biogeochemical processes are not considered here (e.g., Friedlingstein et al. 2006).
The feedback factor λ can be formally defined as
with
where x denotes individual feedback variables. The second-order term and all higher-order terms represent the interactions among different feedbacks. In a linear approximation, which may be considered valid for doubled CO2 conditions and the associated temperature changes (Boer and Yu 2003), these interactions are neglected.
Four physical feedback processes are considered. The total physical feedback factor λ can be separated, under the assumption of linearity, into a temperature (λT), water vapor (λWV), surface albedo (λA) and a cloud (λC) component:
The temperature feedback contribution (λT) to the total feedback can be further separated into a contribution by the Planck response λPL, or a homogeneous change in temperature, and a contribution by the change in the tropospheric temperature lapse rate λLR, which measures the rate at which temperature decreases with height (λT = λPL + λLR). The Planck response is the most fundamental feedback, characterized by the temperature dependence of the long-wave (LW) emission, where the emitted energy is proportional to the fourth power of the temperature, σT 4 (σ being the Stefan-Boltzmann constant). It is also sometimes referred to as the “no feedback” response.
The linearization in Eq. 2 is useful to disaggregate contributions of individual processes to the overall feedback and to estimate their relative importance. The quantification of individual feedbacks then allows one to compare models and quantify how various processes contribute to the overall uncertainty, as measured by the differences in the climate sensitivity across models (e.g., Bony and Dufresne 2005; Bony et al. 2006).
All processes in the climate system change in concert when the climate is changing, as measured by the change in global mean surface temperature. Different methods can be utilized to break down λ into the different contributions, all having in common that forcing and response are separated. How parts of the contributions are separated into forcing or response depends on the framework that is adopted. For instance, whether one adopts relative humidity or absolute humidity as a thermodynamic coordinate has a bearing on what will be identified as a feedback (Held et al. 2012).
Distinctions between feedbacks can also be arbitrary if different physical feedbacks are related to the same processes. For example, the water vapor feedback and the tropospheric temperature lapse rate feedback are anti-correlated. In models for which the lapse rate feedback is strongly negative (i.e., the lapse rate is reduced, leading to a decrease in the greenhouse effect), the water vapor feedback is strongly positive. The reason is that both feedbacks are related to the same mechanism, which is a change in deep convection. A weaker temperature lapse rate is generated by a greater warming at high altitudes than at the surface due to heat transport by convection. At the same time, enhanced convection also leads to more upper tropospheric water vapor (e.g., Cess 1975; Held and Soden 2000). For this reason, these two feedbacks are often added together and considered as a single feedback (λWV+LR), in which they partly compensate each other. By this the inter-model spread in the strength of this combined feedback is reduced. Huybers (2010) reports further compensations between different feedbacks (especially surface albedo and cloud feedback), but argues that those relations can in fact be an artifact due to, the methods used to estimate the feedbacks, the representation of physical relationships in the models, or how the models are conditioned on some combination of observations and expectations.
The concept of feedbacks, forcing and climate sensitivity has proved to be helpful in the idealized model world, but extrapolation to the real world has proven to be complicated. Partial derivatives can hardly be derived from observations, due to many interfering processes that are difficult to separate and to isolate from the background variability. But even in a model it can be difficult to isolate processes and estimate feedbacks, and as a result different methods have been developed to estimate the strength of feedbacks within models. And the question arises as to what extent estimates of feedback strength depend on methodological details.
Although the feedback parameters are defined in Eq. 2 are intensive properties of the climate system, they are often estimated locally, in space and time. By estimating these properties by averaging over local properties the question arises as to how well such intensive properties are sampled. Insufficient sampling, for instance over time periods that are small compared to the timescales of internal fluctuations within the climate system, may lead to biased estimates of feedback strengths. A feedback estimated for a certain year may be very different in other years and may depend on the nature of the fluctuations, so that the necessary averaging time may be different for different physical processes. The largest problem arises for clouds, which are highly variable in space and time, and tend to fluctuate strongly in association with other internal fluctuations within the climate system. This has implications for quantifying feedbacks from climate models and for deriving feedback factors from observations, or finding observational constraints.
The aim of this study is to compare and assess different methods for quantifying the strength of specific feedbacks, and to analyze the spatiotemporal variability that arise in the local contribution to the estimates of the overall feedback. To do so, we use climate model simulations with the atmospheric general circulation model ECHAM5 (Roeckner et al. 2003), coupled to a mixed-layer ocean. This idealized framework neglects factors contributing to natural variability such as volcanic eruptions, El Niño variability and varying modes of ocean circulations as well as less well defined contributions to the forcing such as from anthropogentic aerosols, or land use change.
In Sect. 2 we review the different methods to quantify feedbacks, and in Sect. 3 we describe the experimental set-up for the idealized climate change simulations. In Sect. 4 we analyze the different feedbacks, and discuss their geographical and temporal variability in Sect. 5 using the different methods. These results have implications for estimating feedback factors in the climate system from observations, which is discussed in the conclusions, Sect. 6.
2 Methods to quantify feedbacks in GCMs
Four different methods to estimate climate feedbacks have been proposed in the literature. They are based on two different principles. In this section we briefly describe these four methods. The first two methods are centered around a quantification of the sensitivity of radiative fluxes to perturbations from specific changes in the climate system, the second two methods are developed around diagnosed differences in the all-sky and clear-sky radiative fluxes. The first principle, of recomputing radiative fluxes for changed states, is less ambiguous, but involves performing radiative transfer computations and special model diagnostics (the kernel method helps to obviate this, by approximating the partial radiative perturbation method, without the need for repeated radiative transfer calculations on ancillary data). The second principle, of using changes in radiative fluxes from freely evolving runs, is only applicable to the cloud component of the feedback parameter, but as climate models differ mostly in the cloud feedback component, this approach is often used to estimate the radiative impact of changed clouds in a perturbed climate.
2.1 Partial radiative perturbation
This technique was first introduced by Wetherald and Manabe (1988) and more recently applied to an ensemble of atmosphere-ocean general circulation models by Colman (2003) and Soden and Held (2006). Offline radiative transfer calculations are used to estimate the effect of single variables such as temperature, water vapor, surface albedo or clouds on the ToA radiation. Under the assumption of linearity and separability each variable is substituted separately, one at a time, from a perturbed simulation, while all other radiation relevant variables are taken from a control simulation. This allows one to calculate each feedback factor separately for any variable x, as follows.
where Δx and \(\Updelta T_{\rm s}\) are obtained from the difference between a perturbed and a control simulation, and \(\Updelta_x R/\Updelta x\) is from off-line radiation calculations. In this equation, R again is the top-of-atmosphere net radiation flux, \(\Updelta T_{\rm s}\) is the surface temperature change, both spatially and temporally resolved, and Δx the three-dimensional, time-resolved change in quantity x. In the radiation calculation all other fields are taken from the control simulation, with x replaced by the field from the perturbed simulation. Specifically for the lapse-rate feedback, the differences in temperature changes within the troposphere (surface to tropopause) are applied as perturbation. For the cloud feedback, both changes in cloud fraction and cloud condensate mixing ratio are used. The Planck response (spatially uniform temperature change), water vapor feedback (change in water vapor mixing ratio) and surface albedo feedback (change in surface albedo) are straight forward to implement.
With this method the partial derivatives are calculated directly and it is closest to the formal definition of the feedback factor as defined in Eq. 2, with a few caveats. These caveats, can be thought of as assumptions that rise from a practical implementation of the method and are that: interactions between feedbacks are neglected, the climate change signal in any variable is the total derivative of variable x with temperature instead of the partial derivative, and the difference between perturbed and control simulations might not be small enough to allow for the discrete approximation of the derivative by the differentiation.
Colman and McAvaney (1997), Schneider et al. (1999) and Soden et al. (2004) pointed out that the assumption that all fields are uncorrelated introduces biases. Unintended perturbations are introduced to the radiation by de-correlating variables, but this can be partially overcome by applying this method twice. Once forward (FW), by substituting a variable from the perturbed climate (ptr) into the control climate (ctl) (∂ptr−ctl R x ) and once backward (BW) by taking a variable from the control climate and substituting it into the perturbed climate (∂ctl−ptr R x ). The final radiative perturbation is then better approximated by the average of these two estimates, \(\frac{\partial_{\rm ptr-ctl} R_{x} - \partial_{\rm ctl-ptr} R_{x}} {2}. \)
Because the partial radiative perturbation (PRP) method is more complex to implement than the other methods, spurious differences may arise when utilizing different radiative transfer codes for different models, depending on the exact implementation. It is also computationally expensive and needs special instantaneous model output. Most importantly, the radiative transfer part of the climate model needs to be isolated for the off-line radiative transfer computations.
2.2 Radiative kernels
The kernel method, introduced by Soden et al. (2008), is similar to the partial radiative perturbation (PRP) method, except that instead of recomputing the radiative fluxes for a given change in the state of the system, these fluxes are estimated from a linearization of the radiative transfer calculation. Instead of perturbing one variable at a time by an increment defined from a perturbed and a control simulation, as described above for the PRP method, the mean climate state is perturbed incrementally in the radiative flux computations level by level for each variable at a time by a pre-defined small unit increment, and the changes to the ToA radiation balance are computed as a “radiative kernel” for variable x (K x ) as a function of latitude, longitude, model level and time. The kernel for each variable x represents first fraction of formula 5 and is multiplied with the climate change signal from a forced simulation to calculate λ x . In contrast to the PRP, where offline radiation calculations are applied to every output step of the model, the kernels are applied as monthly averages, while the climate change signal still varies with the model output frequency. The advantage is that once those kernels are computed, offline radiation calculations are no longer necessary.
The temperature kernel (K T) is computed by perturbing the temperature at every level at each time by an increment of 1 K, while the specific humidity kernel (K W) is calculated by perturbing the specific humidity by an amount corresponding to about a 1 − K warming at fixed relative humidity. The 3-D surface albedo kernel is computed by perturbing the surface albedo fields by a 1 % increment (Soden et al. 2008).
A radiative kernel for clouds cannot be computed because radiation responds very non-linearly to cloud changes, and cloud changes themselves cannot be assumed to be small relative to the pre-existing cloudiness. However, it is possible to estimate the cloud feedback by splitting Eq. 2 into clear-sky and all-sky components and defining clear-sky feedback factors from clear-sky kernels (K 0x ) and full-sky kernels (K x). The change between perturbed and control climate of the the difference between full-sky and clear-sky situations yields for the right-hand-side of Eq. 2 the change in cloud radiative forcing, Δ CRF (see next section). This approach requires the definition of clear-sky kernels for the temperature, water vapor and surface albedo feedbacks, as well as the stratospheric adjusted radiative forcing (G) and clear-sky stratospheric adjusted radiative forcing (G 0).
2.3 Change in cloud radiative forcing
This method is most commonly used and easiest to apply, but is only applicable to the cloud feedback contribution to the total climate feedback parameter. It makes use of diagnostic variables that are commonly calculated on-line in climate simulations (Cess and Potter 1987). Clear-sky radiative fluxes are calculated (subscript clr), by setting the radiation-relevant cloud-related variables (cloud water- and cloud ice mixing ratios, as well as cloud fraction) to zero for a second diagnostic radiation call. This is done for the short-wave (SW) and long-wave (LW) components separately. The difference between the full-sky radiative flux calculations and the diagnostic clear-sky calculations yields the cloud radiative forcing (CRF), where the sum of the SW and LW component is the net cloud radiative forcing.Footnote 2
The difference of CRF between a perturbed climate (\(\Updelta \hbox{CRF}_{\rm prt}\)) and a control climate (\(\Updelta \hbox{CRF}_{\rm ctl}\)) defines the change in cloud radiative forcing (ΔCRF).
This quantity is often used as a proxy for the cloud feedback.
The ΔCRF method is widely used, because it gives an uncomplicated first estimate of the cloud influence on the radiation budget, and is especially helpful when assessing relative differences between climate models. Also, the cloud radiative forcing in the present-day climate is directly comparable with satellite observations (e.g. the Clouds and the Earth’s Radiant Energy System, CERES, Wielicki et al. 1996) in contrast to the offline calculated derivatives from the PRP and kernel method. Although comparisons with observations merit caution, because the clear-sky radiative fluxes with models are often computed differently than they are observed (Sohn et al. 2006).
The difficulty with this method lies in the components—all-sky and clear-sky radiation fluxes—being very large, on the order of hundreds of Wm−2, and still the the CRF in either the control and perturbed climate still on the order of tens Wm−2 (net CRF of about −20 Wm−2, Loeb et al. 2009), but the resulting ΔCRF is close to zero. Furthermore, the clear-sky components of the perturbed climate include contributions from the temperature lapse rate, water vapor and surface albedo feedback, which does not allow for an accurate separation of the cloud feedback from these other feedbacks. Some part of the change in cloud radiative forcing does thus not result from changes in cloud properties, but from a change in cloud masking, so that the ΔCRF does not accurately reflect the cloud feedback (Zhang et al. 1994; Colman 2003; Soden et al. 2004). It is often negative, even though the actual cloud feedback is generally slightly positive if diagnosed by the PRP method (and thus presumably more accurately in terms of the definition in Eq. 2) in climate models. However, when compared across models, the differences in the cloud radiative forcing predominantly arise from changes in the clouds.
2.4 Linear regression of TOA radiative flux imbalance versus surface temperature change
Gregory et al. (2004) proposed this method for use with simulations in which a forcing is instantaneously introduced, and then held constant over longer time periods (of the order of years to decades). It makes use of the relationship of the change in global-mean surface temperature (\(\Updelta T_{\rm s}\)) and the forcing (ΔF), which is expressed as the energy balance at the top-of-atmosphere (ΔR) where \(\Updelta\hbox{R}(\hbox{t})\) and \(\Updelta T_{\rm s}\) are now considered time dependent.
The variations of \(\Updelta R(t)\) and \(\Updelta T_{\rm s}(t)\) with time are regressed against each other as long term averages (e.g. yearly averages). Usually the global mean quantities are considered. This yields a regression line with a slope, −α, and an intercept, ΔF. The regression can be separated into the short- and long-wave components of R and F, and—analogous to the ΔCRF calculations above—also for clear- and cloudy skies, respectively. The regression slope −α for the cloudy-sky analysis is proportional to the cloud feedback estimate through the ΔCRF calculations. If regressed for the net full-sky radiative ToA imbalance, the regression slope is an estimate for the total feedback factor. The use of clear-sky fluxes is identical to ΔCRF so this method is facing the same interpretational issues.
The \(\Updelta T_{\rm s}\) intercept is equal to F α−1 which is the equilibrium \(\Updelta T_{\rm s}, \) or climate sensitivity if the applied forcing is a doubling of atmospheric carbon dioxide concentrations over pre-industrial levels. ΔR is approximately equal to the combined radiative forcing due to the fast adjustments in the troposphere and the stratospheric temperature adjustment, for \(\Updelta T_{\rm s} \to 0\) (see also Fig. 2). The advantage of this method is that forcing, cloud feedbacks and climate sensitivity can be estimated with the use of only a few years of model integration, without a need for any further diagnostics.
The regression method disaggregates forcing and response by assuming that they act on different time scales. This is different from the traditional separation of diagnosing a radiative forcing and considering the entire adjustment of the climate system as response Hansen et al. (1984). For example, clouds instantaneously respond to the increased CO2 concentrations, due to changes in the heating rate profiles and subsequently fast changes in atmospheric static stability, which is independent from the response to changes in surface temperature (Gregory and Webb 2008). This is referred to as a “ultrafast response” (Held et al. 2010) or, in analogy to aerosol indirect effects, as the “indirect CO2 effect” (Stevens and Schwartz 2012), or “semi-direct CO2 effect” (Andrews and Forster 2008). In the regression method the fast responses are best interpreted as adjustments which correct the forcing, although they would be interpreted as part of the feedback in the other methods. Compared to other methods, the regression method formalizes the forcing as the change in radiative fluxes that cannot be attributed to changes in globally averaged surface temperature, and in practice these are identified through the assumption that adjustments are fast compared to the timescale of surface temperature changes. In the following, we will refer to this regression method as the “Gregory-method”.
3 Model and experimental set-up
All feedback metrics are applied to the same set of simulations, using ECHAM5.4 (Roeckner et al. 2003), with a relatively coarse spectral resolution of T31 (approximately 3.75° resolution) and 19 vertical levels. First, a 20 years control integration is conducted with prescribed present-day greenhouse gas concentrations and with prescribed monthly varying sea-surface temperatures and sea-ice cover maps. The heat fluxes from this control simulation are used for the mixed-layer ocean integrations, with a 50 m mixed-layer ocean. ECHAM coupled to the mixed layer ocean is then integrated for a 20 years control integration and a 50 years integration with doubled CO2 concentrations, at which time a new equilibrium is reached. For our analysis the last 6 years of the control and the perturbed simulations are used. For all four applied methods, the same six hourly model output is used. The radiation code of ECHAM5.4, with 16 long-wave and 6 short-wave bands (Cagnazzo et al. 2007), is isolated from the model and used for the offline calculations for the radiative perturbation method and for computing the radiative kernels. For the calculations of the radiative kernels, incremental perturbations are applied to output fields of temperature, specific humidity and surface albedo from the control simulation.
For a quantification of the lapse rate feedback diagnostics of the tropopause height are necessary to exclude the stratospheric temperature change. Here we use the WMO defined tropopause of the control simulation which is saved together with the other instantaneous model output every 6 h.
By using the same model output and radiation code throughout this study we strive to be as consistent as possible. Differences in the results should thus only depend on the method used and its underlying assumptions.
4 Feedback factors
Global-, long-term averages (6 years) of the physical feedback factors analyzed using the different methods described in Sect. 2 are shown in Fig. 1. The error bars indicate the sampling error over the 6 years to give an estimate of the accuracy of the mean estimate given the limited sample used here. The boxes indicate ±1 standard error of single year averages, while the whiskers indicate the maximum and minimum value in a single year. Table 1 gives further details of the LW and SW contributions separately. The cloud feedback factor, λC, is calculated with four different methods, while for the tropospheric temperature lapse rate, water vapor and surface albedo feedbacks only the PRP and the radiative kernel methods are applicable. For the PRP method the forward (FW) calculated and the backward (BW) calculated feedback factor along with the average values are provided.
Surface albedo (λA), cloud (λC), water vapor (λWV), tropospheric temperature lapse rate (λLR) and the combined λWV and λLR feedback factors calculated with different methods. FW PRP: “Forward" PRP applying the control climate and the perturbed quantity from the climate change simulation, BW PRP: “Backward" PRP using the perturbed climate and the perturbed quantity from the control climate. PRP combined is the average of FW PRP and BW PRP. Each box is the 6-year mean feedback strength ± one standard error over the six annual averages. The whiskers indicate the maximum and minimum yearly averaged feedback strength of the six analyzed years. For the Gregory method the whiskers are calculated taking the maximum and minimum deviation from the regression, while the box gives the standard regression error. The pink shaded area indicates the range of feedback strength in CMIP3 models as published in Soden and Held (2006) for comparison
The Planck response is the strongest negative feedback with −3.23 to −3.08 Wm−2K−1, depending on the method (see Table 1). These three estimates of the Planck response are within the range of uncertainty as obtained from the year-to-year variability. The tropospheric temperature lapse rate feedback, λLR, is negative on a global, long-term average. This feedback differs the most depending on whether the FW or BW PRP is used, indicating non-linearities and strongest perturbations by de-correlating the different variables in the radiative flux calculations. The radiative kernel estimate is comparable to the FW PRP, but much larger in absolute terms than the BW PRP. The estimates of λLR obtained with the two different methods do not overlap within the standard error of the year-to-year variability, if the FW and BW calculated PRP are combined to a lapse rate feedback of −0.42 Wm−2K−1.
The water vapor feedback, λWV is the strongest positive feedback. For the water vapor feedback, the PRP and kernel method differ the most in an absolute sense. The water vapor feedback estimates derived with the PRP and kernel method do not agree within sampling error of the year-to-year variability. This is mainly due to the large differences in the LW component of this feedback. This feedback acts in both the SW and the LW spectra, but is dominated by the LW contribution that is responsible for ∼75 % of the total water vapor feedback. For the LW contribution the water vapor feedback factor differs strongly, depending on the method chosen.
Potential issues can arise through radiative artifacts around the tropopause as we do not account for the change in tropopause height in the offline radiation calculation. The tropopause height increases in the climate change simulations through the expansion of the troposphere. Substituting the water vapor fields from double CO2 climate in the control climate can lead to high water vapor concentrations in the lower stratosphere. Also the state dependence of the water vapor kernel (Jonko et al. 2012), which we computed only on the control climate, can lead to inconsistencies between feedback estimates through changes in cloud masking.
The sum of the water vapor and lapse rate feedbacks, λWV+LR, partly compensates the discrepancies between the PRP and kernel methods. The offsetting effect between those two feedback also leads to error compensation (see also Fig. 3) in the combined feedback. The LW components do not overlap within the standard error of the inter-annual variability for either λLR or λWV between the two methods, but they do in the combined feedback. This is analogous to the feedback strength difference for λLR and λWV among climate models, which decreases when the two are combined (Colman 2003, see also Fig. 1). This does not necessarily mean that models consistently simulate those feedbacks, but that errors are related and can compensate.
The surface albedo feedback is only affecting the SW radiation. In our simulations it is the smallest feedback, with 0.22/0.16 Wm−2K−1 using the PRP method and 0.17 Wm−2K−1, if calculated with the surface albedo kernel. These measures agree within the measure of uncertainty used here, when the PRP-FW and PRP-BW are combined, yielding a λA of 0.18 Wm−2K−1.
The cloud feedback affects the LW and SW radiation strongly, but the globally temporally averaged feedback factors are small. While the PRP method and kernel method give a positive cloud feedback the ΔCRF and Gregory-method give the opposite sign. This is expected, as ΔCRF and the Gregory-feedback are defined differently, and do not correspond directly to λC as defined in Eq. 2 (see Sect. 2). These differences arise from the cloud masking effect in the ΔCRF calculation, as well as in the Gregory method (see also Sect. 2). Despite not being consistent with the formally defined feedback framework, those two methods have both advantages, in terms of the practicality.
Figure 2 shows ΔCRF in relation to the change in surface temperature. The slopes of the regression lines for the cloud LW and cloud SW components indicate the cloud feedbacks. It is notable that both regression lines have a non-zero intercept at the Y-axis, and thus are interpreted as an adjustment to the forcing rather than a feedback (Gregory and Webb 2008). The regression error is used as the sampling error, comparable to the standard error of the inter-annual variability and the maximum and minimum distance from the regression line are used for the whiskers in Fig. 1. The uncertainties inferred from this are large, especially for the SW component.
The cloud feedback given by the Gregory-method would be the same as ΔCRF, if the regression line would be drawn between the zero intercept of the X- and Y-axis and the cloud of points on the right-hand side of Fig. 2 when the perturbed climate reached a new steady state. The fast adjustments of clouds, independent of the changes in the surface temperature, are considered part of the forcing and explain the difference. The net cloud feedback in Fig. 1 is similar to ΔCRF, as the fast adjustments (the Y-intercept) partly compensates in the SW and LW component (see Fig. 2). The fast adjustment is making the SW component of ΔCRF less positive and the LW component less negative, which is consistent with results from the CMIP3 ensemble (Andrews and Forster 2008).
The instantaneous CO2 adjustment in the LW component of the CO2 radiative forcing is larger in clear-skies than cloudy skies, because optically thick clouds will mask the effect on the outgoing long-wave radiation of the underlying CO2 changes. This effect (G − G0) contributes −0.55 Wm−2 for the model version used here.
5 Feedback variability
Feedback factors as they are customarily defined, are intensive properties of the climate system, and can in principal be estimated given sufficient sampling. When they are estimated using a global model that spatially and temporally resolves the climate system they can also be estimated locally, in which case the feedback factor can be interpreted as the average of feedback factors defined locally. Estimated in this way, as is usually the case, the question arises as to whether the sampling that underpins the estimate of the global feedback is sufficient. As for practical reasons feedback analyses are applied to relatively short periods which can be too short, as compared to the timescale of internal variability within the system, resulting in sampling errors when estimating feedbacks. The length of the averaging period depends on the feedback of interest and the tolerable error. In a climate model many sources of variability can be eliminated to minimize sampling requirements and to make the understanding of the feedback processes easier. For the experiments used here, we use a low resolution climate model (see Sect. 3), coupled to a mixed layer ocean. Due to this simplification the contribution of internal variability to sampling error is minimized, nonetheless an analysis of how spatial and temporal variability contribute to uncertainty in the estimation of the feedback factor provides insight into how a particular feedback functions, and a likely lower bound on estimates of sampling uncertainty. In the following we analyze spatial and temporal variability separately. As already mentioned, this variability is minimized by our experimental design, which does not incorporate a full dynamical ocean, interactive vegetation, sources of variability like volcanoes, or a varying solar constant. These additional factors are compounded by measurement uncertainty, a smaller and evolving forcing, and the shortness of the time-record when considering the natural system, rather than just more complex simulations, and is why observing feedback systems is so challenging.
5.1 Spatial variability
The geographical distributions of the surface albedo, water vapor, cloud and lapse rate feedback factors are shown in Fig. 4. Qualitatively the regional patterns of feedbacks do not differ among methods, hence we only show the geographical distributions calculated with the PRP method.
The Planck response (not shown) is the first order feedback, and represents the effect of a uniform change in temperature of the system in response to a forcing. It is strongly negative everywhere with −3.08 to −3.23 Wm−2K−1 as a global average, depending on the method (Table 1). As temperature rises with increasing carbon dioxide concentrations, the forcing gets balanced at the ToA through increased thermal radiation to space. The strongly non-linear relation (∼T 4) makes the Planck response strongest in the tropics, where temperatures are already high, and weakest in high latitudes, assuming a uniform temperature change.
The surface albedo feedback is only appreciably in mid to high latitudes (Fig. 4a) and mostly positive. Higher temperatures under doubled CO2 conditions cause less ice and snow to form in winter and lead to an earlier snow and ice melting in spring. The snow melt period contributes more potently to the feedbacks, because a phase lag with respect to the solar cycle means that variability in snowmelt occurs later in the spring than does snowfall in the autumn. Although locally this feedback factor can exceed 3 Wm−2K−1 (1 Wm−2K−1 on zonal average) and reaches its maximum in our simulations around 70−80° in both hemispheres, its strength, 0.17−0.22 Wm−2K−1 is small compared to the other feedbacks.
The water vapor feedback is strongly positive everywhere (Figs. 3, 4b) and geographical structures shows no systematic dependence on how it is calculated. The cold tropical tropopause and the dry subtropical subsiding branches of the upper atmosphere are most susceptible to changes in humidity, which leads to a maximum of λWV at about 15° N.
The lapse rate feedback (λLR, Figs. 3, 4d) is positive over large regions in the mid and high latitudes, mainly continental areas. At low latitudes, the atmosphere warms more at higher altitudes than at the surface, where the vertical temperature profile remains close to the moist adiabat due to the influence of deep convection. In mid- to high-latitude continental areas the surface temperature responds more strongly. A larger temperature response at the surface than aloft leads to a positive lapse rate feedback. Here the tropospheric temperature lapse rate is mainly controlled by baroclinic adjustment (Stone and Carlson 1979). For the temperature lapse rate feedback the difference is largest between the forward and backward calculated feedback factor (Fig. 1). The local contribution to the lapse rate feedback shows a sensitivity to the forward versus backward PRP estimate. These differences are strongest at high latitudes where the lapse rate feedback is positive, and result in a qualitative shift in the overall distribution of local contributions to the feedback factor (not shown). In these regions artificial perturbations are most relevant through de-correlation of the fields in the PRP method. Also changes in cloud masking strongly influence the results obtained when the PRP method is applied only one way (i.e, only FW).
5.1.1 Spatial variability of the cloud feedback
The local contribution to the global mean cloud feedback (Figs. 4c, 5) can be strongly negative or positive. On a global average this nearly cancels out, so that the global averaged feedback factor is close to zero (see Fig. 1; Table 1) and depending on the method, this average feedback can be positive or negative Footnote 3 are consistent with the estimates of the other methods. This makes the accurate estimation of the cloud feedback particularly difficult. Clouds can change their height, depth, size, frequency of occurrence, reflectivity, phase, or any combination of these. The cloud feedback thus affects the long- and short-wave spectra and is highly variable in space and time.
The geographical distributions of the net cloud feedback obtained from the PRP (Fig. 4c), kernels and ΔCRF (Fig. 5) look similar, but on a global average ΔCRF is lower, in our case in fact of a different (negative) sign. This is due to the temperature and water vapor feedbacks in the clear-sky component. Some parts of those feedbacks are not separated from the cloud feedback when subtracting the clear-sky component, if the cloud masking changes (see Sect. 2). Nonetheless, the zonally averaged structure is similar among the three methods, with a negative cloud feedback in the inner tropics, positive cloud feedback in the mid latitudes and again a negative feedback in the high latitudes. The cloud feedback maps differ in their detail but the corrected ΔCRF through the kernel method agrees better in its geographical distribution, as well in its global average, with the cloud feedback calculated using the PRP method.
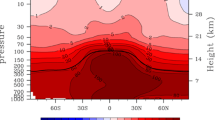
The bulk of the geographical variability comes from the short-wave component of the cloud feedback, which shows structures similar to the net cloud feedback (Fig. 7). Changes in the SW CRF are mainly due to changes in cloud cover (rather than cloud top height or cloud water content).
The LW component of the cloud feedback is globally positive except over subtropical oceans and polar regions, where it is slightly negative (Fig. 7). In our simulations the tropopause rises with increased warming, as the water vapor emission remains effective through a deeper layer. This leads to an upward shift of the profile of tropospheric infrared cooling. This decoupling of LW emission at the top of high anvil clouds from the surface emissions was described by Hartmann and Larson (2002) and Zelinka and Hartmann (2010), who hypothesized that through these mechanisms all global climate models simulate a positive LW cloud feedback.
The year-to-year variability in clouds is strong. If the PRP method is applied to 2 years of the same climate state, e.g. by taking cloud fields from 1 year and calculating their radiative perturbation as they are set in the atmospheric state of a different year, the radiative forcing can be of comparable magnitude to the cloud feedback (Fig. 6). In this—arbitrarily chosen—case the global mean ToA radiative forcing is −0.55 Wm−2, but over several years this averages out to zero. The main feature that gives confidence in the feedback in Figs. 4c and 5 is its structure, which is independent of the applied method. Especially the zonal structure appears robust. Little structure can be identified in the year-to-year variation of the cloud forcing, which indicates that the cloud-climate feedback can be separated from the natural variability in cloudiness.
Geographical distribution of cloud short-wave and cloud long-wave radiative feedback factor (left) and six hourly globally averages (right) of the components of cloud feedback factor for 6 years (grey lines), calculated using the FW PRP method. The red line in the time series is the 5 month running mean and the horizontal black lines is the mean over the entire time series. Note that the Y-axis range of the short-wave is the same as the range for the net cloud feedback factor and the range for the long-wave component is identical to all other feedback factors in Fig. 8
5.2 Temporal variability
The climate feedback concepts are estimated by globally and temporally averaging local contributions. Like the geographic variations, the temporal variations in the local contribution to the feedback factor also contain valuable information. Especially, if the goal is to assess feedback strength estimates from models using observations, or to infer feedback strength directly from observations, the variability characteristics become important if only as the background noise out of which a signal needs to be extracted. Figure 8 shows the temporal variability of the different feedbacks as global averages, every 6 h for six consecutive years, as calculated with the PRP method. The standard deviations in Table 1 are calculated from different yearly averages along each time series.
Time series of physical feedback factors for six hourly (grey line) globally averaged values for 6 years, calculated using the FW PRP method. The 5 months running mean (red line) is plotted to accentuated long term variability and the mean value (horizontal black line) is plotted as reference. Note the eight times larger range on the Y-axis of the cloud feedback factor
The time series in Fig. 8 for the globally averaged surface albedo-, lapse rate- and water vapor feedbacks show seasonality and vary within 0.5−1.0 Wm−2K−1 over the 6 years analyzed here. The variation in the lapse rate feedback and the water vapor are weakly anti-correlated on short (6 h) time-scales (correlation coefficient r = −0.21), but strongly correlated (r = 0.71) when averaged over 3 months. A weak lapse rate feedback is caused by a smaller temperature change aloft, leading to a small water vapor feedback at the same time. Huybers (2010) reports further correlation between feedbacks across climate models, which might not be entirely physical. We find that the surface albedo feedback and the lapse rate feedbacks have the strongest correlation (r = 0.31) on short time-scales (probably due to their common geographical structure, 4), even stronger than the correlation of the tropospheric temperature lapse rate with the water vapor feedback. On longer time-scales however, the correlation is only r = 0.5 related to the seasonal cycle. The global mean values of the net cloud feedback are correlated with the lapse rate feedback (r = 0.17 on short time scales and up to r = 0.31 on the time-scale of days) and a correlation between surface albedo and water vapor feedback also exists (up to 0.5 depending on the averaging time scale). All other combinations show little to no correlation.
Seasonally specific, but globally averaged, contributions to the surface albedo, lapse rate and water vapor feedback all show systematic variants. This is especially true for the surface albedo feedback, which is strongest in northern hemisphere spring when solar radiation at high northern latitudes starts to increase.
5.2.1 Temporal variability of the cloud feedback
The local contributions to the cloud feedback are much more variable than they are for the other feedbacks, but show no distinct seasonal variation in their global mean. Similarly to the the geographical distribution of the local contribution to the feedback strength, Fig. 4 in which strong positive or negative signals are evident locally, the global average of the local contributions to the cloud feedback factor also varies on the 6-hourly time scale by ±5 Wm−2K−1, although the time-averaged value remains close to zero.
The largest part of the temporal variability comes from the SW component of the cloud feedback (Fig. 7). This is dominated by contributions from changes in low clouds, which have a high albedo. Due to their low thermal contrast with the surface, the impact on the LW is much smaller, and its variability is comparable to the other feedbacks.
6 Implications and conclusions
By using different methods to separate physical feedbacks in idealized climate simulations, through a consistent use of model output and radiation code, we can explore methodological artifacts on estimates of feedback parameters. The largest differences arise simply from different definitions of forcing and feedback. Assumptions as to how processes are disaggregated introduces further differences among methods commonly used to diagnose feedbacks. Finally, the complexity of applying the PRP and Kernel methods can add further artificial contributions to the feedback signal, which are related to the specific diagnostic set up.
Overall the geographical distribution of the local contributions to a feedback factor are comparable among the methods, with robust regional features (although details differ). For the cloud feedback the geographical structure is consistent between years, giving confidence in the simulated feedback.
We also show that local processes that contribute to a feedback vary on different timescales and with a different magnitude, even if many modes of variability are excluded in our experiments. This makes long-term averages necessary for stable estimates of feedback factors. The cloud feedback varies the most in our simulations, especially in the SW spectrum, thereby introducing large sampling errors (on the order of magnitude of the actual feedback) if only short global temporal averages are used. In our simulations a single year is sufficient to estimate the surface albedo feedback, taking into account the year to year variability in Fig. 1. The tropospheric temperature lapse rate feedback requires about 3 years averaging time, although absolute differences are also large depending on the method. For the water vapor feedback this is about 5 years and for the cloud feedback all years need to be considered to obtain an accurate feedback estimate and might possibly not be sufficient in many cases, considering our very idealized experiments. For the latter, the sampling error of single years, combined with the methodological differences, can be as large as the inter-model difference in the CMIP3 ensemble (Fig. 1) and might be even larger in more complex models, let alone in reality.
Depending on one’s interest, even simple estimates of the ΔCRF can give valuable and reliable information, for example about the zonal structure of the cloud feedback. For the PRP and the kernel method, where all contributions to λ are known, Eq. 1 can be evaluated for a climate in equilibrium. This would verify whether all assumptions are justified when disaggregating local contributions to the feedback strength.
The forcing introduced by the doubling of the atmospheric CO2 concentration, as done in the perturbed simulation, can be calculated online as the stratospheric adjusted radiative forcing (see Stuber et al. 2001). This yields 3.89 Wm−2 for the model configuration used here. The forcing could also be estimated by using a CO2 kernel, analog to the other kernels for the feedback calculations, or taken from the Gregory method (3.91 Wm−2 in our case). The equilibrium climate sensitivity for the model configuration used here is 2.98 K.
For the PRP method Eq. 1, with the feedback parameter expanded as in Eq. 4, and with the radiation imbalance on the right-hand-side set to zero assuming an equilibrium is attained, yields:
For the radiative kernel method, it yields:
In both equations the residual is appreciably different from zero. Sampling errors, assumptions in the feedback diagnostic methodologies and specifics of how those methodologies are applied can lead to an inconsistency between feedbacks, forcing and climate response terms, which can exceed single feedback contributions.
Notes
Although customary, this language is somewhat unfortunate as the Earth system is a forced, and hence non-equilibrium, system. The state of constant temperature and zero net radiative imbalance is thus more precisely described as a system in stationarity.
Negative radiative fluxes are defined here as energy loss for the climate system, while positive radiative fluxes are an energy gain for the climate system.
Although it has been recognized that the CRF gives an estimate of the feedback that, because of masking effects, is biased low. Differences in sign of the cloud feedback for different regions.
References
Andrews T, Forster PM (2008) CO2 forcing induces semi-direct effects with consequences for climate feedback interpretation, Geophys Res Lett 35:L04802. doi:10.1029/2007GL032273
Boer GJ, Yu B (2003) Climate sensitivity and climate state. Clim Dyn 21:167–176
Bony S, Dufresne J (2005) Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models. Geophys Res Lett 32:L20806. doi:10.1029/2005GL023851
Bony S et al (2006) How well do we understand and evaluate climate change feedback processes? J Clim 19:3445–3482
Cagnazzo C, Manzini E, Giorgetta MA, De F, Fortster PM, Morcrette JJ (2007) Impact of an improved shortwave radiation scheme in the MAECHAM5 general circulation model. Atmos Chem Phys 7:2503-2515
Cess R (1975) Global climate change: an investigation of atmospheric feedback mechanisms. Tellus 27:193–198
Cess RD, Potter GL (1987) Exploratory studies of cloud radiative forcing with a general circulation model. Tellus A 39A(5):460–473. doi:10.1111/j.1600-0870.1987.tb00321.x
Cess RD et al (1990) Intercomparison and interpretation of climate feedback processes in 19 atmospheric general circulation models. J Geophys Res 95:16601–16615
Colman RA, McAvaney BJ (1997) A study of general circulation model climate feedbacks determined from perturbed sea surface temperature experiments. J Geophys Res 102(D16):19383–19402. doi:10.1029/97JD00206
Colman R (2003) A comparison of climate feedbacks in GCMs. Clim Dyn 20:865–873
Friedlingstein P et al (2006) Climate-carbon cycle feedback analysis: results from the C4MIP model intercomparison. J Clim 19:3337–3353. doi:10.1175/JCLI3800.1
Gregory JM, Ingram WJ, Palmer MA, Jones GS, Stott PA, Thorpe RB, Lowe JA, Johns TC, Williams KD (2004) A new method for diagnosing radiative forcing and climate sensitivity. Geophys Res Lett 31:L03205
Gregory J, Webb M (2008) Tropospheric adjustment induces a cloud component in CO2 forcing. J Clim 21(1):58–71. doi:10.1175/2007JCLI1834.1
Hansen J, Lacis A, Rind D, Russell G, Stone P, Fung I (1984) Climate sensitivity: analysis of feedback mechanisms, climate processes and climate sensitivity, geophysical monograph 29, American Geophysical Union, pp 130–163
Hartmann DL, Larson K (2002) An important constraint on tropical cloud-climate feedback. Geophys Res Lett 29(20). doi:10.1029/2002GL015835
Held I, Soden B (2000) Water vapor feedback and global warming. Annu Rev Energy Environ 25:441–475. doi:10.1146/annurev.energy.25.1.441
Held IM, Winton M, Takahashi K, Delworth T, Zeng F, Vallis G (2010) Probing the fast and slow components of global warming by returning abruply to preindustrial forcing. J Clim 23:2418–2427
Held IM, Shell KM (2012) Using relative humidity as a state variable in climate feedback analysis. J Clim 25:2578–2582
Huybers P (2010) Compensation between model feedbacks and curtailment of climate sensitivity. J Clim 23:3009–3018. doi:10.1175/2010JCLI3380.1
Jonko A, Shell K, Sanderson B, Danabasoglu G (2012) Climate feedbacks in CCSM3 under changing CO2 forcing. part i: adapting the linear radiative kernel technique to feedback calculations for a broad range of forcings. J Clim doi:10.1175/JCLI-D-11-00524.1
Loeb NG, Wielicki BA, Doelling DR, Smith GL, Keyes DF, Kato S, Manalo-Smith N, Wong T (2009) Toward optimal closure of the earth’s top-of-atmosphere radiation budget. J Clim 22:748–766. doi:10.1175/2008JCLI2637.1
Roeckner E et al (2003) The atmospheric general circulation model ECHAM5. Part I: model description, Tech. Rep. 349, Max-Planck-Institut für Meteorologie, Hamburg, Germany
Schneider EK, Kirtman BP, Lindzen RS (1999) Tropospheric water vapor and climate sensitivity. J Atmos Sci 56:1649–1658
Soden BJ, Broccoli AJ, Hemler RS (2004) On the use of cloud forcing to estimate cloud feedback. J Clim 17:3661–3665
Soden BJ, Held IM (2006) An assessment of climate feedbacks in coupled ocean-atmoshere models. J Clim 19:3354–3360
Soden BJ, Held IM, Colman R, Shell KM, Kiehl JT, Shields CA (2008) Quantifying climate feedbacks using radiative kernels. J Clim 21(14):3504–3520
Sohn B-J, Schmetz J, Stuhlmann R, Lee J-Y (2006) Dry bias in satellite-derived clear-sky water vapor and its contribution to longwave cloud radiative forcing. J Clim 19:5570–5580
Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt K, Tignor M, Miller H (2007) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Stevens B, Schwartz SE (2012) Observing and modeling earth’s energy flows. Surv Geophy 33(3–4):779–816
Stone Peter H, Carlson John H (1979) Atmospheric lapse rate regimes and their parameterization. J Atmos Sci 36:415–423
Stuber N, Sausen R, Ponater M (2001) Stratosphere adjusted radiative forcing calculations in a comprehensive climate model. Theor Appl Climatol 68(3):125–135
Wetherald RT, Manabe S (1988) Cloud feedback processes in a general circulation model. J Atmos Sci 45:1397–1416
Wielicki Bruce A, Barkstrom Bruce R, Harrison Edwin F, Lee Robert B, Smith G Louis, Cooper John E (1996) Clouds and the Earth’s radiant energy system (CERES): an earth observing system experiment. Bull Am Meteorl Soc 77:853–868
Zelinka MD, Hartmann DL (2010) Why is longwave cloud feedback positive? J Geophys Res 115:D16117. doi:10.1029/2010JD013817
Zhang MH, Hack JJ, Kiehl JT, Cess RD (1994) Diagnostic study of climate feedback processes in atmospheric general circulation models. J Geophys Res 99(D3):5525–5537. doi:10.1029/93JD03523
Acknowledgments
We thank the Max Planck Society, the International Max Planck Research School for Earth System Modeling and the German Research Foundations Emmy Noether grant for supporting this work. We also thank two anonymous reviewers for their constructive comments on the initial manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Klocke, D., Quaas, J. & Stevens, B. Assessment of different metrics for physical climate feedbacks. Clim Dyn 41, 1173–1185 (2013). https://doi.org/10.1007/s00382-013-1757-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1757-1