Arranging Solid Balls to Represent a Graph

Abstract.

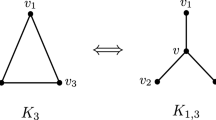
 By solid balls, we mean a set of balls in R ³ no two of which can penetrate each other. Every finite graph G can be represented by arranging solid balls in the following way: Put red balls in R ³, one for each vertex of G, and connect two red balls by a chain when they correspond to a pair of adjacent vertices of G, where a chain means a finite sequence of blue solid balls in which each consecutive balls are tangent. (We may omit the chain if the two red balls are already tangent.) The ball number b(G) of G is the minimum number of balls (red and blue) necessary to represent G. If we put the balls and chains on a table so that all balls sit on the table, then the minimum number of balls for G is denoted by b _T (G). Among other things, we prove that b(K ₆)=8,b(K ₇)=13 and b _T (K ₅)=8,b _T (K ₆)=14. We also prove that c ₁ n ³<b(K _n )<c ₂ n ³ log n, c ₃ n ⁴ log n<b _T (K _n )<c ₄ n ⁴.