Chvátal–Erdös Type Conditions for Hamiltonicity of Claw-Free Graphs

Abstract

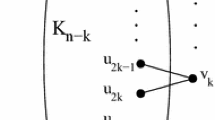
For a graph H, let $\alpha (H)$ and $\alpha ^{\prime }(H)$ denote the independence number and the matching number, respectively. Let $k\ge 2$ and $r>0$ be given integers. We prove that if H is a k-connected claw-free graph with $\alpha (H)\le r$, then either H is Hamiltonian or the Ryjá c̆ ek’s closure $cl(H)=L(G)$ where G can be contracted to a k-edge-connected $K_3$-free graph $G_0^{\prime }$ with $\alpha ^{\prime }(G_0^{\prime })\le r$ and $|V(G_0^{\prime })|\le \max \{3r-5, 2r+1\}$ if $k\ge 3$ or $|V(G_0^{\prime })|\le \max \{4r-5, 2r+1\}$ if $k=2$ and $G_0^{\prime }$ does not have a dominating closed trail containing all the vertices that are obtained by contracting nontrivial subgraphs. As corollaries, we prove the following:

• (a) A 2-connected claw-free graph H with $\alpha (H)\le 3$ is either Hamiltonian or $cl(H)=L(G)$ where G is obtained from $K_{2,3}$ by adding at least one pendant edge on each degree 2 vertex;

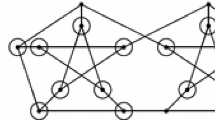
• (b) A 3-connected claw-free graph H with $\alpha (H)\le 7$ is either Hamiltonian or $cl(H)=L(G)$ where G is a graph with $\alpha ^{\prime }(G)=7$ that is obtained from the Petersen graph P by adding some pendant edges or subdividing some edges of P.

Case (a) was first proved by Xu et al. [19]. Case (b) is an improvement of a result proved by Flandrin and Li [12]. For a given integer $r>0$, the number of graphs of order at most $\max \{4r-5, 2r+1\}$ is fixed. The main result implies that improvements to case (a) or (b) by increasing the value of r and by enlarging the collection of exceptional graphs can be obtained with the help of a computer. Similar results involved degree or neighborhood conditions are also discussed.