1 Introduction

There exist numerous methods for the analysis and visualization of multi-fields. One particular approach is the comparison of scalar fields via topological descriptors. The understanding, interpretation, and computation of topological descriptors remain a challenging task [30]. One of these tools is the Jacobi set. The Jacobi set is based on Morse theory and captures gradient alignments among multiple scalar fields. Currently, Jacobi set computation is based on piecewise linear approximations on triangulations [8]. Piecewise linear interpolation typically produces non-smooth and inaccurate results. In the case of edge-based Jacobi set extraction, it leads to zig-zag patterns and discretization artifacts as illustrated in the top row of Fig. 1. These zig-zag patterns are even preserved for higher resolutions since the traditional method only extracts the edges of the underlying triangulation and does not utilize the cell interior. To address these problems, previous works explore the simplifications of Jacobi sets by either simplifying the scalar functions (indirect methods) or the extracted Jacobi sets (direct methods). While these approaches may improve the Jacobi set representation, they all rely on extracting edges that form the Jacobi set using a piecewise linear approach.

Fig. 1
figure 1

Comparison of the traditional piecewise linear method (top) and our local bilinear method (bottom) for a fixed resolution and different zoom levels on a rectangular grid. The Jacobi set is marked in black and the color-coding corresponds to the ground-truth gradient alignment field (of two analytic functions). The color bar is ordered from positive (top) to negative (bottom), where white indicates the zero. It can be observed that the piecewise linear method results in zig-zag patterns and discretization artifacts, whereas our method leads to a smoother representation of the Jacobi set

Full size image

In this paper, our main goal is to extend the piecewise linear computation to a bilinear one to arrive at a more accurate geometry of the extracted Jacobi set. To achieve this, we introduce an equivalent formulation of the piecewise linear method and then extend it to our higher-order approach. Our contributions can be summarized as follows:

  • We provide an equivalent formulation for the computation of Jacobi sets and embed the piecewise linear method into this framework.

  • Due to the reformulation, we introduce a novel Jacobi set extraction that depends on bilinear interpolation, leading to a smoother, non-edge-based Jacobi set representation.

  • We present an efficient local subdivision method that further improves the extracted Jacobi set representation.

We compare our method to the piecewise linear method for three different datasets: an analytic dataset, a dataset with a von Kármán vortex street, and the Hurricane Isabel dataset.

The paper is structured as follows: After the introduction, we review related work in Sect. 2. To lay the foundations, Sect. 3 provides the theoretical background of Jacobi sets as well as the piecewise linear method to calculate them. In Sect. 4, we introduce the relevant concepts for our local bilinear approach. Subsequently, we derive our approach in three steps and present an efficient local subdivision scheme. Next, Sect. 5 provides a thorough evaluation of our method. Finally, the conclusion with future research directions is presented in Sect. 6.

2 Related work

The context of this paper is the analysis and visualization of multi-fields via the comparison of scalar fields. In the following, we will summarize previous works that address this topic by extracting joint topological structures [17, 30], some of which are closely related to the notion of Jacobi sets

Simultaneous analysis of isosurfaces of several scalar fields using a variation density function has been proposed by Nagaraj et al. [23]. Tools studying multivariate data topologically go one step further. Such methods are, in particular, the piecewise linear computation of Jacobi set [8], the Reeb space [11] and its variants [6], Pareto sets [19], and multivariate persistent homology [5]. The Reeb space compresses the components of the level sets of a multivariate mapping and obtains a summary representation of their relationships. Instead of exploring Jacobi sets in the domain, Chattopadhyay et al. [7] studied multi-field topology by considering projections of the Jacobi set into the Reeb space. Thus, these two concepts are shown to be related as the image of the Jacobi sets under the mapping corresponds to certain singularities in the Reeb space [6].

Another related concept is that of Pareto sets [19]. Here, a set of scalar fields is analyzed with respect to consensus or disagreement among ascending and descending manifolds, critical points, and their connectivity. A follow-up paper [18] investigates the relation to Jacobi sets and derives subset and equivalence relations between Jacobi sets and Pareto sets. In addition, the mapper construction [28] and the joint contour nets [6] can be considered as discrete variants of the Reeb space.

All these previous works either introduce a different topological descriptor or establish connections to the concept of Jacobi sets. In contrast, our approach aims to improve the geometrical representation of Jacobi sets with a higher-order interpolation scheme.

As part of topological data analysis tools, the Jacobi set can be used to compare multiple scalar fields [10], track critical points [4, 8], define silhouettes of objects [12], and extract ridges in image analysis [26]. It has also been employed in various scientific applications [1, 2, 8, 20, 22]. However, in practice, the Jacobi set contains degeneracies and discretization artifacts that can be reduced by simplification of the Jacobi set. Bremer et al. [4] perform persistent simplification of the scalar field to remove small loops of the Jacobi set that lie entirely within successive time steps. Luo et al. [21] compute the Jacobi set by approximating the gradients of a pair of scalar fields. Nagaraj and Natarajan [24] simplify the Jacobi set by explicitly reducing the number of components. Bhatia et al. [3] identify and remove unimportant portions of the Jacobi set by determining how the pair of scalar fields must be modified locally. Our proposed work utilizes bilinear interpolation to obtain a smoother and more accurate geometric representation of the Jacobi set (compared to the piecewise linear approach), while preserving its topology. Therefore, our work can be seen as a completely different approach. To the best of our knowledge, the computation of Jacobi sets under higher-order interpolation schemes has not been explored and understood, and our investigation using bilinear interpolation is the first step in this direction.

Another related concept is the general search for parallel vectors in two fields, e.g., for the computation of ridgelines or the detection of vortex cores in the flow. An introduction to the parallel vectors operator has been given by Peikert and Roth [27], formulated as a search for roots of the cross-product of the two vector fields. As a computational solution, they suggest an extraction via zero-level isolines for two-dimensional vector fields, e.g., by using marching squares. Further improvements for higher-dimensional fields were presented by Theisel et al. [29] and van Gelder et al. [14], who express the problem as a streamline integration problem and make use of tracing algorithms.

While our approach also works with cross-products and an extraction via zero-level isolines, we focus on an edge-based identification of gradient alignments. To be more precise, our Jacobi set extraction starts with scalar fields, computes edge-based gradients in a local bilinear fashion, and identifies the gradient alignments. This means that we do not extract a global gradient field, which is necessary for the parallel vectors operator. Furthermore, due to the preservation of the topology of the piecewise linear method [8], our approach guarantees several topological properties; in particular, it satisfies the Even Degree Lemma [8], which is at the core of our connection method.

3 Background

In this section, we review the underlying theory of Jacobi sets and outline the piecewise linear computation of Jacobi sets by Edelsbrunner and Harer [8].

3.1 Jacobi sets and Morse theory

The Jacobi set is defined for a pair of Morse functions on a smooth d-manifold \({{\mathbb M}}\). For the purpose of this paper, we restrict our attention to a subset \({{\mathbb M}}\subset \mathbb {R}^2\) of the Euclidean space \(\mathbb {R}^2\). Given a smooth function \(f :{{\mathbb M}}\rightarrow {{\mathbb R}}\), the gradient \(\nabla f({\mathbf {x}})\) at the point \({\mathbf {x}}\in {{\mathbb M}}\) is well-defined by its partial derivatives. The point \({\mathbf {x}}\) is a critical point if the gradient vanishes; otherwise it is a regular point. A critical point \({\mathbf {x}}\) is non-degenerate if the Hessian (i.e., the matrix of second-order derivatives) is invertible. The function f is a Morse function if every critical point is non-degenerate and the critical points have distinct function values [9, page 128].

Given two Morse functions \(f, g :{{\mathbb M}}\rightarrow {{\mathbb R}}\), the Jacobi set \({{\mathbb J}}(f,g)\) is defined as the set of points where the gradients of both functions are linearly dependent [8], that is

$$\begin{aligned} {{\mathbb J}}(f,g):=&\{{\mathbf {x}}\in {{\mathbb M}}\mid \nabla f({\mathbf {x}}) + \lambda \nabla g({\mathbf {x}}) = 0 \\&\qquad \text { or } \lambda \nabla f({\mathbf {x}}) + \nabla g({\mathbf {x}}) = 0, \, \lambda \in {{\mathbb R}}\}\\ =&\{{\mathbf {x}}\in {{\mathbb M}}\mid {\mathbf {x}}\text { is a critical point of } f({\mathbf {x}}) + \lambda g({\mathbf {x}})\\&\qquad \text { or of } \lambda f({\mathbf {x}}) + g({\mathbf {x}}), \, \lambda \in {{\mathbb R}}\}. \end{aligned}$$

In other words, points in the Jacobi set are referred to as the simultaneous critical points of f and g [8]. For any value \(t \in {{\mathbb R}}\), we consider the restriction of f to the level sets \(g^{-1}(t)\) of g, \(f_t: g^{-1}(t) \rightarrow {{\mathbb R}}\). \({{\mathbb J}}(f,g)\) can be alternatively formulated as the closure of the set of critical points of \(f_t\), that is

$$\begin{aligned} {{\mathbb J}}(f,g)=&\text {cl}\{{\mathbf {x}}\in {{\mathbb M}}\mid {\mathbf {x}}\text { critical point of } f_t, \text { for some } t \in {{\mathbb R}}\}. \end{aligned}$$

The Jacobi set is symmetric, i.e., \({{\mathbb J}}(f,g)={{\mathbb J}}(g,f)\). Furthermore, it is a smoothly embedded 1-manifold in \({{\mathbb M}}\) [8].

3.2 Piecewise linear computation of Jacobi sets

We now describe the traditional piecewise linear computation of Jacobi sets following the work of Edelsbrunner and Harer [8]. Let K be a triangulation of \({{\mathbb M}}\) and let \(\phi , \psi :{\text {Vert}}(K) \rightarrow {{\mathbb R}}\) be functions defined on the vertices of K, \({\text {Vert}}(K)\). They consider the functions f and g to be the piecewise linear extensions of \(\phi \) and \(\psi \), respectively, \(f, \, g :|K| \rightarrow {{\mathbb R}}\). Then, they model both of these functions as the limits of a series of smooth functions, \(\lim _{n\rightarrow \infty } f_n = f\) and \(\lim _{n\rightarrow \infty } g_n = g\). The Jacobi set is constructed as the limit, \({{\mathbb J}}(f,g) := \lim _{n\rightarrow \infty } {{\mathbb J}}(f_n, g_n)\).

The computation of \({{\mathbb J}}(f,g)\) is performed by tracing the critical points of the 1-parameter family of functions \(h_{\lambda } = f+\lambda g\) along the edges of K. To be more precise, the algorithm determines for each edge \({{\mathbf {a}}{\mathbf {b}}}\) the value \(\lambda \), such that \(h_{\lambda }({\mathbf {a}}) = h_{\lambda } ({\mathbf {b}})\). This leads to \(\lambda =\lambda _{{{\mathbf {a}}{\mathbf {b}}}}=(f_{\mathbf {b}}-f_{\mathbf {a}})/(g_{\mathbf {a}}-g_{\mathbf {b}})\).

To determine whether such an edge \({{\mathbf {a}}{\mathbf {b}}}\) is critical (i.e., belonging to the Jacobi set), the algorithm examines the link of \({{\mathbf {a}}{\mathbf {b}}}\). Recall that the star of a simplex \(\tau \in K\) is the collection of simplices that contains \(\tau \); and the link includes simplices in the closure of the star, i.e., \({\text {St}}(\tau ) = \{\sigma \in K \mid \tau \le \sigma \}\) and \({\text {Lk}}(\tau ) = \{\nu \in {\text {Cl}}({\text {St}}(\tau )) \mid \nu \cap \tau = \emptyset \}\). The lower star of a vertex \({\mathbf {a}}\) consists of all simplices in the star that have \({\mathbf {a}}\) as their highest vertex, while the lower link is the portion of the link that bounds the lower star. The lower link of \({{\mathbf {a}}{\mathbf {b}}}\) is the subcomplex of vertices \(\mathbf {v}_i\) whose \(h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}\) function values are smaller than the ones from \(\mathbf {a}\) and \(\mathbf {b}\).

Let l be the restriction of \(h_{\lambda _{ab}}\) to the link of \({{\mathbf {a}}{\mathbf {b}}}\). The computation relies on the following lemma.

Critical Edge Lemma An edge \({{\mathbf {a}}{\mathbf {b}}}\) belongs to \({{\mathbb J}}\) if and only if vertex \({\mathbf {a}}\) is a critical point of l. Moreover, the multiplicity of \({{\mathbf {a}}{\mathbf {b}}}\) in \({{\mathbb J}}\) is the multiplicity of \({\mathbf {a}}\) as critical point of l.

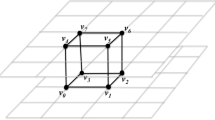
An edge \({{\mathbf {a}}{\mathbf {b}}}\) with the vertices \({\mathbf {v}_1}\) and \({\mathbf {v}_2}\) in its link \({\text {Lk}}({{\mathbf {a}}{\mathbf {b}}})\) (see Fig. 2) is a Jacobi edge or critical if and only if [25]

$$\begin{aligned} h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) \quad&\text {and} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})>h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2}) ,\end{aligned}$$
(1)
$$\begin{aligned} \text {or} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})< h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) \quad&\text {and} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})< h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2}). \end{aligned}$$
(2)

We differentiate between the criticality of the edges: if Eq. 1 holds, the edge is maximal; if Eq. 2 holds, the edge is minimal. These inequalities may lead to degenerate cases, which are resolved by using the Simulation of Simplicity [13]. We refer to Natarajan [25] for details.

Recall that the degree of a vertex is the number of edges that contain the vertex. After computing a set of critical edges, the next step of the algorithm is to construct the 1-manifold \({{\mathbb J}}\). Based on the Even Degree Lemma by Edelsbrunner and Harer [8], stated below, the algorithm concatenates the edges in pairs, thus forming the 1-manifold \({{\mathbb J}}\). Our proposed approach builds upon the above edge-based Jacobi set extraction under bilinear interpolation.

Even Degree Lemma The degree of a vertex in \({{\mathbb J}}\) is even.

Fig. 2
figure 2

Critical edge test for 2-dimensional complexes. The reverse transformation line from a quadratic \(\{{\mathbf {a}}{\mathbf {v}_1}{\mathbf {b}}{\mathbf {v}_2}\}\)-cell between \({\mathbf {v}_1}\) and \({\mathbf {v}_2}\) is marked by the dotted lines

Full size image

4 Our approach

In this section, we first outline the motivation for our approach by establishing a new perspective on the piecewise linear method. This lays the foundation for our proposed local bilinear method that preserves the topology of Jacobi set from [8] and extracts the Jacobi set locally with a bilinear interpolation scheme. Thus, the restriction to an edge-based Jacobi set representation is avoided and the geometry is enhanced. Finally, an appropriate local subdivision method for an efficient Jacobi set extraction is presented.

4.1 Motivation and derivation

The piecewise linear computation of Jacobi sets by Edelsbrunner and Harer [8] has several limitations. One of these is that only the edges of the underlying triangulation can be identified as components of the Jacobi set. This leads to zig-zag patterns, poor convergence for increasing mesh resolution, and an imprecise Jacobi set representation. To avoid these issues, the natural way is to use a higher-order interpolation scheme, which is the core of our approach.

To apply this, we propose to use an equivalent formulation of Jacobi sets, that is

$$\begin{aligned} {{\mathbb J}}(f,g)=\left\{ \mathbf {x}\in {{\mathbb M}}\mid \nabla f(\mathbf {x}) \times \nabla g(\mathbf {x}) = 0 \right\} . \end{aligned}$$
(3)

In our setting, where \({{\mathbb M}}\) is a smooth 2-manifold embedded in \({{\mathbb R}}^3\), the cross-product of \(\nabla f({\mathbf {x}})\) and \(\nabla g({\mathbf {x}})\) can be expressed with the help of the unit vectors \({\mathbf {e}}_i\) and the determinant

$$\begin{aligned} \nabla f({\mathbf {x}}) \times \nabla g({\mathbf {x}})=\det \begin{pmatrix} {\mathbf {e}}_1 &{} \partial _1 f({\mathbf {x}}) &{} \partial _1 g({\mathbf {x}})\\ {\mathbf {e}}_2&{}\partial _2 f({\mathbf {x}}) &{}\partial _2 g({\mathbf {x}}) \\ {\mathbf {e}}_3 &{} \partial _3 f({\mathbf {x}}) &{} \partial _3 g({\mathbf {x}}) \end{pmatrix}. \end{aligned}$$

Assuming that \({{\mathbb M}}\) lies in the xy-plane, the cross-product is

$$\begin{aligned} \nabla f({\mathbf {x}}) \times \nabla g({\mathbf {x}})= \left( \partial _{x} f({\mathbf {x}}) \partial _{y} g({\mathbf {x}}) - \partial _{y}f({\mathbf {x}}) \partial _{x} g({\mathbf {x}}) \right) \cdot \mathbf {e}_3. \end{aligned}$$

We define \(\kappa _{\mathbf {x}}\), called gradient alignment value, as

$$\begin{aligned} \kappa _{\mathbf {x}}(f,g):=\partial _{x} f({\mathbf {x}}) \partial _{y} g({\mathbf {x}}) - \partial _{y}f({\mathbf {x}}) \partial _{x} g({\mathbf {x}}). \end{aligned}$$
(4)

The gradient alignment value \(\kappa _{\mathbf {x}}\) characterizes the linear independence of the gradients at the point \({\mathbf {x}}\in {{\mathbb M}}\). This leads to the scalar field \(\kappa _{\mathbf {x}}: {{\mathbb M}}\rightarrow {{\mathbb R}}\) as a function of \({\mathbf {x}}\), which we call the gradient alignment field. According to the Jacobi set definition, the point \({\mathbf {x}}\) belongs to the Jacobi set \({{\mathbb J}}(f,g)\) if and only if \( \kappa _{\mathbf {x}}(f,g)=0\).

Fig. 3
figure 3

Illustration of the scalar field f over two connected triangles \({\mathbf {abv}_1}\) and \({\mathbf {av}_2\mathbf {b}}\)

Full size image

Our next step is to examine how the (smooth) gradient alignment field \(\kappa _{\mathbf {x}}(f,g)\) behaves for both linearly and bilinearly interpolated functions f and g, the corresponding gradient alignment fields are denoted \(\kappa _{\mathbf {x}}^{\mathrm {li}}\) and \(\kappa _{\mathbf {x}}^{\mathrm {bi}}\), respectively.

We assume f to be linear in each of the triangles \(\{{\mathbf {abv}_1}\}\) and \(\{{\mathbf {av}_2\mathbf {b}}\}\) (for the notation, see Fig. 3). For the triangle \(\{{\mathbf {abv}_1}\}\), we use the formula \(f_{{\mathbf {abv}_1}}(x,y):=a^f_{00} + a^f_{10}x + a^f_{01}y\), which leads to the following system of linear equations:

$$\begin{aligned} \begin{pmatrix} 1&{}x_{\mathbf {a}}&{}y_{{\mathbf {a}}} \\ 1&{}x_{\mathbf {b}}&{}y_{{\mathbf {b}}} \\ 1&{}x_{\mathbf {v}_1}&{}y_{{\mathbf {v}_1}}\\ \end{pmatrix}\cdot \begin{pmatrix} a_{00}^f\\ a_{10}^f\\ a_{01}^f \end{pmatrix} = \begin{pmatrix} f_{\mathbf {a}}\\ f_{\mathbf {b}}\\ f_{\mathbf {v}_1} \end{pmatrix}, \end{aligned}$$
(5)

where \(f_{\mathbf {a}}=f(x_{\mathbf {a}},y_{{\mathbf {a}}} )\), \(f_{\mathbf {b}}=f(x_{\mathbf {b}},y_{{\mathbf {b}}} )\), \(f_{\mathbf {v}_1}=f(x_{\mathbf {v}_1},y_{{\mathbf {v}_1}})\). The analytical solution leads to the following gradient of \(f_{{\mathbf {abv}_1}}\):

$$\begin{aligned}&\nabla f_{{\mathbf {abv}_1}}(x,y)=\begin{pmatrix} a_{10}^f\\ a_{01}^f \end{pmatrix} \\&=\frac{1}{A_{{\mathbf {abv}_1}}} \begin{pmatrix} (f_{\mathbf {b}}-f_{\mathbf {a}})y_{{\mathbf {v}_1}}+(f_{\mathbf {a}}-f_{\mathbf {v}_1})y_{{\mathbf {b}}} +(f_{\mathbf {v}_1}-f_{\mathbf {b}})y_{{\mathbf {a}}} \\ (f_{\mathbf {a}}-f_{\mathbf {b}})x_{\mathbf {v}_1}+(f_{\mathbf {v}_1}-f_{\mathbf {a}})x_{\mathbf {b}}+(f_{\mathbf {b}}-f_{\mathbf {v}_1})x_{\mathbf {a}} \end{pmatrix}, \end{aligned}$$

where \(A_{{\mathbf {abv}_1}} = x_{\mathbf {a}}(y_{{\mathbf {b}}} -y_{{\mathbf {v}_1}}) + x_{\mathbf {b}}(y_{{\mathbf {v}_1}}-y_{{\mathbf {a}}} ) + x_{\mathbf {v}_1}(y_{{\mathbf {a}}} -y_{{\mathbf {b}}} )\) describes the area of the parallelogram spanned by the edges \({\mathbf {v}_1}{\mathbf {a}}\) and \({\mathbf {v}_1}{\mathbf {b}}\). An analogous calculation can be done for \(f_{{\mathbf {av}_2\mathbf {b}}}\), \(g_{{\mathbf {abv}_1}}\), and \(g_{{\mathbf {av}_2\mathbf {b}}}\). According to Equation  4, the gradient alignment value at the vertex \({\mathbf {v}_1}\) is given by

$$\begin{aligned} \kappa _{{\mathbf {v}_1}}^{\mathrm {li}}(f,g)&=\nabla f_{{\mathbf {abv}_1}}({\mathbf {v}_1}) \times \nabla g_{{\mathbf {abv}_1}}({\mathbf {v}_1}) \nonumber \\&=\frac{ (f_{\mathbf {b}}-f_{\mathbf {a}})g_{\mathbf {v}_1}+ (f_{\mathbf {a}}-f_{\mathbf {v}_1})g_{\mathbf {b}}+ (f_{\mathbf {v}_1}-f_{\mathbf {b}})g_{\mathbf {a}}}{A_{{\mathbf {abv}_1}}}. \end{aligned}$$
(6)

Analogously, for the triangle \(\{{\mathbf {av}_2\mathbf {b}}\}\), we compute the gradient alignment value at the vertex \({\mathbf {v}_2}\) via

$$\begin{aligned} \kappa _{{\mathbf {v}_2}}^{\mathrm {li}}(f,g)&=(\nabla f_{{\mathbf {av}_2\mathbf {b}}}({\mathbf {v}_2}) \times \nabla g_{{\mathbf {av}_2\mathbf {b}}}({\mathbf {v}_2})) \nonumber \\&=\frac{(f_{\mathbf {a}}-f_{\mathbf {b}})g_{\mathbf {v}_2}+ (f_{\mathbf {v}_2}-f_{\mathbf {a}})g_{\mathbf {b}}+ (f_{\mathbf {b}}-f_{\mathbf {v}_2})g_{\mathbf {a}}}{A_{{\mathbf {av}_2\mathbf {b}}}}. \end{aligned}$$
(7)

These calculations show that the resulting values \(\kappa _{\mathbf {v}_1}^{\mathrm {li}}(f,g)\) and \(\kappa _{\mathbf {v}_2}^{\mathrm {li}}(f,g)\) stem from the gradient alignment field \(\kappa ^{\mathrm {li}}_{\mathbf {x}}\), that is constant on each triangle (because the gradients \(\nabla f\) and \(\nabla g\) are constant on each triangle). With these observations and the fact that the Jacobi set is equal to the zero-level set of \(\kappa _{\mathbf {x}}\), it is possible to identify critical edges via a change of sign with respect to \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}(f,g)\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}(f,g)\).

Fig. 4
figure 4

Overview of our local bilinear method with one subdivision step: critical edges (red), Jacobi set points (blue dots), the connected Jacobi set via line segments (blue), and resulting T-nodes (orange). After the detection of critical edges via edge-based (linear) gradient alignment values (a), the Jacobi set points are computed via (bilinear) gradient alignment values at locations indicated by the dotted lines (b). Then, the Jacobi set points are connected using the underlying connectivity of the critical edges (c). The last illustration shows the result after one subdivision step, including the resulting T-nodes (d)

Full size image

Comparing these considerations with the approach of Edelsbrunner and Harer [8], we will notice that the two approaches are equivalent. To show this, we consider an edge \({{\mathbf {a}}{\mathbf {b}}}\) with \({\text {Lk}}({{\mathbf {a}}{\mathbf {b}}})=\left\{ {\mathbf {v}_1},{\mathbf {v}_2}\right\} \). For the edge \({{\mathbf {a}}{\mathbf {b}}}\) to be critical, either Eq. 1 or Eq. 2 needs to be true. Let us assume that Eq. 1 holds. We can reformulate it in terms of \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\):

$$\begin{aligned}&\quad \,\,\,\,\, h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) \quad \text {and} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2})\\ \Leftrightarrow \quad&0> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) - h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}}) \quad \text {and} \quad 0> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2})- h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}}) \\ \Leftrightarrow \quad&0>\frac{(f_{\mathbf {b}}-f_{\mathbf {a}})g_{{\mathbf {v}_1}} + (f_{{\mathbf {a}}}-f_{{\mathbf {v}_1}})g_{\mathbf {b}}+ (f_{{\mathbf {v}_1}}-f_{{\mathbf {b}}})g_{\mathbf {a}}}{g_{\mathbf {a}}-g_{\mathbf {b}}}\\ \text {and} \quad&0<\frac{ (f_{\mathbf {a}}-f_{\mathbf {b}})g_{{\mathbf {v}_2}} + (f_{{\mathbf {v}_2}} - f_{{\mathbf {a}}})g_{\mathbf {b}}+ (f_{{\mathbf {b}}}-f_{{\mathbf {v}_2}})g_{\mathbf {a}}}{g_{\mathbf {a}}-g_{\mathbf {b}}}. \\ \Leftrightarrow \quad&0>\frac{\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\cdot A_{{\mathbf {a}},{\mathbf {b}},{\mathbf {v}_1}}}{g_{\mathbf {a}}-g_{\mathbf {b}}} \quad \text {and} \quad 0<\frac{\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\cdot A_{{\mathbf {a}},{\mathbf {v}_2},{\mathbf {b}}}}{g_{\mathbf {a}}-g_{\mathbf {b}}}. \end{aligned}$$

An analogous calculation can be done for Eq. 2 with swapped signs for both conditions. As a result, the following relations, which explicitly show the connection between the approach of Edelsbrunner and Harer and the gradient alignment field, can be established:

$$\begin{aligned}&\text {Eq{1}:}\quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) \quad \text {and} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})> h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2})\\&\Leftrightarrow \,\, {\left\{ \begin{array}{ll} \text {if } g_{\mathbf {a}}-g_{\mathbf {b}}> 0: \quad 0> \kappa ^{\mathrm {li}}_{{\mathbf {v}_1}}A_{{\mathbf {abv}_1}} \quad \text {and}\quad 0<\kappa ^{\mathrm {li}}_{{\mathbf {v}_2}}A_{{\mathbf {av}_2\mathbf {b}}}, \\ \text {if } g_{\mathbf {a}}-g_{\mathbf {b}}< 0: \quad 0< \kappa ^{\mathrm {li}}_{{\mathbf {v}_1}}A_{{\mathbf {abv}_1}} \quad \text {and}\quad 0>\kappa ^{\mathrm {li}}_{{\mathbf {v}_2}}A_{{\mathbf {av}_2\mathbf {b}}}, \end{array}\right. } \\&\text {Eq.{2}:}\quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})< h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_1}) \quad \text {and} \quad h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {a}})< h_{\lambda _{{{\mathbf {a}}{\mathbf {b}}}}}({\mathbf {v}_2})\\&\Leftrightarrow \,\, {\left\{ \begin{array}{ll} \text {if } g_{\mathbf {a}}-g_{\mathbf {b}}> 0: \quad 0< \kappa ^{\mathrm {li}}_{{\mathbf {v}_1}}A_{{\mathbf {abv}_1}} \quad \text {and}\quad 0>\kappa ^{\mathrm {li}}_{{\mathbf {v}_2}}A_{{\mathbf {av}_2\mathbf {b}}},\\ \text {if } g_{\mathbf {a}}-g_{\mathbf {b}}< 0: \quad 0 > \kappa ^{\mathrm {li}}_{{\mathbf {v}_1}}A_{{\mathbf {abv}_1}} \quad \text {and}\quad 0<\kappa ^{\mathrm {li}}_{{\mathbf {v}_2}}A_{{\mathbf {av}_2\mathbf {b}}}, \end{array}\right. } \end{aligned}$$

where the term \(g_{\mathbf {a}}- g_{\mathbf {b}}\) determines whether an edge \({{\mathbf {a}}{\mathbf {b}}}\) is maximal or minimal.

At this point, the consequences are twofold. Firstly, the gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}(f,g)\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}(f,g)\) characterize a new Jacobi set condition for the edge \({{\mathbf {a}}{\mathbf {b}}}\) via

$$\begin{aligned} {{\mathbf {a}}{\mathbf {b}}}\in {{\mathbb J}}(f,g) \, \Leftrightarrow \, {\text {sgn}}\big (\kappa ^{\mathrm {li}}_{{\mathbf {v}_1}}(f,g)\big ) \ne {\text {sgn}}\big (\kappa ^{\mathrm {li}}_{{\mathbf {v}_2}}(f,g)\big ). \end{aligned}$$
(8)

Secondly, we observe that the piecewise linear approach by Edelsbrunner and Harer is also equivalent to the condition in Eq. 8. In fact, the conditions only differ in a scaling factor: whereas the gradient alignment field for linearly interpolated functions f and g (on each triangle) encodes both the topology and geometry in the condition (due to the scaling \(A_{\mathbf {abv}_1}\) and \(A_{\mathbf {av}_2\mathbf {b}}\)), the approach by Edelsbrunner and Harer solely relies on topological relations.

Now, the next step is to investigate how the gradient alignment field \(\kappa _{\mathbf {x}}(f,g)\) behaves for bilinearly interpolated functions f and g. To this end, let f and g be given on the quadrilateral \(\{{\mathbf {a}}{\mathbf {v}_1}{\mathbf {b}}{\mathbf {v}_2}\}\)-cell (for the notation, see Fig. 3) by the coefficients \(b_{ij}^f\) and \(b_{ij}^g\), respectively, and the formula

$$\begin{aligned} f(x,y)&=b_{00}^f+b_{10}^f x+b_{01}^f y+b_{11}^f xy,\\ g(x,y)&=b_{00}^g+b_{10}^g x+b_{01}^g y+b_{11}^g xy. \end{aligned}$$

The coefficients can be analogously computed to Eq. 5 via a system of linear equations. However, in this case the gradients are not constant and are given by

$$\begin{aligned} \nabla f(x,y) = \begin{pmatrix} b_{10}^f+b_{11}^f y\\ b_{01}^f + b_{11}^f x \end{pmatrix}, \quad \nabla g(x,y) = \begin{pmatrix} b_{10}^g+b_{11}^g y\\ b_{01}^g + b_{11}^g x \end{pmatrix}. \end{aligned}$$

Hence, the gradient alignment field \(\kappa _{\mathbf {x}}\) is linear as the following general calculation shows:

$$\begin{aligned} \kappa _{\mathbf {x}}^{\mathrm {bi}}(f,g)&= \nabla f(x,y) \times \nabla g(x,y) \nonumber \\&= \left( b_{10}^f b_{01}^g - b_{01}^f b_{10}^g\right) + \left( b_{10}^f b_{11}^g - b_{11}^f b_{10}^g\right) x \nonumber \\&\quad + \left( b_{11}^f b_{01}^g - b_{01}^f b_{11}^g\right) y. \end{aligned}$$
(9)

This aspect enables the computation of the zero-level set in the quadrilateral, instead of identifying critical edges of the underlying triangulation. In fact, the method by Edelsbrunner and Harer can be extended using a bilinear interpolation scheme. To be more precise, the gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\) (see Eq. 6 and Eq. 7) are used for the topological identification of critical edges, whereas for the geometrical identification a bilinear interpolation scheme is used.

To this end, the gradient alignment values \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_2}\) in the case of bilinearly interpolated f and g are given by the following formulas (we skip the technical details):

$$\begin{aligned} \kappa ^{\mathrm {bi}}_{\mathbf {v}_1}&= \frac{1}{D} \cdot \Big ( A_{{\mathbf {abv}_1}} \cdot \kappa ^{\mathrm {li}}_{\mathbf {v}_1}\cdot \big (x_{\mathbf {v}_2}y_{{\mathbf {v}_1}} + x_{\mathbf {v}_1}y_{{\mathbf {v}_2}} - x_{\mathbf {v}_2}y_{{\mathbf {v}_2}} \big ) \nonumber \\&+ A_{{\mathbf {a}}{\mathbf {v}_2}{\mathbf {v}_1}}\cdot \kappa _a^{\mathrm {li}}\cdot \big ( x_{\mathbf {v}_1}y_{{\mathbf {b}}} + x_{\mathbf {b}}y_{{\mathbf {v}_1}} - x_{\mathbf {b}}y_{{\mathbf {b}}} \big ) + A_{{\mathbf {av}_2\mathbf {b}}} \cdot \kappa ^{\mathrm {li}}_{\mathbf {v}_2}\cdot \big ( x_{\mathbf {v}_1}y_{{\mathbf {v}_1}} \big ) \nonumber \\&+ A_{{\mathbf {b}}{\mathbf {v}_1}{\mathbf {v}_2}}\cdot \kappa _b^{\mathrm {li}}\cdot \big ( x_{\mathbf {v}_1}y_{{\mathbf {a}}} +x_{\mathbf {a}}y_{{\mathbf {v}_1}} -x_{\mathbf {a}}y_{{\mathbf {a}}} \big ) \Big ),\end{aligned}$$
(10)
$$\begin{aligned} \kappa ^{\mathrm {bi}}_{{\mathbf {v}_2}}&= \frac{-1}{D} \cdot \Big ( A_{{\mathbf {a}}{\mathbf {v}_2}{\mathbf {b}}} \cdot \kappa _{\mathbf {v}_2}^{\mathrm {li}}\cdot \big (x_{\mathbf {v}_1}y_{{\mathbf {v}_1}} - x_{\mathbf {v}_1}y_{{\mathbf {v}_2}} - x_{\mathbf {v}_2}y_{{\mathbf {v}_1}} \big ) \nonumber \\&+ A_{{\mathbf {a}}{\mathbf {v}_2}{\mathbf {v}_1}}\cdot \kappa _{\mathbf {a}}^{\mathrm {li}}\cdot \big (x_{\mathbf {b}}y_{{\mathbf {v}_2}} + x_{\mathbf {v}_2}y_{{\mathbf {b}}} - x_{\mathbf {b}}y_{{\mathbf {b}}} \big ) +A_{\mathbf {abv}_1}\cdot \kappa _{\mathbf {v}_1}^{\mathrm {li}}\cdot (x_{\mathbf {v}_2}y_{{\mathbf {v}_2}}) \nonumber \\&+ A_{{\mathbf {b}}{\mathbf {v}_1}{\mathbf {v}_2}}\cdot \kappa _b^{\mathrm {li}}\cdot \big (x_{\mathbf {a}}y_{{\mathbf {a}}} - x_{\mathbf {a}}y_{{\mathbf {v}_2}} - x_{\mathbf {v}_2}y_{{\mathbf {a}}} \big )\Big ). \end{aligned}$$
(11)

The values \(\kappa ^{\mathrm {li}}_{\mathbf {a}}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {b}}\) are given by

$$\begin{aligned} \kappa ^{\mathrm {li}}_a(f,g):= \frac{(f_{\mathbf {v}_1}- f_{\mathbf {v}_2})g_{\mathbf {a}}+ (f_{\mathbf {v}_2}- f_{\mathbf {a}})g_{\mathbf {v}_1}+ (f_{\mathbf {a}}-f_{\mathbf {v}_1})g_{\mathbf {v}_2}}{A_{{\mathbf {a}}{\mathbf {v}_2}{\mathbf {v}_1}}} \\ \kappa ^{\mathrm {li}}_b(f,g):= \frac{(f_{\mathbf {v}_2}- f_{\mathbf {v}_1})g_{\mathbf {b}}+ (f_{\mathbf {v}_1}-f_{\mathbf {b}})g_{\mathbf {v}_2}+ (f_{\mathbf {b}}-f_{\mathbf {v}_2})g_{\mathbf {v}_1}}{A_{{\mathbf {b}}{\mathbf {v}_1}{\mathbf {v}_2}}} \end{aligned}$$

with the area for counter-clockwise sorted \(\mathbf {p}_1\),\(\mathbf {p}_2\), and \(\mathbf {p}_3\):

$$\begin{aligned} A_{\mathbf {p}_1\mathbf {p}_2\mathbf {p}_3}&:= \det \begin{pmatrix} x_{\mathbf {p}_1} &{} x_{\mathbf {p}_2} &{} x_{\mathbf {p}_3}\\ y_{\mathbf {p}_1} &{} y_{\mathbf {p}_2} &{} y_{\mathbf {p}_3}\\ 1 &{} 1 &{}1 \end{pmatrix}\\&= x_{\mathbf {p}_1}(y_{\mathbf {p}_2}-y_{\mathbf {p}_3})+ x_{\mathbf {p}_2}(y_{\mathbf {p}_3}- y_{\mathbf {p}_1}) + x_{\mathbf {p}_3}(y_{\mathbf {p}_1} - y_{\mathbf {p}_2}). \end{aligned}$$

The denominator D is computed via

$$\begin{aligned} D&= \big ((x_{\mathbf {a}}-x_{\mathbf {v}_1})\cdot (x_{\mathbf {b}}- x_{\mathbf {v}_2}) \big ) \cdot \big (y_{\mathbf {a}}y_{\mathbf {v}_1}+ y_{\mathbf {b}}y_{\mathbf {v}_2}\big ) \\&+ \big ((x_{\mathbf {a}}-x_{\mathbf {b}})\cdot (x_{\mathbf {v}_2}-x_{\mathbf {v}_1}) \big )\cdot \big (y_{\mathbf {a}}y_{\mathbf {b}}+ y_{\mathbf {v}_1}y_{\mathbf {v}_2}\big ) \\&+\big ( (x_{\mathbf {a}}- x_{\mathbf {v}_2}) \cdot (x_{\mathbf {v}_1}-x_{\mathbf {b}}) \big ) \cdot \big (y_{\mathbf {a}}y_{\mathbf {v}_2}+ y_{\mathbf {b}}y_{\mathbf {v}_1}\big ). \end{aligned}$$

4.2 Algorithm

An overview of our local bilinear method is given in Fig. 4, and the algorithm can be divided into three steps:

  1. 1.

    Computation of linear gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {x}}\) with the identification of critical edges.

  2. 2.

    Computation of Jacobi set points via the bilinear gradient alignment values \(\kappa ^{\mathrm {bi}}_{\mathbf {x}}\).

  3. 3.

    Generation of the Jacobi set representation \({{\mathbb J}}(f,g)\).

4.2.1 Identification of critical edges

In the previous subsection, we formulated a method (compare Eq. 8), that is topologically equivalent to the one of Edelsbrunner and Harer [8] in terms of the (linear) gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\). We use these values to identify critical Jacobi set edges. This is the first part of our method and also the initial step in Algorithm 1. To be more precise, given edges \(E=(\mathbf {e}_i)\), we iterate over each edge \(\mathbf {e}_i\) (line 2), identify \({\mathbf {v}_1}\) and \({\mathbf {v}_2}\) as the lower link of \(\mathbf {e}_i\) (line 3), and compute the gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\) via Eq. 6 and Eq. 7 (line 4). Afterward, the critical edge test via the change of sign method is performed (line 5).

While the piecewise linear approach stops here (identifying critical edges of the underlying triangulation), the next step of our method is to determine a geometrically more precise Jacobi set representation via Jacobi set points.

figure g

4.2.2 Computation of Jacobi set points

In contrast to the piecewise linear computation by Edelsbrunner and Harer, we avoid marking critical edges of the underlying triangulation by introducing Jacobi set points. As illustrated in Fig. 4a, a Jacobi set point is conceptually assigned to a critical edge \({{\mathbf {a}}{\mathbf {b}}}\) and lies on the line segment that connects the vertices \({\mathbf {v}_1}\) and \({\mathbf {v}_2}\) via \({\mathbf {m}}\) (compare Fig. 2).

Given the fact that bilinearly interpolated functions f and g result in a linear gradient alignment field on the quadrilateral \(\{{\mathbf {a}}{\mathbf {v}_1}{\mathbf {b}}{\mathbf {v}_2}\}\)-cell, there is only one zero on this line segment if the signs of the values \(\kappa _{\mathbf {v}_1}\) and \(\kappa _{\mathbf {v}_2}\) differ. In this context, the zero of the line segment is given by

$$\begin{aligned} 0= \kappa _{{\mathbf {v}_1}}+\lambda \cdot (\kappa _{{\mathbf {v}_2}}-\kappa _{{\mathbf {v}_1}}) \quad \Leftrightarrow \quad \lambda = - \frac{\kappa _{{\mathbf {v}_1}}}{\kappa _{{\mathbf {v}_2}}-\kappa _{{\mathbf {v}_1}}}, \end{aligned}$$

where \(\lambda \) is the weighting coefficient that characterizes the location of the zero via

$$\begin{aligned} \mathbf {p}_i= {\left\{ \begin{array}{ll} {\mathbf {v}_1}+ 2\lambda \cdot ({\mathbf {m}}-{\mathbf {v}_1}) \qquad \quad \,\, \text {if } \lambda < 1/2, \\ {\mathbf {m}}+(1-2\lambda )\cdot ({\mathbf {m}}-{\mathbf {v}_2}) \quad \text {if }\lambda \ge 1/2. \end{array}\right. } \end{aligned}$$
(12)

Thus, the main idea is that the collection of all Jacobi set points approximates the Jacobi set (see Fig. 4b and c). The computation of Jacobi set points is the second part of Algorithm 1 (starting with a critical edge \(\mathbf {e}_i\) in line 6) and will be explained in the following in more detail.

To compute a Jacobi set point, we compute the bilinear gradient alignment values \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_2}\) (line 6). Then, we perform the change of sign method for \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_2}\) (line 7). In the case of different signs, the weighting coefficient \(\lambda \) characterizing the Jacobi set point is computed via bilinear gradient alignment values \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {bi}}_{\mathbf {v}_2}\) (line 8). Otherwise, linear gradient alignment values \(\kappa ^{\mathrm {li}}_{\mathbf {v}_1}\) and \(\kappa ^{\mathrm {li}}_{\mathbf {v}_2}\) are used (line 10). Finally the exact location of the Jacobi set point is computed via Eq. 12 (line 11–15) and added to the list of pairs \((\mathbf {e}_i, \mathbf {p}_i)\) of Jacobi set points \(\mathbf {p}_i\) and critical edges \(\mathbf {e}_i\) (line 16).

4.2.3 Connection of Jacobi set points

figure h

Given a collection of Jacobi set points computed by Algorithm 1, our goal is to connect them in a way such that they geometrically approximate the Jacobi set \({{\mathbb J}}(f,g)\). To achieve this, we utilize the preserved topological properties of the (linear) gradient alignment values (from Edelsbrunner and Harer, see Eq. 8) to apply the Even Degree Lemma. According to the lemma, the vertices \({\mathbf {a}}\) and \({\mathbf {b}}\) of a Jacobi edge \({{\mathbf {a}}{\mathbf {b}}}\) have an even degree. It implies that a Jacobi edge \({{\mathbf {a}}{\mathbf {b}}}\) is connected to an even number of other Jacobi edges. This is due to the fact that the degrees of \({\mathbf {a}}\) and \({\mathbf {b}}\) are even and since both degrees include the edge \({{\mathbf {a}}{\mathbf {b}}}\) as well, the number of Jacobi edges connected to \({{\mathbf {a}}{\mathbf {b}}}\) equals \((\text {degr}({\mathbf {a}})-1)+(\text {degr}({\mathbf {b}})-1)\). The important consequence of this is:

Each Jacobi set point is connected to an even number (greater than zero) of Jacobi set points and, in particular, there are no isolated Jacobi set points.

Based on this result, we can describe a method to connect Jacobi set points. An illustration of this method is presented in Fig. 5, and a detailed description is given by Algorithm 2, which will be explained in the following. Given the list of pairs \((\mathbf {e}_i, \mathbf {p}_i)\) of Jacobi set points \(\mathbf {p}_i\) that are related to critical edges \(\mathbf {e}_i\), we iterate over each critical edge \(\mathbf {e}_i\) (line 2) to find all critical edges \(\mathbf {e}_{i_j}\) that share a vertex with \(\mathbf {e}_i\) (line 3). These are used to construct line segments \(l=(\mathbf {p}_i, \mathbf {p}_j)\) with the respective Jacobi set points \(\mathbf {p}_i\) and \(\mathbf {p}_j\) (line 4-5). This method produces a collection of line segments that geometrically approximates the Jacobi set while preserving the topology.

Algorithm 2 could be considered as a “dualization” process where each critical edge is replaced by its corresponding Jacobi set point (as its “dual”); in fact, two Jacobi set points are connected by a line segment if their corresponding critical edges share the same vertex. This aspect is visualized in Fig. 5, where we use a color-coding and numbering to highlight the connectivity. In the top, the pairs of critical edges and Jacobi set points are represented (the dotted lines emphasize the pairs). The bottom image shows the Jacobi set representation with our connection method. The effect of our connection method is that the adjacency of critical edges (e.g., edge 1 is connected to the edges 0, 2, 3 and 5) is reflected by the connectivity of Jacobi set points (see the respective Jacobi sets points). In this way, the topology of the piecewise linear method is preserved. We provide a formal proof of the homotopy equivalence in Appendix.

Fig. 5
figure 5

Illustration of our connection method for the computed Jacobi set points. The top shows our computed Jacobi set points along with the piecewise linear method, and the bottom illustrates how our method connects the points. A protruding triangle (resulting in a loop) is shown on the left, whereas a straightforward topology is presented on the right

Full size image

4.3 Local subdivision method

One of the advantages of our local bilinear approach is the usage of a geometrically more precise extraction of the Jacobi set. This typically leads to better convergence properties compared to piecewise linear schemes. Therefore, we propose a local subdivision scheme that makes use of the already identified critical edges by only doing computations in these locations. Given a critical edge \(\mathbf {e}_i = {{\mathbf {a}}{\mathbf {b}}}\) and the related Jacobi set point \(\mathbf {p}_i\) within a \(\{{\mathbf {a}}{\mathbf {v}_1}{\mathbf {b}}{\mathbf {v}_2}\}\)-cell (see Fig. 6), we now describe a single subdivision step for the edge \({{\mathbf {a}}{\mathbf {b}}}\):

  • For the critical edge \({{\mathbf {a}}{\mathbf {b}}}\), bisect each edge that belongs to the two adjacent triangles and connect the new vertices \(\mathbf {x}_1, \ldots , \mathbf {x}_5\) such that 8 smaller triangles are obtained.

  • Use an interpolant to compute the function values of f and g at the new vertices \(\mathbf {x}_1, \ldots , \mathbf {x}_5\).

  • Our local bilinear method can now be applied to the resulting new edges \(\mathbf {e}_1, \ldots , \mathbf {e}_8\).

This procedure is done for each critical edge, which means a local efficient subdivision scheme is used. An illustration is presented in Fig. 4d. It can be observed that T-nodes occur, which violate the rules of a triangulation. However, for our purposes, we do not need a consistent global triangulation for further computations. The new critical edges and Jacobi set points will only be computed in the local neighborhood, and therefore, the T-nodes do not affect the repeated application of the local subdivision method.

Fig. 6
figure 6

Local refinement around a critical edge \({{\mathbf {a}}{\mathbf {b}}}\)

Full size image

5 Results

To evaluate our local bilinear method qualitatively and quantitatively, we apply it to three different datasets: an analytical example, a simulated von Kármán vortex street, and the multi-field Hurricane Isabel dataset. Additionally, it is compared to the piecewise linear method by Edelsbrunner and Harer [8]. The methods are performed using MATLAB (R2022a) on a MacBook Pro with an Intel Dual-Core i5 CPU @ 3.1 GHz and 8 GB of RAM. The computation times for each of the datasets are given in Table 1.

Table 1 Comparison of computation times (in seconds). For the piecewise linear method the time for identifying critical edges was measured. For the local bilinear method with and without subdivision (subd.) the computation times of Algorithm 1 and 2 were added
Full size table
Fig. 7
figure 7

Contour lines of the analytic functions f (red dashed lines) and g (blue dotted lines) with the resulting analytic Jacobi set \({{\mathbb J}}(f,g)\) marked in black

Full size image

For the quantitative analysis, we introduce the gradient alignment measure \(\mu \) that measures the accuracy of the extracted Jacobi set. Given a globally computed gradient alignment field \(\kappa _{\mathbf {x}}(f,g)\) as well as a Jacobi set representation \(JS=\{l_k = (\mathbf {p}_{k_i},\mathbf {p}_{k_j})\}\) via a collection of line segments, we define the gradient alignment measure as

$$\begin{aligned} \mu (JS) :&= \frac{ \int _{JS} \kappa _{\mathbf {x}}(f,g) \mathop {}\!\mathrm {d}{x}}{\int _{JS} 1 \mathop {}\!\mathrm {d}{x}} = \frac{\sum _{k} \int _{l_k} \kappa _{\mathbf {x}}(f,g) \mathop {}\!\mathrm {d}{x}}{\sum _{k} \int _{l_k} 1 \mathop {}\!\mathrm {d}{x}} \\&\approx \frac{\sum _{k} \frac{1}{2} \left( \vert \kappa _{\mathbf {p}_{k_i}}(f,g)\vert + \vert \kappa _{\mathbf {p}_{k_j}}(f,g)\vert \right) \Vert \mathbf {p}_{k_j}-\mathbf {p}_{k_i}\Vert _2}{\sum _k \Vert \mathbf {p}_{k_j}-\mathbf {p}_{k_i}\Vert _2}. \end{aligned}$$

In short, the measure computes the deviation of the Jacobi set with regard to the globally computed gradient alignment field \(\kappa _{\mathbf {x}}(f,g)\). The background of this measure is that the gradient alignment value is zero for \({\mathbf {x}}\in {{\mathbb J}}(f,g)\).

5.1 Analytic dataset

The first dataset consists of two artificially generated scalar fields. Both are constructed by the sum of three bivariate normal distributions on the unit square. To get an impression of the two functions, a visualization of the contour lines is presented in Fig. 7. The figure also shows the Jacobi set of these two functions (black line) given by an analytical formula. Therefore, we can compare the Jacobi set extracted by our local bilinear approach (or by the piecewise linear approach) with the true Jacobi set.

In Fig. 1, the Jacobi sets are computed by the piecewise linear approach (top row) and our local bilinear method (bottom row) for a fixed resolution and different zoom levels on a (triangulated) rectangular grid. First of all, both methods identify the fundamental topological structure correctly. For each zoom level, the piecewise linear approach produces a solution that highly suffers from the edge-based geometric representation of the Jacobi set (which stems from the underlying triangulation), leading to zig-zag patterns. Furthermore, the zoomed-in image (top right) reveals that the Jacobi set representation consists of several (“glued”) triangles of the underlying triangulation, resulting in misleading topological patterns. While our local bilinear method obtains the same topology, these triangles are merged geometrically, leading to a clearer geometric representation. In sum, our local bilinear method results in a smoother and more precise Jacobi set representation (e.g., see third column).

Fig. 8
figure 8

Comparison of 0, 1, 2, and 4 subdivision steps with adjusted zoom levels (left to right) for the piecewise linear (top) and local bilinear (bottom) method using the analytic dataset on a triangulated mesh with \(80 \times 80\) data points. The globally computed gradient alignment values are not interpolated to emphasize the subdivision process

Full size image

In the following, we also evaluate the proposed local subdivision method. It can be applied to both our local bilinear method and the piecewise linear method. The qualitative results are presented in Fig. 8, and the corresponding gradient alignment measure is depicted in Fig. 9.

In general, both Jacobi set representations produce incorrectly detected regions and artifacts for the initial configuration, especially at the bottom right. This is due to the coarse irregular mesh and resulting degenerate areas. With the application of subdivision, both methods produce better results; however, our local bilinear method results in much smoother representations. This observation can also be noticed in the error plot in Fig. 9. The gradient alignment measure shows that our approach results in less error and has a faster convergence than the piecewise linear method.

5.2 Von Kármán vortex street dataset

While the analytic dataset provides first insights into our approach, we now apply our method to a simulated von Kármán vortex street [15]. The dataset consists of 1501 time steps describing the velocity and has a resolution of \(640 \times 80\). We use the magnitudes of the flow velocity for two consecutive time steps as the two scalar fields for the Jacobi set computation. For our examples, we start at time step 1500, where the vortex street is fully emerged.

Fig. 9
figure 9

The gradient alignment measure for different subdivision steps (analogously to Fig. 8) for the piecewise linear (red) and our local bilinear (blue) method. The vertical dashed lines correspond to the snapshots in Fig. 8

Full size image

A visualization of the von Kármán vortex street for this time step is depicted in Fig. 10 top. The figure also shows the Jacobi set computed by the piecewise linear approach (middle) and our approach (bottom). In general, we observe that the Jacobi set captures the topological structure of each Kármán vortex. However, similar to previous observations, the zig-zag patterns of the piecewise linear approach make it hard to distinguish between different topological structures.

For a zoomed-in view, the top rows of Fig. 11 show the framed area in Fig 10 in more detail. We observe that both methods fail to produce the correct topological structure at the top left (compare the gradient alignment field in the background). However, due to our connection method, our Jacobi set representation suggests that this region is problematic and may contain wrongly detected areas. In the piecewise linear case, the regular identification of Jacobi set patterns via the underlying triangulation makes it hard to distinguish between correctly and incorrectly detected areas. Besides of that, at the middle and top right areas, our local bilinear method captures the geometry better due to the smooth Jacobi set representation.

Fig. 10
figure 10

LIC visualization of the fully emerged von Kármán vortex street (top) as well as a comparison of the Jacobi set computed with the piecewise linear method (middle) and our method (bottom). The two scalar fields represent the flow velocity magnitude for two consecutive time steps. The boxed-in areas will be discussed in more detail in Fig. 11

Full size image
Fig. 11
figure 11

For the piecewise linear (left) and local bilinear (right) computation of the Jacobi set, the top rows show the zoomed-in view of Fig. 10 (see the white box). As scalar functions, flow magnitudes of two consecutive time steps are used. Furthermore, the subdivision method is applied in the zoomed-in areas for both methods

Full size image

Another comparison of these two methods is done by using the local subdivision method (rows 2–4 in Fig. 11). We observe for both methods that the incorrect topological structures in the top left disappear after one subdivision step. Another important aspect is shown in the third row (with two subdivision steps). Topologically identified patterns, such as the isolated triangle at the bottom left, can disappear visually for our bilinear method due to geometrical contraction. This can never happen for the piecewise linear approach. Applying subdivision four times, we observe that the representation of topological structures is significantly improved. While the piecewise linear approach identifies the circular shape rather poorly (due to the underlying grid), the geometry of our method captures the circularity more clearly (in the limit, the shape is nearly an ellipse).

Fig. 12
figure 12

Comparison of the piecewise linear (a) and local bilinear (b) computation of Jacobi sets for the Hurricane Isabel dataset. For the Jacobi set, a pressure and temperature scalar field is used. Furthermore, our local bilinear method with two subdivision steps is illustrated (c)

Full size image

5.3 Hurricane Isabel dataset

Jacobi sets are motivated as a topological descriptor of multiple scalar fields with different quantities. Here, we perform the Jacobi set extraction on the multi-field real-world dataset Hurricane IsabelFootnote 1. The dataset consists of multiple 3D scalar fields and a 3D velocity vector field that have a resolution of \(500\times 500\times 100\) and 48 time steps.

We use the pressure and temperature scalar field at time step 30 and height 50 to compare the Jacobi set computation methods in Fig. 12. At this height, the hurricane has a large spatial expansion and reveals many characteristic structures.

Comparing the piecewise linear method (Fig. 12a) with our method (Fig.12b), we observe that many areas are marked in the top left region. Whereas in the piecewise linear case it is nearly impossible to track topological structures, our method (without subdivision) already has a clearer representation due to geometrical enhancements. However, it can be observed that the preservation of topology leads to a folding of line segments, which can clutter areas in the representation (see exemplary Fig. 5). Our subdivision method (Fig 12c) solves this issue by thinning out those areas. This leads to a much clearer representation.

To further demonstrate that our proposed local subdivision method improves the results, the other zoomed-in area at the center shows that the identified topological structures match more clearly the zero-level set (white areas) of the gradient alignment field in the background. In fact, several connected topological patterns are separated correctly.

6 Conclusion

In this paper, we recapped the piecewise linear computation of Jacobi sets and embedded its theory into our new formulation. This view enables a new formulation that extends the piecewise linear computation to be based on a bilinear interpolation scheme. While preserving the topological structures, our bilinear interpolation results in a smoother and geometrically more accurate Jacobi set representation. In addition, our efficient local subdivision method tailored to our approach further improves the Jacobi set representation.

In the future, we could extend our local bilinear method to higher dimensions as well as more than two scalar functions. Additionally, other interpolation methods could be used that are based on finite elements or higher interpolation schemes such as biquadratic or bicubic interpolation.

Another idea is to evaluate our local bilinear method in terms of detecting new features. This not only includes the raw results but also the representation via connected line segments. In this regard, the appearance and the spatial spread of the connected line segments (representing a band-like structure) could contain more information about the underlying data, e.g., uncertainty or other features. In addition, since our method significantly facilitates the investigation of Jacobi sets, another research direction is to find new interpretations and applications of Jacobi sets across diverse research areas, such as image processing or computer vision.