Skip to main content
SpringerLink
Log in

Corner error reduction by Chebyshev transformed orthogonal grid

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

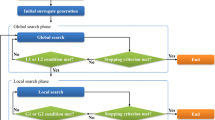
In the context of surrogate-based optimization, the efficient global exploration of the design space strongly relies on the overall accuracy of the surrogate model. For most modeling approaches, significant inaccuracies are often observed at the outlier region of the design space, where very few samples are spotted, known as the “corner error”. Inspired by the Runge effect originating from equidistant samples, a Chebyshev-transformed Orthogonal Latin Hypercube sampling approach is proposed to alleviate corner errors. An initial OLH sample was generated on a unit hyper-sphere, and its radial projection was used as the start of a sequential sampling process. The acquisition function uses the confidence interval of the Kriging predictor, combined with the min–max-distance criterion. To testify the proposed approach, models built with ordinary OLH grids are compared to the models built with Chebyshev-transformed OLH grids. Benchmark tests were performed on a series of multimodal functions, four 2-dimensional functions, and three 6-dimensional functions, both the root mean-squared error and the maximum error were reduced compared with the OLH design for most of the tests. This approach was applied to increase the pressure rise of the engine cooling fan without reducing the efficiency, for which 2.5% higher pressure rise was gained compared to the reference design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Algorithm 1
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Data Availability

No datasets were generated or analysed during the current study.

References

  1. Jiang C, Zheng J, Han X (2018) Probability-interval hybrid uncertainty analysis for structures with both aleatory and epistemic uncertainties: A review. Struct Multidisc Optim 57:2485–2502

    Article  Google Scholar 

  2. Zhang X, Wu Z, Ma H (2021) An effective Kriging-based approximation for structural reliability analysis with random and interval variables. Struct Multidisc Optim 63:2473–2491

    Article  MathSciNet  Google Scholar 

  3. Ye P, Pan G (2023) Multi-surrogates and multi-points infill strategy-based global optimization method. Eng Comput 39(2):1617–1636

    Article  Google Scholar 

  4. Qian HY (2022) Numerical simulation of stress-based topological optimization of continuum structures under casting constraints. Eng Comput 6:4919–4945

    Google Scholar 

  5. Tang Z, Hu X, Périaux J (2020) Multi-level hybridized optimization methods coupling local search deterministic and global search evolutionary algorithms. Arch Comput Methods Eng 3:939–975

    Article  MathSciNet  Google Scholar 

  6. Jones DR, Martins JRRA (2021) The direct algorithm: 25 years later. J Global Optim 3:521–566

    Article  MathSciNet  Google Scholar 

  7. Pang Y, Lai X, Zhang S, Wang Y, Yang L, Song X (2023) A Kriging-assisted global reliability-based design optimization algorithm with a reliability-constrained expected improvement. Appl Math Model 2:611–630

    Article  MathSciNet  Google Scholar 

  8. Dong GY, Lemieux C (2022) Dependence properties of scrambled Halton sequences. Math Comput Simul 200:240–262

    Article  MathSciNet  Google Scholar 

  9. Zhang T, Yang C, Chen H, Sun L, Deng K (2020) Multi-objective optimization operation of the green energy island based on Hammersley sequence sampling. Energy Convers Manag 204:112316

    Article  Google Scholar 

  10. Belov AA, Tintul MA (2022) Calculating multidimensional cubatures on Sobol sequences. Bull Russ Acad Sci Phys 7:856–860

    Article  Google Scholar 

  11. Cioppa T, Lucas TW (2007) Efficient nearly orthogonal and space-filling latin hypercubes. Technometrics 49:45–55

    Article  MathSciNet  Google Scholar 

  12. Zhang ZB, Demory B, et al (2014) Space infill study of Kriging meta-model for multi-objective optimization of an engine cooling fan. In: ASME Turbo Expo 2014: Turbine Technical Conference and Exposition

  13. Zhang Z, Han Z, Ferrand P (2019) High anisotropy space exploration with co-Kriging method. AIP Conf Proc 1:020029–14

    Google Scholar 

  14. Zhai Z, Li H, Wang X (2022) An adaptive sampling method for Kriging surrogate model with multiple outputs. Eng Comput 5:277–295

    Article  Google Scholar 

  15. Sanchez SM, Hong W (2011) Better than a petaflop: The power of efficient experimental design. In: Proceedings of the 2011 Winter Simulation Conference (WSC)

  16. Fang K (1994) Uniform design and uniform design table. Science Press, Beijing

    Google Scholar 

  17. Fang K, Ma C, Winker P (2002) Centered l\(_2\)-discrepancy of random sampling and latin hypercube design, and construction of uniform designs. Math Comput 237:275–296

    Google Scholar 

  18. Ye KQ (1998) Orthogonal column latin hypercubes and their application in computer experiments. J Am Stat Assoc 444:1430–1439

    Article  MathSciNet  Google Scholar 

  19. Wu X, Zhang W, Song S (2018) Robust aerodynamic shape design based on an adaptive stochastic optimization framework. Struct Multidiscip Optim 2:639–651

    Article  MathSciNet  Google Scholar 

  20. Lämmle S, Bogoclu C, Cremanns K, Roos D (2023) Gradient and uncertainty enhanced sequential sampling for global fit. Comput Methods Appl Mech Eng 11:6226

    MathSciNet  Google Scholar 

  21. Fang H, Gong C, Li C, Zhang Y, Ronch AD (2021) A sequential optimization framework for simultaneous design variables optimization and probability uncertainty allocation. Struct Multidiscip Optim 3:1307–1325

    Article  MathSciNet  Google Scholar 

  22. Li YH, Wu YZ, Huang ZD (2014) An incremental Kriging method for sequential optimal experimental design. CMES-Comput Model Eng Sci 4:323–357

    Google Scholar 

  23. Qian J, Yi J, Cheng Y, Liu J, Zhou Q (2020) A sequential constraints updating approach for Kriging surrogate model-assisted engineering optimization design problem. Eng Comput 3:993–1009

    Article  Google Scholar 

  24. Li K, Huang H, Fu S, Ma C, Fan Q, Zhu Y (2023) A multi-strategy enhanced northern goshawk optimization algorithm for global optimization and engineering design problems. Comput Methods Appl Mech Eng 11:6199

    MathSciNet  Google Scholar 

  25. Ullrich T (2008) Smolyak’s algorithm, sampling on sparse grids and sobolev spaces of dominating mixed smoothness. East J Approx 1:1–38

    MathSciNet  Google Scholar 

  26. Plaskota L, Wasilkowski GW (2004) Smolyak’s algorithm for integration and l\(_1\) -approximation of multivariate functions with bounded mixed derivatives of second order. Numer Algor 3:229–246

    Article  Google Scholar 

  27. Kieslich CA, Boukouvala F, Floudas CA (2018) Optimization of black-box problems using smolyak grids and polynomial approximations. J Global Optim 4:845–869

    Article  MathSciNet  Google Scholar 

  28. Beyer HG, Sendhoff B (2007) Robust optimization—a comprehensive survey. Comput Methods Appl Mech Eng 33–34:3190–3218

    Article  MathSciNet  Google Scholar 

  29. Johnson ME, Moore LM, Ylvisaker D (1990) Minimax and maximin distance designs. J Stat Plan Infer 2:131–148

    Article  MathSciNet  Google Scholar 

  30. Kleijnen JPC, Sanchez SM, Lucas TW (2005) State-of-the-art review: A user’s guide to the brave new world of designing simulation experiments. INFORMS J Comput 3:263–289

    Article  Google Scholar 

  31. Smolyak SA (1963) Quadrature and interpolation formulas for tensor products of certain classes of functions. Dokl Akad Nauk SSSR 5:1042–1045

    Google Scholar 

  32. Trefethen LN (2013) Approximation theory and approximation practice. Society for Industrial and Applied Mathematics (SIAM), Philadelphia

    Google Scholar 

  33. Wu J, Luo Z, Zhang N, Zhang Y (2015) A new interval uncertain optimization method for structures using Chebyshev surrogate models. Comput Struct (C) 2:185–196

    Article  Google Scholar 

  34. Fu C, Zhu W, Yang Y, Zhao S, Lu K (2022) Surrogate modeling for dynamic analysis of an uncertain notched rotor system and roles of Chebyshev parameters. J Sound Vib 11:6755

    Google Scholar 

  35. Fu C, Wang P, Zhao L, Wang X (2020) A distance correlation-based Kriging modeling method for high-dimensional problems. Knowl-Based Syst 206:106356

    Article  Google Scholar 

  36. Laurenceau J, Sagaut P (2008) Building efficient response surfaces of aerodynamic functions with Kriging and Cokriging. Am Inst Aeronaut Astronaut 46:2

    Article  Google Scholar 

  37. Zebin Z, Pengfei Z, Hong G, Yong L (2019) Implementation of Kriging model based sequential design on the optimization of sliding bearing. J Harbin Inst Technol 51:7

    Google Scholar 

  38. Yao X (1999) Evolutionary programming made faster. IEEE Trans Evol Comput 2:82–102

    Google Scholar 

  39. Adorio EP, Diliman UP (2005) MVF-multivariate test functions library in C for unconstrained global optimization

  40. Branin FH (1972) Widely convergent method for finding multiple solutions of simultaneous nonlinear equations. IBM J Res Dev 5:504–522

    Article  MathSciNet  Google Scholar 

  41. Picheny V, Wagner T, Ginsbourger D (2013) A benchmark of Kriging-based infill criteria for noisy optimization. Struct Multidiscip Optim 3:607–626

    Article  Google Scholar 

  42. Gaviano M, Kvasov DE, Lera D, Sergeyev YD (2003) Algorithm 829: Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans Math Softw 4:469–480

    Article  MathSciNet  Google Scholar 

  43. Zhang Z, Li Y (2022) Exploration of anisotropic design space by using unified taylor-cokriging method. Appl Math Model 2:45–60

    Article  MathSciNet  Google Scholar 

  44. Rosenbrock HH (1960) A automatic method for finding the greatest or least value of a function. Comput J 3:174–184

    Article  MathSciNet  Google Scholar 

  45. Hartman JK (1973) Some experiments in global optimization. Naval Res Logist Quart 3:569–576

    Article  Google Scholar 

  46. Kohonen T (1990) The self-organizing map. Proc IEEE 9:1464–1480

    Article  Google Scholar 

  47. Zhang ZB, Zhang PF, Li RZ (2020) Som-based high-dimensional design spaces mapping for multi-objective optimization. J Northwestern Polytech Univ 38(3):677–684

    Article  Google Scholar 

  48. Soulat L, Ferrand P, Moreau S, Aubert S, Buisson M (2013) Efficient optimisation procedure for design problems in fluid mechanics. Comput Fluids 2:73–86

    Article  MathSciNet  Google Scholar 

  49. Martins JRRA, Kennedy GJ (2021) Enabling large-scale multidisciplinary design optimization through adjoint sensitivity analysis. Struct Multidiscip Optim 5:2959–2974

    Article  Google Scholar 

  50. Ohashi M, Tokugawa N (2021) Adjoint-based sensitivity analysis for airfoil flow control aiming at lift-to-drag ratio improvement. Am Inst Aeronaut Astronaut 11:4437–4448

    Article  Google Scholar 

  51. Zhang Z, Buisson M, Ferrand P, Henner M, Gillot F (2015) Meta-model based optimization of a large diameter semi-radial conical hub engine cooling fan. Mech Ind 2:2

    Google Scholar 

  52. Ribaud M, Blanchet-Scalliet C, Helbert C, Gillot F (2020) Robust optimization: a Kriging-based multi-objective optimization approach. Reliab Eng Syst Saf 3:106913

    Article  Google Scholar 

  53. Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning, 1st edn. Longman Publishing Co., Inc, Boston

    Google Scholar 

Download references

Acknowledgements

The author would like to thank the anonymous reviewers and the editors for carefully reading the paper and for making useful comments and suggestions that improved the appearance of the paper. This work was supported by the National Supercomputing Center in Zhengzhou. The authors acknowledge  HEXAGON MSC CRADLE  for the CFD solver licenses provided. The authors also want to acknowledge Mr.Bruno Demory and Dr.Manuel Henner of Valeo Thermal Systems for the inspiring talks during coffee breaks.

Funding

This work was financed by the National Natural Science Foundation of China [Grant number 12272354 and 52375270], and the Natural Science Foundation of Henan (Grant number 222300420547).

Author information

Authors and Affiliations

  1. School of Mechanical and Power Engineering, Zhengzhou University, Kexue Avenue, Zhengzhou, 450001, Henan, China

    Zebin Zhang, Shizhao Jing & Xianzong Meng

  2. School of Mechanical and Electrical Engineering, Xuchang University, Bayi Road, Xuchang, 461000, Henan, China

    Yaohui Li

Authors
  1. Zebin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shizhao Jing
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yaohui Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xianzong Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Conceptualization and resources were provided by Z.Z.. Methodology was proposed by Z.Z. and S.J.. Funding acquisition was provided by Z.Z. and Y.L.. Data collection, analysis and validation were performed by S.J.. The first draft of the manuscript was written by Z.Z. and S.J. and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Zebin Zhang.

Ethics declarations

Conflict of interest

The authors declare that there is no Conflict of interest regarding the publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Z., Jing, S., Li, Y. et al. Corner error reduction by Chebyshev transformed orthogonal grid. Engineering with Computers (2024). https://doi.org/10.1007/s00366-024-01991-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00366-024-01991-3

Keywords

Search

Navigation