Skip to main content
SpringerLink
Log in

A novel deep unsupervised learning-based framework for optimization of truss structures

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

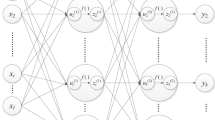
In this paper, an efficient deep unsupervised learning (DUL)-based framework is proposed to directly perform the design optimization of truss structures under multiple constraints for the first time. Herein, the members’ cross-sectional areas are parameterized using a deep neural network (DNN) with the middle spatial coordinates of truss elements as input data. The parameters of the network, including weights and biases, are regarded as decision variables of the structural optimization problem, instead of the member’s cross-sectional areas as those of traditional optimization algorithms. A new loss function of the network model is constructed with the aim of minimizing the total structure weight so that all constraints of the optimization problem via unsupervised learning are satisfied. To achieve the optimal parameters, the proposed model is trained to minimize the loss function by a combination of the standard gradient optimizer and backpropagation algorithm. As soon as the learning process ends, the optimum weight of truss structures is indicated without utilizing any other time-consuming metaheuristic algorithms. Several illustrative examples are investigated to demonstrate the efficiency of the proposed framework in requiring much lower computational cost against other conventional methods, yet still providing high-quality optimal solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Kaveh A, Mahjoubi S (2019) Hypotrochoid spiral optimization approach for sizing and layout optimization of truss structures with multiple frequency constraints. Eng Comput 35:1443–1462

    Google Scholar 

  2. Ho-Huu V, Vo-Duy T, Luu-Van T, Le-Anh L, Nguyen-Thoi T (2016) Optimal design of truss structures with frequency constraints using improved differential evolution algorithm based on an adaptive mutation scheme. Autom Constr 68:81–94

    Google Scholar 

  3. Kaveh A, Talatahari S (2009) Size optimization of space trusses using big bang-big crunch algorithm. Comput Struct 87:1129–1140

    Google Scholar 

  4. Khot N (1983) Nonlinear analysis of optimized structure with constraints on systemstability. AIAA J 21:1181–1186

    MATH  Google Scholar 

  5. Khot N, Kamat M (1985) Minimum weight design of truss structures with geometric nonlinear behavior. AIAA J 23:139–144

    MATH  Google Scholar 

  6. El-Sayed ME, Ridgely BJ, Sandgren E (1989) Nonlinear structural optimization using goal programming. Comput Struct 32:69–73

    MATH  Google Scholar 

  7. Saka M, Ulker M (1992) Optimum design of geometrically nonlinear space trusses. Comput Struct 42:289–299

    Google Scholar 

  8. Shin M-K, Park K-J, Park G-J (2007) Optimization of structures with nonlinear behavior using equivalent loads. Comput Methods Appl Mech Eng 196:1154–1167

    MATH  Google Scholar 

  9. Miguel LFF, Miguel LFF (2012) Shape and size optimization of truss structures considering dynamic constraints through modern metaheuristic algorithms. Expert Syst Appl 39:9458–9467

    Google Scholar 

  10. Lieu QX, Do DT, Lee J (2018) An adaptive hybrid evolutionary firefly algorithm for shape and size optimization of truss structures with frequency constraints. Comput Struct 195:99–112

    Google Scholar 

  11. Gomes HM (2011) Truss optimization with dynamic constraints using a particle swarm algorithm. Expert Syst Appl 38:957–968

    Google Scholar 

  12. Kaveh A, Zolghadr A (2014) Democratic pso for truss layout and size optimization with frequency constraints. Comput Struct 130:10–21

    Google Scholar 

  13. Toğan V, Daloğlu AT (2006) Optimization of 3d trusses with adaptive approach in genetic algorithms. Eng Struct 28:1019–1027

    Google Scholar 

  14. Zuo W, Bai J, Li B (2014) A hybrid oc-ga approach for fast and global truss optimization with frequency constraints. Appl Soft Comput 14:528–535

    Google Scholar 

  15. Pierezan J, dos Santos Coelho L, Mariani VC, de Vasconcelos Segundo EH, Prayogo D (2021) Chaotic coyote algorithm applied to truss optimization problems. Comput Struct 242:106353

    Google Scholar 

  16. Lee KS, Geem ZW (2004) A new structural optimization method based on the harmony search algorithm. Comput Struct 82:781–798

    Google Scholar 

  17. Buntara G, Takahiro H, Aylie H, Alisjahbana S, As’ad S (2017) Evolutionary aco algorithms f or truss optimization problems. Proc Eng 171:1100–1107

  18. Kaveh A, Zakian P (2018) Improved gwo algorithm for optimal design of truss structures. Eng Comput 34:685–707

    Google Scholar 

  19. Degertekin S (2012) Improved harmony search algorithms for sizing optimization of truss structures. Comput Struct 92:229–241

    Google Scholar 

  20. Le-Duc T, Nguyen Q-H, Nguyen-Xuan H (2020) Balancing composite motion optimization. Inf Sci 520:250–270

    MathSciNet  Google Scholar 

  21. Fan H-Y, Lampinen J (2003) A trigonometric mutation operation to differential evolution. J Glob Optim 27:105–129

    MathSciNet  MATH  Google Scholar 

  22. Koo B, Jung R, Yu Y (2021) Automatic classification of wall and door bim element subtypes using 3d geometric deep neural networks. Adv Eng Inform 47:101200

    Google Scholar 

  23. Thorat Z, Mahadik S, Mane S, Mohite S, Udugade A (2019) Self driving car using raspberry-pi and machine learning. IRJET 06:969–972

  24. De Bruijne M (2016) Machine learning approaches in medical image analysis: from detection to diagnosis. Med Image Anal 33:94–97

  25. Na H, Kim S (2021) Predicting stock prices based on informed traders’ activities using deep neural networks. Econ Lett 204:109917

    MATH  Google Scholar 

  26. Jokar M, Semperlotti F (2021) Finite element network analysis: a machine learning based computational framework for the simulation of physical systems. Comput Struct 247:106484

    Google Scholar 

  27. Lee S, Kim H, Lieu QX, Lee J (2020) Cnn-based image recognition for topology optimization. Knowl Based Syst 198:105887

    Google Scholar 

  28. Papadopoulos V, Soimiris G, Giovanis D, Papadrakakis M (2018) A neural network-based surrogate model for carbon nanotubes with geometric nonlinearities. Comput Methods Appl Mech Eng 328:411–430

    MathSciNet  MATH  Google Scholar 

  29. Zhuang X, Guo H, Alajlan N, Zhu H, Rabczuk T (2021) Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur J Mech A Solids 87:104225

    MathSciNet  MATH  Google Scholar 

  30. Truong TT, Dinh-Cong D, Lee J, Nguyen-Thoi T (2020) An effective deep feedforward neural networks (dfnn) method for damage identification of truss structures using noisy incomplete modal data. J Build Eng 30:101244

    Google Scholar 

  31. Zhao J, Nguyen H, Nguyen-Thoi T, Asteris PG, Zhou J (2021) Improved Levenberg–Marquardt backpropagation neural network by particle swarm and whale optimization algorithms to predict the deflection of rc beams. Eng Comput 1–23. https://doi.org/10.1007/s00366-020-01267-6

  32. Truong TT, Lee J, Nguyen-Thoi T (2021) Joint damage detection of structures with noisy data by an effective deep learning framework using autoencoder-convolutional gated recurrent unit. Ocean Eng 243:110142

  33. Le HQ, Truong TT, Dinh-Cong D, Nguyen-Thoi T (2021) A deep feed-forward neural network for damage detection in functionally graded carbon nanotube-reinforced composite plates using modal kinetic energy. Front Struct Civ Eng 15:1453–1479

  34. Truong TT, Lee S, Lee J (2020) An artificial neural network-differential evolution approach for optimization of bidirectional functionally graded beams. Compos Struct 233:111517

    Google Scholar 

  35. Shariati M, Mafipour MS, Mehrabi P, Shariati A, Toghroli A, Trung NT, Salih MN (2021) A novel approach to predict shear strength of tilted angle connectors using artificial intelligence techniques. Eng Comput 37:2089–2109

    Google Scholar 

  36. Lee S, Vo TP, Thai H-T, Lee J, Patel V (2021) Strength prediction of concrete-filled steel tubular columns using categorical gradient boosting algorithm. Eng Struct 238:112109

    Google Scholar 

  37. Hajela P, Berke L (1991) Neurobiological computational models in structural analysis and design. Comput Struct 41:657–667

    MATH  Google Scholar 

  38. Hajela P, Berke L (1991) Neural network based decomposition in optimal structural synthesis. Comput Syst Eng 2:473–481

    MATH  Google Scholar 

  39. Adeli H, Park HS (1995) Optimization of space structures by neural dynamics. Neural Netw 8:769–781

    Google Scholar 

  40. Kang H-T, Yoon CJ (1994) Neural network approaches to aid simple truss design problems. Comput Aid Civ Infrastruct Eng 9:211–218

    Google Scholar 

  41. Ramasamy J, Rajasekaran S (1996) Artificial neural network and genetic algorithm for the design optimization of industrial roofs-a comparison. Comput Struct 58:747–755

    MATH  Google Scholar 

  42. Iranmanesh A, Kaveh A (1999) Structural optimization by gradient-based neural networks. Int J Numer Methods Eng 46:297–311

    MATH  Google Scholar 

  43. Mai HT, Kang J, Lee J (2021) A machine learning-based surrogate model for optimization of truss structures with geometrically nonlinear behavior. Finite Elem Anal Des 196:106461

    MathSciNet  Google Scholar 

  44. Nguyen LC, Nguyen-Xuan H (2020) Deep learning for computational structural optimization. ISA Trans 103:177–191

    Google Scholar 

  45. Ly DK, Truong TT, Nguyen-Thoi T (2021) Multi-objective optimization of laminated functionally graded carbon nanotube reinforced composite plates using deep feedforward neural networks-nsgaii algorithm. Int J Comput Methods. https://doi.org/10.1142/S0219876221500651

  46. Truong TT, Lee J, Nguyen-Thoi T (2021) Multi-objective optimization of multi-directional functionally graded beams using an effective deep feedforward neural network-smpso algorithm. Struct Multidiscip Optim 63:2889–2918

    MathSciNet  Google Scholar 

  47. Li B, Huang C, Li X, Zheng S, Hong J (2019) Non-iterative structural topology optimization using deep learning. Comput Aided Des 115:172–180

    Google Scholar 

  48. White DA, Arrighi WJ, Kudo J, Watts SE (2019) Multiscale topology optimization using neural network surrogate models. Comput Methods Appl Mech Eng 346:1118–1135

    MathSciNet  MATH  Google Scholar 

  49. Deng H, To AC (2021) A parametric level set method for topology optimization based on deep neural network. J Mech Des 143:091702

    Google Scholar 

  50. Abueidda DW, Koric S, Sobh NA (2020) Topology optimization of 2d structures with nonlinearities using deep learning. Comput Struct 237:106283

    Google Scholar 

  51. Nguyen-Thanh VM, Zhuang X, Rabczuk T (2020) A deep energy method for finite deformation hyperelasticity. Eur J Mech A/Solids 80:103874

    MathSciNet  MATH  Google Scholar 

  52. Li W, Bazant MZ, Zhu J (2021) A physics-guided neural network framework for elastic plates: comparison of governing equations-based and energy-based approaches. Comput Methods Appl Mech Eng 383:113933

    MathSciNet  MATH  Google Scholar 

  53. Guo H, Zhuang X, Rabczuk T (2021) A deep collocation method for the bending analysis of kirchhoff plate. arXiv:2102.02617

  54. Panghal S, Kumar M (2020) Optimization free neural network approach for solving ordinary and partial differential equations. Eng Comput 37:2989–3002

  55. Wang S, Wang H, Perdikaris P (2021) On the eigenvector bias of fourier feature networks: from regression to solving multi-scale pdes with physics-informed neural networks. Comput Methods Appl Mech Eng 384:113938

    MathSciNet  MATH  Google Scholar 

  56. Jin X, Cai S, Li H, Karniadakis GE (2021) Nsfnets (navier-stokes flow nets): physics-informed neural networks for the incompressible navier-stokes equations. J Comput Phys 426:109951

    MathSciNet  MATH  Google Scholar 

  57. Zhu Q, Liu Z, Yan J (2021) Machine learning for metal additive manufacturing: predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput Mech 67:619–635

    MathSciNet  MATH  Google Scholar 

  58. Chandrasekhar A, Suresh K (2021) Tounn: topology optimization using neural networks. Struct Multidiscip Optim 63:1135–1149

    MathSciNet  Google Scholar 

  59. Bradbury J, Frostig R, Hawkins P, Johnson MJ, Leary C, Maclaurin D, Wanderman-Milne S (2020) Jax: composable transformations of python+ numpy programs. 4:16. http://github.com/google/jax

  60. Kaveh A, Ghazaan MI (2015) Hybridized optimization algorithms for design of trusses with multiple natural frequency constraints. Adv Eng Softw 79:137–147

    Google Scholar 

  61. Kaveh A, Zolghadr A (2012) Truss optimization with natural frequency constraints using a hybridized css-bbbc algorithm with trap recognition capability. Comput Struct 102:14–27

    Google Scholar 

  62. Kaveh A, Azar BF, Talatahari S (2008) Ant colony optimization for design of space trusses. Int J Space Struct 23:167–181

    Google Scholar 

  63. Sonmez M (2011) Artificial bee colony algorithm for optimization of truss structures. Appl Soft Comput 11:2406–2418

    Google Scholar 

  64. Hasançebi O (2008) Adaptive evolution strategies in structural optimization: enhancing their computational performance with applications to large-scale structures. Comput Struct 86:119–132

    Google Scholar 

  65. Cao X, Sugiyama Y, Mitsui Y (1998) Application of artificial neural networks to load identification. Comput Struct 69:63–78

    MATH  Google Scholar 

  66. Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv:1412.6980

  67. Camarda CJ, Adelman HM (1984) Static and dynamic structural-sensitivity derivative calculations in the finite-element-based engineering analysis language (eal) system. No. NASA-TM-85743

  68. Chandrasekhar A, Sridhara S, Suresh K (2021) Auto: a framework for automatic differentiation in topology optimization. arXiv:2104.01965

  69. Lee S, Ha J, Zokhirova M, Moon H, Lee J (2018) Background information of deep learning for structural engineering. Arch Comput Methods Eng 25:121–129

    MathSciNet  MATH  Google Scholar 

  70. Paul M (2018) Applied machine learning. https://cmci.colorado.edu/classes/INFO-4604/resources.html. Accessed 19 Apr 2021

  71. Khatibinia M, Naseralavi SS (2014) Truss optimization on shape and sizing with frequency constraints based on orthogonal multi-gravitational search algorithm. J Sound Vib 333:6349–6369

    Google Scholar 

  72. Degertekin S, Bayar GY, Lamberti L (2021) Parameter free jaya algorithm for truss sizing-layout optimization under natural frequency constraints. Comput Struct 245:106461

    Google Scholar 

  73. Camp CV (2007) Design of space trusses using big bang-big crunch optimization. J Struct Eng 133:999–1008

    Google Scholar 

  74. Li L, Huang Z, Liu F, Wu Q (2007) A heuristic particle swarm optimizer for optimization of pin connected structures. Comput Struct 85:340–349

    Google Scholar 

  75. Degertekin S, Hayalioglu M (2013) Sizing truss structures using teaching-learning-based optimization. Comput Struct 119:177–188

    Google Scholar 

  76. Lamberti L (2008) An efficient simulated annealing algorithm for design optimization of truss structures. Comput Struct 86:1936–1953

    Google Scholar 

  77. Mohamed AW, Sabry HZ (2012) Constrained optimization based on modified differential evolution algorithm. Inf Sci 194:171–208

    Google Scholar 

  78. Mallipeddi R, Suganthan PN, Pan Q-K, Tasgetiren MF (2011) Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl Soft Comput 11:1679–1696

    Google Scholar 

  79. Pan Q-K, Suganthan PN, Wang L, Gao L, Mallipeddi R (2011) A differential evolution algorithm with self-adapting strategy and control parameters. Comput Oper Res 38:394–408

    MathSciNet  MATH  Google Scholar 

  80. Rao RV, Kalyankar V, Waghmare G (2014) Parameters optimization of selected casting processes using teaching-learning-based optimization algorithm. Appl Math Model 38:5592–5608

    Google Scholar 

  81. Wang D, Tan D, Liu L (2018) Particle swarm optimization algorithm: an overview. Soft Comput 22:387–408

    Google Scholar 

  82. Ho-Huu V, Nguyen-Thoi T, Vo-Duy T, Nguyen-Trang T (2016) An adaptive elitist differential evolution for optimization of truss structures with discrete design variables. Comput Struct 165:59–75

    Google Scholar 

  83. Yam JY, Chow TW (2000) A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 30:219–232

    Google Scholar 

  84. Ng A (2019) Machine learning yearning: technical strategy for AI engineers in the era of deep learning [online]. https://www.deeplearning.ai/machine-learning-yearning/

Download references

Acknowledgements

This research was supported by a grant (NRF-2021R1A4A2002855) from NRF (National Research Foundation of Korea) funded by MEST (Ministry of Education and Science Technology) of Korean government.

Author information

Authors and Affiliations

  1. Deep Learning Architectural Research Center, Sejong University, 209 Neungdong-ro, Gwangjin-gu, Seoul, 05006, Republic of Korea

    Hau T. Mai & Jaehong Lee

  2. Faculty of Mechanical Engineering, Industrial University of Ho Chi Minh City, 12 Nguyen Van Bao Street, Ward 4, Go Vap District, Ho Chi Minh City, 70000, Vietnam

    Hau T. Mai

  3. Faculty of Civil Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, Ward 14, District 10, Ho Chi Minh City, Vietnam

    Qui X. Lieu

  4. Vietnam National University Ho Chi Minh City (VNU-HCM), Linh Trung Ward, Thu Duc District, Ho Chi Minh City, Vietnam

    Qui X. Lieu

  5. School of Architecture, Yeungnam University, 280, Daehak-Ro, Gyeongsan, Gyeongbuk, 38541, Republic of Korea

    Joowon Kang

Authors
  1. Hau T. Mai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qui X. Lieu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Joowon Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jaehong Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Hau T. Mai: conceptualization, methodology, software, formal analysis, investigation, writing - original draft, writing—review and editing, visualization. Qui X. Lieu: methodology, writing—original draft, writing—review and editing. Joowon Kang: data curation, validation, resources. Jaehong Lee: conceptualization, methodology, supervision, funding acquisition.

Corresponding author

Correspondence to Jaehong Lee.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mai, H.T., Lieu, Q.X., Kang, J. et al. A novel deep unsupervised learning-based framework for optimization of truss structures. Engineering with Computers 39, 2585–2608 (2023). https://doi.org/10.1007/s00366-022-01636-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-022-01636-3

Keywords

Search

Navigation