Skip to main content
SpringerLink
Log in

Magnetostriction-assisted active control of the multi-layered nanoplates: effect of the porous functionally graded facesheets on the system’s behavior

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

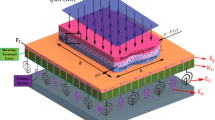
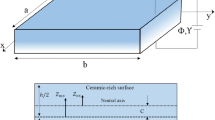
The current study aims to analyze the vibrational behavior of a three-layered composite sandwich of magnetostrictive nanoplate integrated with functionally graded material facesheets. The core layer is supposed to be consisted of Terfenol-D and the top and the bottom plies are supposed to be from functionally graded material. To consider the small-scale effect, the Eringen’s nonlocal theory is utilized. On the other hand, kinematic relations of the nanoplate, i.e. rested on a Winkler–Pasternak medium, are expressed based on the first-order shear deformation theory. The governing equations are derived by employing the Hamilton’s principle and solved analytically by applying the Navier’s method for the simply supported boundary condition. The effects of various parameters such as nonlocal parameter, Winkler and Pasternak foundation, gradient index, feedback gain, and aspect ratio on the dynamic behaviors of the system are monitored in detail. To exhibit the accuracy and validity of the present study, our results are compared to those available in the literature. The results indicate when the thickness of the magnetostrictive layer increase, natural frequencies also increase. The results of the present study can be utilized in designing mechanical nanosensors, actuators, vibration cancellation, and smart nanovalves in injectors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Abbreviations

FGM:

Functionally graded material

FSDT:

First-order shear deformation theory

References

  1. Arani AG, Arani HK, Maraghi ZK (2015) Vibration analysis of rectangular magnetostrictive plate considering thickness variation in two directions. Int J Appl Mech 07(04):1550059

    Google Scholar 

  2. Arani AG, Maraghi ZK, Arani HK (2016) Orthotropic patterns of Pasternak foundation in smart vibration analysis of magnetostrictive nanoplate. Proc Inst Mech Eng Part C 230(4):559–572

    Google Scholar 

  3. Ebrahimi F, Barati MR (2017) Electro-magnetic effects on nonlocal dynamic behavior of embedded piezoelectric nanoscale beams. J Intell Mater Syst Struct 28(15):2007–2022

    Google Scholar 

  4. Ebrahimi F, Dabbagh A (2018) Thermo-magnetic field effects on the wave propagation behavior of smart magnetostrictive sandwich nanoplates. Eur Phys J Plus 133(3):97

    Google Scholar 

  5. Ebrahimi F, Dabbagh A (2018) Wave propagation analysis of magnetostrictive sandwich composite nanoplates via nonlocal strain gradient theory. Proc Inst Mech Eng Part C 232(22):4180–4192

    Google Scholar 

  6. Ebrahimi F, Dabbagh A, Rabczuk T (2021) On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Eur J Mech A 85:104130

    MathSciNet  MATH  Google Scholar 

  7. Ebrahimi F, Dabbagh A, Tornabene F, Civalek O (2019) Hygro-thermal effects on wave dispersion responses of magnetostrictive sandwich nanoplates. Adv Nano Res 7(3):157–167

    Google Scholar 

  8. Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2021) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput 37(2):921–936

    Google Scholar 

  9. Eringen AC, Edelen DGB (1972) On nonlocal elasticity. Int J Eng Sci 10(3):233–248

    MathSciNet  MATH  Google Scholar 

  10. Fang J, Zheng S, Xiao J, Zhang X (2020) Vibration and thermal buckling analysis of rotating nonlocal functionally graded nanobeams in thermal environment. Aerosp Sci Technol 106:6146

    Google Scholar 

  11. Fenjan RM, Hamad LB, Faleh NM (2020) Mechanical-hygro-thermal vibrations of functionally graded porous plates with nonlocal and strain gradient effects. Adv Aircr Spacecr Sci 7(2):169–186

    Google Scholar 

  12. Ghobadi A, Golestanian H, Beni YT, Żur KK (2021) On the size-dependent nonlinear thermo-electro-mechanical free vibration analysis of functionally graded flexoelectric nano-plate. Commun Nonlinear Sci Numer Simul 95:105585

    MathSciNet  MATH  Google Scholar 

  13. Ghobadi A, Tadi Beni Y, Kamil Żur K (2021) Porosity distribution effect on stress, electric field and nonlinear vibration of functionally graded nanostructures with direct and inverse flexoelectric phenomenon. Compos Struct 259:113220

    Google Scholar 

  14. Gholipour A, Ghayesh MH (2020) A coupled nonlinear nonlocal strain gradient theory for functionally graded Timoshenko nanobeams. Microsyst Technol 26(6):2053–2066

    Google Scholar 

  15. Ghorbani K, Rajabpour A, Ghadiri M, Keshtkar Z (2020) Investigation of surface effects on the natural frequency of a functionally graded cylindrical nanoshell based on nonlocal strain gradient theory. Eur Phys J Plus 135(9):701

    Google Scholar 

  16. Ghorbanpour Arani A, Khani Arani H, Khoddami Maraghi Z (2019) Size-dependent in vibration analysis of magnetostrictive sandwich composite micro-plate in magnetic field using modified couple stress theory. J Sandwich Struct Mater 21(2):580–603

    MATH  Google Scholar 

  17. Ghorbanpour Arani A, Khoddami Maraghi Z (2016) A feedback control system for vibration of magnetostrictive plate subjected to follower force using sinusoidal shear deformation theory. Ain Shams Eng J 7(1):361–369

    Google Scholar 

  18. Ghorbanpour Arani A, Khoddami Maraghi Z, Khani Arani H (2016) Orthotropic patterns of Pasternak foundation in smart vibration analysis of magnetostrictive nanoplate. Proc Inst Mech Eng Part C 230(4):559–572

    MATH  Google Scholar 

  19. Hebali H, Tounsi A, Houari MSA, Bessaim A, Bedia EAA (2014) New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J Eng Mech 140(2):374–383

    Google Scholar 

  20. Heidari Y, Arefi M, Irani Rahaghi M (2020) Nonlocal vibration characteristics of a functionally graded porous cylindrical nanoshell integrated with arbitrary arrays of piezoelectric elements. Mech Based Des Struct Mach 1–28. https://doi.org/10.1080/15397734.2020.1830799

  21. Hieu D-V, Duong T-H, Bui G-P (2020) Nonlinear vibration of a functionally graded nanobeam based on the nonlocal strain gradient theory considering thickness effect. Adv Civil Eng 2020:9407673

    Google Scholar 

  22. Hoa LK, Vinh PV, Duc ND, Trung NT, Son LT, Thom DV (2020) Bending and free vibration analyses of functionally graded material nanoplates via a novel nonlocal single variable shear deformation plate theory. Proc Instit Mech Eng Part C 0954406220964522

  23. Hong C-C (2017) Thermal vibration of laminated magnetostrictive plates without shear effects. Int J Electr Compon Energy Convers 3(3):63

    Google Scholar 

  24. Hong CC (2010) Transient responses of magnetostrictive plates by using the GDQ method. Eur J Mech A Solids 29(6):1015–1021

    MATH  Google Scholar 

  25. Hosseini-Hashemi S, Rokni Damavandi Taher H, Akhavan H, Omidi M (2010) Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Appl Math Model 34(5):1276–1291

    MathSciNet  MATH  Google Scholar 

  26. Jha DK, Kant T, Singh RK (2012) Higher order shear and normal deformation theory for natural frequency of functionally graded rectangular plates. Nucl Eng Des 250:8–13

    Google Scholar 

  27. Karami B, Shahsavari D (2020) On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comput Methods Appl Mech Eng 359:767

    MathSciNet  MATH  Google Scholar 

  28. Keshtegar B, Farrokhian A, Kolahchi R, Trung N-T (2020) Dynamic stability response of truncated nanocomposite conical shell with magnetostrictive face sheets utilizing higher order theory of sandwich panels. Eur J MechA 82:104010

    MathSciNet  MATH  Google Scholar 

  29. Khani Arani H, Shariyat M, Mohammadian A (2020) Vibration analysis of magnetostrictive nano-plate by using modified couple stress and nonlocal elasticity theories. Int J Mater Metall Eng 14(9):229–234

    Google Scholar 

  30. Li Q, Xie B, Sahmani S, Safaei B (2020) Surface stress effect on the nonlinear free vibrations of functionally graded composite nanoshells in the presence of modal interaction. J Braz Soc Mech Sci Eng 42(5):237

    Google Scholar 

  31. Mahinzare M, Akhavan H, Ghadiri M (2020) A nonlocal strain gradient theory for rotating thermo-mechanical characteristics on magnetically actuated viscoelastic functionally graded nanoshell. J Intell Mater Syst Struct 31(12):1511–1523

    Google Scholar 

  32. Matsunaga H (2008) Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos Struct 82(4):499–512

    Google Scholar 

  33. Mindlin RD (1951) Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J Appl Mech 18:31–38

    MATH  Google Scholar 

  34. Phung-Van P, Ferreira AJM, Thai CH (2020) Computational optimization for porosity-dependent isogeometric analysis of functionally graded sandwich nanoplates. Compos Struct 239:112029

    Google Scholar 

  35. Pradhan SC, Ng TY, Lam KY, Reddy JN (2001) Control of laminated composite plates using magnetostrictive layers. Smart Mater Struct 10(4):657–667

    Google Scholar 

  36. Rao SS (2019) Vibration of continuous systems. Wiley, New Jersey

    Google Scholar 

  37. Reddy JN (2000) Analysis of functionally graded plates. Int J Numer Meth Eng 47(1–3):663–684

    MATH  Google Scholar 

  38. Reddy JN, Wang CM, Kitipornchai S (1999) Axisymmetric bending of functionally graded circular and annular plates. Eur J Mech A Solids 18(2):185–199

    MATH  Google Scholar 

  39. Reissner E (1976) On the theory of transverse bending of elastic plates. Int J Solids Struct 12(8):545–554

    MathSciNet  MATH  Google Scholar 

  40. Rezaei AS, Saidi AR (2015) Exact solution for free vibration of thick rectangular plates made of porous materials. Compos Struct 134:1051–1060

    Google Scholar 

  41. Sari MES, Al-Kouz WG, Atieh AM (2020) Transverse vibration of functionally graded tapered double nanobeams resting on elastic foundation. Appl Sci 10(2):493

    Google Scholar 

  42. Salehipour H, Shahgholian-Ghahfarokhi D, Shahsavar A, Civalek O, Edalati M (2020) Static deflection and free vibration analysis of functionally graded and porous cylindrical micro/nano shells based on the three-dimensional elasticity and modified couple stress theories. Mech Based Des Struct Mach 1–22

  43. Santapuri S, Scheidler JJ, Dapino MJ (2015) Two-dimensional dynamic model for composite laminates with embedded magnetostrictive materials. Compos Struct 132:737–745

    Google Scholar 

  44. Thai CH, Ferreira AJM, Phung-Van P (2020) A nonlocal strain gradient isogeometric model for free vibration and bending analyses of functionally graded plates. Compos Struct 251:634

    Google Scholar 

  45. Tran V-K, Pham Q-H, Nguyen-Thoi T (2020) A finite element formulation using four-unknown incorporating nonlocal theory for bending and free vibration analysis of functionally graded nanoplates resting on elastic medium foundations. Eng Comput. https://doi.org/10.1007/s00366-020-01107-7

    Article  Google Scholar 

  46. Yuan Y, Zhao X, Zhao Y, Sahmani S, Safaei B (2021) Dynamic stability of nonlocal strain gradient FGM truncated conical microshells integrated with magnetostrictive facesheets resting on a nonlinear viscoelastic foundation. Thin-Walled Struct 159:107249

    Google Scholar 

  47. Zenkour AM, El-Shahrany HD (2020) Control of a laminated composite plate resting on Pasternak’s foundations using magnetostrictive layers. Arch Appl Mech 90(9):1943–1959

    Google Scholar 

  48. Zenkour AM, El-Shahrany HD (2021) Hygrothermal vibration of adaptive composite magnetostrictive laminates supported by elastic substrate medium. Eur J Mech-A 85:104140

    MathSciNet  MATH  Google Scholar 

  49. Zenkour AM, El-Shahrany HD (2021) Quasi-3D theory for the vibration of a magnetostrictive laminated plate on elastic medium with viscoelastic core and faces. Compos Struct 257:113091

    Google Scholar 

  50. Zhao X, Lee YY, Liew KM (2009) Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J Sound Vib 319(3):918–939

    Google Scholar 

  51. Zhu C, Fang X, Liu J, Nie G, Zhang C (2020) An analytical solution for nonlinear vibration control of sandwich shallow doubly-curved nanoshells with functionally graded piezoelectric nanocomposite sensors and actuators. Mech Based Des Struct Mach 1–27

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahimi & Mehrdad Farajzadeh Ahari

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mehrdad Farajzadeh Ahari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest in preparing this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix 1

Appendix 1

$$K_{11} = - A_{11} \left( {\alpha^{2} } \right) - A_{66} \left( {\beta^{2} } \right)\,\,K_{12} = - A_{12} \left( {\alpha \beta } \right) - A_{66} \left( {\alpha \beta } \right)$$
$$K_{13} = 0\,\,K_{14} = - B_{11} \left( {\alpha^{2} } \right) - B_{66} \left( {\beta^{2} } \right)$$
$$K_{15} = - B_{12} \left( {\alpha \beta } \right) - B_{66} \left( {\alpha \beta } \right)$$
$$K_{21} = - A_{21} \left( {\alpha \beta } \right) - A_{66} \left( {\alpha \beta } \right)\,\,K_{22} = - A_{22} \left( {\alpha^{2} } \right) - A_{66} \left( {\beta^{2} } \right)$$
$$K_{23} = 0\,\,K_{24} = - B_{21} \left( {\alpha \beta } \right) - B_{66} \left( {\alpha \beta } \right)$$
$$K_{25} = - B_{22} \left( {\alpha^{2} } \right) - B_{66} \left( {\beta^{2} } \right)$$
$$K_{31} = 0\,\,K_{32} = 0$$
$$K_{33} = - A_{55} \left( {\alpha^{2} } \right) - A_{44} \left( {\beta^{2} } \right) - K_{w} - K_{g} \left( {\alpha^{2} } \right) - K_{g} \left( {\beta^{2} } \right) - K_{w} \left( {\mu^{2} \alpha^{2} } \right) - K_{w} \left( {\mu^{2} \beta^{2} } \right) - K_{g} \left( {\mu^{2} \alpha^{4} } \right) - K_{g} \left( {\mu^{2} \beta^{4} } \right) - 2K_{g} \left( {\mu^{2} \alpha^{2} \beta^{2} } \right)$$
$$K_{34} = - A_{55} \left( \alpha \right)\,\,K_{35} = - A_{44} \left( \beta \right)$$
$$K_{41} = - B_{11} \left( {\alpha^{2} } \right) - B_{66} \left( {\beta^{2} } \right)\,\,K_{42} = - B_{21} \left( {\alpha \beta } \right) - B_{66} \left( {\alpha \beta } \right)$$
$$K_{43} = - A_{55} \left( \alpha \right)\,\,K_{44} = - D_{11} \left( {\alpha^{2} } \right) - D_{66} \left( {\beta^{2} } \right) - A_{55}$$
$$K_{45} = - D_{12} \left( {\alpha \beta } \right) - D_{66} \left( {\alpha \beta } \right)$$
$$K_{51} = - B_{12} \left( {\alpha \beta } \right) - B_{66} \left( {\alpha \beta } \right)\,\,K_{52} = - B_{22} \left( {\alpha^{2} } \right) - B_{66} \left( {\beta^{2} } \right)$$
$$K_{53} = - A_{44} \left( \beta \right)\,\,K_{54} = - D_{12} \left( {\alpha \beta } \right) - D_{66} \left( {\alpha \beta } \right)$$
$$K_{55} = - D_{22} \left( {\beta^{2} } \right) - D_{66} \left( {\alpha^{2} } \right) - A_{44}$$
$$M_{11} = I_{0} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)\,\,M_{14} = I_{1} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)$$
$$M_{22} = I_{0} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)\,\,M_{25} = I_{1} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)$$
$$M_{33} = I_{0} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)\,\,M_{41} = I_{1} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)$$
$$M_{44} = I_{2} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)\,\,M_{52} = I_{1} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)$$
$$M_{55} = I_{2} \left( {1 + \mu^{2} \alpha^{2} + \mu^{2} \beta^{2} } \right)$$
$$C_{11} = C_{12} = C_{14} = C_{15} = 0\,\,C_{13} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} e_{31} \left( \alpha \right)K_{c} C\left( t \right)dz$$
$$C_{21} = C_{22} = C_{24} = C_{25} = 0\,\,C_{23} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} e_{32} \left( \beta \right)K_{c} C\left( t \right)dz$$
$$C_{31} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} e_{31} \left( \alpha \right)K_{c} C\left( t \right)dz\,\,C_{32} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} e_{31} \left( \beta \right)K_{c} C\left( t \right)dz$$
$$C_{33} = 0\,\,C_{34} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} ze_{31} \left( \alpha \right)K_{c} C\left( t \right)dz$$
$$C_{35} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} ze_{32} \left( \beta \right)K_{c} C\left( t \right)dz$$
$$C_{41} = C_{42} = C_{44} = C_{45} = 0\,\,C_{43} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} ze_{31} \left( \alpha \right)K_{c} C\left( t \right)dz$$
$$C_{51} = C_{52} = C_{54} = C_{55} = 0\,\,C_{53} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} ze_{32} \left( \beta \right)K_{c} C\left( t \right)dz$$
$$A_{11} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{11}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{11}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{11}^{f} dz$$
$$A_{12} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{12}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{12}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{12}^{f} dz$$
$$A_{22} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{22}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{22}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{22}^{f} dz$$
$$A_{44} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{44}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{44}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{44}^{f} dz$$
$$A_{55} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{55}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{55}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{55}^{f} dz$$
$$A_{66} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{66}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} C_{66}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{66}^{f} dz$$
$$B_{11} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{11}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{11}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{11}^{f} dz$$
$$B_{12} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{12}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{12}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{12}^{f} dz$$
$$B_{22} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{22}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{22}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{22}^{f} dz$$
$$B_{44} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{44}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{44}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{44}^{f} dz$$
$$B_{55} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{55}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{22}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{55}^{f} dz$$
$$B_{66} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{66}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} zC_{66}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{66}^{f} dz$$
$$D_{11} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{11}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{11}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{11}^{f} dz$$
$$D_{12} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{12}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{12}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{12}^{f} dz$$
$$D_{22} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{22}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{22}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{22}^{f} dz$$
$$D_{44} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{44}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{44}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{44}^{f} dz$$
$$D_{55} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{55}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{55}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{55}^{f} dz$$
$$D_{66} = \mathop \int \limits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{66}^{c} dz + \mathop \int \limits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{ - hc}{2}}} z^{2} C_{66}^{f} dz + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{66}^{f} dz$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Ahari, M.F. Magnetostriction-assisted active control of the multi-layered nanoplates: effect of the porous functionally graded facesheets on the system’s behavior. Engineering with Computers 39, 269–283 (2023). https://doi.org/10.1007/s00366-021-01539-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01539-9

Keywords

Search

Navigation