Skip to main content
SpringerLink
Log in

Computer simulation via a couple of homotopy perturbation methods and the generalized differential quadrature method for nonlinear vibration of functionally graded non-uniform micro-tube

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

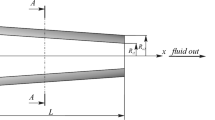
In this paper, to improve the vibrational response of microstructures, the impact of the nonlinear modal analysis of axially functionally graded (AFG) truncated conical micro-scale tube including the thermal loading for the different type of cross sections such as uniform section, linear tapered section, convex section, the exponential section are studied that are applicable for various application, for example, the micro-thermal fins, macro-/micro-fluid-flow diffuser, fluid-flow nozzle, fluid-flow throat, micro-sensor, etc. The nonlinear equations are obtained applying Hamilton’s principles based on the modified couple stress to determine the size effect and Euler–Bernoulli beam theory considering the von-Kármán’s nonlinear strain. The material combination varies along the tube’s length, denouncing the AFG tube made by metal and ceramic phases. The nonlinear equations are solved by applying a couple of homotopy perturbation methods (HPM) to calculating the nonlinear results and the generalized differential quadrature method (GDQM) to providing the initial conditions. The linear and nonlinear results presented the effect of various cross sections and other parameters on the micro-tube frequency that are valuable to design and manufacture the micro-electro-mechanical systems (MEMS).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Rajasekaran S (2018) Analysis of axially functionally graded nano-tapered Timoshenko beams by element-based Bernstein pseudospectral collocation (EBBPC). Eng Comput 34:543–563

    Google Scholar 

  2. Karami B, Janghorban M, Tounsi A (2019) Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng Comput 35:1297–1316

    Google Scholar 

  3. Hamed MA, Abo-bakr RM, Mohamed SA, Eltaher MA (2020) Influence of axial load function and optimization on static stability of sandwich functionally graded beams with porous core. Eng Comput 36:1929–1946

    Google Scholar 

  4. Mehditabar A, Rahimi GH (2021) Multiaxial ratcheting evaluation of functionally graded cylindrical shell by means of Ohno–Wang’s type models. Eng Comput 37:609–622

    Google Scholar 

  5. Ebrahimi F, Hosseini SHS (2021) Nonlinear vibration and dynamic instability analysis nanobeams under thermo-magneto-mechanical loads: a parametric excitation study. Eng Comput 37:395–408

    Google Scholar 

  6. Attia MA, Mohamed SA (2020) Thermal vibration characteristics of pre/post-buckled bi-directional functionally graded tapered microbeams based on modified couple stress Reddy beam theory. Eng Comput. https://doi.org/10.1007/s00366-020-01188-4

    Article  Google Scholar 

  7. Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2019) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput 37(2):921–936

    Google Scholar 

  8. Zhu X, Lu Z, Wang Z, Xue L, Ebrahimi-Mamaghani A (2020) Vibration of spinning functionally graded nanotubes conveying fluid. Eng Comput. https://doi.org/10.1007/s00366-020-01123-7

    Article  Google Scholar 

  9. Khiloun M, Bousahla AA, Kaci A, Bessaim A, Tounsi A, Mahmoud SR (2020) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Eng Comput 36:807–821

    Google Scholar 

  10. Zine A, Bousahla Abdelmoumen A, Bourada F, Benrahou Kouider H, Tounsi A, Adda Bedia EA et al (2020) Bending analysis of functionally graded porous plates via a refined shear deformation theory. Comput Concr 26:63–74

    Google Scholar 

  11. Bendenia N, Zidour M, Bousahla Abdelmoumen A, Bourada F, Tounsi A, Benrahou Kouider H et al (2020) Deflections, stresses and free vibration studies of FG-CNT reinforced sandwich plates resting on Pasternak elastic foundation. Comput Concr 26:213–226

    Google Scholar 

  12. Menasria A, Kaci A, Bousahla Abdelmoumen A, Bourada F, Tounsi A, Benrahou Kouider H et al (2020) A four-unknown refined plate theory for dynamic analysis of FG-sandwich plates under various boundary conditions. Steel Compos Struct 36:355–367

    Google Scholar 

  13. Guellil M, Saidi H, Bourada F, Bousahla Abdelmoumen A, Tounsi A, Al-Zahrani Mesfer M et al (2021) Influences of porosity distributions and boundary conditions on mechanical bending response of functionally graded plates resting on Pasternak foundation. Steel Compos Struct 38:1–15

    Google Scholar 

  14. Rabhi M, Benrahou Kouider H, Kaci A, Houari Mohammed Sid A, Bourada F, Bousahla Abdelmoumen A et al (2020) A new innovative 3-unknowns HSDT for buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions. Geomech Eng 22:119–132

    Google Scholar 

  15. Hirane H, Belarbi M-O, Houari MSA, Tounsi A (2021) On the layerwise finite element formulation for static and free vibration analysis of functionally graded sandwich plates. Eng Comput. https://doi.org/10.1007/s00366-020-01250-1

    Article  Google Scholar 

  16. Bekkaye Tahar Hacen L, Fahsi B, Bousahla Abdelmoumen A, Bourada F, Tounsi A, Benrahou Kouider H et al (2020) Porosity-dependent mechanical behaviors of FG plate using refined trigonometric shear deformation theory. Comput Concrete 26:439–450

    Google Scholar 

  17. Cuong-Le T, Nguyen KD, Nguyen-Trong N, Khatir S, Nguyen-Xuan H, Abdel-Wahab M (2021) A three-dimensional solution for free vibration and buckling of annular plate, conical, cylinder and cylindrical shell of FG porous-cellular materials using IGA. Compos Struct 259:113216

    Google Scholar 

  18. Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39:2731–2743

    MATH  Google Scholar 

  19. Shariati A, Habibi M, Tounsi A, Safarpour H, Safa M (2020) Application of exact continuum size-dependent theory for stability and frequency analysis of a curved cantilevered microtubule by considering viscoelastic properties. Eng Comput. https://doi.org/10.1007/s00366-020-01024-9

    Article  Google Scholar 

  20. Thanh CL, Nguyen TN, Vu TH, Khatir S, Abdel WM (2020) A geometrically nonlinear size-dependent hypothesis for porous functionally graded micro-plate. Eng Comput. https://doi.org/10.1007/s00366-020-01154-0

    Article  Google Scholar 

  21. Alimirzaei S, Mohammadimehr M, Tounsi A (2019) Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM: MSGT electro-magneto-elastic bending, buckling and vibration solutions. Struct Eng Mech 71:485–502

    Google Scholar 

  22. Mohammadi-Alasti B, Rezazadeh G, Borgheei A-M, Minaei S, Habibifar R (2011) On the mechanical behavior of a functionally graded micro-beam subjected to a thermal moment and nonlinear electrostatic pressure. Compos Struct 93:1516–1525

    Google Scholar 

  23. Al-shujairi M, Mollamahmutoğlu Ç (2018) Dynamic stability of sandwich functionally graded micro-beam based on the nonlocal strain gradient theory with thermal effect. Compos Struct 201:1018–1030

    Google Scholar 

  24. Jia XL, Ke LL, Zhong XL, Sun Y, Yang J, Kitipornchai S (2018) Thermal-mechanical-electrical buckling behavior of functionally graded micro-beams based on modified couple stress theory. Compos Struct 202:625–634

    Google Scholar 

  25. Babaei A, Noorani M-RS, Ghanbari A (2017) Temperature-dependent free vibration analysis of functionally graded micro-beams based on the modified couple stress theory. Microsyst Technol 23:4599–4610

    Google Scholar 

  26. Nateghi A, Salamat-talab M (2013) Thermal effect on size dependent behavior of functionally graded microbeams based on modified couple stress theory. Compos Struct 96:97–110

    Google Scholar 

  27. Jia XL, Zhang SM, Ke LL, Yang J, Kitipornchai S (2014) Thermal effect on the pull-in instability of functionally graded micro-beams subjected to electrical actuation. Compos Struct 116:136–146

    Google Scholar 

  28. Su Z, Jin G, Wang L, Wang D (2018) Thermo-mechanical vibration analysis of size-dependent functionally graded micro-beams with general boundary conditions. Int J Appl Mech 10:1850088

    Google Scholar 

  29. Dehrouyeh-Semnani AM, Mostafaei H, Dehrouyeh M, Nikkhah-Bahrami M (2017) Thermal pre- and post-snap-through buckling of a geometrically imperfect doubly-clamped microbeam made of temperature-dependent functionally graded materials. Compos Struct 170:122–134

    MATH  Google Scholar 

  30. Bhattacharya S, Das D (2019) Free vibration analysis of bidirectional-functionally graded and double-tapered rotating micro-beam in thermal environment using modified couple stress theory. Compos Struct 215:471–492

    Google Scholar 

  31. Babaei H, Reza EM (2020) Size-dependent vibrations of thermally pre/post-buckled FG porous micro-tubes based on modified couple stress theory. Int J Mech Sci 180:105694

    Google Scholar 

  32. Babaei H, Eslami MR (2020) On nonlinear vibration and snap-through stability of porous FG curved micro-tubes using two-step perturbation technique. Compos Struct 247:112447

    Google Scholar 

  33. Wang Y, Xie K, Shi C, Fu T (2019) Nonlinear bending of axially functionally graded microbeams reinforced by graphene nanoplatelets in thermal environments. Mater Res Express 6:085615

    Google Scholar 

  34. Wang Y, Wu D (2016) Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astronaut 127:171–181

    Google Scholar 

  35. Mirjavadi SS, Mohasel Afshari B, Shafiei N, Rabby S, Kazemi M (2017) Effect of temperature and porosity on the vibration behavior of two-dimensional functionally graded micro-scale Timoshenko beam. J Vib Control 24:4211–4225

    MathSciNet  MATH  Google Scholar 

  36. Shafiei N, Mousavi A, Ghadiri M (2016) Vibration behavior of a rotating non-uniform FG microbeam based on the modified couple stress theory and GDQEM. Compos Struct 149:157–169

    Google Scholar 

  37. Rajasekaran S, Khaniki HB (2019) Size-dependent forced vibration of non-uniform bi-directional functionally graded beams embedded in variable elastic environment carrying a moving harmonic mass. Appl Math Model 72:129–154

    MathSciNet  MATH  Google Scholar 

  38. Akgöz B, Civalek Ö (2013) Free vibration analysis of axially functionally graded tapered Bernoulli-Euler microbeams based on the modified couple stress theory. Compos Struct 98:314–322

    Google Scholar 

  39. Shafiei N, Kazemi M, Safi M, Ghadiri M (2016) Nonlinear vibration of axially functionally graded non-uniform nanobeams. Int J Eng Sci 106:77–94

    Google Scholar 

  40. Shafiei N, Kazemi M, Ghadiri M (2016) Nonlinear vibration of axially functionally graded tapered microbeams. Int J Eng Sci 102:12–26

    MathSciNet  MATH  Google Scholar 

  41. Ghayesh MH (2018) Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl Math Model 59:583–596

    MathSciNet  MATH  Google Scholar 

  42. Khaniki HB, Rajasekaran S (2018) Mechanical analysis of non-uniform bi-directional functionally graded intelligent micro-beams using modified couple stress theory. Mater Res Express 5:055703

    Google Scholar 

  43. Shafiei N, Mousavi A, Ghadiri M (2016) On size-dependent nonlinear vibration of porous and imperfect functionally graded tapered microbeams. Int J Eng Sci 106:42–56

    MATH  Google Scholar 

  44. Rajasekaran S, Khaniki HB (2017) Bending, buckling and vibration of small-scale tapered beams. Int J Eng Sci 120:172–188

    MathSciNet  MATH  Google Scholar 

  45. Hatami M, Ganji DD (2013) Thermal performance of circular convective–radiative porous fins with different section shapes and materials. Energy Convers Manage 76:185–193

    Google Scholar 

  46. Touloukian YS (1966) Thermophysical properties of high temperature solid materials. Volume 6. Intermetallics, Cermets, Polymers, and Composite Systems. Part 2. Cermets, Polymers, Composite Systems. Thermophysical and electronic properties information analysis center lafayette

  47. Reddy JN, Chin CD (1998) Thermomechanical analysis of functionally graded cylinders and plates. J Therm Stresses 21:593–626

    Google Scholar 

  48. Shafiei N, She G-L (2018) On vibration of functionally graded nano-tubes in the thermal environment. Int J Eng Sci 133:84–98

    MathSciNet  MATH  Google Scholar 

  49. Oyarhossein MA, Alizadeh AA, Habibi M, Makkiabadi M, Daman M, Safarpour H et al (2020) Dynamic response of the nonlocal strain-stress gradient in laminated polymer composites microtubes. Sci Rep 10:1–19

    Google Scholar 

  50. Shariati A, Ghabussi A, Habibi M, Safarpour H, Safarpour M, Tounsi A et al (2020) Extremely large oscillation and nonlinear frequency of a multi-scale hybrid disk resting on nonlinear elastic foundation. Thin-Walled Struct 154:106840

    Google Scholar 

  51. Ghabussi A, Habibi M, NoormohammadiArani O, Shavalipour A, Moayedi H, Safarpour H (2020) Frequency characteristics of a viscoelastic graphene nanoplatelet–reinforced composite circular microplate. J Vib Control 27:101–118

    MathSciNet  Google Scholar 

  52. Safarpour M, Ghabussi A, Ebrahimi F, Habibi M, Safarpour H (2020) Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin-Walled Struct 150:106683

    Google Scholar 

  53. Ghabussi A, Asgari Marnani J, Rohanimanesh MS (2021) Seismic performance assessment of a novel ductile steel braced frame equipped with steel curved damper. Structures 31:87–97

    Google Scholar 

  54. Shariati A, Jung DW, Mohammad-Sedighi H, Żur KK, Habibi M, Safa M (2020) Stability and dynamics of viscoelastic moving Rayleigh beams with an asymmetrical distribution of material parameters. Symmetry 12:586

    Google Scholar 

  55. Moayedi H, Darabi R, Ghabussi A, Habibi M, Foong LK (2020) Weld orientation effects on the formability of tailor welded thin steel sheets. Thin-Walled Struct 149:106669

    Google Scholar 

  56. Li J, Tang F, Habibi M (2020) Bi-directional thermal buckling and resonance frequency characteristics of a GNP-reinforced composite nanostructure. Eng Comput. https://doi.org/10.1007/s00366-020-01110-y

  57. Al-Furjan MSH, Habibi M, Ni J, Jung Dw, Tounsi A (2020) Frequency simulation of viscoelastic multi-phase reinforced fully symmetric systems. Eng Comput. https://doi.org/10.1007/s00366-020-01200-x

  58. Li Y, Li S, Guo K, Fang X, Habibi M (2020) On the modeling of bending responses of graphene-reinforced higher order annular plate via two-dimensional continuum mechanics approach. Eng Comput. https://doi.org/10.1007/s00366-020-01166-w

  59. Bai Y, Alzahrani B, Baharom S, Habibi M (2020) Semi-numerical simulation for vibrational responses of the viscoelastic imperfect annular system with honeycomb core under residual pressure. Eng Comput. https://doi.org/10.1007/s00366-020-01191-9

  60. Al-Furjan MSH, Habibi M, rahimi A, Chen G, Safarpour H, Safarpour M, et al (2020) Chaotic simulation of the multi-phase reinforced thermo-elastic disk using GDQM. Eng Comput. https://doi.org/10.1007/s00366-020-01144-2

  61. Al-Furjan MSH, Safarpour H, Habibi M, Safarpour M, Tounsi A (2020) A comprehensive computational approach for nonlinear thermal instability of the electrically FG-GPLRC disk based on GDQ method. Eng Comput. https://doi.org/10.1007/s00366-020-01088-7

    Article  Google Scholar 

  62. Al-Furjan MSH, Habibi M, Ghabussi A, Safarpour H, Safarpour M, Tounsi A (2021) Non-polynomial framework for stress and strain response of the FG-GPLRC disk using three-dimensional refined higher-order theory. Eng Struct 228:111496

    Google Scholar 

  63. Al-Furjan MSH, Hatami A, Habibi M, Shan L, Tounsi A (2021) On the vibrations of the imperfect sandwich higher-order disk with a lactic core using generalize differential quadrature method. Compos Struct 257:113150

    Google Scholar 

  64. Shafiei N, Kazemi M, Ghadiri M (2015) On size-dependent vibration of rotary axially functionally graded microbeam. Int J Eng Sci. https://doi.org/10.1016/j.ijengsci.2015.12.008

    Article  Google Scholar 

  65. Ghadiri M, Shafiei N (2015) Nonlinear bending vibration of a rotating nanobeam based on nonlocal Eringen’s theory using differential quadrature method. Microsyst Technol. https://doi.org/10.1007/s00542-015-2662-9

    Article  Google Scholar 

  66. Shafiei N, Kazemi M, Ghadiri M (2016) Nonlinear vibration of axially functionally graded tapered microbeams. Int J Eng Sci. https://doi.org/10.1016/j.ijengsci.2016.02.007

    Article  MathSciNet  MATH  Google Scholar 

  67. He J-H (2002) Modified Lindstedt-Poincare methods for some strongly non-linear oscillations: Part I: expansion of a constant. Int J Non-Linear Mech 37:309–314

    MATH  Google Scholar 

  68. He J-H (2002) Modified Lindstedt-Poincare methods for some strongly non-linear oscillations: Part II: a new transformation. Int J Non-Linear Mech 37:315–320

    MATH  Google Scholar 

  69. Wang C, Zhang Y, He X (2007) Vibration of nonlocal Timoshenko beams. Nanotechnology 18:105401

    Google Scholar 

  70. Malekzadeh P, Shojaee M (2013) Surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams. Compos B Eng 52:84–92

    Google Scholar 

  71. Lestari W, Hanagud S (2001) Nonlinear vibration of buckled beams: some exact solutions. Int J Solids Struct 38:4741–4757

    MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the Research team project of Nanning University (2018KYTD03), the first-class professional Breeding Project of Nanning University (2020YLZYPY03).

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Nanning University, Nanning, 530200, Guangxi, China

    Xiaoping Huang

  2. Department of Intelligent Manufacturing, Nanning College for Vocational Technology, Nanning, 530008, Guangxi, China

    Yemao Zhang

  3. Faculty of Engineering and Technology, Department of Electrical Engineering, Imam Khomeini International University, 34149-16818, Qazvin, Iran

    Zohre Moradi

  4. Hoonam Sanat Farnak Engineering and Technology Company, Ilam, Iran

    Navvab Shafiei

Authors
  1. Xiaoping Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yemao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zohre Moradi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Navvab Shafiei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yemao Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, X., Zhang, Y., Moradi, Z. et al. Computer simulation via a couple of homotopy perturbation methods and the generalized differential quadrature method for nonlinear vibration of functionally graded non-uniform micro-tube. Engineering with Computers 38 (Suppl 3), 2481–2498 (2022). https://doi.org/10.1007/s00366-021-01395-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01395-7

Keywords

Search

Navigation