Skip to main content
SpringerLink
Log in

Dynamic response of double-FG porous beam system subjected to moving load

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

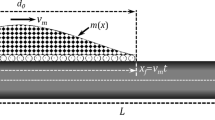
In this paper, the vibration response of the double-FG porous beam system (DFGPBS) acted by a moving load is investigated. The DFGPBS composed of two parallel FG porous beams with their material properties varying along both the axial and transverse directions, i.e., bi-directional FG material distribution, is taken into account. The porous imperfection is simulated by distributing the porosity along the beam thickness with even and uneven patterns. The governing equations of this bi-directional DFGPBS under a moving load are established with the aid of the Hamilton principle associated with the Timoshenko beam theory. The Ritz method is adopted to discrete the differential governing equations, which are solved by the Newmark-β approach. The validation of the present model is performed by comparing the numerical results with two previous works. Then, the parametric study is carried out to investigate the influences of bi-directional gradient indices, porosity volume fraction, boundary conditions, stiffness of elastic layer, and velocity of the moving load on the vibration response of bi-directional DFGPBSs excited by a moving load. It is demonstrated that the vibration response of the double-beam system subjected to moving loads can be governed by tailoring the distribution of the bi-directional FG materials. The present work can be used to guide the multi-functional design of a double-beam system under dynamic loadings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. Liu H, Zhang Q, Yang X, Ma J (2021) Size-dependent vibration of laminated composite nanoplate with piezo-magnetic face sheets. Eng Comput. https://doi.org/10.1007/s00366-021-01285-y

    Article  Google Scholar 

  2. Tagrara SH, Benachour A, Bouiadjra MB, Tounsi A (2015) On bending, buckling and vibration responses of functionally graded carbon nanotube-reinforced composite beams. Steel Compos Struct 19:1259–1277

    Google Scholar 

  3. Gul U, Aydogdu M, Karacam F (2019) Dynamics of a functionally graded Timoshenko beam considering new spectrums. Compos Struct 207:273–291

    Google Scholar 

  4. Liu H, Wu H, Lyu Z (2020) Nonlinear resonance of FG multilayer beam-type nanocomposites: effects of graphene nanoplatelet-reinforcement and geometric imperfection. Aerosp Sci Technol 98:105702

    Google Scholar 

  5. Wu Q, Chen H, Gao W (2019) Nonlocal strain gradient forced vibrations of FG-GPLRC nanocomposite microbeams. Eng Comput 36:1739–1750

    Google Scholar 

  6. Wu H, Liu H (2020) Nonlinear thermo-mechanical response of temperature-dependent FG sandwich nanobeams with geometric imperfection. Eng Comput. https://doi.org/10.1007/s00366-020-01005-y

    Article  Google Scholar 

  7. Liu H, Lv Z, Wu H (2019) Nonlinear free vibration of geometrically imperfect functionally graded sandwich nanobeams based on nonlocal strain gradient theory. Compos Struct 214:47–61

    Google Scholar 

  8. Moita JS, Araújo AL, Correia VF, Mota Soares CM, Herskovits J (2020) Buckling behavior of composite and functionally graded material plates. Eur J Mech A Solids 80:103921

    MathSciNet  MATH  Google Scholar 

  9. Zhao J, Zhang Y, Choe K, Qu X, Wang A, Wang Q (2019) Three-dimensional exact solution for the free vibration of thick functionally graded annular sector plates with arbitrary boundary conditions. Compos B Eng 159:418–436

    Google Scholar 

  10. Zafarmand H, Kadkhodayan M (2019) Nonlinear material and geometric analysis of thick functionally graded plates with nonlinear strain hardening using nonlinear finite element method. Aerosp Sci Technol 92:930–944

    Google Scholar 

  11. Ansari R, Hasrati E, Torabi J (2020) Effect of external pressure on the vibration analysis of higher order shear deformable FG-CNTRC spherical panels. Eng Comput. https://doi.org/10.1007/s00366-020-01138-0

    Article  Google Scholar 

  12. Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2019) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput. https://doi.org/10.1007/s00366-019-00864-4

    Article  Google Scholar 

  13. Liu B, Guo M, Liu C, Xing Y (2019) Free vibration of functionally graded sandwich shallow shells in thermal environments by a differential quadrature hierarchical finite element method. Compos Struct 225:111173

    Google Scholar 

  14. Shakouri M (2019) Free vibration analysis of functionally graded rotating conical shells in thermal environment. Compos B Eng 163:574–584

    Google Scholar 

  15. Vaishali MT, Karsh PK, Basu B, Dey S (2020) Machine learning based stochastic dynamic analysis of functionally graded shells. Compos Struct 237:111870

    Google Scholar 

  16. Ahmadi H (2018) Nonlinear primary resonance of imperfect spiral stiffened functionally graded cylindrical shells surrounded by damping and nonlinear elastic foundation. Eng Comput 35:1491–1505

    Google Scholar 

  17. Huang Y, Li X-F (2010) A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. J Sound Vib 329:2291–2303

    Google Scholar 

  18. Zhang X, Ye Z, Zhou Y (2019) A Jacobi polynomial based approximation for free vibration analysis of axially functionally graded material beams. Compos Struct 225:111070

    Google Scholar 

  19. Kumar S, Mitra A, Roy H (2017) Forced vibration response of axially functionally graded non-uniform plates considering geometric nonlinearity. Int J Mech Sci 128–129:194–205

    Google Scholar 

  20. Han H, Cao D, Liu L (2019) A new approach for steady-state dynamic response of axially functionally graded and non-uniformed beams. Compos Struct 226:111270

    Google Scholar 

  21. Ebrahimi-Mamaghani A, Sarparast H, Rezaei M (2020) On the vibrations of axially graded Rayleigh beams under a moving load. Appl Math Model 84:554–570

    MathSciNet  MATH  Google Scholar 

  22. Sınır S, Çevik M, Sınır BG (2018) Nonlinear free and forced vibration analyses of axially functionally graded Euler-Bernoulli beams with non-uniform cross-section. Compos B Eng 148:123–131

    Google Scholar 

  23. Chen X, Lu Y, Li Y (2019) Free vibration, buckling and dynamic stability of bi-directional FG microbeam with a variable length scale parameter embedded in elastic medium. Appl Math Model 67:430–448

    MathSciNet  MATH  Google Scholar 

  24. Truong TT, Lee S, Lee J (2020) An artificial neural network-differential evolution approach for optimization of bidirectional functionally graded beams. Compos Struct 233:111517

    Google Scholar 

  25. Rajasekaran S, Khaniki HB (2019) Size-dependent forced vibration of non-uniform bi-directional functionally graded beams embedded in variable elastic environment carrying a moving harmonic mass. Appl Math Model 72:129–154

    MathSciNet  MATH  Google Scholar 

  26. Nguyen DK, Nguyen QH, Tran TT, Bui VT (2016) Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech 228:141–155

    MathSciNet  MATH  Google Scholar 

  27. Lei J, He Y, Li Z, Guo S, Liu D (2019) Postbuckling analysis of bi-directional functionally graded imperfect beams based on a novel third-order shear deformation theory. Compos Struct 209:811–829

    Google Scholar 

  28. Tang Y, Ding Q (2019) Nonlinear vibration analysis of a bi-directional functionally graded beam under hygro-thermal loads. Compos Struct 225:111076

    Google Scholar 

  29. Tang Y, Lv X, Yang T (2019) Bi-directional functionally graded beams: asymmetric modes and nonlinear free vibration. Compos B Eng 156:319–331

    Google Scholar 

  30. Gao K, Li R, Yang J (2019) Dynamic characteristics of functionally graded porous beams with interval material properties. Eng Struct 197:109441

    Google Scholar 

  31. Ebrahimi F, Zia M (2015) Large amplitude nonlinear vibration analysis of functionally graded Timoshenko beams with porosities. Acta Astron 116:117–125

    Google Scholar 

  32. Fouaidi M, Jamal M, Belouaggadia N (2020) Nonlinear bending analysis of functionally graded porous beams using the multiquadric radial basis functions and a Taylor series-based continuation procedure. Compos Struct 252:112593

    Google Scholar 

  33. Chen D, Zheng S, Wang Y, Yang L, Li Z (2020) Nonlinear free vibration analysis of a rotating two-dimensional functionally graded porous micro-beam using isogeometric analysis. Eur J Mech A Solids 84:104083

    MathSciNet  MATH  Google Scholar 

  34. Akbaş ŞD (2018) Forced vibration analysis of functionally graded porous deep beams. Compos Struct 186:293–302

    Google Scholar 

  35. Sahmani S, Fattahi AM, Ahmed NA (2019) Develop a refined truncated cubic lattice structure for nonlinear large-amplitude vibrations of micro/nano-beams made of nanoporous materials. Eng Comput 36:359–375

    Google Scholar 

  36. Zhang Q, Liu H (2020) On the dynamic response of porous functionally graded microbeam under moving load. Int J Eng Sci 153:103317

    MathSciNet  MATH  Google Scholar 

  37. Liu H, Liu H, Yang J (2018) Vibration of FG magneto-electro-viscoelastic porous nanobeams on visco-Pasternak foundation. Compos B Eng 155:244–256

    Google Scholar 

  38. Trinh M-C, Nguyen D-D, Kim S-E (2019) Effects of porosity and thermomechanical loading on free vibration and nonlinear dynamic response of functionally graded sandwich shells with double curvature. Aerosp Sci Technol 87:119–132

    Google Scholar 

  39. Huang X-L, Dong L, Wei G-Z, Zhong D-Y (2019) Nonlinear free and forced vibrations of porous sigmoid functionally graded plates on nonlinear elastic foundations. Compos Struct 228:111326

    Google Scholar 

  40. Zhou K, Huang X, Tian J, Hua H (2018) Vibration and flutter analysis of supersonic porous functionally graded material plates with temperature gradient and resting on elastic foundation. Compos Struct 204:63–79

    Google Scholar 

  41. Allahkarami F, Ghassabzadeh Saryazdi M, Tohidi H (2020) Dynamic buckling analysis of bi-directional functionally graded porous truncated conical shell with different boundary conditions. Compos Struct 252:112680

    Google Scholar 

  42. Salehipour H, Shahsavar A, Civalek O (2019) Free vibration and static deflection analysis of functionally graded and porous micro/nanoshells with clamped and simply supported edges. Compos Struct 221:110842

    Google Scholar 

  43. Liu Y, Su S, Huang H, Liang Y (2019) Thermal-mechanical coupling buckling analysis of porous functionally graded sandwich beams based on physical neutral plane. Compos B Eng 168:236–242

    Google Scholar 

  44. Lo Feudo S, Touzé C, Boisson J, Cumunel G (2019) Nonlinear magnetic vibration absorber for passive control of a multi–storey structure. J Sound Vib 438:33–53

    Google Scholar 

  45. Hussein MFM, Hunt HEM (2006) Modelling of floating-slab tracks with continuous slabs under oscillating moving loads. J Sound Vib 297:37–54

    Google Scholar 

  46. Yankelevsky DZ (1991) Analysis of a composite layered elastic foundation. Int J Mech Sci 33:169–177

    MATH  Google Scholar 

  47. Zhao X, Chen B, Li YH, Zhu WD, Nkiegaing FJ, Shao YB (2020) Forced vibration analysis of Timoshenko double-beam system under compressive axial load by means of Green’s functions. J Sound Vib 464:115001

    Google Scholar 

  48. Machado SP, Febbo M, Ramírez JM, Gatti CD (2020) Rotational double-beam piezoelectric energy harvester impacting against a stop. J Sound Vib 469:115141

    Google Scholar 

  49. Fei H, Danhui D, Wei C, Jubao Z (2020) A novel analysis method for damping characteristic of a type of double-beam systems with viscoelastic layer. Appl Math Model 80:911–928

    MathSciNet  MATH  Google Scholar 

  50. Han F, Dan D, Cheng W (2018) An exact solution for dynamic analysis of a complex double-beam system. Compos Struct 193:295–305

    Google Scholar 

  51. Palmeri A, Adhikari S (2011) A Galerkin-type state-space approach for transverse vibrations of slender double-beam systems with viscoelastic inner layer. J Sound Vib 330:6372–6386

    Google Scholar 

  52. Deng H, Chen K, Cheng W, Zhao S (2017) Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler–Pasternak elastic foundation. Compos Struct 160:152–168

    Google Scholar 

  53. Rezaiee-Pajand M, Hozhabrossadati SM (2016) Analytical and numerical method for free vibration of double-axially functionally graded beams. Compos Struct 152:488–498

    Google Scholar 

  54. Wang Y, Zhu X, Lou Z (2019) Dynamic response of beams under moving loads with finite deformation. Nonlinear Dyn 98:167–184

    MATH  Google Scholar 

  55. Tabejieu LMA, Nbendjo BRN, Filatrella G, Woafo P (2017) Amplitude stochastic response of Rayleigh beams to randomly moving loads. Nonlinear Dyn 89:925–937

    Google Scholar 

  56. Sheng GG, Wang X (2017) The geometrically nonlinear dynamic responses of simply supported beams under moving loads. Appl Math Model 48:183–195

    MathSciNet  MATH  Google Scholar 

  57. Esen I (2020) Dynamics of size-dependant Timoshenko micro beams subjected to moving loads. Int J Mech Sci 175:105501

    Google Scholar 

  58. Gan BS, Kien ND, Ha LT (2018) Effect of intermediate elastic support on vibration of functionally graded Euler–Bernoulli beams excited by a moving point load. J Asian Archit Build Eng 16:363–369

    Google Scholar 

  59. Esen I (2019) Dynamic response of a functionally graded Timoshenko beam on two-parameter elastic foundations due to a variable velocity moving mass. Int J Mech Sci 153–154:21–35

    Google Scholar 

  60. Wang Y, Wu D (2016) Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astron 127:171–181

    Google Scholar 

  61. Liu S, Yang B (2019) A closed-form analytical solution method for vibration analysis of elastically connected double-beam systems. Compos Struct 212:598–608

    Google Scholar 

  62. Şimşek M, Cansız S (2012) Dynamics of elastically connected double-functionally graded beam systems with different boundary conditions under action of a moving harmonic load. Compos Struct 94:2861–2878

    Google Scholar 

  63. Karamanli A, Vo TP (2021) Bending, vibration, buckling analysis of bi-directional FG porous microbeams with a variable material length scale parameter. Appl Math Model 91:723–748

    MathSciNet  MATH  Google Scholar 

  64. Chen X, Lu Y, Zhu B, Zhang X, Li Y (2019) Nonlinear resonant behaviors of bi-directional functionally graded material microbeams: one-/two-parameter bifurcation analyses. Compos Struct 223:110896

    Google Scholar 

  65. Sahmani S, Safaei B (2019) Nonlocal strain gradient nonlinear resonance of bi-directional functionally graded composite micro/nano-beams under periodic soft excitation. Thin Walled Struct 143:106226

    Google Scholar 

  66. Liu H, Zhang Q, Ma J (2021) Thermo-mechanical dynamics of two-dimensional FG microbeam subjected to a moving harmonic load. Acta Astron 178:681–692

    Google Scholar 

  67. Xie K, Wang Y, Fan X, Fu T (2020) Nonlinear free vibration analysis of functionally graded beams by using different shear deformation theories. Appl Math Model 77:1860–1880

    MathSciNet  MATH  Google Scholar 

  68. Al Rjoub YS, Hamad AG (2016) Free vibration of functionally Euler-Bernoulli and Timoshenko graded porous beams using the transfer matrix method. KSCE J Civ Eng 21:792–806

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Solid Mechanics, School of Aeronautic Science and Engineering, Beihang University (BUAA), Beijing, 100191, China

    Shujia Chen & Qiao Zhang

  2. School of Mechanical and Aerospace Engineering, Nanyang Technological University (NTU), Singapore, 639798, Singapore

    Hu Liu

Authors
  1. Shujia Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qiao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hu Liu.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, S., Zhang, Q. & Liu, H. Dynamic response of double-FG porous beam system subjected to moving load. Engineering with Computers 38 (Suppl 3), 2309–2328 (2022). https://doi.org/10.1007/s00366-021-01376-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01376-w

Keywords

Search

Navigation