Couple stress-based dynamic stability analysis of functionally graded composite truncated conical microshells with magnetostrictive facesheets embedded within nonlinear viscoelastic foundations

Abstract

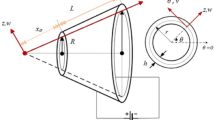
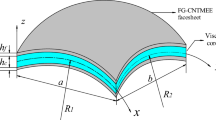
In this paper, size-dependent dynamic stability of axially loaded functionally graded (FG) composite truncated conical microshells with magnetostrictive facesheets surrounded by nonlinear viscoelastic foundations including a two-parameter Winkler–Pasternak medium augmented via a Kelvin–Voigt viscoelastic approach is analyzed considering nonlinear cubic stiffness. To this purpose, von Karman-type kinematic nonlinearity along with modified couple stress theory of elasticity was applied to third-order shear deformation conical shell theory in the presence of magnetic permeability tensor and magnetic fluxes. The numerical technique of generalized differential quadrature (GDQ) was used for the solution of microstructural-dependent dynamic stability responses of FG composite truncated conical microshells. It was seen that moving from prebuckling to postbuckling domain somehow increased the significance of couple stress type of size dependency on frequency. In addition, within both prebuckling and postbuckling regimes, an increase of material gradient index decreased the importance of couple stress type of size dependency on the frequency of an axially loaded FG composite truncated conical microshell. Furthermore, it was revealed that by applying a positive magnetic field to an axially loaded truncated conical microshell with magnetostrictive facesheets, its frequency at a specific axial load value was increased in prebuckling domain and decreased in postbuckling domain. However, this pattern was reversed by applying a negative magnetic field.

Appendices

Appendix 1

$$\frac{\partial {N}_{xx}^{*}}{\partial x}+\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial {N}_{x\theta }^{*}}{\partial \theta }+\frac{{N}_{xx}^{*}-{N}_{\theta \theta }^{*}}{x}+\frac{1}{4{x}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial {\mathcal{Q}}_{x}^{**}}{\partial \theta }+\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{Q}}_{x}^{**}}{\partial x\partial \theta }+\frac{1}{4{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{Q}}_{\theta }^{**}}{\partial {\theta }^{2}}={I}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}+{I}_{3}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}-\left({I}_{1}-{I}_{3}\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}},$$

$$\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial {N}_{\theta \theta }^{*}}{\partial \theta }+\frac{\partial {N}_{x\theta }^{*}}{\partial x}+2\frac{{N}_{x\theta }^{*}}{x}+\frac{{Q}_{\theta }^{*}}{x\mathrm{tan}\left(\alpha \right)}-\frac{1}{4}\frac{{\partial }^{2}{\mathcal{Q}}_{x}^{**}}{\partial {x}^{2}}-\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{Q}}_{\theta }^{**}}{\partial x\partial \theta }={I}_{0}\frac{{\partial }^{2}v}{\partial {t}^{2}}+\frac{{I}_{3}}{x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{3}w}{\partial \theta \partial {t}^{2}}-\left({I}_{1}-{I}_{3}\right)\frac{{\partial }^{2}{\psi }_{\theta }}{\partial {t}^{2}},$$

$$\frac{\partial {Q}_{x}^{*}}{\partial x}-\frac{\partial {P}_{x}^{*}}{\partial x}+\frac{1}{x\mathrm{sin}\left(\alpha \right)}\left(\frac{\partial {Q}_{\theta }^{*}}{\partial \theta }-\frac{\partial {P}_{\theta }^{*}}{\partial \theta }\right)+\frac{{Q}_{x}^{*}-{P}_{x}^{*}}{x}+\frac{{\partial }^{2}{R}_{xx}^{*}}{\partial {x}^{2}}+\frac{1}{{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}{R}_{\theta \theta }^{*}}{\partial {\theta }^{2}}-\frac{1}{x}\frac{\partial {R}_{\theta \theta }^{*}}{\partial x}+\frac{2}{x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}{R}_{x\theta }^{*}}{\partial x\partial \theta }+\frac{2}{{x}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial {R}_{x\theta }^{*}}{\partial \theta }-\frac{{N}_{\theta \theta }^{*}}{x\mathrm{tan}\left(\alpha \right)}-\frac{\partial }{\partial x}\left({N}_{xx}^{*}\frac{\partial w}{\partial x}+\frac{{N}_{x\theta }^{*}}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial w}{\partial \theta }\right)-\frac{\partial }{\partial \theta }\left(\frac{{N}_{\theta \theta }^{*}}{{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{\partial w}{\partial \theta }+\frac{{N}_{x\theta }^{*}}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial w}{\partial x}\right)-\frac{1}{2x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}\left({\mathcal{N}}_{xx}^{**}-{\mathcal{N}}_{\theta \theta }^{**}+{\mathcal{Y}}_{xx}^{**}-{\mathcal{Y}}_{\theta \theta }^{**}\right)}{\partial x\partial \theta }-\frac{1}{2{x}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial \left({\mathcal{N}}_{xx}^{**}+{\mathcal{Y}}_{xx}^{**}\right)}{\partial \theta }-\frac{1}{4{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}\left({N}_{x\theta }^{**}+{\mathcal{Y}}_{x\theta }^{**}\right)}{\partial {\theta }^{2}}+\frac{1}{4}\frac{{\partial }^{2}{\mathcal{Y}}_{x\theta }^{**}}{\partial {x}^{2}}+\frac{2}{x{h}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial {\mathcal{P}}_{x}^{**}}{\partial \theta }-\frac{2}{{h}^{2}}\frac{\partial {\mathcal{P}}_{\theta }^{**}}{\partial x}-\frac{1}{2x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{3}{\mathcal{T}}_{x}^{**}}{\partial {x}^{2}\partial \theta }-\frac{1}{2{x}^{3}\mathrm{sin}\left(\alpha \right)}\frac{\partial {\mathcal{T}}_{x}^{**}}{\partial \theta }-\frac{1}{2{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{3}{\mathcal{T}}_{\theta }^{**}}{\partial x\partial {\theta }^{2}}-\frac{1}{4{x}^{3}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{T}}_{\theta }^{**}}{\partial {\theta }^{2}}-{K}_{w}w+{K}_{s}\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{1}{{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}w}{\partial {\theta }^{2}}\right)+{K}_{nl}{w}^{3}+{N}_{xx}^{M}\frac{{\partial }^{2}w}{\partial {x}^{2}}+{N}_{\theta \theta }^{M}\frac{1}{{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}w}{\partial {\theta }^{2}}+P\frac{{\partial }^{2}w}{\partial {x}^{2}}=2{I}_{0}c\frac{\partial w}{\partial t}+{I}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-{I}_{6}\left(\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{1}{{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{4}w}{\partial {\theta }^{2}\partial {t}^{2}}\right)+{I}_{3}\left(\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}+\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{3}v}{\partial \theta \partial {t}^{2}}\right)+\left({I}_{4}-{I}_{6}\right)\left(\frac{{\partial }^{3}{\psi }_{x}}{\partial x\partial {t}^{2}}+\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{3}{\psi }_{\theta }}{\partial \theta \partial {t}^{2}}\right),$$

$$\frac{\partial \left({M}_{xx}^{*}-{R}_{xx}^{*}\right)}{\partial x}-\frac{\left({M}_{\theta \theta }^{*}-{R}_{\theta \theta }^{*}\right)}{x}+\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial \left({M}_{x\theta }^{*}-{R}_{x\theta }^{*}\right)}{\partial \theta }-{Q}_{x}^{*}+{P}_{x}^{*}+\frac{1}{2x\mathrm{sin}\left(\alpha \right)}\frac{\partial \left({\mathcal{N}}_{\theta \theta }^{**}+{\mathcal{Y}}_{\theta \theta }^{**}\right)}{\partial \theta }+\frac{1}{4}\frac{\partial {\mathcal{N}}_{x\theta }^{**}}{\partial x}-\frac{1}{4}\frac{\partial {\mathcal{Y}}_{x\theta }^{**}}{\partial x}+\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{P}}_{x}^{**}}{\partial x\partial \theta }+\frac{1}{4{x}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial {\mathcal{P}}_{x}^{**}}{\partial \theta }+\frac{2{\mathcal{P}}_{\theta }^{**}}{{h}^{2}}+\frac{1}{4{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{P}}_{\theta }^{**}}{\partial {\theta }^{2}}=\left({I}_{2}-{I}_{4}+{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{x}}{\partial {t}^{2}}+\left({I}_{6}-{I}_{4}\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}-\left({I}_{1}-{I}_{3}\right)\frac{{\partial }^{2}u}{\partial {t}^{2}},$$

$$\frac{1}{x\mathrm{sin}\left(\alpha \right)}\frac{\partial \left({{\varvec{M}}}_{{\varvec{\theta}}{\varvec{\theta}}}^{\boldsymbol{*}}-{{\varvec{R}}}_{{\varvec{\theta}}{\varvec{\theta}}}^{\boldsymbol{*}}\right)}{\partial \theta }+\frac{\partial \left({M}_{x\theta }^{*}-{R}_{x\theta }^{*}\right)}{\partial x}-\frac{\left({M}_{x\theta }^{*}-{R}_{x\theta }^{*}\right)}{x}-{Q}_{\theta }^{*}+{P}_{\theta }^{*}-\frac{1}{2}\frac{\partial \left({N}_{xx}^{**}-{\mathcal{Y}}_{xx}^{**}\right)}{\partial x}-\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{\partial \left({N}_{x\theta }^{**}-{\mathcal{Y}}_{x\theta }^{**}\right)}{\partial \theta }-\frac{2{\mathcal{P}}_{x}^{**}}{{h}^{2}}-\frac{1}{4}\frac{{\partial }^{2}{\mathcal{P}}_{x}^{**}}{\partial {x}^{2}}-\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{P}}_{\theta }^{**}}{\partial x\partial \theta }+\frac{1}{4}\frac{{\partial }^{2}{\mathcal{T}}_{x}^{**}}{\partial {x}^{2}}-\frac{1}{4x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{2}\left({\mathcal{T}}_{x}^{**}-{\mathcal{T}}_{\theta }^{**}\right)}{\partial x\partial \theta }+\frac{1}{4{x}^{2}\mathrm{sin}\left(\alpha \right)}\frac{\partial {\mathcal{T}}_{x}^{**}}{\partial \theta }-\frac{1}{4{x}^{2}{\mathrm{sin}}^{2}\left(\alpha \right)}\frac{{\partial }^{2}{\mathcal{T}}_{\theta }^{**}}{\partial {\theta }^{2}}=\left({I}_{2}-{I}_{4}+{I}_{6}\right)\frac{{\partial }^{2}{\psi }_{\theta }}{\partial {t}^{2}}+\frac{{I}_{6}-{I}_{4}}{x\mathrm{sin}\left(\alpha \right)}\frac{{\partial }^{3}w}{\partial \theta \partial {t}^{2}}-\left({I}_{1}-{I}_{3}\right)\frac{{\partial }^{2}v}{\partial {t}^{2}},$$

$${\int }_{-\frac{h}{2}}^\frac{h}{2}\left[\frac{\partial {\mathcal{B}}_{x}}{\partial x}\mathrm{cos}\left(\beta z\right)+\frac{\partial {\mathcal{B}}_{\theta }}{\partial \theta }\frac{\mathrm{cos}\left(\beta z\right)}{x\mathrm{sin}\left(\alpha \right)}+{\mathcal{B}}_{z}\beta \mathrm{sin}\left(\beta z\right)\right]dz=0.$$

Appendix 2

$$\left\{{A}_{11}^{*},{A}_{22}^{*},{B}_{11}^{*},{B}_{22}^{*},{C}_{11}^{*},{C}_{22}^{*}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{E}_{f}}{1-{\nu }_{f}^{2}}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{E\left(z\right)}{1-\nu {\left(z\right)}^{2}}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{E}_{f}}{1-{\nu }_{f}^{2}}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\}dz,$$

$$\left\{{D}_{11}^{*},{D}_{22}^{*},{F}_{11}^{*},{F}_{22}^{*},{H}_{11}^{*},{H}_{22}^{*}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{E}_{f}}{1-{\nu }_{f}^{2}}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{E\left(z\right)}{1-\nu {\left(z\right)}^{2}}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{E}_{f}}{1-{\nu }_{f}^{2}}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz,$$

$$\left\{{A}_{12}^{*},{B}_{12}^{*},{C}_{12}^{*},{D}_{12}^{*},{F}_{12}^{*},{H}_{12}^{*}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{\nu }_{f}{E}_{f}}{1-{\nu }_{f}^{2}}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz +{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{\nu \left(z\right)E\left(z\right)}{1-\nu {\left(z\right)}^{2}}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{\nu }_{f}{E}_{f}}{1-{\nu }_{f}^{2}}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz,$$

$$\left\{{A}_{66}^{*},{B}_{66}^{*},{C}_{66}^{*},{D}_{66}^{*},{F}_{66}^{*},{H}_{66}^{*}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{E}_{f}}{2\left(1+{\nu }_{f}\right)}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{E(z)}{2\left(1+\nu (z)\right)}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{E}_{f}}{2\left(1+{\nu }_{f}\right)}\left\{1,z,\frac{4{z}^{3}}{3{h}^{2}},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz,$$

$$\left\{{A}_{44}^{*},{A}_{55}^{*},{D}_{44}^{*},{D}_{55}^{*},{F}_{44}^{*},{F}_{55}^{*}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{E}_{f}}{2\left(1+{\nu }_{f}\right)}\left\{\mathrm{1,1},\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{E(z)}{2\left(1+\nu (z)\right)}\left\{\mathrm{1,1},\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{E}_{f}}{2\left(1+{\nu }_{f}\right)}\left\{\mathrm{1,1},\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz,$$

$$\left\{{\mathcal{A}}_{11}^{**},{\mathcal{A}}_{22}^{**},{\mathcal{D}}_{11}^{**},{\mathcal{D}}_{22}^{**},,{\mathcal{F}}_{11}^{**},{\mathcal{F}}_{22}^{**}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{\mathrm{1,1},,\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{{l}^{2}E(z)}{1+\nu (z)}\left\{\mathrm{1,1},,\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{\mathrm{1,1},,\frac{4{z}^{2}}{{h}^{2}},\frac{4{z}^{2}}{{h}^{2}},\frac{16{z}^{4}}{{h}^{4}},\frac{16{z}^{4}}{{h}^{4}}\right\}dz,$$

$$\left\{{\mathcal{A}}_{44}^{**},{\mathcal{A}}_{55}^{**},{\mathcal{B}}_{44}^{**},{\mathcal{B}}_{55}^{**},{\mathcal{C}}_{44}^{**},{\mathcal{C}}_{55}^{**}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\}+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{{l}^{2}E(z)}{1+\nu (z)}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\}+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{\mathrm{1,1},z,z,\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{3}}{3{h}^{2}}\right\},$$

$$\left\{{\mathcal{D}}_{44}^{**},{\mathcal{D}}_{55}^{**},{\mathcal{F}}_{44}^{**},{\mathcal{F}}_{55}^{**},{\mathcal{H}}_{44}^{**},{\mathcal{H}}_{55}^{**}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}+{\int }_{-\frac{h}{2}}^\frac{h}{2}\frac{{l}^{2}E(z)}{1+\nu (z)}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}\frac{{l}^{2}{E}_{f}}{1+{\nu }_{f}}\left\{{z}^{2},{z}^{2},\frac{4{z}^{4}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}},\frac{16{z}^{6}}{9{h}^{4}}\right\}.$$

Im addition, the moments of inertia can be derived as:

$$\left\{{I}_{0},{I}_{1},{I}_{2},{I}_{3},{I}_{4},{I}_{6}\right\}={\int }_{-\frac{h}{2}-{h}_{f}}^{-\frac{h}{2}}{\rho }_{f}\left\{1,z,{z}^{2},\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_{-\frac{h}{2}}^\frac{h}{2}\rho (z)\left\{1,z,{z}^{2},\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz+{\int }_\frac{h}{2}^{\frac{h}{2}+{h}_{f}}{\rho }_{f}\left\{1,z,{z}^{2},\frac{4{z}^{3}}{3{h}^{2}},\frac{4{z}^{4}}{3{h}^{2}},\frac{16{z}^{6}}{9{h}^{4}}\right\}dz,$$

where ${E}_{f}, {\nu }_{f}$ and ${\rho }_{f}$ are, respectively, the Young’s modulus, Poisson’s ratio and mass density of the magnetostrictive facesheets. In addition, ${h}_{f}$ denotes the thickness of the magnetostrictive facesheets which are equal to ${h}_{f}=h/10$.