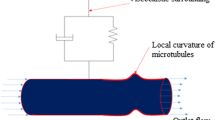
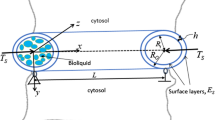
Abstract
The stability analysis of cantilevered curved microtubules in axons regarding various size elements and using the generalized differential quadrature method for solving equations is reported. The impacts of covering MAP Tau proteins along with cytoplasm are taken into account as the elastic medium. Curved cylindrical nanoshell considering thick wall is used to model the microtubules. The factor of length scale (l/R = 0.2) used in modified couple stress theory would result in more accuracy when it comes to comparison with experiments, while alternative theories presented in this paper provide less precise outcomes. Due to the reported precise results, at the lower value of the time-dependent viscoelastic factor (\({\tau }_{s})\) by rising the size-dependent factor, the frequency response of the cantilever microtubule increases and this relation between the size-dependent parameter and the structure’s natural frequency is changed from direct to indirect for the higher amount of the time-based viscoelastic factor that scientists should attend to this matter when it comes to the microtubule. Furthermore, physical neighboring situations in a cell will be prominent in microtubules’ dynamic stability responses, such as membrane and cell-matrix. Since microtubules are likely to be applied as biosensors, this feature could be employed to disclose virulent tumors.
















Similar content being viewed by others
References
Zhao X, Li D, Yang B, Ma C, Zhu Y, Chen H (2014) Feature selection based on improved ant colony optimization for online detection of foreign fiber in cotton. Appl Soft Comput 24:585–596
Wang M, Chen H (2020) Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl Soft Comput 88:105946
Zhao X, Zhang X, Cai Z, Tian X, Wang X, Huang Y et al (2019) Chaos enhanced grey wolf optimization wrapped ELM for diagnosis of paraquat-poisoned patients. Comput Biol Chem 78:481–490
Xu X, Chen H-L (2014) Adaptive computational chemotaxis based on field in bacterial foraging optimization. Soft Comput 18:797–807
Shen L, Chen H, Yu Z, Kang W, Zhang B, Li H et al (2016) Evolving support vector machines using fruit fly optimization for medical data classification. Knowl-Based Syst 96:61–75
Wang M, Chen H, Yang B, Zhao X, Hu L, Cai Z et al (2017) Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing 267:69–84
Xu Y, Chen H, Luo J, Zhang Q, Jiao S, Zhang X (2019) Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf Sci 492:181–203
Chen H, Zhang Q, Luo J, Xu Y, Zhang X (2020) An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl Soft Comput 86:105884
Gao W, Dimitrov D, Abdo H (2018) Tight independent set neighborhood union condition for fractional critical deleted graphs and ID deleted graphs. Discrete Continuous Dyn Syst S 12:711–721
Gao W, Guirao JLG, Basavanagoud B, Wu J (2018) Partial multi-dividing ontology learning algorithm. Inf Sci 467:35–58
Gao W, Wang W, Dimitrov D, Wang Y (2018) Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab J Chem 11:793–801
Gao W, Wu H, Siddiqui MK, Baig AQ (2018) Study of biological networks using graph theory. Saudi J Biol Sci 25:1212–1219
Gao W, Guirao JLG, Abdel-Aty M, Xi W (2019) An independent set degree condition for fractional critical deleted graphs. Discrete Continuous Dyn Syst S 12:877–886
Hawkins T, Mirigian M, Yasar MS, Ross JL (2010) Mechanics of microtubules. J Biomech 43:23–30
Brouhard GJ, Rice LM (2018) Microtubule dynamics: an interplay of biochemistry and mechanics. Nat Rev Mol Cell Biol 19:451–463
Beni YT, Zeverdejani MK, Mehralian F (2019) Using a new size dependent orthotropic elastic shell model for the investigation of free vibration of protein microtubules. Int J Acoust Vib 24:85–96
Bachmann S, Froese R, Cytrynbaum EN (2019) A buckling instability and its influence on microtubule orientation in plant cells. SIAM J Appl Math 79:2132–2149
Ntafam PN. Docteur de la communaute université grenoble alpES
Amos LA, Schlieper D (2005) Microtubules and maps. Adv Protein Chem 71:257–298
Long AF, Kuhn J, Dumont S (2019) The mammalian kinetochore–microtubule interface: robust mechanics and computation with many microtubules. Curr Opin Cell Biol 60:60–67
Tolić IM, Gerlich DW (2019) Spindle mechanics and chromosome segregation. Mol Biol Cell 30:735–736
Priya R, Kavitha L, Gopi D (2019) Dynamic instability in neuronal microtubules. Mater Today Proc. https://doi.org/10.1016/j.matpr.2019.07.312
Qiao W, Moayedi H, Foong LK (2020) Nature-inspired hybrid techniques of IWO, DA, ES, GA, and ICA, validated through a k-fold validation process predicting monthly natural gas consumption. Energy Buildings. https://doi.org/10.1016/j.enbuild.2020.110023
Weibiao Q, Bingfan L, Zhangyang K (2019) Differential scanning calorimetry and electrochemical tests for the analysis of delamination of 3PE coatings. Int J Electrochem Sci 14:7389–7400
Ghorbanpour Arani A, Abdollahian M, Ghorbanpour Arani A (2015) Modified Couple Stress Theory for Vibration of Embedded Bioliquid-Filled Microtubules under Walking a Motor Protein Including Surface Effects. J Solid Mech 7:458–476
Zhang J, Wang C (2016) Free vibration analysis of microtubules based on the molecular mechanics and continuum beam theory. Biomech Model Mechanobiol 15:1069–1078
Safeer M, Taj M, Abbas SS (2019) Effect of viscoelastic medium on wave propagation along protein microtubules. AIP Adv 9:045108
Xiang P, Zhang L, Liew K (2016) A mesh-free computational framework for predicting vibration behaviors of microtubules in an elastic medium. Compos Struct 149:41–53
Civalek Ö, Demir C (2016) A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl Math Comput 289:335–352
Beni YT, Zeverdejani MK (2015) Free vibration of microtubules as elastic shell model based on modified couple stress theory. J Mech Med Biol 15:1550037
Baninajjaryan A, Beni YT (2015) Theoretical study of the effect of shear deformable shell model, elastic foundation and size dependency on the vibration of protein microtubule. J Theor Biol 382:111–121
Arani AG, Abdollahian M, Jalaei M (2015) Vibration of bioliquid-filled microtubules embedded in cytoplasm including surface effects using modified couple stress theory. J Theor Biol 367:29–38
Farajpour A, Rastgoo A (2017) Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results Phys 7:1367–1375
Kamali M, Shamsi M, Saidi A (2018) Surface effect on buckling of microtubules in living cells using first-order shear deformation shell theory and standard linear solid model. Mech Res Commun 92:111–117
Beni YT, Zeverdejani MK, Mehralian F (2017) Buckling analysis of orthotropic protein microtubules under axial and radial compression based on couple stress theory. Math Biosci 292:18–29
Sedighi HM, Sheikhanzadeh A (2017) Static and dynamic pull-in instability of nano-beams resting on elastic foundation based on the nonlocal elasticity theory. Chin J Mech Eng 30:385–397
Salamat D, Sedighi HM (2017) The effect of small scale on the vibrational behavior of single-walled carbon nanotubes with a moving nanoparticle. J Appl Comput Mech 3:208–217
Ghodrati B, Yaghootian A, Ghanbar Zadeh A, Mohammad-Sedighi H (2018) Lamb wave extraction of dispersion curves in micro/nano-plates using couple stress theories. Waves Random Complex media 28:15–34
Jamali M, Shojaee T, Mohammadi B, Kolahchi R (2019) Cut out effect on nonlinear post-buckling behavior of FG-CNTRC micro plate subjected to magnetic field via FSDT. Adv Nano Res 7:405–417
Sedighi HM (2020) Divergence and flutter instability of magneto-thermo-elastic C-BN hetero-nanotubes conveying fluid. Acta Mech Sin. https://doi.org/10.1007/s10409-019-00924-4
Sedighi HM, Yaghootian A (2016) Dynamic instability of vibrating carbon nanotubes near small layers of graphite sheets based on nonlocal continuum elasticity. J Appl Mech Tech Phys 57:90–100
Soheilypour M, Peyro M, Peter SJ, Mofrad MR (2015) Buckling behavior of individual and bundled microtubules. Biophys J 108:1718–1726
Batou B, Nebab M, Bennai R, Atmane HA, Tounsi A, Bouremana M (2019) Wave dispersion properties in imperfect sigmoid plates using various HSDTs. Steel Compos Struct 33:699
Salah F, Boucham B, Bourada F, Benzair A, Bousahla AA, Tounsi A (2019) Investigation of thermal buckling properties of ceramic-metal FGM sandwich plates using 2D integral plate model. Steel Compos Struct 33:805
Sahmani S, Fattahi A, Ahmed N (2020) Develop a refined truncated cubic lattice structure for nonlinear large-amplitude vibrations of micro/nano-beams made of nanoporous materials. Eng Comput 36:359–375
Hajmohammad MH, Nouri AH, Zarei MS, Kolahchi R (2019) A new numerical approach and visco-refined zigzag theory for blast analysis of auxetic honeycomb plates integrated by multiphase nanocomposite facesheets in hygrothermal environment. Eng Comput 35:1141–1157
Ayat H, Kellouche Y, Ghrici M, Boukhatem B (2018) Compressive strength prediction of limestone filler concrete using artificial neural networks. Adv Comput Des 3:289–302
Behera S, Kumari P (2018) Free vibration of Levy-type rectangular laminated plates using efficient zig-zag theory. Adv Comput Design 3:213–232
Narwariya M, Choudhury A, Sharma AK (2018) Harmonic analysis of moderately thick symmetric cross-ply laminated composite plate using FEM. Adv Comput Design 3:113–132
Sedighi HM, Reza A, Zare J (2011) Study on the frequency–amplitude relation of beam vibration. Int J Phys Sci 6:8051–8056
Ghorbanpour Arani A, Rousta Navi B, Mohammadimehr M, Niknejad S, Ghorbanpour Arani A, Hosseinpour A (2019) Pull-in instability of MSGT piezoelectric polymeric FG-SWCNTs reinforced nanocomposite considering surface stress effect. J Solid Mech 11:759–777
Ghorbanpour Arani A, Emdadi M, Ashrafi H, Mohammadimehr M, Niknejad S, Ghorbanpour Arani A et al (2019) Analysis of viscoelastic functionally graded sandwich plates with CNT reinforced composite face sheets on viscoelastic foundation. J Solid Mech 11:690–706
Aria AI, Biglari H (2018) Computational vibration and buckling analysis of microtubule bundles based on nonlocal strain gradient theory. Appl Math Comput 321:313–332
Farajpour A, Rastgoo A, Mohammadi M (2017) Vibration, buckling and smart control of microtubules using piezoelectric nanoshells under electric voltage in thermal environment. Phys B 509:100–114
Akgöz B, Civalek Ö (2011) Application of strain gradient elasticity theory for buckling analysis of protein microtubules. Curr Appl Phys 11:1133–1138
Civalek Ö (2017) Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Compos B Eng 111:45–59
Bahaadini R, Hosseini M, Amiri M (2020) Dynamic stability of viscoelastic nanotubes conveying pulsating magnetic nanoflow under magnetic field. Eng Comput. https://doi.org/10.1007/s00366-020-00980-6
Demir Ç, Civalek Ö (2017) On the analysis of microbeams. Int J Eng Sci 121:14–33
Ebrahimi F, Hosseini SH (2020) Nonlinear dynamics and stability of viscoelastic nanoplates considering residual surface stress and surface elasticity effects: a parametric excitation analysis. Eng Comput. https://doi.org/10.1007/s00366-019-00906-x
Sahmani S, Fattahi A, Ahmed N (2019) Analytical mathematical solution for vibrational response of postbuckled laminated FG-GPLRC nonlocal strain gradient micro-/nanobeams. Eng Comput 35:1173–1189
Sofiyev AH, Avcar M (2010) The stability of cylindrical shells containing an FGM layer subjected to axial load on the Pasternak foundation. Engineering 2:228
Sofiyev A, Alizada A, Akin Ö, Valiyev A, Avcar M, Adiguzel S (2012) On the stability of FGM shells subjected to combined loads with different edge conditions and resting on elastic foundations. Acta Mech 223:189–204
Wu Q, Chen H, Gao W (2019) Nonlocal strain gradient forced vibrations of FG-GPLRC nanocomposite microbeams. Eng Comput. https://doi.org/10.1007/s00366-019-00794-1
Yang X, Sahmani S, Safaei B (2020) Postbuckling analysis of hydrostatic pressurized FGM microsized shells including strain gradient and stress-driven nonlocal effects. Eng Comput. https://doi.org/10.1007/s00366-019-00901-2
Moayedi H, Darabi R, Ghabussi A, Habibi M, Foong LK (2020) Weld orientation effects on the formability of tailor welded thin steel sheets. Thin-Walled Struct 149:106669
Ghazanfari A, Soleimani SS, Keshavarzzadeh M, Habibi M, Assempuor A, Hashemi R (2019) Prediction of FLD for sheet metal by considering through-thickness shear stresses. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1662310
Alipour M, Torabi MA, Sareban M, Lashini H, Sadeghi E, Fazaeli A, Habibi M, Hashemi R (2019) Finite element and experimental method for analyzing the effects of martensite morphologies on the formability of DP steels. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1633343
Hosseini S, Habibi M, Assempour A (2018) Experimental and numerical determination of forming limit diagram of steel-copper two-layer sheet considering the interface between the layers. Modares Mech Eng 18:174–181
Habibi M, Hashemi R, Ghazanfari A, Naghdabadi R, Assempour A (2018) Forming limit diagrams by including the M–K model in finite element simulation considering the effect of bending. Proc Inst Mech Eng L J Mater Design Appl 232:625–636
Habibi M, Payganeh G (2018) Experimental and finite element investigation of titanium tubes hot gas forming and production of square cross-section specimens. Aerosp Mech J 14(2(52)):89–99
Habibi M, Hashemi R, Tafti MF, Assempour A (2018) Experimental investigation of mechanical properties, formability and forming limit diagrams for tailor-welded blanks produced by friction stir welding. J Manuf Process 31:310–323
Habibi M, Ghazanfari A, Assempour A, Naghdabadi R, Hashemi R (2017) Determination of forming limit diagram using two modified finite element models. Mech Eng 48:141–144
Ghazanfari A, Assempour A, Habibi M, Hashemi R (2016) Investigation on the effective range of the through thickness shear stress on forming limit diagram using a modified Marciniak–Kuczynski model. Modares Mech Eng 16:137–143
Habibi M, Hashemi R, Sadeghi E, Fazaeli A, Ghazanfari A, Lashini H (2016) Enhancing the mechanical properties and formability of low carbon steel with dual-phase microstructures. J Mater Eng Perform 25:382–389
Fazaeli A, Habibi M, Ekrami A (2016) Experimental and Finite Element Comparison of Mechanical Properties and Formability of Dual Phase Steel and Ferrite-Pearlite Steel With the Same Chemical Composition. Metall Eng 19(2):84–93
Ebrahimi F, Mohammadi K, Barouti MM, Habibi M (2019) Wave propagation analysis of a spinning porous graphene nanoplatelet-reinforced nanoshell. Waves Random Complex Media 1–27
Hashemi HR, Alizadeh AA, Oyarhossein MA, Shavalipour A, Makkiabadi M, Habibi M (2019) Influence of imperfection on amplitude and resonance frequency of a reinforcement compositionally graded nanostructure. Waves Random Complex Media. https://doi.org/10.1080/17455030.2019.1662968
Modaresahmadi S, Hosseinpour A, Williams WB (2019) Fatigue life prediction of a coaxial multi-stage magnetic gear. In: 2019 IEEE Texas power and energy conference (TPEC), pp 1-6
Ghadiri M, Safarpour H (2016) Free vibration analysis of embedded magneto-electro-thermo-elastic cylindrical nanoshell based on the modified couple stress theory. Appl Phys A 122:833
Safarpour M, Ghabussi A, Ebrahimi F, Habibi M, Safarpour H (2020) Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin Walled Struct 150:106683
Safarpour M, Ebrahimi F, Habibi M, Safarpour H (2020) On the nonlinear dynamics of a multi-scale hybrid nanocomposite disk. Eng Comput. https://doi.org/10.1007/s00366-020-00949-5
Moayedi H, Habibi M, Safarpour H, Safarpour M, Foong L Buckling and frequency responses of a graphene nanoplatelet reinforced composite microdisk. Int J Appl Mech
Zhang X, Shamsodin M, Wang H, Noormohammadi Arani O, Khan AM, Habibi M, Al-Furjan MSH (2020) Dynamic information of the time-dependent tobullian biomolecular structure using a high-accuracy size-dependent theory. J Biomol Struct Dyn. https://doi.org/10.1080/07391102.2020.1760939
Safarpour H, Barooti M, Ghadiri M (2019) Influence of rotation on vibration behavior of a functionally graded moderately thick cylindrical nanoshell considering initial hoop tension. J Solid Mech 11:254–271
Ebrahimi F, Safarpour H (2018) Vibration analysis of inhomogeneous nonlocal beams via a modified couple stress theory incorporating surface effects. Wind Struct 27:431–438
Mohammadi K, Barouti MM, Safarpour H, Ghadiri M (2019) Effect of distributed axial loading on dynamic stability and buckling analysis of a viscoelastic DWCNT conveying viscous fluid flow. J Braz Soc Mech Sci Eng 41:93
SafarPour H, Hosseini M, Ghadiri M (2017) Influence of three-parameter viscoelastic medium on vibration behavior of a cylindrical nonhomogeneous microshell in thermal environment: an exact solution. J Therm Stresses 40:1353–1367
Safarpour H, Mohammadi K, Ghadiri M, Barooti MM (2018) Effect of porosity on flexural vibration of CNT-reinforced cylindrical shells in thermal environment using GDQM. Int J Struct Stab Dyn 18:1850123
Safarpour H, Mohammadi K, Ghadiri M (2017) Temperature-dependent vibration analysis of a FG viscoelastic cylindrical microshell under various thermal distribution via modified length scale parameter: a numerical solution. J Mech Behav Mater 26:9–24
SafarPour H, Ghanbari B, Ghadiri M (2019) Buckling and free vibration analysis of high speed rotating carbon nanotube reinforced cylindrical piezoelectric shell. Appl Math Model 65:428–442
Shojaeefard M, Mahinzare M, Safarpour H, Googarchin HS, Ghadiri M (2018) Free vibration of an ultra-fast-rotating-induced cylindrical nano-shell resting on a Winkler foundation under thermo-electro-magneto-elastic condition. Appl Math Model 61:255–279
Ghadiri M, SafarPour H (2017) Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J Therm Stresses 40:55–71
Ghadiri M, Shafiei N, Safarpour H (2017) Influence of surface effects on vibration behavior of a rotary functionally graded nanobeam based on Eringen’s nonlocal elasticity. Microsyst Technol 23:1045–1065
SafarPour H, Ghadiri M (2017) Critical rotational speed, critical velocity of fluid flow and free vibration analysis of a spinning SWCNT conveying viscous fluid. Microfluid Nanofluid 21:22
Barooti MM, Safarpour H, Ghadiri M (2017) Critical speed and free vibration analysis of spinning 3D single-walled carbon nanotubes resting on elastic foundations. Eur Phys J Plus 132:6
SafarPour H, Mohammadi K, Ghadiri M, Rajabpour A (2017) Influence of various temperature distributions on critical speed and vibrational characteristics of rotating cylindrical microshells with modified lengthscale parameter. Eur Phys J Plus 132:281
Shokrgozar A, Ghabussi A, Ebrahimi F, Habibi M, Safarpour H (2020) Viscoelastic dynamics and static responses of a graphene nanoplatelets-reinforced composite cylindrical microshell. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2020.1719509
Ebrahimi F, Supeni EEB, Habibi M, Safarpour H (2020) Frequency characteristics of a GPL-reinforced composite microdisk coupled with a piezoelectric layer. Eur Phys J Plus 135:144
Ebrahimi F, Hashemabadi D, Habibi M, Safarpour H (2020) Thermal buckling and forced vibration characteristics of a porous GNP reinforced nanocomposite cylindrical shell. Microsyst Technol 26(2):461–473. https://doi.org/10.1007/s00542-019-04542-9
Moayedi H, Aliakbarlou H, Jebeli M, Noormohammadiarani O, Habibi M, Safarpour H, Foong LK (2020) Thermal buckling responses of a graphene reinforced composite micropanel structure. Int J Appl Mech. https://doi.org/10.1142/S1758825120500106
Shokrgozar A, Safarpour H, Habibi M (2020) Influence of system parameters on buckling and frequency analysis of a spinning cantilever cylindrical 3D shell coupled with piezoelectric actuator. Proc Inst Mech Eng C J Mech Eng Sc 234:512–529
Ghabussi A, Ashrafi N, Shavalipour A, Hosseinpour A, Habibi M, Moayedi H, Babaei B, Safarpour H (2019) Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1705166
Habibi M, Mohammadi A, Safarpour H, Ghadiri M (2019) Effect of porosity on buckling and vibrational characteristics of the imperfect GPLRC composite nanoshell. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.17014900
Habibi M, Mohammadi A, Safarpour H, Shavalipour A, Ghadiri M (2019) Wave propagation analysis of the laminated cylindrical nanoshell coupled with a piezoelectric actuator. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1697932
Habibi M, Taghdir A, Safarpour H (2019) Stability analysis of an electrically cylindrical nanoshell reinforced with graphene nanoplatelets. Compos B Eng 175:107125
Mohammadgholiha M, Shokrgozar A, Habibi M, Safarpour H (2019) Buckling and frequency analysis of the nonlocal strain–stress gradient shell reinforced with graphene nanoplatelets. J Vib Control 25:2627–2640
Ebrahimi F, Habibi M, Safarpour H (2019) On modeling of wave propagation in a thermally affected GNP-reinforced imperfect nanocomposite shell. Eng Comput 35:1375–1389
Safarpour H, Hajilak ZE, Habibi M (2019) A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures restring on elastic foundation. Int J Mech Mater Des 15:569–583
Esmailpoor Hajilak Z, Pourghader J, Hashemabadi D, Sharifi Bagh F, Habibi M, Safarpour H (2019) Multilayer GPLRC composite cylindrical nanoshell using modified strain gradient theory. Mech Based Design Struct Mach 47:521–545
Ebrahimi F, Hajilak ZE, Habibi M, Safarpour H (2019) Buckling and vibration characteristics of a carbon nanotube-reinforced spinning cantilever cylindrical 3D shell conveying viscous fluid flow and carrying spring-mass systems under various temperature distributions. Proc Inst Mech Eng C J Mech Eng Sci 233:4590–4605
Mohammadi A, Lashini H, Habibi M, Safarpour H (2019) Influence of viscoelastic foundation on dynamic behaviour of the double walled cylindrical inhomogeneous micro shell using MCST and with the aid of GDQM. J Solid Mech 11:440–453
Habibi M, Hashemabadi D, Safarpour H (2019) Vibration analysis of a high-speed rotating GPLRC nanostructure coupled with a piezoelectric actuator. Eur Phys J Plus 134:307
Pourjabari A, Hajilak ZE, Mohammadi A, Habibi M, Safarpour H (2019) Effect of porosity on free and forced vibration characteristics of the GPL reinforcement composite nanostructures. Comput Math Appl 77:2608–2626
Habibi M, Mohammadgholiha M, Safarpour H (2019) Wave propagation characteristics of the electrically GNP-reinforced nanocomposite cylindrical shell. J Braz Soc Mech Sci Eng 41:221
Safarpour H, Pourghader J, Habibi M (2019) Influence of spring-mass systems on frequency behavior and critical voltage of a high-speed rotating cantilever cylindrical three-dimensional shell coupled with piezoelectric actuator. J Vib Control 25:1543–1557
Safarpour H, Ghanizadeh SA, Habibi M (2018) Wave propagation characteristics of a cylindrical laminated composite nanoshell in thermal environment based on the nonlocal strain gradient theory. Eur Phys J Plus 133:532
Moayedi H, Ebrahimi F, Habibi M, Safarpour H, Foong LK (2020) Application of nonlocal strain–stress gradient theory and gdqem for thermo-vibration responses of a laminated composite nanoshell. Eng Comput. https://doi.org/10.1007/s00366-020-01002-1
Cheshmeh E, Karbon M, Eyvazian A, Jung DW, Habibi M, Safarpour M (2020) Buckling and vibration analysis of FG-CNTRC plate subjected to thermo-mechanical load based on higher order shear deformation theory. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2020.1744005
Oyarhossein MA, A. a. Alizadeh, M. Habibi, M. Makkiabadi, M. Daman, H. Safarpour, et al (2020) Dynamic response of the nonlocal strain-stress gradient in laminated polymer composites microtubes. Sci Rep 10:5616
Najaafi N, Jamali M, Habibi M, Sadeghi S, Jung DW, Nabipour N (2020) Dynamic instability responses of the substructure living biological cells in the cytoplasm environment using stress-strain size-dependent theory. J Biomol Struct Dyn. https://doi.org/10.1080/07391102.2020.1751297
Abdelmalek Z, Karbon M, Eyvazian A, Foroughi A, Safarpour H, Tlili I (2020) On the dynamics of a curved Microtubule-associated proteins by considering viscoelastic properties of the living biological cells. J Biomol Struct Dyn. https://doi.org/10.1080/07391102.2020.1747549
Marzbanrad J, Hoseinpour A (2017) Structural optimization of MacPherson control arm under fatigue loading. Tehnički vjesnik 24:917–924
Safarpour M, Rahimi AR, Alibeigloo A (2019) Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1646137
Shahgholian-Ghahfarokhi D, Safarpour M, Rahimi A (2019) Torsional buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (GPLs). Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2019.1666723
Bisheh H, Alibeigloo A, Safarpour M, Rahimi A (2019) Three-dimensional static and free vibrational analysis of graphene reinforced composite circular/annular plate using differential quadrature method. Int J Appl Mech 11:1950073
Safarpour M, Rahimi A, Alibeigloo A, Bisheh H, Forooghi A (2019) Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech Based Design Struct Mach 1–31
A Rahimi, A Alibeigloo, M Safarpour (2020) Three-dimensional static and free vibration analysis of graphene platelet–reinforced porous composite cylindrical shell. J Vib Control. doi:10.1177/1077546320902340
Wang Y, Zeng R, Safarpour M (2020) Vibration analysis of FG-GPLRC annular plate in a thermal environment. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2020.1719508
Shahgholian D, Safarpour M, Rahimi AR, Alibeigloo A (2020) Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh–Ritz method. Acta Mech. https://doi.org/10.1007/s00707-020-02616-8
Shariati A, Mohammad-Sedighi H, Żur KK, Habibi M, Safa M (2020) Stability and dynamics of viscoelastic moving Rayleigh beams with an asymmetrical distribution of material parameters. Symmetry 12:586
Shariati A, Mohammad-Sedighi H, Żur KK, Habibi M, Safa M (2020) On the vibrations and stability of moving viscoelastic axially functionally graded nanobeams. Materials 13:1707
Jermsittiparsert K, Ghabussi A, Forooghi A, Shavalipour A, Habibi M, won Jung D, Safa M (2020) Critical voltage, thermal buckling and frequency characteristics of a thermally affected GPL reinforced composite microdisk covered with piezoelectric actuator. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2020.1748052
Ghabussi A, Marnani JA, Rohanimanesh MS (2020) Improving seismic performance of portal frame structures with steel curved dampers. Structures 24:27–40. https://doi.org/10.1016/j.istruc.2019.12.025
Bellman R, Casti J (1971) Differential quadrature and long-term integration. J Math Anal Appl 34:235–238
Bellman R, Kashef B, Casti J (1972) Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations. J Comput Phys 10:40–52
Eyvazian A, Hamouda AM, Tarlochan F, Mohsenizadeh S, Dastjerdi AA (2019) Damping and vibration response of viscoelastic smart sandwich plate reinforced with non-uniform Graphene platelet with magnetorheological fluid core. Steel Compos Struct 33:891
Motezaker M, Eyvazian A (2020) Post-buckling analysis of Mindlin Cut out-plate reinforced by FG-CNTs. Steel Compos Struct 34:289
Shu C (2012) Differential quadrature and its application in engineering. Springer, Berlin
Shu C, Richards BE (1992) Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. Int J Numer Methods Fluids 15:791–798
Derazkola HA, Eyvazian A, Simchi A (2020) Modeling and experimental validation of material flow during FSW of polycarbonate. Mater Today Commun 22:100796
Eyvazian A, Hamouda A, Tarlochan F, Derazkola HA, Khodabakhshi F (2020) Simulation and experimental study of underwater dissimilar friction-stir welding between aluminium and steel. J Mater Res Technol. https://doi.org/10.1016/j.jmrt.2020.02.003
Gasser L (1987) Free vibrations of thin cylindrical shells containing liquid. MS Thesis
Gonçalves PB, Ramos NR (1997) Numerical method for vibration analysis of cylindrical shells. J Eng Mech 123:544–550
Dym CL (1973) Some new results for the vibrations of circular cylinders. J Sound Vib 29:189–205
Shen H-S, Xiang Y (2012) Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput Methods Appl Mech Eng 213:196–205
Kurachi M, Hoshi M, Tashiro H (1995) Buckling of a single microtubule by optical trapping forces: direct measurement of microtubule rigidity. Cell Motil Cytoskelet 30:221–228
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Shariati, A., Habibi, M., Tounsi, A. et al. Application of exact continuum size-dependent theory for stability and frequency analysis of a curved cantilevered microtubule by considering viscoelastic properties. Engineering with Computers 37, 3629–3648 (2021). https://doi.org/10.1007/s00366-020-01024-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01024-9