Skip to main content
SpringerLink
Log in

Optimal stochastic restricted logistic estimator

  • Regular Article
  • Published:
Statistical Papers Aims and scope Submit manuscript

Abstract

It is well known that the use of prior information in the logistic regression improves the estimates of regression coefficients when multicollinearity presents. This prior information may be in the form of exact or stochastic linear restrictions. In this article, in the presence of stochastic linear restrictions, we propose a new efficient estimator, named Stochastic restricted optimal logistic estimator for the parameters in the logistic regression models when the multicollinearity presents. Further, conditions for the superiority of the new optimal estimator over some existing estimators are derived with respect to the mean square error matrix sense. Moreover, a Monte Carlo simulation study and a real data example are provided to illustrate the performance of the proposed optimal estimator in the scalar mean square error sense.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  • Aguilera AM, Escabias M, Valderrama MJ (2006) Using principal components for estimating logistic regression with high-dimensional multicollinear data. Comput. Stat. Data Anal. 50:1905–1924

    Article  MathSciNet  Google Scholar 

  • Asar Y, Arashi M, Wu J (2017a) Restricted ridge estimator in the logistic regression model. Commun Stat Simul Comput 46(8):6538–6544

    Article  MathSciNet  Google Scholar 

  • Asar Y, Erişoǧlu M, Arashi M (2017b) Developing a restricted two-parameter Liu-type estimator: a comparison of restricted estimators in the binary logistic regression model. Commun Stat Theory Method 46(14):6864–6873

    Article  MathSciNet  Google Scholar 

  • Asar Y, Genç A (2016) New shrinkage parameters for the Liu-type logistic estimators. Commun Stat Simul Comput 45(3):1094–1103

    Article  MathSciNet  Google Scholar 

  • Cox D (1958) The regression analysis of binary sequences (with discussion). J R Stat Soc B 20(2):215–242

    MATH  Google Scholar 

  • Duffy DE, Santner TJ (1989) On the small sample prosperities of norm-restricted maximum likelihood estimators for logistic regression models. Commun Stat Theory Methods 18:959–980

    Article  Google Scholar 

  • Inan D, Erdogan BE (2013) Liu-type logistic estimator. Commun Stat Simul Comput 42:1578–1586

    Article  MathSciNet  Google Scholar 

  • Kibria BMG (2003) Performance of some new ridge regression estimators. Commun Stat Theory Methods 32:419–435

    MathSciNet  MATH  Google Scholar 

  • Mansson G, Kibria BMG, Shukur G (2012) On Liu estimators for the logit regression model. The Royal Institute of Techonology, Centre of Excellence for Science and Innovation Studies (CESIS), Sweden, Paper No. 259

  • Mansson K, Shukur G (2011) On ridge parameters in logistic regression. Commun Stat Theory Methods 40:3366–3381

    Article  MathSciNet  Google Scholar 

  • McDonald GC, Galarneau DI (1975) A Monte Carlo evaluation of some ridge type estimators. J Am Stat Assoc 70:407–416

    Article  Google Scholar 

  • Nagarajah V, Wijekoon P (2015) Stochastic restricted maximum likelihood estimator in logistic regression model. Open J Stat 5:837–851. https://doi.org/10.4236/ojs.2015.57082

    Article  Google Scholar 

  • Newhouse JP, Oman SD (1971) An evaluation of ridge estimators. RAND Corporation, Santa Monica

    Google Scholar 

  • Nja ME, Ogoke UP, Nduka EC (2013) A new logistic ridge regression estimator using exponentiated response function. J Stat Econ Methods 2(4):161–171

    Google Scholar 

  • Özkale MR (2015) Predictive performance of linear regression models. Stati Pap 56(2):531–67

    Article  MathSciNet  Google Scholar 

  • Rao CR, Toutenburg H, Shalabh HC (2008) Linear models and generalizations. Springer, Berlin

    MATH  Google Scholar 

  • Rao CR, Toutenburg H (1995) Linear models : least squares and alternatives, 2nd edn. Springer, New York

    Book  Google Scholar 

  • Schaefer RL, Roi LD, Wolfe RA (1984) A ridge logistic estimator. Commun Stat Theory Methods 13:99–113

    Article  Google Scholar 

  • Şiray GU, Toker S, Kaçiranlar S (2015) On the restricted Liu estimator in logistic regression model. Commun Stat Simul Comput 44:217–232

    Article  MathSciNet  Google Scholar 

  • Trenkler G, Toutenburg H (1990) Mean square error matrix comparisons between biased estimators? An overview of recent results. Stat Pap 31:165–179. https://doi.org/10.1007/BF02924687

    Article  MATH  Google Scholar 

  • van Howelingen HC, Sauerbrei W (2013) Cross-validation, shrinkage and variable selection in linear regression revisited. Open J Stat 03(02):79–102

    Article  Google Scholar 

  • Varathan N, Wijekoon P (2016a) On the restricted almost unbiased ridge estimator in logistic regression. Open J Stat 6:1076–1084. https://doi.org/10.4236/ojs.2016.66087

    Article  Google Scholar 

  • Varathan N, Wijekoon P (2016b) Ridge estimator in logistic regression under stochastic linear restriction. Br J Math Comput Sci 15(3):1. https://doi.org/10.9734/BJMCS/2016/24585

    Article  MATH  Google Scholar 

  • Varathan N, Wijekoon P (2016c) Logistic Liu estimator under stochastic linear restrictions. Stat Pap. https://doi.org/10.1007/s00362-016-0856-6

  • Varathan N, Wijekoon P (2017) A stochastic restricted almost unbiased ridge estimator in logistic regression. Proceedings of the iPURSE, University of Peradeniya, p 36. Accessed 24 Nov 2017

  • Varathan N, Wijekoon P (2018a) Optimal generalized logistic estimator. Commun Stat Theory Methods 47(2):463–474

    Article  MathSciNet  Google Scholar 

  • Varathan N, Wijekoon P (2018b) Liu-type logistic estimator under stochastic linear restrictions. Ceylon J Sci 47(1):21–34. https://doi.org/10.4038/cjs.v47i1.7483

    Article  MATH  Google Scholar 

  • Varathan N, Wijekoon P (2018c) An improved stochastic restricted almost unbiased Liu-estimator in logistic regression. J Mod Appl Stat Methods, Accepted

  • Wu J (2016) Modified restricted Liu estimator in logistic regression model. Comput Stat 31(4):1557–1567

    Article  MathSciNet  Google Scholar 

  • Wu J, Asar Y (2016) On almost unbiased ridge logistic estimator for the logistic regression model. Hacet J Math Stat 45(3):989–998. https://doi.org/10.15672/HJMS.20156911030

    Article  MathSciNet  MATH  Google Scholar 

  • Xinfeng C (2015) On the almost unbiased ridge and Liu estimator in the logistic regression model. In: International conference on social science, education management and sports education. Atlantis Press, Paris, pp 1663–1665

Download references

Author information

Authors and Affiliations

  1. Postgraduate Institute of Science, University of Peradeniya, Peradeniya, Sri Lanka

    Nagarajah Varathan

  2. Department of Mathematics and Statistics, University of Jaffna, Jaffna, Sri Lanka

    Nagarajah Varathan

  3. Department of Statistics and Computer Science, University of Peradeniya, Peradeniya, Sri Lanka

    Pushpakanthie Wijekoon

Authors
  1. Nagarajah Varathan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pushpakanthie Wijekoon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nagarajah Varathan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (xlsx 11 KB)

Appendices

Appendix A

See Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14.

Table 1 The optimal values of k, d for different \(\rho \) values when \(p=2\) and \(n = 20\)
Full size table
Table 2 The optimal values of k, d for different \(\rho \) values when \(p=2\) and \(n = 50\)
Full size table
Table 3 The optimal values of k, d for different \(\rho \) values when \(p=2\) and \(n = 100\)
Full size table
Table 4 The optimal values of k, d for different \(\rho \) values when \(p=4\) and \(n = 20\)
Full size table
Table 5 The optimal values of k, d for different \(\rho \) values when \(p=4\) and \(n = 50\)
Full size table
Table 6 The optimal values of k, d for different \(\rho \) values when \(p=4\) and \(n = 100\)
Full size table
Table 7 The estimated SMSE values for different \(\rho \) values when \(p=2\) and \(n = 20\)
Full size table
Table 8 The estimated SMSE values for different \(\rho \) values when \(p=2\) and \(n = 50\)
Full size table
Table 9 The estimated SMSE values for different \(\rho \) values when \(p=2\) and \(n = 100\)
Full size table
Table 10 The estimated SMSE values for different \(\rho \) values when \(p=4\) and \(n = 20\)
Full size table
Table 11 The estimated SMSE values for different \(\rho \) values when \(p=4\) and \(n = 50\)
Full size table
Table 12 The estimated SMSE values for different \(\rho \) values when \(p=4\) and \(n = 100\)
Full size table
Table 13 The optimal values of k, d for real data example
Full size table
Table 14 The SMSE values for real data example
Full size table

Appendix B

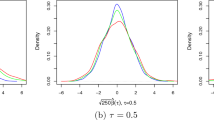
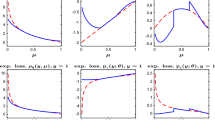
See Figs. 1, 2, 3, 4, 5 and 6.

Fig. 1
figure 1

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=2\), \(\hbox {n}=20\)

Full size image
Fig. 2
figure 2

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=2\), \(\hbox {n}=50\)

Full size image
Fig. 3
figure 3

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=2\), \(\hbox {n}=100\)

Full size image
Fig. 4
figure 4

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=4\), \(\hbox {n}=20\)

Full size image
Fig. 5
figure 5

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=4\), \(\hbox {n}=50\)

Full size image
Fig. 6
figure 6

Estimated SMSE values for SRMLE, SRRMLE, SRLMLE, SRAULLE, SRAURLE, SRLTLE, OGLE, and SROLE for \(\hbox {p}=4\), \(\hbox {n}=100\)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Varathan, N., Wijekoon, P. Optimal stochastic restricted logistic estimator. Stat Papers 62, 985–1002 (2021). https://doi.org/10.1007/s00362-019-01121-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00362-019-01121-y

Keywords

Search

Navigation