Abstract
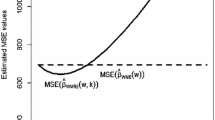
In this paper, a new estimator is proposed by combining basically the ordinary ridge regression estimator and the principal component regression estimator for a regression model which has multicollinearity and which satisfies some a priori stochastic linear restrictions. The performance of the proposed \(r{-}k\) class estimator in this mixed regression model is compared with those of the mixed regression estimator, ridge regression estimator and the stochastic restricted ridge regression estimator in terms of the mean squared error matrix criterion. Tests for verifying the conditions of dominance of the proposed estimator over the others are also proposed. Furthermore, a Monte Carlo study and a numerical illustration are carried out to empirically study the performance of the estimators by the mean squared error values, and then to perform tests to verify if the conditions for superiority of the proposed estimator over the others hold.


Similar content being viewed by others
Notes
Since the mean squared error matrix is the only criterion used in this paper for the purpose of comparison between two estimators, we use the abbreviation MSE to represent the mean squared error matrix all throughout this paper.
For brevity of space, the EMSE values are presented for one value of \(\phi \) \(viz\), \(\phi =0.5\), only and the process is AR(1) for both \(u_i\) and \(v_i\). The conclusions are same for the two other values of \(\phi \) i.e., \(\phi =0.2\) and \(0.8\), and for MA(1) process as well.
References
Baksalary JK, Trenkler G (1991) Nonnegative and positive definiteness of matrices modified by two matrices of rank one. Linear Algebra Appl 151:169–184
Baye MR, Parker DF (1984) Combining ridge and principal components regression:a money demand illustration. Commun Stat Theory Methods 13(2):197–205
Bayhan GM, Bayhan M (1998) Forecasting using autocorrelated errors and multicollinear predictor variables. Comput Ind Eng 34:413–421
Firinguetti L (1989) A simulation study of ridge regression estimators with autocorrelated errors. Commun Stat Simul Comput 18(2):673–702
Gujarati DN (2002) Basic econometrics, 4th edn. Tata McGraw-Hill, New York
Hoerl AE, Kennard RW (1970) Ridge regression:biased estimation for nonorthogonal problems. Technometrics 12:55–67
Johnson NL, Kotz S (1970) Distributions in statistics: Continuous Univariate Distributions - 2. Wiley, New York
Judge GG, Griffiths WE, Hill RC, Lütkepohl H, Lee TC (1985) The theory and practice of econometrics. John Wiley and Sons, New York
Kaçıranlar S, Sakallioğlu S (2001) Combining the Liu estimator and the principal component regression estimator. Commun Stat Theory Methods 30(12):2699–2705
Liu K (1993) A new class of biased estimate in linear regression. Comm Stat Theory Methods 22:393–402
Massy WF (1965) Principal components regression in exploratory statistical research. J Am Stat Assoc 60:234–266
Newhouse JP, Oman SD (1971) An evaluation of ridge estimators. Rand corporation, Santa Monica, pp 1–29
Özkale MR, Kaçiranlar S (2007) The restricted and unrestricted two parameter estimators. Commun Stat Theory Methods 36(15):2707–2725
Özkale MR, Kaçiranlar S (2008) Comparisons of the r-k class estimator to the ordinary least squares estimator under the Pitman’s closeness criterion. Stat Papers 49:503–512
Özkale MR (2009) A stochastic restricted ridge regression estimator. J Multivar Anal 100:1700–1706
Özkale MR (2012) Combining the unrestricted estimators into a single estimator and a simulation study on the unrestricted estimators. J Stat Comput Simul 62(4):653–688
Rao C, Toutenburg H (1995) Linear models: least squares and alternatives, 2nd edn. Springer, New York
Sarkar N (1992) A new estimator combining the ridge regression and the restricted least squares methods of estimation. Commun Stat Theory Methods 21:1987–2000
Sarkar N (1996) Mean square error matrix comparison of some estimators in linear regressions with multicollinearity. Stat Probab Lett 30:133–138
Sarkar N, Chandra S (2012) Comparison of the \({r-(k, d)}\) class estimator with some estimators under the Mahalanobis loss function, mimeo. www.isical.ac.in/~eru/papers
Theil H, Goldberger AS (1961) On pure and mixed statistical estimation in economics. Int Econ Rev 2:65–78
Trenkler G (1984) On the performance of biased estimators in the linear regression model with correlated or heteroscedastic errors. J Econom 25:179–190
Yang H, Wu J (2011) A stochastic restricted \({k-d}\) class estimator, Statistics, 1–8
Xu J, Yang H (2011) On the restricted \({r-k}\) class estimator and the restricted \({r-d}\) class estimator in linear regression. J Stat Comput Simul 81(6):679–691
Acknowledgments
The authors are thankful to the editor and the reviewers for their valuable comments and suggestions which have led to substantial improvement in the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was carried out when the first author was a visiting scientist at Indian Statistical Institute, North-East Center, Tezpur, Assam, India, during July 2011–June 2012.
Rights and permissions
About this article
Cite this article
Chandra, S., Sarkar, N. A restricted \(r{-}k\) class estimator in the mixed regression model with autocorrelated disturbances. Stat Papers 57, 429–449 (2016). https://doi.org/10.1007/s00362-015-0664-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00362-015-0664-4
Keywords
- \(r{-}k\) class estimator
- Mixed regression estimator
- Stochastic linear restrictions
- Autocorrelated errors