Abstract
Model-based clustering of human population genomic data, composed of 1,318 individuals arisen from western Central Africa and 160,470 markers, is considered. This challenging analysis leads us to develop a new methodology for variable selection in clustering. To explain the differences between subpopulations and to increase the accuracy of the estimates, variable selection is done simultaneously to clustering. We proposed two approaches for selecting variables when clustering is managed by the latent class model (i.e., mixture considering independence within components). The first method simultaneously performs model selection and parameter inference. It optimizes the Bayesian Information Criterion with a modified version of the standard expectation–maximization algorithm. The second method performs model selection without requiring parameter inference by maximizing the Maximum Integrated Complete-data Likelihood criterion. Although the application considers categorical data, the proposed methods are introduced in the general context of mixed data (data composed of different types of features). As the first step, the interest of both proposed methods is shown on simulated and several benchmark real data. Then, we apply the clustering method to the human population genomic data which permits to detect the most discriminative genetic markers. The proposed method implemented in the R package VarSelLCM is available on CRAN.
Similar content being viewed by others
References
Akaike, H. (1973). Information theory and an extension of the maximum likelihood principle. In Second International Symposium on Information Theory (Tsahkadsor, 1971) (pp. 267–281). Budapest: Akadémiai Kiadó.
Alexander, D.H., Novembre, J., Lange, K. (2009). Fast model-based estimation of ancestry in unrelated individuals. Genome Research, 19.
Andrews, J.L., & McNicholas, P.D. (2014). Variable selection for clustering and classification. Journal of Classification, 31(2), 136–153.
Biernacki, C., Celeux, G., Govaert, G. (2000). Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(7), 719–725.
Biernacki, C., & Maugis-Rabusseau, C. (2015). High-dimensional clustering. Choix de modèles et agrégation, Sous la direction de J-J. DROESBEKE, G. SAPORTA, C. THOMAS-AGNAN, Technip.
Biernacki, C., Celeux, G., Govaert, G. (2010). Exact and Monte Carlo calculations of integrated likelihoods for the latent class model. Journal of Statistical Planning and Inference, 140(11), 2991–3002.
Bontemps, D., & Toussile, W. (2013). Clustering and variable selection for categorical multivariate data. Electronic Journal of Statistics, 7, 2344–2371.
Bretagnolle, V. (2007). Personal communication. source: Museum.
Brown, G. (2004). Diversity in Neural Network Ensembles. The University of Birmingham.
Celeux, G., & Govaert, G. (1991). Clustering criteria for discrete data and latent class models. Journal of Classification, 8(2), 157–176.
Celeux, G., Martin-Magniette, M., Maugis-Rabusseau, C., Raftery, A.E. (2009). Comparing model selection and regularization approaches to variable selection in model-based clustering. Journal de la Societe francaise de statistique, 155(2), 57.
Chang, C., Chow, C., Tellier, L., Vattikuti, S., Purcell, S.M., Lee, J. (2015). Second-generation plink: rising to the challenge of larger and richer datasets. GigaScience, 4.
Dean, N., & Raftery, A.E. (2010). Latent class analysis variable selection. Annals of the Institute of Statistical Mathematics, 62(1), 11–35.
Dempster, A.P., Laird, N.M., Rubin, D.B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39(1), 1–38.
Flury, B., & Riedwyl, H. (1988). Multivariate Statistics: a practical approach. London: Chapman and Hall.
Fop, M., Smart, K.M., Murphy, T.B. (2017). Variable selection for latent class analysis with application to low back pain diagnosis. The Annals of Applied Statistics, 11(4), 2080–2110.
Fowlkes, E.B., Gnanadesikan, R., Kettenring, J.R. (1988). Variable selection in clustering. Journal of Classification, 5(2), 205–228.
Francois, O., Currat, M., Ray, N., Han, E., Excoffier, L., Novembre, J. (2010). Principal component analysis under population genetic models of range expansion and admixture. Molecular Biology and Evolution, 27.
Friel, N., & Wyse, J. (2012). Estimating the evidence–a review. Statistica Neerlandica, 66(3), 288–308.
Golub, T., & al. (1999). Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science, 286(5439), 531–537.
Goodman, L.A. (1974). Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika, 61(2), 215–231.
Green, P.J. (1990). On use of the em for penalized likelihood estimation. Journal of the Royal Statistical Society. Series B (Methodological), 443–452.
Hand, D.J., & Yu, K. (2001). Idiot’s Bayes — not so stupid after all?. International Statistical Review, 69(3), 385–398.
Hubert, L., & Arabie, P. (1985). Comparing partitions. Journal of classification, 2(1), 193–218.
Keribin, C. (2000). Consistent estimation of the order of mixture models. Sankhyā: The Indian Journal of Statistics Series A, 49–66.
Kettenring, J.R. (2006). The practice of cluster analysis. Journal of Classification, 23(1), 3–30.
Lawson, D.J., & Falush, D. (2012). Population identification using genetic data. Annual review of genomics and human genetics, 13.
Marbac, M., & Sedki, M. (2017). Variable selection for model-based clustering using the integrated complete-data likelihood. Statistics and Computing, 27(4), 1049–1063.
Massart, P. (2007). Concentration inequalities and model selection Vol. 6. Berlin: Springer.
Maugis, C., Celeux, G., Martin-Magniette, M. (2009a). Variable selection for clustering with Gaussian mixture models. Biometrics, 65(3), 701–709.
Maugis, C., Celeux, G., Martin-Magniette, M.-L. (2009b). Variable selection in model-based clustering: a general variable role modeling. Computational Statistics and Data Analysis, 53, 3872–3882.
McLachlan, G., & Peel, D. (2000). Finite mixture models Wiley Series in probability and statistics: applied probability and statistics. New York: Wiley-Interscience.
McLachlan, G.J., & Krishnan, T. (2008). The EM algorithm and extensions. Wiley Series in probability and statistics, second edition. Hoboken: Wiley-Interscience.
McNicholas, P. (2016a). Mixture model-based classification. Boca Raton: Chapman & Hall/CRC Press.
McNicholas, P.D. (2016b). Model-based clustering. Journal of Classification, 33 (3), 331–373.
Menozzi, P., Piazza, A., Cavalli-Sforza, L. (1978). Synthetic maps of human gene frequencies in europeans. Science, 201.
Meynet, C. (2012). Sélection de variables pour la classification non supervisée en grande dimension. PhD thesis, Paris, 11.
Novembre, J., Johnson, T., Bryc, K., Kutalik, Z., Boyko, A.R., Auton, A., Indap, A., King, K.S., Bergmann, S., Nelson, M.R., et al. (2008). Genes mirror geography within Europe. Nature, 456(7218), 98–101.
Patin, E., Lopez, M., Grollemund, R., Verdu, P., Harmant, C., Quach, H., Laval, G., Perry, G.H., Barreiro, L.B., Froment, A., et al. (2017). Dispersals and genetic adaptation of Bantu-speaking populations in Africa and North America. Science, 356(6337), 543–546.
Patterson, N., Price, A.L., Reich, D. (2006). Population Structure and Eigenanalysis. PLoS Genetics, 2.
Phillips, C. (2012). Ancestry informative markers. Siegel Jay A and Saukko, Pekka J: Encyclopedia of forensic sciences. Cambridge: Academic Press.
Price, A.L., Patterson, N.J., Plenge, R.M., Weinblatt, M.E., Shadick, N.A., Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics, 38(8), 904–909.
Pritchard, J.K., Pickrell, J.K., Coop, G. (2010). The genetics of human adaptation: Hard sweeps, soft sweeps, and polygenic adaptation. Current Biology, 20.
Pritchard, J.K., Stephens, M., Donnelly, P. (2000). Inference of population structure using multilocus genotype data. Genetics, 155(2), 945–959.
Raftery, A.E., & Dean, N. (2006). Variable selection for model-based clustering. Journal of the American Statistical Association, 101(473), 168–178.
Robert, C. (2007). The Bayesian choice: from decision-theoretic foundations to computational implementation. Berlin: Springer.
Ronan, T., Qi, Z., Naegle, K.M. (2016). Avoiding common pitfalls when clustering biological data. Science Signaling, 9, 432.
Schlimmer, J.C. (1987). Concept acquisition through representational adjustment. Department of Information and Computer Science University of California. Irvine: CA.
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6(2), 461–464.
Scrucca, L., & Raftery, A.E. (2014). clustvarsel: A Package Implementing Variable Selection for Model-based Clustering in R. (submitted to) Journal of Statistical Software.
Streuli, H. (1973). Der heutige stand der kaffeechemie. In Association Scientifique International du Cafe, 6th International Colloquium on Coffee Chemisrty, 61–72.
Tadesse, M.G., Sha, N., Vannucci, M. (2005). Bayesian variable selection in clustering high-dimensional data. Journal of the American Statistical Association, 100 (470), 602–617.
White, A., Wyse, J., Murphy, T.B. (2016). Bayesian variable selection for latent class analysis using a collapsed gibbs sampler. Statistics and Computing, 26(1-2), 511–527.
Witten, D.M., & Tibshirani, R. (2010). A framework for feature selection in clustering. Journal of the American Statistical Association, 105(490), 713–726.
Yamamoto, M., & Hwang, H. (2017). Dimension-reduced clustering of functional data via subspace separation. Journal of Classification, 34(2), 294–326.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Details on the Closed Form of the Integrated Complete-Data Log-likelihood
To compute the integrated complete-data log-likelihood, we give the value p(x∙j|g, ωj, z) for any type of data (continuous, integer, and categorical).
-
If variable j is continuous, then:
$$ p(\textbf{x}_{\bullet j}|g,\omega_{j},\textbf{z})=\left\{ \begin{array}{ll} \pi^{-n/2} \left( \frac{b_{j}^{a_{j}/2}d_{j}^{1/2}}{{\Gamma}(a_{j}/2)}\right)^{g} {\prod}_{k = 1}^{g} \frac{{\Gamma}(A_{kj}/2)}{B_{kj}^{A_{kj}}D_{kj}^{1/2}} & \text{if } \omega_{j} = 1 \\ \pi^{-n/2} \frac{b_{j}^{a_{j}}d_{j}^{1/2}}{{\Gamma}(a_{j}/2)}\frac{{\Gamma}(A_{j}/2)}{B_{j}^{A_{j}}D_{j}^{1/2}} & \text{if } \omega_{j} = 0 \end{array}\right. , $$where, Aj = n + aj, \({B_{j}^{2}}={b_{j}^{2}} + {\sum }_{i = 1}^{n} (x_{ij} - \bar {\text {x}}_{j})^{2} + \frac {(c_{j} - \bar {\text {x}}_{j})^{2}}{d_{j}^{-1} + n^{-1}}\), Dj = n + dj, \(\bar {\text {x}}_{j}=\frac {1}{n}{\sum }_{i = 1}^{n} x_{ij}\), Akj = nk + aj, \(B_{kj}^{2}={b_{j}^{2}} + {\sum }_{i = 1}^{n} z_{ik} (x_{ij} - \bar {\text {x}}_{jk})^{2} + \frac {(c_{j} - \bar {\text {x}}_{jk})^{2}}{d_{j}^{-1} + n_{k}^{-1}}\), Dkj = nk + dj, \(\bar {\text {x}}_{jk}=\frac {1}{n_{k}}{\sum }_{i = 1}^{n} z_{ik}x_{ij}\) and \(n_{k}={\sum }_{i = 1}^{n}z_{ik}\).
-
If variable j is integer, then:
$$ p(\textbf{x}_{\bullet j}|g,\omega_{j},\textbf{z})=\left\{ \begin{array}{ll} \frac{1}{{\prod}_{i = 1}^{n} {\Gamma}(x_{ij}+ 1)} \left( \frac{b_{j}^{a_{j}}}{{\Gamma}(a_{j})}\right)^{g} {\prod}_{k = 1}^{g} {\Gamma}(A_{kj})B_{kj}^{-A_{kj}} & \text{if } \omega_{j} = 1 \\ \frac{1}{{\prod}_{i = 1}^{n} {\Gamma}(x_{ij}+ 1)} \frac{b_{j}^{a_{j}}}{{\Gamma}(a_{j})} {\Gamma}(A_{j})B_{j}^{-A_{j}} & \text{if } \omega_{j} = 0 \end{array}\right. , $$where, \(A_{j}={\sum }_{i = 1}^{n} x_{ij}+a_{j}\), \(B_{j}={b_{j}^{2}} + n\), \(A_{kj}={\sum }_{i = 1}^{n} z_{ik}x_{ij}+a_{j}\) and \(B_{j}={b_{j}^{2}} + {\sum }_{i = 1}^{n}z_{ik}\).
-
If variable j is categorical with mj levels, then:
$$ p(\textbf{x}_{\bullet j}|g,\omega_{j},\textbf{z})=\left\{ \begin{array}{ll} \left( \frac{{\Gamma}\left( m_{j} a\right)}{{\Gamma}(a)^{m_{j}}} \right)^{g} \prod \limits_{k = 1}^{g} \frac{{\prod}_{h = 1}^{m_{j}}{\Gamma}\left( {\sum}_{i = 1}^{n} z_{ik}{1}_{\{x_{ij}=h\}} + a_{j}\right)}{{\Gamma}\left( {\sum}_{i = 1}^{n} z_{ik} + m_{j} a_{j}\right)} & \text{if } \omega_{j} = 1 \\ \frac{{\Gamma}\left( m_{j} a\right)}{{\Gamma}(a)^{m_{j}}} \frac{{\prod}_{h = 1}^{m_{j}}{\Gamma}\left( {\sum}_{i = 1}^{n} {1}_{\{x_{ij}=h\}} + a_{j}\right)}{{\Gamma}\left( n + m_{j} a_{j}\right)}& \text{ if } \omega_{j} = 0 \end{array}\right. . $$
Appendix B: EM Algorithm To Optimize the BIC Criterion for Data with Missing Values
The EM algorithm starts at a initial point (m[0], θ[0]) with m[0] = (g, ω[0]) randomly sampled and its iteration [r] is composed of two steps:
- E step:
-
Computation of the fuzzy partition
$$ t_{ik}^{[r]}:=\frac{\tau_{k}^{[r-1]} {\prod}_{j \in \mathbf{O}_{i}} f_{kj}(x_{ij} | \boldsymbol{\alpha}_{kj}^{[r-1]})}{{\sum}_{\ell = 1}^{g} \tau_{\ell}^{[r-1]} {\prod}_{j \in \mathbf{O}_{i}} f_{\ell j}(x_{ij} | \boldsymbol{\alpha}_{\ell j}^{[r-1]})}, $$ - M step:
-
Maximization of the expectation of the penalized complete-data log-likelihood over (ω, θ), hence m[r] = (g, ω[r]) with
$$ \omega_{j}^{[r]}=\left\{ \begin{array}{rl} 1 & \text{if } {\Delta}_{j}^{[r]} > 0 \\ 0 & \text{otherwise} \end{array}\right., \tau_{k}^{[r]}=\frac{n_{k}^{[r]}}{n} \text{ and } \boldsymbol{\alpha}^{[r]}_{jk}=\left\{ \begin{array}{rl} \boldsymbol{\alpha}^{\star [r]}_{kj} & \text{if } \omega_{j}^{[r]}= 1 \\ \tilde{\boldsymbol{\alpha}}_{kj} & \text{otherwise} \end{array}\right., $$where \({\Delta }_{j}={\sum }_{k = 1}^{g} {\sum }_{\{i: j\in \mathbf {O}_{i} \}} t_{ik}^{[r]} \left (\ln f_{kj}(x_{ij} | \boldsymbol {\alpha }^{\star [r]}_{kj})- \ln f_{1j}(x_{ij} | \tilde {\boldsymbol {\alpha }}_{1j})\right ) - (g-1)\nu _{j} c\), where \(\tilde {\boldsymbol {\alpha }}_{1j}=\text {arg max}_{\boldsymbol {\alpha }_{1j}} {\sum }_{\{i: j\in \mathbf {O}_{i} \}} \ln f_{1j}(x_{ij} | \boldsymbol {\alpha }_{1j})\) and where \(\boldsymbol {\alpha }^{\star [r]}_{kj}=\text {arg max}_{\boldsymbol {\alpha }_{1j}} {\sum }_{\{i: j\in \mathbf {O}_{i} \}}t_{ik}^{[r]} \ln f_{1j}(x_{ij} | \boldsymbol {\alpha }_{1j})\).
Appendix C: Details on the Closed Form of the Integrated Complete-Data Log-Likelihood for Data with Missing Values
To compute the integrated complete-data log-likelihood, for data with missing values, we give the value p(x∙j|g, ωj, z) for any type of data (continuous, integer, and categorical) containing missing values.
-
If variable j is continuous, then:
$$ p(\textbf{x}_{\bullet j}|g,\omega_{j},\textbf{z})=\left\{ \begin{array}{ll} \pi^{-n_{j}/2} \left( \frac{b_{j}^{a_{j}/2}d_{j}^{1/2}}{{\Gamma}(a_{j}/2)}\right)^{g} {\prod}_{k = 1}^{g} \frac{{\Gamma}(A_{kj}/2)}{B_{kj}^{A_{kj}}D_{kj}^{1/2}} & \text{if } \omega_{j} = 1 \\ \pi^{-n_{j}/2} \frac{b_{j}^{a_{j}}d_{j}^{1/2}}{{\Gamma}(a_{j}/2)}\frac{{\Gamma}(A_{j}/2)}{B_{j}^{A_{j}}D_{j}^{1/2}} & \text{if } \omega_{j} = 0 \end{array}\right. , $$where,
 , Aj = nj + aj, \({B_{j}^{2}}={b_{j}^{2}} + {\sum }_{\{i: j\in \mathbf {O}_{i} \}} (x_{ij} - \bar {\text {x}}_{j})^{2} + \frac {(c_{j} - \bar {\text {x}}_{j})^{2}}{d_{j}^{-1} + n_{j}^{-1}}\), Dj = nj + dj, \(\bar {\text {x}}_{j}=\frac {1}{n_{j}}{\sum }_{\{i: j\in \mathbf {O}_{i} \}} x_{ij}\), Akj = njk + aj, \(B_{kj}^{2}={b_{j}^{2}} + {\sum }_{\{i: j\in \mathbf {O}_{i} \}} z_{ik} (x_{ij} - \bar {\text {x}}_{jk})^{2} + \frac {(c_{j} - \bar {\text {x}}_{jk})^{2}}{d_{j}^{-1} + n_{jk}^{-1}}\), Dkj = njk + dj, \(\bar {\text {x}}_{jk}=\frac {1}{n_{jk}}{\sum }_{\{i: j\in \mathbf {O}_{i} \}} z_{ik}x_{ij}\) and \(n_{jk}={\sum }_{\{i: j\in \mathbf {O}_{i} \}}z_{ik}\).
, Aj = nj + aj, \({B_{j}^{2}}={b_{j}^{2}} + {\sum }_{\{i: j\in \mathbf {O}_{i} \}} (x_{ij} - \bar {\text {x}}_{j})^{2} + \frac {(c_{j} - \bar {\text {x}}_{j})^{2}}{d_{j}^{-1} + n_{j}^{-1}}\), Dj = nj + dj, \(\bar {\text {x}}_{j}=\frac {1}{n_{j}}{\sum }_{\{i: j\in \mathbf {O}_{i} \}} x_{ij}\), Akj = njk + aj, \(B_{kj}^{2}={b_{j}^{2}} + {\sum }_{\{i: j\in \mathbf {O}_{i} \}} z_{ik} (x_{ij} - \bar {\text {x}}_{jk})^{2} + \frac {(c_{j} - \bar {\text {x}}_{jk})^{2}}{d_{j}^{-1} + n_{jk}^{-1}}\), Dkj = njk + dj, \(\bar {\text {x}}_{jk}=\frac {1}{n_{jk}}{\sum }_{\{i: j\in \mathbf {O}_{i} \}} z_{ik}x_{ij}\) and \(n_{jk}={\sum }_{\{i: j\in \mathbf {O}_{i} \}}z_{ik}\). -
If variable j is integer, then:
$$ p(\textbf{x}_{\bullet j}|g,\omega_{j},\textbf{z}) = \left\{ \begin{array}{ll} \frac{1}{{\prod}_{\{i: j\in \mathbf{O}_{i} \}} {\Gamma}(x_{ij}+ 1)} \left( \frac{b_{j}^{a_{j}}}{{\Gamma}(a_{j})}\right)^{g} {\prod}_{k = 1}^{g} {\Gamma}(A_{kj})B_{kj}^{-A_{kj}} & \text{if } \omega_{j} = 1 \\ \frac{1}{{\prod}_{\{i: j\in \mathbf{O}_{i} \}} {\Gamma}(x_{ij}+ 1)} \frac{b_{j}^{a_{j}}}{{\Gamma}(a_{j})} {\Gamma}(A_{j})B_{j}^{-A_{j}} & \text{if } \omega_{j} = 0 \end{array}\right. , $$where, \(A_{j}={\sum }_{\{i: j\in \mathbf {O}_{i} \}}+a_{j}\), \(B_{j}={b_{j}^{2}} + n_{j}\), \(A_{kj}={\sum }_{\{i: j\in \mathbf {O}_{i} \}} z_{ik}x_{ij}+a_{j}\), \(B_{j}={b_{j}^{2}} + {\sum }_{\{i: j\in \mathbf {O}_{i} \}}z_{ik}\) and
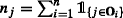 .
. -
If variable j is categorical with mj levels, then:

Rights and permissions
About this article
Cite this article
Marbac, M., Sedki, M. & Patin, T. Variable Selection for Mixed Data Clustering: Application in Human Population Genomics. J Classif 37, 124–142 (2020). https://doi.org/10.1007/s00357-018-9301-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00357-018-9301-y





 , Aj = nj + aj,
, Aj = nj + aj, 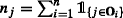 .
.