Strategic choice of sharing rules in collective contests

Abstract

Competition between groups often involves prizes that have both a public and a private component. The exact nature of the prize not only affects the strategic choice of the sharing rules determining its allocation but also gives rise to an interesting phenomenon not observed when the prize is either purely public or purely private. Indeed, we show that in the two-groups contest, for most degrees of privateness of the prize, the large group uses its sharing rule as a mean to exclude the small group from the competition, a situation called monopolization. Conversely, there is a degree of relative privateness above which the small group, besides being active, even outperforms the large group in terms of winning probabilities, giving rise to the celebrated group size paradox.

Appendix

Proof of Proposition 1

The proof relies on an extension of Ueda (2002). In order to facilitate comparison, let us transform $\alpha _i=1-{\hat{\alpha }}_i$. The expected utility of individual $k=1,\ldots ,n_i$ in group $i=A,B$ is

$$\begin{aligned} \left[ (1-{\hat{\alpha }}_i) \frac{e_{ki}}{\sum _{j=1}^{n_i} e_{ji}} p +{\hat{\alpha }}_i\frac{1}{n_i} p +(1-p) \right] \frac{E_i}{(E_A+E_B)} V -e_{ki} \end{aligned}$$

By the Kuhn–Tucker Theorem, the necessary and sufficient conditions to characterize the unique within-team symmetric pure-strategy Nash equilibrium are the following: (i) $e_{ki}= E_i/n_i$ for each member of group $i=A, B$ and (ii)

$$\begin{aligned} \frac{V}{E}\left\{ (1-{\hat{\alpha }}_i) p +\frac{{\hat{\alpha }}_i}{n_i} p +(1-p) - \frac{E_i}{E} \left[ 1- p\left( 1-\frac{1}{n_i}\right) \right] \right\} -1\le 0\quad \hbox {for all } i \end{aligned}$$

Similarly to Ueda (2002) we can define:

$$\begin{aligned} \hat{\gamma }_i= (1-{\hat{\alpha }}_i) p +\frac{{\hat{\alpha }}_i}{n_i} p+(1-p) \end{aligned}$$

We also define $\hat{n}_i= \frac{1}{1- p(1-\frac{1}{n_i})}$, which is always positive and larger than one. Then the above necessary and sufficient conditions for the pure strategy Nash equilibrium can be written as

$$\begin{aligned} \frac{V}{E}\left( \hat{\gamma }_i - \frac{E_i\hat{n}_i}{E} \right) -1\le 0\quad \hbox {for }i=A, B. \end{aligned}$$

This expression is analogous to expression (2) in Ueda (2002, p. 616), which guarantees that Proposition 1 and Corollary 1 in Ueda (2002) hold in our case. Then, in our two-groups case, from Corollary 1(b), members of group i are inactive if and only if

$$\begin{aligned} \hat{\gamma }_i \le \hat{\gamma }_j-\frac{1}{\hat{n}_i},\quad \forall i\ne j \end{aligned}$$

Rewriting this condition in terms of $\alpha _A$, $\alpha _B$ yields $\chi _i(\alpha _A,\alpha _B)\ge 0$ in Proposition 1. Further, it is immediate to see that $\chi _i(\alpha _A,\alpha _B)\ge 0$ implies $\chi _j(\alpha _A,\alpha _B)<0$. Solving the system of equations arising from the first-order conditions in the interior and corner solutions, we find the equilibrium effort levels $\tilde{e}_i, \,\tilde{e}_{j}$ and ${\hat{e}}_i$ as presented in Proposition 1 and have therefore characterized the unique within-team symmetric equilibrium.

As Baik (2008) has shown, the possibility of asymmetric equilibria may arise when groups compete for a prize that is of a pure public good nature. We shall first argue that whenever the prize includes at least some private component (i.e., $p> 0$) or when the sharing rule is partly meritocratic (i.e., $\alpha _i>0$) there exist no within-group asymmetric equilibria (i.e., equilibria where members of group i exert different effort levels). In such case, therefore, the symmetric equilibrium we characterized is unique.

Given that individuals are identical, the derivative of the expected utility with respect to $e_{ki}$ is identical for all members of group i, as it is given by

$$\begin{aligned} \frac{(E_i - e_{ki}) n_i p \alpha _i + E_j \left[ n_i + p - n_i p + (-1 + n_i) p \alpha _i\right] }{(E_i + E_j)^2 n_i} - 1 \end{aligned}$$

Thus, it follows that for any two members k and l of group i it cannot hold that $e_{ki}\ne e_{li}$ if $e_{ki}>0$ and $e_{li}>0$. Further, we can also show the non-existence of asymmetric within-group equilibria where some of the group members are inactive. If $e_{ki}=0$ for some members of group i and $e_{li}=E_i / \tilde{n}_i>0$ for the $\tilde{n}_i$ members exerting positive effort, the first order conditions require that $\frac{\partial EU_{ki}}{\partial e_{ki}} ( e_{ki}=0)\le 0$ and $\frac{\partial EU_{li}}{\partial e_{li}}=0$. One can easily verify that $\frac{\partial EU_{ki}}{\partial e_{ki}} ( e_{ki}=0)>\frac{\partial EU_{li}}{\partial e_{li}}$ for any $p>0$ and $\alpha _i>0$ and hence reject the possibility of within-group asymmetric equilibria in such cases.

• Case 1: $p>0$ and $\alpha _i>0$ for $i=A,B$

Since we have shown that for $p>0$ and $\alpha _i>0$ for $i=A,B$ there can be no within-group asymmetric equilibria, we can conclude that the characterized within-group symmetric equilibrium is the unique equilibrium.

• Case 2: $p=0$ or $p>0$ and $\alpha _i=0$ for $i=A,B$

For $p=0$ the two groups are competing for a pure public good, hence the equilibrium characterization arises directly from Baik (2008). For $p>0$ and $\alpha _i=0$ for $i=A,B$, the egalitarian distribution of the private good makes the prize equivalent to a public good with different valuation for the members of different groups. In particular, the valuation of the prize for the members of group i is equal to $V_i=(\frac{1}{n_i}+1-p)V$. By using these valuations for each group the characterization of the equilibrium also follows immediately from Baik (2008). Therefore, for $p=0$ or $p>0$ and $\alpha _i=0$ for $i=A,B$, we can follow Baik (2008) and conclude that there exist multiple within-group asymmetric equilibria, all of them characterized by the same level of aggregate effort as in the symmetric equilibrium, i.e., $E_i=n_i {\hat{e}}_i$ (substituting the corresponding value for $p=0$ or $\alpha _i=0$ for $i=A, B$).

• Case 3: $p>0$, $\alpha _i=0$ and $\alpha _j>0$

The previous extension of Ueda (2002) guarantees the existence of the within-group symmetric equilibrium. As $\alpha _j>0$, we know that there exists no within-group j asymmetric equilibrium. Then, as $\alpha _i=0$, Lemma 3 in Baik (2008) guarantees that given a within-group i symmetric equilibrium yielding aggregate effort $Ei=n_i {\hat{e}}_i >0$, any alternative distribution of individual effort within group i also constitutes an equilibrium as long as it also leads to aggregate effort $E_i=n_i {\hat{e}}_i$.

If $\alpha _j$ is such that $\chi _i(0,\alpha _j)\ge 0$, then group i is inactive and thus the equilibrium is unique and symmetric within the groups. If $\alpha _j$ is such that $\chi _i(0,\alpha _j)<0$, then both groups are active and there exist multiple within-group i asymmetric equilibria with $E_i=n_i {\hat{e}}_i$ (with the value of $\alpha _i=0$). $\square$

Proof of Proposition 2

By definition the GSP takes place if and only if $E_A<E_B$. Consider the equilibrium effort levels when both groups are active. Then $\tilde{E}_A=n_A {\hat{e}}_A<\tilde{E}_B=n_B {\hat{e}}_B$ can be written as

$$\begin{aligned} \frac{p A(\alpha _A,\alpha _B) B(\alpha _A,\alpha _B)}{C} V >0 \end{aligned}$$

where: $A(\alpha _A,\alpha _B)= - [n_B (1 - p) + p] [n_A (1-p)+ p + (n_A-1) p \alpha _A] - ( n_B-1)[n_A (1-p) + p] p \alpha _B <0$, $B(\alpha _A,\alpha _B)= n_B (1-2\alpha _A) + n_A[2 n_B (\alpha _A - \alpha _B) + 2 \alpha _B-1]$ and $C=[n_A (2 n_B (p-1) - p) - n_B p]^2 >0.$

The above expression is equal to zero for $p=0$, hence the GSP does not arise in that case. For other values of p we need to consider the sign of each expression. Since C is always positive and $A(\alpha _A,\alpha _B)$ is always negative, the GSP arises if and only if $B(\alpha _A,\alpha _B)<0$, which can be rearranged as

$$\begin{aligned} \alpha _A <\frac{n_A-n_B+2\alpha _Bn_A(n_B-1)}{2n_B(n_A-1)} \end{aligned}$$

$\square$

Proof of Proposition 3

As we have pointed out in footnote 12 maximizing the expected utility of the representative individual of group i in the within-group symmetric equilibrium also maximizes the aggregate welfare of group i. Therefore, in this proof and the subsequent ones, we focus on the sharing rule $\alpha _i$ that maximizes the expected utility of the representative individual in group i in the within-group symmetric equilibrium. We denote by ${EU}_i(\alpha _A,\alpha _B)$ the expected utility of the representative individual in group i.

From Proposition 1 and the equilibrium effort levels if both groups are active, the expected utility for the representative individual of group $i=A,B$ is given by

$$\begin{aligned} {\hat{EU}}_i(\alpha _A,\alpha _B)= & {} \frac{[n_in_j+ ((\alpha _i-1)(n_i-1)n_j+\alpha _jn_i(1-n_j))p]V}{n_i[n_jp+n_i(2n_j(1-p)+p)]^2}\\&\times [n_i(2n_i-1)n_j-Ap+B(n_i-1)p^2] \end{aligned}$$

where

$$\begin{aligned} A= & {} n_i(1-\alpha _j-n_i)+n_j(1-\alpha _i)+n_i(4n_i+\alpha _i+\alpha _j-5)n_j\\ B= & {} \alpha _i(n_j-1)+\alpha _j(n_j-1)+(n_i-1)(2n_j-1) \end{aligned}$$

From Proposition 1 and the equilibrium effort levels if only group i is active, the expected utility for group i is given by

$$\begin{aligned} {\tilde{EU}}_i(\alpha _i)= V-\frac{(n_i - 1) (n_i + \alpha _i)}{n_i^2}pV \end{aligned}$$

If group i is inactive then from Proposition 1 it must be that $\chi _i({\alpha }_i,\alpha _{j})\geqslant 0$. Notice that $\chi _i({\alpha }_i,\alpha _{j})+\chi _j({\alpha }_i,\alpha _{j})=-n_A[2 n_B(1-p) +p]-n_Bp<0$. Hence if $\chi _i({\alpha }_i,\alpha _{j})\geqslant 0$ then $\chi _j({\alpha }_i,\alpha _{j})< 0$, meaning that if i is inactive j must be active. Therefore if i is inactive it holds that $EU_i(\alpha _i)=0$.

Solving $\chi _j(\alpha _{i2}(\alpha _j),\alpha _j)= 0$ we define $\alpha _{i2}(\alpha _j) = \frac{n_i}{n_i - 1}[\frac{1-p}{p}+\frac{(n_j-1)\alpha _j+1}{n_j}]$. Given that $\chi _j(\alpha _{i},\alpha _j)$ is strictly increasing with respect to $\alpha _i$ it holds that $\chi _j(\alpha _{i},\alpha _j)>0$ for all values $\alpha _i>\alpha _{i2}(\alpha _j)$ and hence $\alpha _{i2}(\alpha _j)$ is the minimum value of $\alpha _i$ that guarantees that members of group j are inactive in equilibrium given any $\alpha _j$.

Solving $\chi _i(\alpha _{i3}(\alpha _j),\alpha _{j})=0$ we define $\alpha _{i3}(\alpha _j)=\frac{{n_j} p+{n_i}[{n_j}+{\alpha _j}p-({\alpha _j}+1) {n_j} p]}{(1-{n_i}) {n_j}p}$. Given that $\chi _i(\alpha _{i},\alpha _{j})$ is strictly decreasing with respect to $\alpha _i$ then for all ${\dot{\alpha }}_i\in [0,\alpha _{i3}(\alpha _j)]$ it is true that $\chi _i({\dot{\alpha }}_i,\alpha _{j})\geqslant 0$ and thus group i is inactive.

Comparing the expressions of $\alpha _{i2}(\alpha _j)$ and $\alpha _{i3}(\alpha _j)$ we have that $\alpha _{i2}(\alpha _j)>\alpha _{i3}(\alpha _j)$ and therefore we can write the expected utility as follows:

$$\begin{aligned} EU_i(\alpha _i)= \left\{ \begin{array}{l@{\quad }l} 0&{} \text{ if } 0\le \alpha _i\le \alpha _{i3}(\alpha _j)\\ {\hat{EU}}_i(\alpha _A,\alpha _B) &{}\text{ if } \alpha _{i3}(\alpha _j)<\alpha _i< \alpha _{i2}(\alpha _j)\\ {\tilde{EU}}_i(\alpha _i) &{}\text{ if } \alpha _i\ge \alpha _{i2}(\alpha _j) \end{array} \right. \end{aligned}$$

Notice that $EU_i(\alpha _i)$ is a continuous function since

$$\begin{aligned} \lim _{\alpha _i \rightarrow \alpha _{i3}(\alpha _j)}{\hat{EU}}_i(\alpha _A,\alpha _B)=0\quad \hbox {and}\quad \lim _{\alpha _i \rightarrow \alpha _{i2}(\alpha _j)}{\hat{EU}}_i(\alpha _A,\alpha _B)= {\tilde{EU}}_i(\alpha _i) \end{aligned}$$

Moreover, the second derivative of ${\hat{EU}}_i(\alpha _A,\alpha _B)$ is $\frac{2n_B(n_A-1)^2[n_B(p-1)-p]p^2V}{n_A[n_Bp+n_A(2n_B(1-p)+p)]^2}<0$. Thus, ${\hat{EU}}_i(\alpha _A,\alpha _B)$ is a strictly concave function in the unrestricted domain $\alpha _i\in (-\infty ,+\infty )$ and reaches a global maximum at

$$\begin{aligned}&\alpha _{i1} (\alpha _j)\\&\quad =\frac{n_j\left[ n_i (1 - p) + p\right] \left[ n_j (2 -2 n_i (1-p) - 3 p) - (n_i - 2) p\right] - (n_j - 1) (n_i - n_j) p^2 \alpha _j}{2 (n_i - 1) n_j \left[ n_j (p - 1) - p\right] p} \end{aligned}$$

Finally, notice that ${\tilde{EU}}_i(\alpha _i)$ is strictly decreasing with respect to $\alpha _i$.

If $\alpha _ {i1} (\alpha _j)\le \alpha _{i3}(\alpha _j)$ then for all $\alpha _i>\alpha _{i3}(\alpha _j)$ the expected utility $EU_i(\alpha _i)$ is strictly decreasing and hence negative. Therefore, $EU_i(\alpha _i)$ takes its maximal value of zero for all values ${\dot{\alpha }}_i\in [0,\alpha _{i3}(\alpha _j)]$. Comparing the analytical expressions of $\alpha _{i1} (\alpha _j)$ and $\alpha _{i3}(\alpha _j)$ it is true that $\alpha _{i1} (\alpha _j)\le \alpha _{i3}(\alpha _j)$ if and only if

$$\begin{aligned} \alpha _j\ge \frac{n_j}{n_j-1} \frac{n_i(1-p)+p}{p}= {\hat{\alpha }}_j \end{aligned}$$

If $\alpha _{i1} (\alpha _j)\ge \alpha _{i2}(\alpha _j)$ and given that ${\tilde{EU}}_i(\alpha _i)$ is strictly decreasing with respect to $\alpha _i$ then $EU_i(\alpha _i)$ has a unique global maximum at $\alpha _{i2}(\alpha _j)$. Comparing the analytical expressions of $\alpha _{i1} (\alpha _j)$ and $\alpha _{i2}(\alpha _j)$ it is true that $\alpha _{i1} (\alpha _j)\ge \alpha _{i2}(\alpha _j)$ if and only if

$$\begin{aligned} \alpha _j\le \frac{n_j[n_i (1-p)+3p-2]-2 p}{(n_j-1)p}={\tilde{\alpha }}_j \end{aligned}$$

If $\alpha _{i3}(\alpha _j)< \alpha _ {i1} (\alpha _j)< \alpha _{i2}(\alpha _j)$ then $EU_i(\alpha _i)$ has a unique global maximum at $\alpha _{i1} (\alpha _j)$.

Summing up, the best response of group i can be written as:

$$\begin{aligned} \alpha _i(\alpha _j)= \left\{ \begin{array}{l@{\quad }l} \alpha _{i2}(\alpha _j) &{} \text{ for } \alpha _j\le {\tilde{\alpha }}_j\\ \alpha _{i1}(\alpha _j) &{} \text{ for } {\tilde{\alpha }}_j<\alpha _j <{\hat{\alpha }}_j\\ {\dot{\alpha }}_i\in [0,\alpha _{i3}(\alpha _j)] &{} \text{ for } \alpha _j\ge {\hat{\alpha }}_j\\ \end{array} \right. \end{aligned}$$

We now consider the nine possible combinations of the two groups’ best responses:

Case 1: $i=A,B$ plays $\alpha _{i1}(\alpha _j)$

If $i=A,B$ plays $\alpha _{i1}(\alpha _j)$, it yields the following sharing rule:

$$\begin{aligned} \alpha _i=\frac{n_i}{(n_i-1)}\frac{2n_in_j(n_i-1)+A_ip+B_ip^2}{p[2n_in_j-p(n_i(2n_j-1)-n_j)]} \end{aligned}$$

where $A_i=n_in_j(9-4n_i)-n_j(n_j+2)-2n_i$ and $B_i=n_in_j(2n_i-7)+n_j(n_j+3)+3n_i-2$.

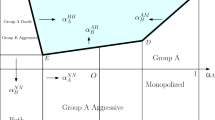
From the best responses, this is an equilibrium if and only if ${\tilde{\alpha }}_i<\alpha _i<{\hat{\alpha }}_i$ for $i=A,B$, which is true as long as

$$\begin{aligned} p>\frac{n_B(n_A-n_B-1)}{1+n_B(n_A-n_B-1)}=p_1 \end{aligned}$$

Hence, both groups being active is an equilibrium if and only if $p>p_1$.

Case 2: $i=A,B$ plays $\alpha _{i2}(\alpha _j)$

If $i=A,B$ plays $\alpha _{i2}(\alpha _j)$, there is no solution, as the best responses are two parallel lines with positive slope.

Case 3: A plays $\alpha _{A1}(\alpha _B)$ and B plays $\alpha _{B2}(\alpha _A)$

If A plays $\alpha _{A1}(\alpha _B)$ and B plays $\alpha _{B2}(\alpha _A)$, it yields the following sharing rules:

$$\begin{aligned} \alpha _A= & {} 1+n_A\left( \frac{1}{p}-1\right) \\ \alpha _B= & {} \frac{n_B[n_A(1-p)+p]}{(n_B-1)p} \end{aligned}$$

From the best responses, this is an equilibrium if and only if $\alpha _A\leqslant {\tilde{\alpha }}_A$ and ${\tilde{\alpha }}_B<\alpha _B<{\hat{\alpha }}_B$. As the sharing rules above are such that $\alpha _B>{\hat{\alpha }}_B$, the latter condition is never satisfied. Hence we do not reach an equilibrium.

Case 4: A plays $\alpha _{A2}(\alpha _B)$ and B plays $\alpha _{B1}(\alpha _A)$

If A plays $\alpha _{A2}(\alpha _B)$ and B plays $\alpha _{B1}(\alpha _A)$, it yields the following sharing rules:

$$\begin{aligned} \alpha _A= & {} \frac{n_A\left[ n_B(1-p)+p\right] }{(n_A-1)p}\\ \alpha _B= & {} 1+n_B\left( \frac{1}{p}-1\right) \end{aligned}$$

From the best responses, this is an equilibrium if and only if $\alpha _B\leqslant {\tilde{\alpha }}_B$ and ${\tilde{\alpha }}_A<\alpha _A<{\hat{\alpha }}_A$. As the sharing rules above are such that $\alpha _A>{\hat{\alpha }}_A$, the latter condition is never satisfied. Hence we do not reach an equilibrium.

Case 5: A plays $\alpha _{A1}(\alpha _B)$ and B plays ${\dot{\alpha }}_B\in [0,\alpha _{B3}(\alpha _A)]$

If A plays $\alpha _{A1}(\alpha _B)$ and B plays ${\dot{\alpha }}_B\in [0,\alpha _{B3}(\alpha _A)]$, we are at an equilibrium if and only if $\alpha _A\geqslant {\hat{\alpha }}_A$ and ${\tilde{\alpha }}_B<\alpha _B<{\hat{\alpha }}_B$, which is never satisfied. Let $\alpha _A=\alpha _{A1}(\alpha _B)$. Then, the condition $\alpha _B<\alpha _{B3}(\alpha _A)$ reduces to $\alpha _B<{\tilde{\alpha }}_B$, hence we reach a contradiction.

Case 6: A plays ${\dot{\alpha }}_A\in [0,\alpha _{A3}(\alpha _B)]$ and B plays $\alpha _{B1}(\alpha _A)$

If A plays ${\dot{\alpha }}_A\in [0,\alpha _{A3}(\alpha _B)]$ and B plays $\alpha _{B1}(\alpha _A)$, we are at an equilibrium if and only if ${\tilde{\alpha }}_A<\alpha _A<{\hat{\alpha }}_A$ and $\alpha _B\geqslant {\hat{\alpha }}_B$, which is never satisfied. Let $\alpha _B=\alpha _{B1}(\alpha _A)$. Then, the condition $\alpha _A<\alpha _{A3}(\alpha _B)$ reduces to $\alpha _A<{\tilde{\alpha }}_A$, hence we reach a contradiction.

Case 7: $i=A,B$ plays ${\dot{\alpha }}_i\in [0,\alpha _{i3}(\alpha _j)]$

If $i=A,B$ plays ${\dot{\alpha }}_i\in [0,\alpha _{i3}(\alpha _j)]$, we immediately reach a contradiction, as $\alpha _A\leqslant \alpha _{A3}(\alpha _B)$ and $\alpha _B\leqslant \alpha _{B3}(\alpha _A)$ cannot hold simultaneously. The condition $\alpha _A\leqslant \alpha _{A3}(\alpha _B)$ is equivalent to

$$\begin{aligned} \alpha _B\geqslant \frac{n_B\left[ n_A-(1-\alpha _A)(n_A-1)p\right] }{n_A(n_B-1)p} \end{aligned}$$

Then, we have that

$$\begin{aligned} \alpha _{B3}(\alpha _A)\geqslant \frac{n_B \left[ n_A-(1-\alpha _A)(n_A-1)p\right] }{n_A(n_B-1)p} \quad \hbox {if and only if }p\geqslant \frac{2n_An_B}{2n_An_B-n_A-n_B}>1 \end{aligned}$$

Hence we reach a contradiction.

Case 8: A plays $\alpha _{A2}(\alpha _B)$ and B plays ${\dot{\alpha }}_B\in [0,\alpha _{B3}(\alpha _A)]$

If A plays $\alpha _{A2}(\alpha _B)$ and B plays ${\dot{\alpha }}_B\in [0,\alpha _{B3}(\alpha _A)]$, we are at an equilibrium if and only if $\alpha _A\geqslant {\hat{\alpha }}_A$ and $\alpha _B\leqslant {\tilde{\alpha }}_B$, which holds if and only if $\alpha _B\in [ \frac{n_B (1-p)+p}{p},{\tilde{\alpha }}_B]$ and $p\leqslant p_1$.

Case 9: A plays ${\dot{\alpha }}_A\in [0,\alpha _{A3}(\alpha _B)]$ and B plays $\alpha _{B2}(\alpha _A)$

If A plays ${\dot{\alpha }}_A\in [0,\alpha _{A3}(\alpha _B)]$ and B plays $\alpha _{B2}(\alpha _A)$, we are at an equilibrium if and only if $\alpha _A\leqslant {\tilde{\alpha }}_A$ and $\alpha _B\geqslant {\hat{\alpha }}_B$, which is never satisfied. Let $\alpha _B=\alpha _{B2}(\alpha _A)$. Then, $\alpha _B\geqslant {\hat{\alpha }}_B$ reduces to $\alpha _A\geqslant [n_A(1-p)+p]/p$. As ${\tilde{\alpha }}_A<[n_A(1-p)+p]/p$, the conditions for an equilibrium are never satisfied. $\square$

Proof of Proposition 4

Clearly, if the small group is inactive, the GSP cannot occur. If $p>p_1$, from Proposition 2, the GSP arises if and only if

$$\begin{aligned} \alpha _A<\frac{n_A-n_B+2\alpha _Bn_A(n_B-1)}{2n_B(n_A-1)} \end{aligned}$$

Substituting for the equilibrium value of $\alpha _i$ ($i=A,B$) from Proposition 3, the above condition reduces to

$$\begin{aligned} \frac{(n_A-n_B)[2n_An_B(1-p)-p]}{2(n_A-1)n_Bp}<0 \end{aligned}$$

which holds if and only if $p>\frac{2 n_A n_B}{1+2 n_A n_B}=p_{GSP}$. $\square$

Proof of Proposition 5

We can obtain group i’s best response with restricted sharing rules by adding the constraint $\alpha _i\le 1$ for $i=A, B$ in the best response with unrestricted sharing rules derived in the proof of Proposition 3.

First, observe that ${\hat{\alpha }}_i>1$ for $i=A, B$ and $\forall p\in [0,1]$. Therefore, ${\dot{\alpha }}_i$ is not part of the best response with restricted sharing rules. As shown in the proof of Proposition 3, $\alpha _{i1}(\alpha _j)$ is chosen over $\alpha _{i2}(\alpha _j)$ if and only if $\alpha _{i1}(\alpha _j)< \alpha _{i2}(\alpha _j)$. By taking this into account together with the new restriction $\alpha _i\le 1$, one can write the best response for $i=A, B$ and $j\ne i$ as:

$$\begin{aligned} \alpha _i(\alpha _j)= \min \{ \alpha _{i1}(\alpha _j), \alpha _{i2}(\alpha _j), 1\} \end{aligned}$$

To find the solution we have to consider the nine combinations that arise from the previous best response. We can easily eliminate several combinations:

• If $i=A,B$ plays $\alpha _{i1}(\alpha _j)$, the sharing rule of each group is the one obtained in case 1 in the proof of Proposition 3. As the value of $\alpha _B$ always exceeds one we can discard this combination as a solution.

• If $i=A,B$ plays $\alpha _{i2}(\alpha _j)$, there is no solution, as the best responses are parallel lines (case 2 in the proof of Proposition 3).

• From cases 3 and 4 in the proof of Proposition 3, if i plays $\alpha _{i1}(\alpha _j)$ and j plays $\alpha _{j2}(\alpha _i)$, we obtain that

  $$\begin{aligned} \alpha _i=\frac{n_i[n_j(1-p)+p]}{(n_i-1)p}>1 \end{aligned}$$

  Thus, i and j playing $\alpha _{i1}(\alpha _j)$ and $\alpha _{j2}(\alpha _i)$ for $i=A, B$ and $j\ne i$ never constitutes an equilibrium.

• As $\alpha _{i2}(1)= \frac{n_B}{(n_B-1) p} > 1$ for $i=A, B$, there is no solution with i and j playing $\alpha _{i2}(\alpha _j)$ and $\alpha _j=1$ for $i=A, B$ and $j\ne i$.

• Let $\alpha _A= 1$ and $\alpha _B(\alpha _A)=\alpha _{B1}(1)$. By evaluating $\alpha _{B1}(1)$ at $p=1$ we obtain that $\alpha _B(1)= \frac{2 n_A n_B-n_A - n_B}{2 n_A(1- n_B)}>1$. Then, as $\frac{\partial \alpha _{B1}(1)}{\partial p}= -\frac{2 n_B (n_A + p - n_A p)^2 + (n_A - n_B)p^2}{2 p^2 (n_A + p - n_A p)^2} <0$ for all $p\in (0,1]$, it follows that $\alpha _{B1}(1)>1$ for any $p \in [0,1].$

After eliminating the previous seven combinations we are now left with the two cases where $\alpha _B =1$ and $\alpha _A=\min \{\alpha _{A1}(1),1\}$. By substitution of $\alpha _B=1$ we obtain the analytical value of $\alpha _{A1}(1)$:

$$\begin{aligned}&\alpha _{A1}(1) \\&\quad =\frac{n_A^2 n_B [2 n_B (1 - p) +p](1 - p) - n_B p [2 n_B (1 - p) + p] - n_A [2 n_B (1 - 2 p) p + p^2 + n_B^2 (2 + p (5 p - 7))]}{2 (n_A - 1) n_B[n_B (1 - p) + p]p} \end{aligned}$$

Solving $\alpha _{A1}(1)=1$ with respect to p yields

$$\begin{aligned} p_{1,2}= & {} \frac{1}{2}\left\{ \frac{n_A n_B [2 - 5 n_B + n_A ( 4 n_B-1)]}{n_B + n_A [n_B [2 - 3 n_B + n_A (2 n_B-1)]-1]}\right. \\&\left. \pm \,\, \sqrt{\frac{n_A n_B^2 [8 n_B + n_A [n_A^2 + (n_B - 12) n_B + 2 n_A (2 + n_B)-4]]}{[n_B + n_A [n_B (2 - 3 n_B + n_A ( 2 n_B-1))-1]]^2}}\right\} \end{aligned}$$

As $p_1$ (with the plus sign) is larger than one, we further ignore it. Thus we let $\mathring{p}=p_2<1$ be the relevant value such that $\alpha _{A1}(1)=1$. As $\frac{\partial \alpha _{A1}(1)}{\partial p}= \frac{p^2 (n_A - n_B) - 2 n_A (n_B + p - n_B p)^2}{p^2 2 (n_B + p - n_B p)^2} <0$ for all $p\in (0,1]$, it follows that $\alpha _{A1}(1)>1$ for any $p \in [0,\mathring{p})$. Therefore, at the unique equilibrium we have

• $\alpha _A=\alpha _B= 1$ for $p \in (0,\mathring{p}]$

• $\alpha _A=\alpha _{A1}(1)$ and $\alpha _B= 1$ for $p \in (\mathring{p},1].$

Substituting these equilibrium values in the relevant expression obtained in Proposition 1, we find that $\chi _i(\alpha _A,\alpha _B)<0$ for $i=A, B$ and for all $p\in (0,1]$. Hence in equilibrium both groups are active. $\square$

Proof of Proposition 6

From Proposition 2, for any $p \in (0,1]$ the GSP arises if and only if $\alpha _A<\frac{n_A-n_B+2\alpha _Bn_A(n_B-1)}{2n_B(n_A-1)}$. We know from Proposition 5 that $\alpha _A=\alpha _B=1$ for $p\in (0,\mathring{p}]$, hence the GSP arises if and only if $\frac{n_A - n_B}{ n_A n_B-n_B} < 0$ which never holds given that $n_A> n_B$.

For $p\in (\mathring{p},1]$ we know that $\alpha _B=1$ and $\alpha _A=\alpha _{A1}(1)$. Taking the equilibrium value of $\alpha _A(1)$ for $p=1$ yields $\alpha _A(1)=\frac{ 2 n_A n_B-n_A - n_B }{2 n_B( n_A-1)}$. From Proposition 2, the GSP arises at $p=1$ if and only if $\frac{ 2 n_A n_B-n_A - n_B }{2 n_B( n_A-1)}<\frac{n_A-n_B+2 n_A(n_B-1)}{2n_B(n_A-1)}$ which never holds given that $n_A>n_B$. Thus, the GSP does not arise at $p=1$. As we have shown that $\frac{\partial \alpha _{A1}(1)}{\partial p} <0$ for all $p\in (0,1]$, it follows that the GSP does not arise for any $p \in (\mathring{p},1)$. $\square$