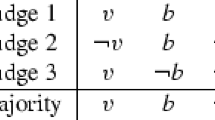Abstract
The new field of judgment aggregation aims to merge many individual sets of judgments on logically interconnected propositions into a single collective set of judgments on these propositions. Judgment aggregation has commonly been studied using classical propositional logic, with a limited expressive power and a problematic representation of conditional statements (“if P then Q ”) as material conditionals. In this methodological paper, I present a simple unified model of judgment aggregation in general logics. I show how many realistic decision problems can be represented in it. This includes decision problems expressed in languages of standard propositional logic, predicate logic (e.g. preference aggregation problems), modal or conditional logics, and some multi-valued or fuzzy logics. I provide a list of simple tools for working with general logics, and I prove impossibility results that generalise earlier theorems.
Similar content being viewed by others
References
Bovens L, Rabinowicz W (2004) Democratic answers to complex questions – an epistemic perspective. Synthese (forthcoming)
Brennan G (2001) Collective coherence?. Int Rev Law Econ 21(2):197–211
Chapman B (1998) More easily done than said: rules, reason and rational social choice. Oxford J Legal Stud 18:293–329
Chapman B (2002) Rational aggregation. Polit Philos Econ 1(3):337–354
Dietrich F (2004) Judgment aggregation: (im)possibility theorems. J Econ Theory (forthcoming)
Dietrich F (2005) The possibility of judgment aggregation for network agendas. Working paper, University of Konstanz
Dietrich F, List C (2004a) Strategy-proof judgment aggregation. Working paper, London School of Economics
Dietrich F, List C (2004b) A liberal paradox for judgment aggregation. Working paper, London School of Economics
Dietrich F, List C (2005) Judgment aggregation by Quota Rules. Working paper, London School of Economics
Dokow E, Holzman R (2005) Aggregation of binary relations. Working paper, Technion Israel Institute of Technology
Gärdenfors P (2004) An arrow-like theorem for voting with logical consequences. Working paper, Lund University
Gekker R (2003) A probability-based doxastic logic. Working paper, Department of Economics, NUI, Galway
Hintikka J (1971) Some main problems of deontic logic. In: Hilpinen R (eds). Deontic logic: introductory and systematic readings. D. Reidel, Dordrecht, pp. 59–104
Kornhauser LA, Sager LG (1986) Unpacking the court. Yale Law J 96:82–117
Kripke S (1963) Semantical analysis of modal logic I: Normal propositional calculi. Zeitschrift für mathematische Logik und Grundlagen der Mathematik 9:67–96
Lewis D (1973) Counterfactuals. Basil Blackwell, Oxford
List C (2003) A possibility theorem on aggregation over multiple interconnected propositions. Math Soc Sci 45(1):1–13
List C (2004a) The probability of inconsistencies in complex collective decisions. Soc Choice Welfare (forthcoming)
List C (2004b) A model of path dependence in decisions over multiple propositions. Am Polit Sci Rev 98(3):495–513
List C, Pettit P (2002) Aggregating sets of judgments: an impossibility result. Econ Philos 18:89–110
List C, Pettit P (2004) Aggregating sets of judgments: two impossibility results compared. Synthese 140(1–2):207–235
Mendelssohn E (1979) Introduction to mathematical logic. D. Van Nostrand
Mongin P (2005) Factoring out the impossibility of logical aggregation. Working paper, CNRS, Paris
Nehring K (2003) Arrow’s theorem as a corollary. Econ Lett 80:379–382
Nehring K, Puppe C (2002) Strategy-proof social choice on single-peaked domains: possibility, impossibility and the space between. Working paper, University of California at Davies
Nehring K, Puppe C (2004) Consistent judgement aggregation: a characterization. Working paper, University of Karlsruhe
Pauly M, van Hees M (2004) Logical constraints on judgment aggregation. J Philos Logic (forthcoming)
Pettit P (2001) Deliberative democracy and the discursive dilemma. Philos Issues 11:268–299
Pigozzi G (2004) Collective decision-making without paradoxes: an argument-based account. Working paper, King’s College, London
Priest G (2001) An introduction to non-classical logic. Cambridge University Press, Cambridge
Stalnaker R (1968): A theory of conditionals. In: Rescher N. (eds). Studies in logical theory. Blackwell, Oxford
van Hees M (2004) The limits of epistemic democracy. Working paper, University of Groningen
Wagner Decew J (1981) Conditional obligation and counterfactuals. J Philos Logic 10(1):55–72
Wilson R (1975) On the theory of aggregation. J Econ Theory 10:89–99
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dietrich, F. A generalised model of judgment aggregation. Soc Choice Welfare 28, 529–565 (2007). https://doi.org/10.1007/s00355-006-0187-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-006-0187-y