A functional error analysis of differential optical flow methods

Abstract

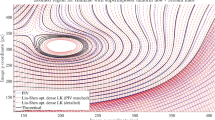
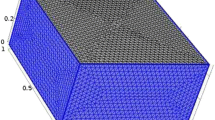
We analyze the sources of error in differential optical flow methods using techniques for the analysis of partial differential equations. We first derive an a priori error bound for the estimated optical flow field. We then systematically interpret this error bound and show that the estimation error is primarily bounded by the best-fit approximation error—which quantifies the fidelity with which one can represent the true optical flow field by a chosen or learned set of basis functions—divided by a stability constant—which quantifies one’s ability to infer the optical flow field given the information content of the acquired data. We also show that the estimation error is bounded by effects associated with the finite temporal and spatial resolution of the acquired data. In particular, we show that the main finite resolution effects are related to the finite differencing and time averaging of the measured intensity fields. Finally, we demonstrate the error bound numerically using synthetic three-dimensional data sets based on direct numerical simulations of homogeneous isotropic turbulence and transitional boundary layer flow provided by Johns Hopkins University (Li et al. in J Turbul 9:N31, 2008; Zaki in Flow Turbul Combust in 91(3):451–473, 2013).

Graphic abstract

A Proof of a priori error bound

A.1 Key lemmas

Before we prove error bound (8), we state four key lemmas required for the proof.

Lemma 1

(Midpoint rule error bound) For all twice differentiable $f: \varOmega \rightarrow \mathbb {R}$,

$$\begin{aligned} \left| \int _\varOmega f \text {d}\underline{x}- \int _{\varOmega ,h} f \text {d}\underline{x}\right| \le c_{\rm q} h^2 \Vert D^2 f \Vert _{L^{\infty }(\varOmega )}, \end{aligned}$$

for some $c_{\rm q}$ independent of h.

Proof

See Theorem 8.5 of (Ern and Guermond 2010). $\square$

Lemma 2

(Filter error bound) For any twice differentiable $I(\cdot ,t) : \varOmega \rightarrow \mathbb {R}$,

$$\begin{aligned} \Vert I(\cdot ,t) - \varPi _h * I(\cdot ,t) \Vert _{L^\infty (\varOmega )} \le c_{\rm f} h^2 \Vert D^2 I(\cdot ,t) \Vert _{L^{\infty }(\varOmega )} \end{aligned}$$

for some $c_{\rm f}$ independent of h.

Proof

We first introduce an $n_\mathrm {d}$-cube centered about $\underline{x}$, $\omega (\underline{x}) \,{:}=\,\underline{x} + (-h/2,h/2)^{n_\mathrm {d}}$. We then note that by the definition of the rectangular filter, for any $\underline{x} \in \varOmega$ and $t \in T$,

$$\begin{aligned}&\bigg | I(\underline{x},t) - \frac{1}{\mu (\omega (\underline{x}))} \int _{\omega (\underline{x})} I(\underline{y},t) \text {d}\underline{y}\bigg | \\&\quad =\frac{1}{\mu (\omega (\underline{x}))} \bigg | \int _{\omega (\underline{x})} I(\underline{y},t) \text {d}\underline{y}- \mu (\omega (\underline{x})) I(\underline{x},t) \bigg |\\&\quad \le \frac{1}{\mu (\omega (\underline{x}))} c_{\rm f} h^2 \mu (\omega (\underline{x})) \Vert D^2I(\cdot ,t)\Vert _{L^{\infty }(\omega (\underline{x}))} \\&\quad = c_{\rm f} h^2 \Vert D^2I(\cdot ,t)\Vert _{L^{\infty }(\omega (\underline{x}))}, \end{aligned}$$

where $\mu (\omega (\underline{x}))$ denotes the measure of $\omega (\underline{x})$, and the inequality follows from Lemma 8.4 of (Ern and Guermond 2010). $\square$

Lemma 3

(Time-averaged finite difference error bound) Let $t^\star \,{:}=\,t_0 + \varDelta t/2$ be the midpoint time in T. For any three-times differentiable $I : \varOmega \times T \rightarrow \mathbb {R}$,

$$\begin{aligned}&\Vert {\underline{\nabla }}I(\cdot ,t^*) - \overline{{\underline{\nabla }}}_h I \Vert _{L^\infty (\varOmega )}\\&\quad \le c_{\rm t} \varDelta t^2 \Vert \partial _t^2 {\underline{\nabla }}I \Vert _{L^\infty (\varOmega \times T)} + c_{\rm fdx} h^2 \Vert D^3 I \Vert _{L^\infty (\varOmega \times T)} \end{aligned}$$

for some constants $c_{\rm t}$ and $c_{\rm fdx}$ independent of h and $\varDelta t$.

Proof

We first decompose the error as

$$\begin{aligned}&\Vert {\underline{\nabla }}I(\cdot ,t^\star ) - \overline{{\underline{\nabla }}}_h I \Vert _{L^\infty (\varOmega )}\\&\quad \le \Vert {\underline{\nabla }}I(\cdot ,t^\star ) - \overline{{\underline{\nabla }}}I \Vert _{L^\infty (\varOmega )} + \Vert \overline{{\underline{\nabla }}}I - \overline{{\underline{\nabla }}}_h I \Vert _{L^\infty (\varOmega )}, \end{aligned}$$

where $\overline{{\underline{\nabla }}}I \,{:}=\,({\underline{\nabla }}I(\cdot , t_0) + {\underline{\nabla }}I(\cdot , t_0 + \varDelta t))/2$ is the time-averaged gradient. To bound the first term, we note that the time averaging is equivalent to evaluating the linear interpolant at the midpoint time $t^\star$. Hence,

$$\begin{aligned} \Vert {\underline{\nabla }}I(\cdot ,t^\star ) - \overline{{\underline{\nabla }}}I \Vert _{L^\infty (\varOmega )} \le c_{\rm t} \varDelta t^2 \Vert \partial _t^2 {\underline{\nabla }}I \Vert _{L^\infty (\varOmega \times T)}. \end{aligned}$$

To bound the second term, we note that the error in the centered finite difference is bounded by

$$\begin{aligned} \Vert \overline{{\underline{\nabla }}}I - \overline{{\underline{\nabla }}}_h I \Vert _{L^\infty (\varOmega )} \le c_{\rm fdx} h^2 \Vert D^3 I \Vert _{L^\infty (\varOmega \times T)}. \end{aligned}$$

The application of the time-averaging and finite difference bounds to the error decomposition yields the desired result. $\square$

Lemma 4

(Temporal finite difference error bound) Let $t^\star \,{:}=\,t_0 + \varDelta t/2$ be the midpoint time in T. For any $I : \varOmega \times T \rightarrow \mathbb {R}$ that is three-times differentiable in time,

$$\begin{aligned} \Vert \partial _t I(\cdot ,t^*) - \partial _{t,\varDelta t} I\Vert _{L^\infty (\varOmega )} \le c_{\rm fdt} \varDelta t^2 \Vert \partial _t^3 I \Vert _{L^\infty (\varOmega \times T)}, \end{aligned}$$

for some $c_{\rm fdt}$ independent of $\varDelta t$.

Proof

This is a standard centered difference error bound. $\square$

A.2 Problem statement

As stated in Sect. 2.2, the estimated OF field $\underline{u}_\delta \in \mathcal{W}_n$ is given by

$$\begin{aligned} \underline{u}_\delta = {{\,{\rm arg\,min}\,}}_{\underline{w}_\delta \in \mathcal{W}_n} \int _{\varOmega ,h} (\partial _{t,\varDelta t} I_h + \overline{\underline{\nabla }}_h I_h \cdot \underline{w}_\delta )^2 \text {d}\underline{x}. \end{aligned}$$

We note that $\underline{u}_\delta$ is the solution to the following Petrov–Galerkin problem: Find $\underline{u}_\delta \in \mathcal{W}_n$ such that

$$\begin{aligned} a_\delta (\underline{u}_\delta , v_\delta ) = \ell _\delta (v_\delta ) \quad \forall v_\delta \in \mathcal{V}_\delta , \end{aligned}$$

where $\mathcal{V}_\delta {:}{=}\{ v \ \mid \ v = \overline{\underline{\nabla }}_h I_h \cdot \underline{w}_n, \forall \underline{w}_n \in \mathcal{W}_n \}$ and

$$\begin{aligned} a_\delta (\underline{w},v)&{:}{=}\int _{\varOmega ,h} v \overline{\underline{\nabla }}_h I_h \cdot \underline{w}\text {d}\underline{x}\quad \forall \underline{w}\in \mathcal{W}, \forall v \in \mathcal{V}, \\ \ell _\delta (v)&{:}{=}\int _{\varOmega ,h} v \partial _{t,\varDelta t} I_h \text {d}\underline{x}\quad \forall v \in \mathcal{V}. \end{aligned}$$

We now assume that the true OF field $\underline{u} \in \mathcal{W}\,{:}=\,H(\text {div};\varOmega )$ satisfies

$$\begin{aligned} a(\underline{u},v) = \ell (v) \quad \forall v \in \mathcal{V}\,{:}=\,L^2(\varOmega ), \end{aligned}$$

where

$$\begin{aligned} a(\underline{w},v)&\,{:}=\,\int _\varOmega v \underline{\nabla }I(\underline{x}, t^*) \cdot \underline{w}\text {d}\underline{x}\quad \forall \underline{w}\in \mathcal{W}, \forall v \in \mathcal{V}, \\ \ell (v)&\,{:}=\,\int _\varOmega v \partial _t I(\underline{x}, t^*) \text {d}\underline{x}\quad \forall v \in \mathcal{V}, \end{aligned}$$

and $t^\star \,{:}=\,t_0 + \varDelta t/2$.

We wish to bound the estimation error $\Vert \underline{u} - \underline{u}_\delta \Vert _{\mathcal{W}}$.

A.3 A priori error estimate

To bound the estimation error, we first recall the Petrov–Galerkin error bound (e.g., Ern and Guermond 2010):

$$\begin{aligned}&\Vert \underline{u} - \underline{u}_\delta \Vert _{\mathcal{W}} \le \inf _{w_\delta \in \mathcal{W}_n} \Big [ \underbrace{ ( 1+ \frac{\gamma }{\alpha _{\delta }}) \Vert \underline{u} - \underline{w}_\delta \Vert _{\mathcal{W}} }_{\text {(I)}} \nonumber \\&\quad + \frac{1}{\alpha _{\delta }} \sup _{v_\delta \in \mathcal{V}_n} \underbrace{ \frac{|a(\underline{w}_\delta ,v_\delta ) - a_\delta (\underline{w}_\delta ,v_\delta )|}{\Vert v_\delta \Vert _{\mathcal{V}}} }_{\text {(II)}}\Big ] \nonumber \\&\quad + \frac{1}{\alpha _{\delta }} \sup _{v_\delta \in \mathcal{V}_n} \underbrace{\frac{|\ell (v_\delta ) - \ell _\delta (v_\delta )|}{\Vert v_\delta \Vert _{\mathcal{V}}} }_{\text {(III)}}. \end{aligned}$$

(11)

We now analyze terms (I)–(III) individually.

Let us begin with (I). Here we seek a bound for the stability constant $\alpha _\delta$ defined as (e.g., Ern and Guermond 2010)

$$\begin{aligned} \alpha _\delta {:}{=}\inf _{\underline{w}\in \mathcal{W}_n} \sup _{v \in \mathcal{V}_n} \frac{a_\delta (\underline{w},v)}{\Vert \underline{w}\Vert _{\mathcal{W}}\Vert v \Vert _{\mathcal{V}}}, \end{aligned}$$

We note that the continuity constant $\gamma$ is defined as (e.g., Ern and Guermond 2010)

$$\begin{aligned} \gamma {:}{=}\sup _{\underline{w}_n \in \mathcal{W}} \frac{\Vert {\underline{\nabla }}I \cdot \underline{w}_n\Vert _{L^2(\varOmega )}}{\Vert \underline{w}_n \Vert _{\mathcal{W}}} \end{aligned}$$

and, as such, is dictated by the information content of the acquired data; it does not depend on the particular OFME method used and serves only to rescale the parameter-dependent stability constant.

Before we continue with our analysis, we clarify three points regarding the notation that we use in the remainder of this proof. First, for the sake of notational convenience, we let $\hat{D}^Q f$ be the collection of functions $f,Df, \ldots ,D^Qf$ satisfying the identity

$$\begin{aligned} \Vert \hat{D}^Q f\Vert _{L^\infty (\varOmega )} \equiv \max _{0 \le q \le Q} \Vert D^q f\Vert _{L^\infty (\varOmega )}. \end{aligned}$$

Second, we introduce the simplifying notation ${I^\star }\,{:}=\,I(\cdot ,t^*)$. Third, the bounding coefficients $c_q$ and C are generic and, hence, reused in multiple inequalities.

We now return to our analysis. By the definition of $a_\delta (\cdot ,\cdot )$ and the fact that $\Vert \cdot \Vert _{\mathcal{V}}\equiv \Vert \cdot \Vert _{L^2(\varOmega )}$, $\alpha _\delta$ specializes to

$$\begin{aligned} \alpha _\delta = \inf _{\underline{w}\in \mathcal{W}_n} \sup _{v \in \mathcal{V}_n} \frac{\int _{\varOmega ,h} v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}}{\Vert \underline{w}\Vert _{\mathcal{W}}\Vert v \Vert _{L^2(\varOmega )}}. \end{aligned}$$

Because term (III) is divided by $\alpha _\delta$, we wish to bound $\alpha _\delta$ from below so that $1/\alpha _\delta$ is bounded from above.

We note that the error due to the quadrature is bounded by

$$\begin{aligned}&\left| \int _{\varOmega } v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}- \int _{\varOmega ,h} v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}\right| \nonumber \\&\quad \le c_q h^2 \Vert D^2 (v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}) \Vert _{L^2(\varOmega )}\nonumber \\&\quad \le C h^2 \sum _{q=0}^2 \Vert D^{q} \overline{{\underline{\nabla }}}_h I_h \Vert _{L^{\infty }(\varOmega )} \Vert D^{2-q}(\underline{w}v) \Vert _{L^2(\varOmega )}\nonumber \\&\quad \le C h^2 \Vert \hat{D}^2 \overline{{\underline{\nabla }}}_h I_h \Vert _{L^{\infty }(\varOmega )} \Vert \hat{D}^2 \underline{w}\Vert _{L^4(\varOmega )} \Vert \hat{D}^2 v \Vert _{L^4(\varOmega )}\nonumber \\&\quad \le c_{\rm q,0} h^2 \Vert \hat{D}^2 \overline{{\underline{\nabla }}}_h I_h \Vert _{L^{\infty }(\varOmega )} \Vert \underline{w}\Vert _{\mathcal{W}} \Vert v \Vert _{L^2(\varOmega )}. \end{aligned}$$

(12)

Here the first inequality follows from the quadrature error bound (Lemma 1); the second inequality follows from Hölder’s inequality; the third inequality follows from Schwarz inequality; and the last inequality follows from the equivalence of norms of functions in polynomial spaces $\mathcal{W}_n$ and $\mathcal{V}_\delta$. It hence follows that

$$\begin{aligned} \alpha _\delta =&\inf _{\underline{w}\in \mathcal {W}_n} \sup _{v \in \mathcal {V}_n} \Bigg ( \frac{\int _{\varOmega } v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}}{\Vert \underline{w}\Vert _{\mathcal{W}}\Vert v \Vert _{L^2(\varOmega )}}\\&- \frac{ \int _{\varOmega } v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}- \int _{\varOmega ,h} v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}}{\Vert \underline{w}\Vert _{\mathcal{W}}\Vert v \Vert _{L^2(\varOmega )}} \Bigg )\\ \ge&\inf _{\underline{w}\in \mathcal {W}_n} \sup _{v \in \mathcal {V}_n} \frac{\int _{\varOmega } v \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\text {d}\underline{x}}{\Vert \underline{w}\Vert _{\mathcal{W}}\Vert v \Vert _{L^2(\varOmega )}} - c_\mathrm{q,0} h^2 \Vert \hat{D}^2 \overline{{\underline{\nabla }}}_h I_h \Vert _{L^{\infty }(\varOmega )}\\ =&\inf _{\underline{w}\in \mathcal {W}_n} \frac{ \Vert \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\Vert _{L^2(\varOmega )} }{\Vert \underline{w}\Vert _{\mathcal{W}}} - c_\mathrm{q,0} h^2 \Vert \hat{D}^2 \overline{{\underline{\nabla }}}_h I_h \Vert _{L^{\infty }(\varOmega )}\\ =&\inf _{\underline{w}\in \mathcal {W}_n} \frac{ \Vert \overline{{\underline{\nabla }}}_h I_h \cdot \underline{w}\Vert _{L^2(\varOmega )} }{\Vert \underline{w}\Vert _{\mathcal{W}}} - O(h^2). \end{aligned}$$

Here the first inequality follows from the substitution of (12) to the second term, and the second to last equality follows from choosing $v = \overline{\underline{\nabla }}_h I_h \cdot \underline{w}$.

We next analyze (II). We first decompose the term as

$$\begin{aligned} \text {(II)}&= \frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \left( \int _\varOmega v \underline{\nabla }{I^\star }\cdot \underline{w}\text {d}\underline{x}- \int _{\varOmega ,h} v \overline{\underline{\nabla }}_h I_h \cdot \underline{w}\text {d}\underline{x}\right) \\&= \frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \underbrace{ \left( \int _\varOmega v \underline{\nabla }{I^\star }\cdot \underline{w}\text {d}\underline{x}- \int _{\varOmega ,h} v \underline{\nabla }{I^\star }\cdot \underline{w}\text {d}\underline{x}\right) }_{\text {(II.1)}} \\&\quad +\frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \underbrace{ \left( \int _{\varOmega ,h} v \underline{\nabla }{I^\star }\cdot \underline{w}\text {d}\underline{x}- \int _{\varOmega ,h} v \overline{\underline{\nabla }}_h I_h \cdot \underline{w}\text {d}\underline{x}\right) }_{\text {(II.2)}} . \end{aligned}$$

Term (II.1) is the error due to the quadrature and is bounded by

$$\begin{aligned} \text {(II.1)}&\le c_q h^2 \Vert D^2 (v {\underline{\nabla }}{I^\star }\cdot \underline{w}) \Vert _{L^2(\varOmega )}\\&\le C h^2 \sum _{q=0}^2 \Vert D^{q+1} {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert D^{2-q}(\underline{w}v) \Vert _{L^2(\varOmega )}\\&\le C h^2 \Vert \hat{D}^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert \hat{D}^2 \underline{w}\Vert _{L^4(\varOmega )} \Vert \hat{D}^2 v \Vert _{L^4(\varOmega )}\\&\le c_{\rm q,1} h^2 \Vert \hat{D}^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert \underline{w}\Vert _{L^2(\varOmega )} \Vert v \Vert _{L^2(\varOmega )}. \end{aligned}$$

Here the first inequality follows from the quadrature error bound (Lemma 1); the second inequality follows from Hölder’s inequality; the third inequality follows from Schwarz inequality; and the last inequality follows from the equivalence of norms of functions in polynomial spaces $\mathcal{W}_n$ and $\mathcal{V}_\delta$.

To bound (II.2), we first note that

$$\begin{aligned}&\Vert {\underline{\nabla }}{I^\star }- \overline{{\underline{\nabla }}}_h I_h \Vert _{L^\infty (\varOmega )} = \Vert {\underline{\nabla }}{I^\star }- \overline{{\underline{\nabla }}}_h (\varPi _h * I) \Vert _{L^\infty (\varOmega )}\\&\quad = \Vert {\underline{\nabla }}{I^\star }- \varPi _h * (\overline{{\underline{\nabla }}}_h I) \Vert _{L^\infty (\varOmega )}\\&\quad \le \Vert {\underline{\nabla }}{I^\star }- \varPi _h * {\underline{\nabla }}{I^\star }\Vert _{L^\infty (\varOmega )} + \Vert \varPi _h * ( {\underline{\nabla }}{I^\star }- \overline{{\underline{\nabla }}}_h I) \Vert _{L^\infty (\varOmega )}\\&\quad \le \Vert {\underline{\nabla }}{I^\star }- \varPi _h * {\underline{\nabla }}{I^\star }\Vert _{L^\infty (\varOmega )} + \Vert {\underline{\nabla }}{I^\star }- \overline{{\underline{\nabla }}}_h I \Vert _{L^\infty (\varOmega )}\\&\quad \le c_{\rm f} h^2 \Vert D^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} + c_t \varDelta t^2 \Vert \partial _t^2 {\underline{\nabla }}I \Vert _{L^\infty (\varOmega \times T)}\\&\quad + c_{\rm fdx} h^2 \Vert D^3 I \Vert _{L^\infty (\varOmega \times T)} \,{:}=\,F , \end{aligned}$$

where the first equality follows from the definition of the filter; the second equality follows from the commutativity of the filter $\varPi _h*$ with the time-averaged finite difference operator $\overline{{\underline{\nabla }}}_h$; the first inequality is the triangle inequality; the second inequality follows from the property $\Vert \varPi _h* f \Vert _{L^\infty (\varOmega )} \le \Vert f \Vert _{L^\infty (\varOmega )}$ $\forall f$; and the last inequality follows from the filter error bound (Lemma 2) and the time-averaged finite difference error bound (Lemma 3). It follows that

$$\begin{aligned} (\text {II.2}) \le&F \Vert \int _{\varOmega ,h} |v \underline{w}| \text {d}\underline{x}\Vert _{\ell ^1(\mathbb {R}^d)}\\ \le&F ( 1 + c_{\rm q} h^2)\Vert \underline{w}\Vert _{L^2(\varOmega )} \Vert v \Vert _{L^2(\varOmega )} , \end{aligned}$$

where the second inequality follows from the quadrature error bound.

Combining our results for (II.1) and (II.2), we thus find that (II) is bounded by

$$\begin{aligned} (\text {II}) \le&\Big (c_{\rm q,1} h^2 \Vert \hat{D}^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} + c_{\rm f} (1 + c_{\rm q} h^2) h^2 \Vert D^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm fdx} (1 + c_{\rm q} h^2) h^2 \Vert D^3 I \Vert _{L^{\infty }(\varOmega \times T)} \nonumber \\&+ c_{\rm t} (1 + c_{\rm q} h^2) \varDelta t^2 \Vert \partial _t^2 I \Vert _{L^\infty (\varOmega \times T)} \Big ) \Vert w \Vert _{L^2(\varOmega )} \Vert v \Vert _{L^2(\varOmega )} \nonumber \\ =&\Big (c_{\rm q,1} h^2 \Vert \hat{D}^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} + c_{\rm f} h^2 \Vert D^3 {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm fdx} h^2 \Vert D^3 I \Vert _{L^{\infty }(\varOmega \times T)} + c_{\rm t} \varDelta t^2 \Vert \partial _t^2 I \Vert _{L^\infty (\varOmega \times T)} \nonumber \\&+ O(h^4) + O(h^2\varDelta t^2) \Big ) \Vert w \Vert _{L^2(\varOmega )} \Vert v \Vert _{L^2(\varOmega )}. \end{aligned}$$

(13)

This bound identifies four sources of error that are second order in h or $\varDelta t$: quadrature, filtering, spatial time difference and time averaging.

Finally, we analyze (III). We first note that

$$\begin{aligned} \text {(III)}&= \frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \left( \int _{\varOmega } v \partial _t {I^\star }\text {d}\underline{x}- \int _{\varOmega ,h} v \partial _{t,\varDelta t} I_h \text {d}\underline{x}\right) \\&=\frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \underbrace{ \left( \int _{\varOmega } v \partial _t {I^\star }\text {d}\underline{x}- \int _{\varOmega ,h} v \partial _{t} {I^\star }\text {d}\underline{x}\right) }_{\text {(III.1)}} \\&\quad + \frac{1}{\Vert v \Vert _{L^2(\varOmega )}} \underbrace{ \left( \int _{\varOmega ,h} v \partial _{t} {I^\star }\text {d}\underline{x}- \int _{\varOmega ,h} v \partial _{t,\varDelta t} I_h \text {d}\underline{x}\right) }_{\text {(III.2)}}. \end{aligned}$$

Term (III.1) is the error due to the quadrature and is bounded by

$$\begin{aligned} \text {(III.1)}&\le c_q h^2 \Vert D^2(v \partial _{t} {I^\star }) \Vert _{L^2(\varOmega )}\\&\le C h^2 \sum _{q=0}^2 \Vert D^q \partial _{t} {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert D^{2-q} v \Vert _{L^2(\varOmega )}\\&\le C h^2 \Vert \hat{D}^2 \partial _{t} {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert \hat{D}^2 v \Vert _{L^2(\varOmega )}\\&\le c_{\rm q,2} h^2 \Vert \hat{D}^2 \partial _{t} {I^\star }\Vert _{L^{\infty }(\varOmega )} \Vert v \Vert _{L^2(\varOmega )}. \end{aligned}$$

Here the first inequality follows from the quadrature error bound (Lemma 1); the second inequality follows from Hölder’s inequality; the third inequality follows from the definition of the norms; and the last inequality follows from the equivalence of norms of functions in polynomial spaces $\mathcal{W}_n$ and $\mathcal{V}_\delta$.

To bound (III.2), we first note that

$$\begin{aligned}&\Vert \partial _t {I^\star }- \partial _{t,\varDelta t} I_h \Vert _{L^\infty (\varOmega )} = \Vert \partial _t {I^\star }- \partial _{t,\varDelta t} (\varPi _h * I) \Vert _{L^\infty (\varOmega )}\\&\quad = \Vert \partial _t {I^\star }- \varPi _h * (\partial _{t,\varDelta t} I) \Vert _{L^\infty (\varOmega )}\\&\quad \le \Vert \partial _t {I^\star }- \varPi _h * \partial _t {I^\star }\Vert _{L^\infty (\varOmega )}\\&\quad + \Vert \varPi _h * ( \partial _t {I^\star }- \partial _{t,\varDelta t} I) \Vert _{L^\infty (\varOmega )}\\&\quad \le \Vert \partial _t {I^\star }- \varPi _h * \partial _t {I^\star }\Vert _{L^\infty (\varOmega )} + \Vert \partial _t {I^\star }- \partial _{t,\varDelta t} I \Vert _{L^\infty (\varOmega )}\\&\quad \le c_{\rm f} h^2 \Vert D^2 \partial _t {I^\star }\Vert _{L^{\infty }(\varOmega )} + c_{\rm fdt} \varDelta t^2 \Vert \partial _t^2 I \Vert _{L^\infty (\varOmega \times T)} \,{:}=\,G , \end{aligned}$$

where the first equality follows from the definition of the filter; the second equality follows from the commutativity of the filter $\varPi _h*$ with the temporal finite difference operator $\partial _{t,\varDelta t}$; the first inequality is the triangle inequality; the second inequality follows from the property $\Vert \varPi _h* f \Vert _{L^\infty (\varOmega )} \le \Vert f \Vert _{L^\infty (\varOmega )}$ $\forall f$; and the last inequality follows from the filter error bound (Lemma 2) and the temporal finite difference error bound (Lemma 4). It follows that

$$\begin{aligned} (\text {III.2}) \le&G \int _{\varOmega ,h} |v| \text {d}\underline{x}\le G ( 1 + c_{\rm q} h^2) \Vert v \Vert _{L^2(\varOmega )}, \end{aligned}$$

where the second inequality follows from the quadrature error bound.

Combining our results for (III.1) and (III.2), we thus find that (III) is bounded by,

$$\begin{aligned} (\text {III}) \le&\Big ( c_{\rm q,2} h^2 \Vert \hat{D}^2 \partial _t {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm f} (1 + c_{\rm q} h^2) h^2 \Vert D^2 \partial _t {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm fdt} (1 + c_{\rm q} h^2) \varDelta t^2 \Vert \partial _t^3 I \Vert _{L^\infty (\varOmega \times T)} \Big )\Vert v \Vert _{L^2(\varOmega )} \nonumber \\ =&\Big ( c_{\rm q,2} h^2 \Vert \hat{D}^2 \partial _t {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm f} h^2 \Vert D^2 \partial _t {I^\star }\Vert _{L^{\infty }(\varOmega )} \nonumber \\&+ c_{\rm fdt} \varDelta t^2 \Vert \partial _t^3 I \Vert _{L^\infty (\varOmega \times T)} \nonumber \\&+ O(h^4) + O(h^2 \varDelta t^2)\Big )\Vert v \Vert _{L^2(\varOmega )} \end{aligned}$$

(14)

This bound identifies three sources of error that are second order in either h or $\varDelta t$: quadrature, filtering and temporal time difference.

Substituting (13) and (14) into (11) and evaluating the suprema, we obtain the desired bound. $\square$