Abstract
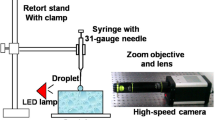
The present paper investigates experimentally the impact dynamics of crown-type splashing for miscible two- and one-component droplet wall–film interactions over a range of Weber numbers and dimensionless film thicknesses. The splashing outcome is parametrised in terms of a set of quantifiable parameters, such as crown height, top and base diameter, wall inclination, number of fingers, and secondary droplet properties. The results show that the outcome of a splashing event is not affected by the choice of similar or dissimilar fluids, provided the dimensionless film thickness is larger than 0.1. Below this threshold, distinctive features of two-component interactions appear, such as hole formation and crown bottom breakdown. The observation of different crown shapes (e.g. V-shaped, cylindrical, and truncated-cone) confirms that vorticity production induces changes in the crown wall inclination, thus affecting the evolution of the crown height and top diameter. The evolution of the crown base diameter, instead, is mainly dependent on the relative importance of liquid inertia and viscous losses in the wall-film. The maximum number of liquid fingers decreases with increasing wall, film thickness, due to the enhanced attenuation of the effect of surface properties on the fingering process. The formation of secondary droplets is also affected by changes in the crown wall inclination. In particular, for truncated-cone shapes the occurrence of crown rim contraction induces a large scatter in the secondary droplet properties. Consequently, empirical models for the maximum number and mean diameter of the secondary droplets are derived for V-shaped crowns, as observed for the hexadecane-Hyspin interactions.















Similar content being viewed by others
Abbreviations
- D :
-
Impinging drop diameter (m)
- \(D_{\text {Top}}\) :
-
Crown top diameter (m)
- \(D^{\star }_{\text {Top}}\) :
-
Non-dimensional top diameter (–)
- \(D_{\text {Base}}\) :
-
Crown base diameter (m)
- \(D^{\star }_{\text {Base}}\) :
-
Non-dimensional base diameter (–)
- \(\overline{D}_{1,0}\) :
-
Arithmetic mean diameter (m)
- \(H_{\text {CR}}\) :
-
Crown height (m)
- \(H^{\star }_{\text {CR}}\) :
-
Non-dimensional crown height (–)
- h :
-
Wall-film height (m)
- K :
-
Splashing threshold, \(We^x\ Oh^y\) (–)
- l :
-
Characteristic length (m)
- \(l_{\text {min}}\) :
-
Minimum finger height (pixel)
- \(N_{i}\) :
-
Number of drops (–)
- \(N_{\text {finger}}\) :
-
Number of liquid fingers (–)
- \(N_{\text {finger,max}}\) :
-
Maximum number of liquid fingers (–)
- \(N_{\text {drops}}\) :
-
Number of secondary droplets (–)
- \(N_{\text {drops,max}}\) :
-
Maximum number of secondary droplets (–)
- \(Oh_l\) :
-
Ohnesorge number, \(\mu\)/\(\sqrt{\rho \sigma l}\) (–)
- \(\overline{Oh}\) :
-
Averaged Ohnesorge number, \(\overline{\mu }\)/\(\sqrt{\overline{\rho } \overline{\sigma } D}\) (–)
- Re :
-
Reynolds number, \(U\ D\)/\(\nu\) (–)
- \(\overline{Re}\) :
-
Averaged Reynolds number, \(U\ D\)/\(\overline{\nu }\) (–)
- t :
-
Time (s)
- U :
-
Terminal velocity primary drop (m/s)
- \(u_{\text {drops}}\) :
-
Velocity of secondary droplets (m/s)
- \(V_{\text {rel}}\) :
-
Relative volume of ejected secondary droplets, \(V_{\text {secdrops,tot}}/V_{\text {drop,0}}\) (–)
- \(V_{\text {secdrops,tot}}\) :
-
Volume of ejected secondary droplets (m\(^3\))
- \(V_{\text {drop,0}}\) :
-
Volume of primary drop (m\(^3\))
- \(We_l\) :
-
Weber number, \(\rho U^2 l\)/\(\sigma\) (–)
- \(We_D\) :
-
Weber number primary drop, \(\rho U^2 D\)/\(\sigma\) (–)
- \(\overline{We}\) :
-
Averaged Weber number \(\overline{\rho } U^2 D\)/\(\overline{\sigma }\) (–)
- \(\alpha\) :
-
Crown inclination (\(^{\circ }\))
- \(\dot{\alpha }\) :
-
Temporal evolution of crown inclination (\(^{\circ }\))
- \(\delta\) :
-
Dimensionless film height, h / D (–)
- \(\mu\) :
-
Dynamic viscosity (Pa s)
- \(\nu\) :
-
Kinematic viscosity (mm\(^2\)/s)
- \(\rho\) :
-
Density (kg/m\(^3\))
- \(\sigma\) :
-
Surface tension (Nm\(^{-1}\))
- \(\tau\) :
-
Dimensionless time, tU/D (–)
- \(\tau _0\) :
-
Time of drop impact (s)
- \(\Omega\) :
-
Vorticity (1/s)
- a :
-
Antisymmetric
- C :
-
Constant parameter
- \({\text {ini}}\) :
-
Initial
- \({\text {max}}\) :
-
Maximum value of a parameter
- n :
-
Exponent
- s :
-
Symmetric
- f :
-
Film
References
Agbaglah G, Deegan RD (2014) Growth and instability of the liquid rim in the crown splash regime. J Fluid Mech 752:485–496
Agbaglah G, Josserand C, Zaleski S (2013) Longitudinal instability of a liquid rim. Phys Fluids 25(2):022103
Asadi A, Passandideh-Fard A (2009) A computational study of droplet impingement onto a thin liquid film. Arab J Sci Eng 34(2B):505–517
Banks D, Ajawara C, Sanchez R, Surti H, Aguilar G (2013) Effects of drop and film viscosity on drop impact onto thin films. Atom Sprays 23(6, SI):525–540
Bernard R, Foltyn P, Geppert A, Lamanna G, Weigand B (2017) Generalized analysis of the deposition/splashing limit for one- and two-component droplet impacts upon thin films. ILASS-Europe, 28th conference on liquid atomization and spray systems, Valencia, Spain
Bremond N, Villermaux E (2006) Atomization by jet impact. J Fluid Mech 549:273–306
Brevis W, Nino Y, Jirka GH (2011) Integrating cross-correlation and relaxation algorithms for particle tracking velocimetry. Exp Fluids 50(1):135–147
Cossali GE, Coghe A, Marengo M (1997) The impact of a single drop on a wetted solid surface. Exp Fluids 22:463–472
Cossali GE, Marengo M, Coghe A, Zhdanov S (2004) The role of time in single drop splash on thin film. Exp Fluids 36(6):888–900
Davidson MR (2002) Spreading of an inviscid drop impacting on a liquid film. Chem Eng Sci 57:3639–3647
Deegan RD, Brunet P, Eggers J (2008) Complexities of splashing. Nonlinearity 21:1–12
Fedorchenko AI, Wang A-B (2004) On some common features of drop impact on liquid surfaces. Phys Fluids 16(5):1349
Fujimoto H, Ogino T, Takuda H, Hatta N (2001) Collision of a droplet with a hemispherical static droplet on a solid. Int J Multiph Flow 27:1227–1245
Gao X, Li R (2015) Impact of a single drop on a flowing liquid film. Phys Rev 92(053005)
Geppert A, Chatzianagnostou D, Meister C, Gomaa H, Lamanna G, Weigand B (2016) Classification of impact morphology and splashing/deposition position limit for n-hexadecane. Atom Sprays. https://doi.org/10.1615/AtomizSpr.2015013352(26):983-1007
Geppert A, Terzis A, Lamanna G, Marengo M, Weigand B (2016b) On the formation of secondary droplets from crown bottom breakdown during drop impact on very thin films. ILASS-Europe, 27th European conference on liquid atomization and spray systems, Brighton, UK
Gregory PH, Guthrie EJ, Bunce ME (1959) Experiments on splash dispersal of fungus spores. J Gen Microbiol 20(2):328–354
Gueyffier D, Zaleski S (1998) Formation de digitations lors de l’impact d’une goutte sur un film liquide. C R Acad Sci Paris 326(Srie II b):839–844
Guo J, Dai S, Dai Q (2010) Experimental research on the droplet impacting on the liquid film. Acta Phys Sin 59:2601–2609
Guo Y, Lian Y, Sussman M (2016) Investigation of drop impact on dry and wet surfaces with consideration of surrounding air. Phys Fluids 28(073303)
Guo Y, Wei L, Liang G, Shen S (2014) Simulation of droplet impact on liquid film with CLSVOF. Int Commun Heat Mass Transf 53:26–33
Hobbs PV, Osheroff T (1967) Splashing of drops on shallow liquids. Science 158(3805):1184–1186
Huang Q, Zhang H (2008) A study of different fluid droplets impacting on a liquid film. Petrol Sci 5:62–66
Josserand C, Thoroddsen ST (2016) Drop impact on solid surface. Annual Review of Fluid Mechanics, Annual Reviews, pp 365–391
Josserand C, Zaleski S (2003) Droplet splashing on a thin liquid film. Phys Fluids 15:1650–1657
Kittel H, Roisman IV, Tropea C (2016) Outcome of drop impact onto a liquid film of different viscosities. ILASS-Europe, 27th European conference on liquid atomization and spray systems, Brighton, UK
Krechetnikov R, Homsy GH (2009) Crown-forming instability phenomena in the drop splash problem. J Colloid Interface Sci 331:555–559
Latka A, Strandburg-Peshkin M, Driscoll MM, Stevens CS, Nagel RS (2012) Creation of prompt and thin-sheet splashing by varying surface roughness or increasing air pressure. Phys Rev Lett 109(5)
Lee S, Hur N, Kang S (2011) A numerical analysis of drop impact on liquid film by using a level set method. J Mech Sci Technol 25:1–6
Liang G, Guo Y, Shen S, Yang Y (2014) Crown behavior and bubble entrainment during a drop impact on a liquid film. Theor Comput Fluid Dyn 28(2):159–170
Liang G, Mudawar I (2016) Review of mass and momentum interactions during drop impact on a liquid film. Int J Heat Mass Transf 101:577–599
Mandre S, Brenner MP (2012) The mechanism of a splash on dry solid surface. J Fluid Mech:148–172
Moreira ALN, Moita AS, Panão MR (2010) Advances and challenges in explaining fuel spray impingement: how much of single droplet impact research is useful? Prog Energy Combust Sci 36(5):554–580
Motzkus C, Gensdarmes F, Géhin E (2009) Parameter study of microdroplet formation by impact of millimetre-size droplets onto a liquid film. J Aerosol Sci 40(8):680–692
Motzkus C, Gensdarmes F, Géhin E (2011) Study of the coalescence/splash threshold of droplet impact on liquid films and its relevance in assessing airborne particle release. J Colloid Interface Sci 362(2):540–552
Mukherjee S, Abraham J (2007) Crown behavior in drop impact on wet walls. Phys Fluids 19
Okawa T, Shiraishi T, Mori T (2006) Production of secondary drops during the single water drop impact onto a plane water surface. Exp Fluids 41(6):965–974
Pan K-L, Hung C-Y (2010) Droplet impact upon a wet surface with varied fluid and surface properties. J Colloid Interface Sci 352(1):186–193
Rieber M, Frohn A (1999) A numerical study on the mechanism of splashing. Int J Heat Fluid Flow:1–7
Roisman IV (2009) Inertia dominated drop collisions. II an analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys Fluids
Roisman IV (2010) On the instability of a free viscous rim. J Fluid Mech 661:206–228
Roisman IV, Tropea C (2002) Impact of a drop onto a wetted wall: description of crown formation and propagation. J Fluid Mech 472
Roisman IV, van Hinsberg NP, Tropea C (2008) Propagation of a kinematic instability in a liquid layer: capillary and gravity effects. Phys Rev E 77(046305)
Sikalo S, Ganic EN (2006) Phenomena of droplet–surface interactions. Exp Thermal Fluid Sci 31:97–110
Thoraval M-J, Takehara K, Etoh TG, Popinet S, Ray P, Josserand C, Zaleski S, Thoroddsen ST (2012) von Kármán Vortex Street within an impacting drop. Phys Rev Lett 108(26)
Thoroddsen ST, Etoh TG, Takehara K (2006) Crown breakup by Marangoni instability. J Fluid Mech 557:63
Tropea C, Marengo M (1999) The impact of drops on walls and films. Multiph Sci Technol 11:19–36
Trujillo MF, Lee CF (2001) Modeling crown formation due to the splashing of a droplet. Phys Fluids 13(9):2503
Vander Wal RL, Berger GM, Mozes SD (2006a) Droplets splashing upon films of the same fluid of various depths. Exp Fluids 40(1):33–52
Vander Wal RL, Berger GM, Mozes SD (2006b) The combined influence of a rough surface and thin fluid film upon the splashing threshold and splash dynamics of a droplet impacting onto them. Exp Fluids 40(1):23–32
Vander Wal RL, Berger GM, Mozes SD (2006c) The splash/non-splash boundary upon a dry surface and thin fluid film. Exp Fluids 40(1):53–59
Walzel P (1980) Zerteilgrenze beim Tropfenprall. Chem Ing Tech 52:1–2
Wang A-B, Chen C-C (2000) Splashing impact of a single drop onto very thin liquid films. Phys Fluids 12(9):2155
Worthington AM (1908) A study of splashes. Longmans, Green, and Co, London
Xu L, Zhang WW, Nagel RS (2005) Drop splashing on a dry smooth surface. Phys Rev Lett 94(18)
Yarin AL (2006) Drop impact dynamics: splashing, spreading, receding, bouncing. Annu Rev Fluid Mech:1–36
Yarin AL, Weiss DA (1995) Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity. J Fluid Mech 283:1–33
Zhang LV, Brunet P, Eggers J, Deegan RD (2010) Wavelength selection in the crown splash. Phys Fluids 22:122105-1–122105-9
Acknowledgements
This work has been performed in the framework of the projects LA 2512/2-1 and WE 2549/24-1. The authors kindly acknowledge the financial support of the Deutsche Forschungsgemeinschaft (DFG). In addition, A. T. acknowledges the Alexander von Humboldt foundation for their funding support.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Initial experimental parameters | Maximum crown parameters | Secondary droplet parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Droplet | Film | D (mm) | U (m/s) | h (mm) | \(\delta\) (–) | We (–) | \(D_{\text{Top}}/D\) (–) | \(H_\mathrm{CR}/D\) (–) | \(D_{\text {Base}}/D\) (–) | \(N_\mathrm{finger,max}\) | \(N_\mathrm{drops,max}\) | \(V_\mathrm{rel}\) (–) | \(\overline{D}_{1,0}\) (mm) | \(\bar{u}_{\text {drops}}\) (m/s) |
Hexadecane | Hyspin | 2.40 | 4.46 | 0.252 | 0.11 | 1343 | 6.38 | 1.92 | 5.06 | 19 | 131 | 2.03 | 0.533 | 1.05 |
Hexadecane | Hyspin | 2.42 | 4.47 | 0.505 | 0.21 | 1363 | 6.08 | 2.68 | 5.49 | 16 | 47 | 1.7 | 0.766 | 1.08 |
Hexadecane | Hyspin | 2.40 | 4.42 | 0.654 | 0.27 | 1315 | 5.86 | 2.71 | 5.96 | 13 | 36 | 1.63 | 0.833 | 1.17 |
Hexadecane | Hyspin | 2.41 | 4.47 | 0.260 | 0.11 | 1356 | 6.48 | 1.93 | 5.11 | 20 | 210 | 2.77 | 0.522 | 1.21 |
Hexadecane | Hyspin | 2.42 | 4.49 | 0.498 | 0.21 | 1369 | 6.09 | 2.65 | 5.25 | 15 | 54 | 2.25 | 0.811 | 1.08 |
Hexadecane | Hyspin | 2.43 | 4.47 | 0.736 | 0.30 | 1361 | 5.9 | 2.92 | 5.93 | 12 | 50 | 2.49 | 0.925 | 1.03 |
Hexadecane | Hyspin | 2.36 | 4.31 | 0.240 | 0.10 | 1236 | 6.5 | 1.91 | 4.97 | 19 | 84 | 1.85 | 0.604 | 0.92 |
Hexadecane | Hyspin | 2.36 | 4.33 | 0.451 | 0.19 | 1245 | 6.08 | 2.6 | 5.26 | 14 | 50 | 1.72 | 0.793 | 0.80 |
Hexadecane | Hyspin | 2.37 | 4.34 | 0.508 | 0.21 | 1253 | 5.97 | 2.74 | 5.26 | 13 | 35 | 1.59 | 0.829 | 0.54 |
Hexadecane | Hyspin | 2.40 | 4.33 | 0.647 | 0.27 | 1267 | 5.81 | 2.76 | 5.86 | 12 | 21 | 1.48 | 1.019 | 0.53 |
Hexadecane | Hyspin | 2.36 | 4.32 | 0.263 | 0.11 | 1236 | 6.48 | 2.03 | 5.09 | 18 | 115 | 1.84 | 0.548 | 1.07 |
Hexadecane | Hyspin | 2.35 | 4.20 | 0.442 | 0.19 | 1166 | 5.94 | 2.29 | 4.96 | 15 | 39 | 1.76 | 0.77 | 0.65 |
Hexadecane | Hyspin | 2.34 | 4.20 | 0.504 | 0.22 | 1158 | 5.84 | 2.39 | 5.1 | 12 | 30 | 1.75 | 0.875 | 0.48 |
Hexadecane | Hyspin | 2.37 | 4.22 | 0.607 | 0.26 | 1191 | 5.76 | 2.53 | 5.31 | 11 | 17 | 1.13 | 1.007 | 0.57 |
Hexadecane | Hyspin | 2.35 | 4.07 | 0.210 | 0.09 | 1094 | 6.6 | 1.77 | 5.14 | 18 | 138 | 2.09 | 0.517 | 1.11 |
Hexadecane | Hyspin | 2.35 | 4.08 | 0.265 | 0.11 | 1099 | 6.38 | 1.96 | 4.97 | 18 | 69 | 1.86 | 0.69 | 0.89 |
Hexadecane | Hyspin | 2.35 | 4.09 | 0.446 | 0.19 | 1104 | 5.96 | 2.39 | 5.18 | 15 | 34 | 1.59 | 0.842 | 0.57 |
Hyspin | Hexadecane | 2.30 | 4.40 | 0.454 | 0.20 | 1363 | 5.41 | 2.98 | 5.5 | 13 | 73 | 2.71 | 0.72 | 1.48 |
Hyspin | Hexadecane | 2.34 | 4.38 | 0.697 | 0.30 | 1375 | 5.34 | 3.22 | 6.07 | 13 | 43 | 2.09 | 0.813 | 1.61 |
Hyspin | Hexadecane | 2.38 | 4.51 | 0.333 | 0.14 | 1483 | 5.79 | 2.88 | 5.27 | 15 | 133 | 3.07 | 0.514 | 1.21 |
Hyspin | Hexadecane | 2.37 | 4.41 | 0.342 | 0.14 | 1413 | 5.68 | 2.81 | 5.23 | 16 | 173 | 2.78 | 0.467 | 1.33 |
Hyspin | Hexadecane | 2.39 | 4.28 | 0.696 | 0.29 | 1341 | 5.21 | 3.2 | 6.05 | 11 | 37 | 2.06 | 0.898 | 1.25 |
Hyspin | Hexadecane | 2.48 | 4.16 | 0.502 | 0.20 | 1314 | 5.3 | 3.04 | 5.57 | 12 | 101 | 2.06 | 0.488 | 1.28 |
Hyspin | Hexadecane | 2.49 | 4.15 | 0.753 | 0.30 | 1313 | 5.43 | 3.18 | 6.22 | 12 | 55 | 1.87 | 0.668 | 1.02 |
Hyspin | Hexadecane | 2.37 | 4.47 | 0.352 | 0.15 | 1453 | 5.74 | 2.78 | 5.22 | 16 | 160 | 3.1 | 0.498 | 1.52 |
Hyspin | Hexadecane | 2.48 | 4.05 | 0.709 | 0.29 | 1242 | 5.3 | 3.07 | 5.89 | 12 | 84 | 1.53 | 0.831 | 1.34 |
Hyspin | Hexadecane | 2.50 | 4.05 | 0.743 | 0.30 | 1256 | 5.39 | 3.08 | 6.05 | 12 | 34 | 1.83 | 0.515 | 1.23 |
Hyspin | Hexadecane | 2.48 | 4.02 | 0.404 | 0.16 | 1229 | 5.61 | 2.78 | 5.23 | 16 | 67 | 2.26 | 0.772 | 1.05 |
Hyspin | Hexadecane | 2.49 | 3.92 | 0.496 | 0.20 | 1173 | 5.51 | 2.78 | 5.41 | 15 | 64 | 1.87 | 0.688 | 1.44 |
Hyspin | Hexadecane | 2.50 | 3.91 | 0.548 | 0.22 | 1171 | 5.42 | 2.87 | 5.59 | 13 | 46 | 2.1 | 0.803 | 0.94 |
Hyspin | Hexadecane | 2.50 | 3.73 | 0.353 | 0.14 | 1065 | 5.59 | 2.63 | 4.92 | 11 | 19 | 0.88 | 0.885 | 0.54 |
Hyspin | Hexadecane | 2.49 | 3.74 | 0.506 | 0.20 | 1071 | 5.58 | 2.59 | 5.31 | 11 | 41 | 1.82 | 0.853 | 1.34 |
Hyspin | Hexadecane | 2.47 | 3.72 | 0.329 | 0.13 | 1048 | 5.6 | 2.38 | 4.88 | 13 | 109 | 2.07 | 0.517 | 1.08 |
Hexadecane | Hexadecane | 2.48 | 4.46 | 0.256 | 0.10 | 1385 | 4.82 | 2.92 | 5.39 | 13 | 171 | 2.190 | 0.315 | 1.81 |
Hexadecane | Hexadecane | 2.40 | 4.43 | 0.458 | 0.19 | 1325 | 3.93 | 3.39 | 5.50 | 15 | 169 | 1.840 | 0.421 | 1.85 |
Hexadecane | Hexadecane | 2.38 | 4.44 | 0.493 | 0.21 | 1313 | 4.13 | 3.42 | 5.71 | 13 | 122 | 1.850 | 0.499 | 1.68 |
Hexadecane | Hexadecane | 2.38 | 4.41 | 0.693 | 0.29 | 1300 | 3.45 | 3.64 | 6.68 | 12 | 187 | 1.120 | 0.346 | 1.51 |
Hexadecane | Hexadecane | 2.47 | 4.43 | 0.749 | 0.30 | 1363 | 3.24 | 3.34 | 5.76 | 10 | 65 | 0.860 | 0.522 | 1.86 |
Hexadecane | Hexadecane | 2.48 | 4.44 | 0.751 | 0.30 | 1374 | 3.33 | 3.40 | 5.90 | 10 | 155 | 1.360 | 0.349 | 1.81 |
Hexadecane | Hexadecane | 2.45 | 4.35 | 0.251 | 0.10 | 1304 | 5.03 | 2.52 | 5.29 | 15 | 204 | 2.640 | 0.450 | 1.76 |
Hexadecane | Hexadecane | 2.41 | 4.25 | 0.510 | 0.21 | 1223 | 4.24 | 3.29 | 5.61 | 11 | 79 | 2.190 | 0.679 | 1.27 |
Hexadecane | Hexadecane | 2.42 | 4.23 | 0.258 | 0.11 | 1212 | 5.06 | 2.72 | 5.27 | 13 | 141 | 1.890 | 0.482 | 1.55 |
Hexadecane | Hexadecane | 2.36 | 4.23 | 0.725 | 0.31 | 1184 | 3.94 | 3.31 | 6.44 | 9 | 46 | 1.260 | 0.599 | 1.12 |
Hexadecane | Hexadecane | 2.38 | 4.11 | 0.246 | 0.10 | 1131 | 5.27 | 2.62 | 5.39 | 14 | 116 | 2.110 | 0.539 | 1.46 |
Hexadecane | Hexadecane | 2.42 | 4.12 | 0.730 | 0.30 | 1152 | 4.16 | 3.20 | 6.04 | 10 | 63 | 1.420 | 0.482 | 1.44 |
Hexadecane | Hexadecane | 2.41 | 3.98 | 0.246 | 0.10 | 1070 | 5.28 | 2.56 | 5.18 | 12 | 50 | 1.910 | 0.727 | 1.08 |
Hexadecane | Hexadecane | 2.42 | 4.00 | 0.475 | 0.20 | 1085 | 4.40 | 3.05 | 5.43 | 10 | 25 | 1.010 | 0.748 | 0.95 |
Hexadecane | Hexadecane | 2.41 | 3.98 | 0.235 | 0.10 | 1075 | 5.49 | 2.55 | 5.33 | 18 | 91 | 2.010 | 0.553 | 1.16 |
Hexadecane | Hsexadecane | 2.44 | 3.83 | 0.470 | 0.19 | 1006 | 5.10 | 2.58 | 5.22 | 13 | 58 | 2.550 | 0.785 | 1.28 |
Hyspin | Hyspin | 2.40 | 4.40 | 0.193 | 0.08 | 1424 | 6.85 | 1.86 | 5.11 | 19 | 42 | 1.010 | 0.681 | – |
Hyspin | Hyspin | 2.37 | 4.41 | 0.237 | 0.10 | 1407 | 7.01 | 2.13 | 5.02 | 15 | 13 | 0.380 | 0.690 | – |
Hyspin | Hyspin | 2.55 | 4.15 | 0.206 | 0.08 | 1345 | 6.90 | 2.03 | 4.99 | 15 | 27 | 0.730 | 0.787 | – |
Hyspin | Hyspin | 2.48 | 4.15 | 0.292 | 0.12 | 1312 | 6.75 | 2.38 | 4.91 | 16 | 17 | 0.470 | 0.731 | – |
Hyspin | Hyspin | 2.49 | 3.99 | 0.186 | 0.07 | 1212 | 6.76 | 1.86 | 5.08 | 14 | 37 | 0.070 | 0.220 | – |
Rights and permissions
About this article
Cite this article
Geppert, A., Terzis, A., Lamanna, G. et al. A benchmark study for the crown-type splashing dynamics of one- and two-component droplet wall–film interactions. Exp Fluids 58, 172 (2017). https://doi.org/10.1007/s00348-017-2447-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-017-2447-2