Skip to main content
SpringerLink
Log in

Effects of an upstream tetrahedron on the circular cylinder–flat plate juncture flow

  • Research Article
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

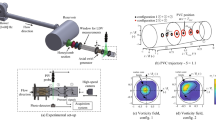
A technique of installing a tetrahedron at the upstream corner of the circular cylinder–flat plate juncture is developed to control the characteristic horseshoe vortices appearing in the natural juncture flow. The Reynolds numbers based on the cylinder diameter are within the range of 500–2900. The flow patterns and time-averaged velocity fields in the vertical symmetry plane and a horizontal plane near the flat plate of the natural and tetrahedron-controlled juncture flows are examined by using the laser-assisted particle flow visualization method and particle image velocimetry in a towing water tank. The flow approaching the circular cylinder–flat plate juncture can induce a characteristic horseshoe vortical flow consisting of a single vortex, dual vortex, or triple vortex. These horseshoe vortices appearing in the natural case may be changed to a characteristic mode of vortical flow, reverse flow, or forward flow when a tetrahedron is installed at the upstream corner of the juncture. The appearance of the vortical flow, reverse flow, or forward flow mode depends on the geometric parameters of normalized axial length, expansion angle, and tilt angle as well as the flow parameter of the Reynolds number. The vortical flow mode appears at small axial length of tetrahedron. The forward flow mode appears at the large axial length of tetrahedron. When the forward flow mode appears, the boundary-layer upstream of the circular cylinder does not separate. Therefore, the horseshoe vortices induced in the natural juncture flow disappear. The data bank consists of the design parameters of axial length, tilt angle, and expansion angle of the tetrahedron, which is provided as a figure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

D :

Diameter of circular cylinder, 50 mm

H :

Length of circular cylinder, 550 mm

L :

Axial length of tetrahedron

Re D :

Reynolds number based on cylinder diameter (=UD/ν)

Re δ :

Reynolds number based on boundary-layer thickness (=Uδ/ν)

U :

Towing velocity

u :

Local axial velocity

x, y, z :

Cartesian coordinates originated at leading edge of juncture

α :

Expansion angle of tetrahedron

β :

Tilt angle of tetrahedron

ρ :

Density of water

δ :

Boundary-layer thickness

δ 1 :

Boundary-layer displacement thickness

δ*:

Inverse of nondimensional boundary-layer displacement thickness (=D/δ 1)

ν :

Kinematic viscosity of water

References

  • Abernethy RB, Benedict RP, Doedell RB (1985) ASME measure uncertainty. J Fluids Eng 107(2):161–164

    Article  Google Scholar 

  • Ahmed F, Rajaratnam N (1998) Flow around bridge piers. J Hydraul Eng 124(3):288–300

    Article  Google Scholar 

  • Akilli H, Rockwell D (2002) Vortex formation from a cylinder in shallow water. Phys Fluids 14(9):2957–2967

    Article  Google Scholar 

  • Baker CJ (1979) The laminar horseshoe vortex. J Fluid Mech 95(2):347–367

    Article  Google Scholar 

  • Baker CJ (1980) The turbulent horseshoe vortex. J Wind Eng Ind Aerodyn 6(1–2):9–23

    Article  Google Scholar 

  • Baker CJ (1985) The position of points of maximum and minimum shear stress upstream of cylinders mounted normal to flat plates. J Wind Eng Ind Aerodyn 18(3):263–274

    Article  Google Scholar 

  • Ballio F, Bettoni C, Frnzetti S (1998) A survey of time-averaged characteristics of laminar and turbulent horseshoe vortices. J Fluids Eng Trans ASME 120(2):233–242

    Article  Google Scholar 

  • Barberis D, Molton P, Malaterre T (1998) Control of 3D turbulent boundary layer separation caused by a wing-body junction. Exp Therm Fluid Sci 16(1):54–62

    Article  Google Scholar 

  • Chou JH, Chao SY (2000) Branching of a horseshoe vortex around surface-mounted rectangular cylinders. Exp Fluids 28(5):394–402

    Article  Google Scholar 

  • Dargahi B (1990) Controlling mechanism of local scouring. J Hydraul Eng 116(10):1197–1214

    Article  Google Scholar 

  • Devenport WJ, Simpson RL (1990) Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction. J Fluid Mech 210:23–25

    Article  Google Scholar 

  • Devenport WJ, Agarwal NK, Dewitz MB, Simpson RL, Poddar K (1990) Effects of a fillet on the flow past a wing-body junction. AIAA J 28(12):2017–2024

    Article  Google Scholar 

  • Devenport WJ, Simpson RL, Dewita MB, Agarwal NK (1992) Effects of a leading-edge fillet on the flow past an appendage-body junction. AIAA J 30(9):2177–2183

    Article  Google Scholar 

  • El Hassan M, Bourgeois J, Martinuzzi R (2015) Boundary layer effect on the vortex shedding of wall-mounted rectangular cylinder. Exp Fluids 56(2):33

    Article  Google Scholar 

  • Flagan RC, Seinfeld JH (1988) Fundamentals of air pollution engineering. Prentice-Hall, Englewood Cliffs, pp 290–357

    Google Scholar 

  • Gupta AK (1987) Hydrodynamic modification of the horseshoe vortex at a vertical pier junction with ground. Phys Fluids 30(4):1213–1215

    Article  Google Scholar 

  • Hosseini Z, Bourgeois JA, Martinuzzi RJ (2013) Large-scale structures in dipole and quadrupole wakes of a wall-mounted finite rectangular cylinder. Exp Fluids 54(9):1595

    Article  Google Scholar 

  • Huang RF, Hsu CM, Lin WC (2014) Flow characteristics around juncture of a circular cylinder mounted normal to a flat plate. Exp Therm Fluid Sci 55(1):187–199

    Article  Google Scholar 

  • Hunt JCR, Abell CJ, Peterka JA, Woo H (1978) Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J Fluid Mech 86(1):179–200

    Article  Google Scholar 

  • Kairouz KA, Rahai HR (2005) Turbulent junction flow with an upstream ribbed surface. Int J Heat Fluid Flow 26(3):771–779

    Article  Google Scholar 

  • Keane RD, Adrian RJ (1992) Theory of cross-correlation analysis of PIV images. Appl Sci Res 49(3):191–215

    Article  Google Scholar 

  • Kirkil G, Constantinescu G (2012) A numerical study of the laminar necklace vortex system and its effect on the wake for a circular cylinder. Phys Fluids 24(7):073622

    Article  Google Scholar 

  • Martinuzzi R, Tropea C (1993) The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. J Fluid Eng 115(1):85–92

    Article  Google Scholar 

  • Melville BW (1997) Pier and abutment scour: integrated approach. J Hydraul Eng 123(1):125–136

    Article  MathSciNet  Google Scholar 

  • Melville BW, Chiew Y-M (1999) Time scale for local scour at bridge piers. J Hydraul Eng 125(1):59–65

    Article  Google Scholar 

  • Ölçmen SM, Simpson RL (1995) An experimental study of a three-dimensional pressure-driven turbulent boundary layer. J Fluid Mech 290:225–262

    Article  Google Scholar 

  • Pattenden RJ, Turnock SR, Zhang X (2005) Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp Fluids 39(1):10–21

    Article  Google Scholar 

  • Perry AE, Steiner TR (1987) Large-scale structures in turbulent wakes behind bluff bodies. Part 1. Vortex formation. J Fluid Mech 174:223–270

    Article  Google Scholar 

  • Philips DB, Cimbala JM, Treaster AL (1992) Suppression of the wing-body junction vortex by body surface suction. J Aircr 29(10):118–122

    Article  Google Scholar 

  • Porteous R, Moreau DJ, Doolan CJ (2014) A review of flow-induced noise from finite wall-mounted cylinders. J Fluids Struct 51:240–254

    Article  Google Scholar 

  • Rodríguez y Domínguez M, Romero-Méndez R, Ramos-Paláu M, Pérez-Gutiérrez FG (2006) The laminar horseshoe vortex upstream of a short-cylinder confined in a channel formed by a pair of parallel plates. Journal of Visualization 9(3):309–318

    Article  Google Scholar 

  • Sahin B, Ozturk NA (2009) Behaviour of flow at the junction of cylinder and base plate in deep water. Measurement 42(2):225–240

    Article  Google Scholar 

  • Sahin B, Ozturk NA, Akilli H (2007) Horseshoe vortex system in the vicinity of the vertical cylinder mounted on a flat plate. Flow Meas Instrum 18(1):57–68

    Article  Google Scholar 

  • Seal CV, Smith CR (1999a) Visualization of a mechanism for three-dimensional interaction and near-wall eruption. J Fluid Mech 394:193–203

    Article  Google Scholar 

  • Seal CV, Smith CR (1999b) The control of turbulent end-wall boundary layers using surface suction. Exp Fluids 27(2):484–496

    Article  Google Scholar 

  • Seal CV, Smith CR, Akin O, Rockwell D (1995) Quantitative characteristics of a laminar, unsteady necklace vortex system at a rectangular block-flat plate juncture. J Fluid Mech 286:117–135

    Article  Google Scholar 

  • Simpson RL (2001) Junction flows. Annu Rev Fluid Mech 33:415–443

    Article  Google Scholar 

  • Smith FT, Gajjar J (1984) Flow past wing-body junctions. J Fluid Mech 144:191–215

    Article  MATH  Google Scholar 

  • Sumner D, Heseltine JL (2008) Tip vortex structure for a circular cylinder with a free end. J Wind Eng Ind Aerodyn 96(6–7):1185–1196

    Article  Google Scholar 

  • Sumner D, Heseltine JL, Dansereau OJP (2004) Wake structure of a finite circular cylinder of small aspect ratio. Exp Fluids 37(5):720–730

    Article  Google Scholar 

  • Tennekes H, Lumley JL (1983) A first course in turbulence. MIT Press, Cambridge

    Google Scholar 

  • Wang JM, Bi WT, Wei QD (2009) Effects of an upstream inclined rod on the circular cylinder-flat plate junction flow. Exp Fluids 46(6):1093–1104

    Article  Google Scholar 

  • Wei QD, Wang JM, Chen G, Lu ZB, Bi WT (2008) Modification of junction flows by altering the section shapes of the cylinders. J Vis 11(2):115–124

    Article  Google Scholar 

  • Westerweel J (2000) Theoretical analysis of the measurement precision in particle image velocimetry. Exp Fluids 29(1):S3–S12

    Article  Google Scholar 

  • White FM (1991) Viscous Fluid Flow, 2nd edn. McGraw-Hill, New York, pp 233–240

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Taiwan University of Science and Technology, Taipei, 10672, Taiwan, ROC

    R. F. Huang & C. Chen

  2. Graduate Institute of Applied Science and Technology, National Taiwan University of Science and Technology, Taipei, 10672, Taiwan, ROC

    C. M. Hsu

Authors
  1. R. F. Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. M. Hsu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. F. Huang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, R.F., Hsu, C.M. & Chen, C. Effects of an upstream tetrahedron on the circular cylinder–flat plate juncture flow. Exp Fluids 56, 146 (2015). https://doi.org/10.1007/s00348-015-2020-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00348-015-2020-9

Keywords

Search

Navigation