Abstract
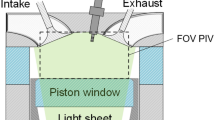
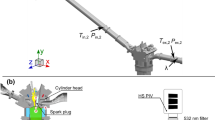
We define and illustrate a cluster-based analysis of cycle-to-cycle variations (CCV). The methodology is applied to engine flow but can clearly be valuable for any periodically driven fluid flow at large Reynolds numbers. High-speed particle image velocimetry data acquired during the compression stroke for 161 consecutive engine cycles are used. Clustering is applied to the velocity fields normalised by their kinetic energy. From a phase-averaged analysis of the statistics of cluster content and inter-cluster transitions, we show that CCV can be associated with different sets of trajectories during the second half of the compression phase. Conditional statistics are computed for flow data of each cluster. In particular, we identify a particular subset associated with a loss of large-scale coherence, a very low kinetic energy of the mean flow and a higher fluctuating kinetic energy. This is interpreted as a good indicator of the breakdown of the large-scale coherent tumbling motion. For this particular subset, the cluster analysis confirms the idea of a gradual destabilisation of the in-cylinder flow during the final phase of the compression. Moreover, inter-cycle statistics show that the flow states near TDC and in the measurement zone are statistically independent for consecutive engine cycles. It is important to point out that this approach is generally applicable to very large sets of data, e.g. generated by PIV or LES, and independent of the considered type of information (velocity, concentration, etc.).








Similar content being viewed by others
References
Arcoumanis C, Hu Z, Whitelaw JH (1990) Tumbling motion: a mechanism for turbulence enhancement in spark-ignition engines. SAE paper 900060
Bishop CM (2006) Pattern recognition and machine learning (information science and statistics). Springer, New York
Bizon K, Continillo G, Mancaruso E, Merola SS, Vaglieco BM (2010) POD-based analysis of combustion images in optically accessible engines. Comb Flame 157:632–640
Borée J, Miles P (2014) In-cylinder flow. In: Crolla D, Foster DE, Kobayashi T, Vaughan N (eds) Encyclopedia of automotive engineering. Wiley, Chichester
Borg I, Groenen PJ (2005) Modern multidimensional scaling: theory and applications. Springer, Berlin
Chen H, Reuss DL, Sick V (2012) On the use and interpretation of proper orthogonal decomposition of in-cylinder flows. Meas Sci Technol 23(8):1–14
Chen H, Hung DLS, Xu M, Zhuang H, Yang J (2014) Proper Orthogonal decomposition analysis of fuel spray structure variation in a spark-ignition direct-injection optical engine. Exp Fluids 55:1703–1715
Cosadia I, Borée J, Charnay G, Dumont P (2006) Cyclic variations of the swirling flow in a Diesel transparent engine. Exp Fluids 41(1):115–134
Du Q, Gunzburger MD (2003) Centroidal Voronoi tessellation based proper orthogonal decomposition analysis. In: Desch W, Kappel F, Kunisch K (eds) Control and estimation of distributed parameter systems. Birkhäuser, Basel, pp 137–150
Fogleman MA (2005) Low dimensionnal models of internal combustion engine flows using the proper orthogonal decomposition, PhD Thesis, Cornell University
Fogleman M, Lumley JL, Rempfer D, Haworth D (2004) Application of the proper orthogonal decomposition to datasets of internal combustion engine flows. J Turbul 5:1–18
Gosman AD (1986) Flow processes in cylinders. Thermodynamics and gas dynamics of internal combustion engines, vol 2. Oxford University Press, Oxford, pp 616–772
Hasse C, Sohm V, Durst B (2010) Numerical investigation of cyclic variations in gasoline engines using a hybrid URANS/LES modeling approach. Comput Fluids 39:25–48
Heywood JB (1988) Internal combustion engines fundamentals. McGRAW Hill Company, New York
Hill PG, Zhang D (1994) The effects of swirl and tumble on combustion in spark-ignition engines. Prog Energy Combust Sci 20:373–429
Holmes P, Lumley JL, Berkooz G, Rowley CW (2012) Turbulence, coherent structures, dynamical systems and symmetry, 2nd edn. Cambridge University Press, Cambridge
Kaiser E, Noack BR, Cordier L, Spohn A, Segond M, Abel M, Daviller G, Östh J, Krajnovic S, Niven RK (2014) Cluster-based reduced-order modelling of a mixing layer. J Fluid Mech 754:365–414
Kapitsa L, Imberdis O, Bensler HP, Willand J, Thévenin D (2010) An experimental analysis of the turbulent structures generated by the intake port of a DISI-engine. Exp Fluids 48:265–280
Keromnes A, Dujol C, Guibert P (2010) Aerodynamic control inside an internal combustion engine. Meas Sci Technol 21:125–404
Liu K, Haworth D (2011) Development and assessment of POD for analysis of turbulent flow in piston engines. SAE Technical paper 2011-01-0830
Lloyd SP (1957) “Least square quantization in PCM”. Bell Telephone Laboratories Paper. Published: Lloyd., S. P. (1982). “Least squares quantization in PCM”. IEEE Trans Inf Theory 28(2):129–137. doi:10.1109/TIT.1982.1056489
Lumley JL (1967) The structure of inhomogeneous turbulence. In: Yaglom AM, Tatarski VI (eds) Atmospheric turbulence and wave propagation. Nauka, Moscow, pp 166–178
Lumley JL (1999) Engines. An introduction. Cambridge University Press, Cambridge
Lundgren TS, Mansour NN (1996) Transition to turbulence in an elliptic vortex. J Fluid Mech 307:43–62
MacQueen J (1967) Some methods for classification and analysis of multivariate observations. In: Proceedings of the fifth Berkeley symposium on mathematical statistics and probability 1:281–297
Schneider TM, Eckhardt B, Vollmer J (2007) Statistical analysis of coherent structures in transitional pipe flow. Phys Rev E 75(6):066313
Voisine M, Thomas L, Borée J, Rey P (2011) Spatio-temporal structure and cycle-to-cycle variations of an in-cylinder tumbling flow. Exp Fluids 50(5):1393–1407
Acknowledgments
The PhD grant of Y. CAO is financed by Renault. The work is partially funded by the ANR Chair of Excellence TUCOROM. E. Kaiser acknowledges additional funding from region Poitou–Charentes, France, ANR Project “SePaCoDe” (Étude de la Physique du Décollement et Réalisation de son Contrôle) and NSF PIRE Grant OISE-0968313.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cao, Y., Kaiser, E., Borée, J. et al. Cluster-based analysis of cycle-to-cycle variations: application to internal combustion engines. Exp Fluids 55, 1837 (2014). https://doi.org/10.1007/s00348-014-1837-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-014-1837-y