1 Introduction

Although our knowledge of the mechanism of how vegetation dissipates wave energy and contributes to shoreline protection by damping waves continues to increase, large areas of offshore vegetation and wetlands continue to be degraded and destroyed each year (USEPA 2007), and vegetation benefits, which also include aesthetics, habitat, and biodiversity, are lost with their removal. Vegetation has been shown to effectively attenuate flow (Fonseca et al. 1982; Peterson et al. 2004) and wave energy (Dean 1978; Fonseca and Cahalan 1992; Kobayashi et al. 1993; Mendez et al. 1999; Möller et al. 1999; Dean and Bender 2006; Augustin et al. 2009). Several models for predicting wave dissipation through vegetation have been proposed based on the conservation of energy (Dalrymple et al. 1984; Mendez and Losada 2004) and conservation of momentum (Kobayashi et al. 1993) for linear waves, and these have subsequently been expanded and new models proposed (Dubi and Torum 1995; Mendez et al. 1999; Chen and Zhao 2012). Additional models investigating wave attenuation under the combination of wave flow and current flow (Ota et al. 2005; Li and Yan 2007) have also been proposed.

As these models have grown in complexity, they are better able to address conditions found in the field, but to predict these conditions they require input parameters that are species-specific. Bulk drag characterization from the wave height decay through a field of plant elements in a test flume or site is often used as a standard of practice (USACE 2006). The bulk drag characterization requires the establishment of an obstruction field. This method can be cumbersome and the results cannot be translated over to other species easily (Bouma et al. 2010), and needs to be performed on each species or plant morphology (USACE 2006). Even within a single species, the seasonal changes in plant foliage influence the bulk canopy drag (Schoneboom and Aberle 2009), so testing at several different stages of growth is needed to fully characterize some species (Paul and Amos 2011).

We have instrumented a single plant element instead of evaluating the flow conditions before and after the obstruction network, eliminating the time and expense needed for establishing an entire vegetation field. We feel this is advantageous as experiments can be run more efficiently on a larger number of species. This is similar to an approach used by Wunder et al. (2009) and Schoneboom and Aberle (2009). While Wunder et al. (2009) used a frame to mount elements and transmit forces to a load cell and Schoneboom and Aberle (2009) used a load cell mounted below the flume, we used a torque sensor mounted below the flume to simplify these arrangements further and provide a high-frequency temporal response. While torque sensors have been used in previous studies (Flocard and Finnigan 2009; Pasternack et al. 2007), they have not previously been mounted with vegetation or vegetation surrogates.

The lack of information on species limits the usefulness of the models developed, and generalizations of plant behavior have not proved to be robust enough for practice (Mendez and Losada 2004). While some species, such as Cabomba caroliana, Nympheae rubra, and Eichinodorus grandifloru (Penning et al. 2009), Laminaria hyperborea (Dubi and Torum 1995; Mork 1996), Macrocystis pyrifera (Elwany et al. 1995; Elwany and Flick 1996), Posidonia oceanica (Gacia and Duarte 2001; Stratigaki et al. 2009), Spartina alterniflora (Möller et al. 1996, 1999), and Zostera marina (Fonseca and Cahalan 1992; Ifuku and Hayashi 1998), have been characterized for energy dissipation parameters, many more species have no information available. Establishing the relationships of drag to the Reynolds number (Re), using the orbital velocity and vegetation diameter as the characteristic length, and Keulegan–Carpenter number (KC), using the orbital velocity and vegetation diameter as the characteristic length, have also been attempted with some success (Mendez and Losada 2004; Augustin et al. 2009), but there has not been strong evidence which one of these non-dimensional parameters is better suited to represent drag for plants (USACE 2006). Sarpaka and Isaacson (1981) extensively look at the interrelation of drag and momentum of obstructions in waves to Re and KC, along with other non-dimensional parameters, but do not unite these parameters in one relation. Use of a non-dimensional drag coefficient is advantageous as it is independent of plant area, which may change seasonally, but is dependent on the morphology and hydrodynamics. For Thalassia testudinum (Bradley and Houser 2009), Zostera noltti (Paul and Amos 2011), and artificial kelp (Kobayashi et al. 1993; Mendez et al. 1999), exponential functions of Reynolds number were determined for the estimation of drag coefficients with reasonable accuracy.

Procedures have been developed to translate individual obstruction drag elements into a canopy drag (Dalrymple et al. 1984; Kobayashi et al. 1993; Mendez et al. 1999). These methods based on the fundamental principles of energy and momentum conservation and superposition have been used to reasonably model canopies, but the drag parameters for the bulk system are often modified from the drag parameters associated with individual elements.

Many previous studies have incorporated rigid elements to simulate vegetation fields in directional fluid flow (Nepf 1999; Poggi et al. 2004; Nezu and Sanjou 2008), directional atmospheric flow (Finnigan 2000), and in wave fluid flow (Dalrymple et al. 1984), but there have been fewer studies that have incorporated flexible elements into the experimental design in either direct flow (Ghisalberti and Nepf 2006; Wunder et al. 2009) or in wave conditions (Augustin et al. 2009). Some research has looked at simpler properties such as wet biomass (Penning et al. 2009) for defining the parameters of vegetation, but a more efficient characterization method is still needed.

Studies focusing on the characterization of turbulence through laser and Doppler techniques (Finnigan 2000; Poggi et al. 2004; Nezu and Sanjou 2008) have provided insight into the wake effects and eddy structures that develop in canopies. While this is fundamental to deeper understanding of the interactions within the canopy, there is also a need for breaking the complexities down into simpler components such as the basic characterization of drag force differences occurring due to the flexibility of vegetation.

Our goal is to characterize and predict vegetation drag forces by collecting data on a single vegetation element in a flume, as opposed to establishing a full network of vegetation and monitoring wave decay affects. We have used the torque sensor instrumentation arrangement to measure the forces on artificial vegetation under wave conditions. We have used both rigid and flexible artificial vegetation and also with a single element and with a single element located within a field of artificial vegetation, although the methodology is applicable for a great variety of vegetation morphologies. The experimental setup can be used to study directional flow and wave conditions; however, wave conditions are of greater importance in shoreline protection and are the focus of the data in this paper.

While use of a torque sensor cannot separate force components of form drag, skin friction drag, and others, it does provide a total drag reaction occurring at the base of the artificial vegetation, which is suitable for this study. Wake interactions are not monitored directly with this instrument, but can be inferred by comparing reactions when upstream artificial vegetation is present or not. Additionally, by using fully emergent artificial vegetation, we have limited the scope of this work to consider flow within the vegetation canopy.

2 Background

The form drag force on artificial vegetation can be estimated, assuming an unsteady, non-uniform flow of a viscous fluid and neglecting inertial forces of the vegetation, and can also be interpreted as a torque at the base of the vegetation, as seen in Eq. (1),

$$F_{d} = \mathop \int \limits_{o}^{d} \frac{1}{2}C_{D} \rho w u^{2} {\text{d}}z = \mathop \int \limits_{o}^{d} \frac{1}{z}\left( {\frac{{{\text{d}}T_{d} }}{{{\text{d}}l}}} \right){\text{d}}z$$
(1)

where F D  = drag force, u = flow velocity, w = projected vegetation width, C D  = drag coefficient of vegetation, ρ = fluid density, T d  = the torque on the vegetation at z, l = moment arm for vegetation at z, d = flow depth, T is the total torque, and z = vertical position up from the bed. For the limit as z approaches the bottom of the channel, we assume that (T d /l) approaches zero by linear wave theory.

The velocity profile can be determined using linear wave theory and the measured wave height (Sorensen 2006) will be used with determined moment arm estimates to convert the torque data into resultant forces.

Using a constant, representative drag coefficient, Eq. (1) can be simplified using Δz = d/n to create Eq. (2),

$$F_{d} = \frac{1}{2}C_{D} \rho \Delta z\mathop \sum \limits_{i = 1}^{n} w_{i} u_{i}^{2} = \frac{T}{l}$$
(2)

where n is the number of vertical grid points. The spatially averaged drag coefficient for a measured total torque acting on the vegetation over a known mean water depth can be determined using Eq. (3).

$$C_{D} = \frac{{\left( \frac{T}{l} \right)}}{{\left( \frac{1}{2} \right)\rho \Delta z\mathop \sum \nolimits_{i = 1}^{n} w_{i} u_{i}^{2} }}$$
(3)

The moment arm was estimated using the sum of the wave amplitude and mean water depth, and the velocity was determined from the calculated orbital velocity within the wave. The drag force calculation can be further simplified by assuming the mean water depth as the moment arm as in Eq. (4), where T is the total sum of torque on the vegetation.

$$\tilde{F}_{d} = T/\tilde{l}$$
(4)

Equation (4) is a useful simplification when the torque and drag forces vary with time as they do in wave conditions. Under wave conditions, the torque response will vary with each wave period and while translation of this signal into a single representative value can be done using an RMS average, it can also be translated into a single value by integrating over time. Combining Eqs. (1) and (4) and using the integration limits of time gives Eq. (5), which is an expression for the time-averaged drag coefficient.

$$\tilde{C}_{D} = \frac{{\mathop \int \nolimits_{o}^{t} \frac{T}{{\tilde{l}}} {\text{d}}t}}{{\mathop \int \nolimits_{o}^{t} \frac{1}{2}\rho A u^{2} {\text{d}}t}}$$
(5)

where A is the vegetation projected area and t is the time in data series. A correction for the simplified moment arm based on the orbital velocity profile can be applied to Eq. (5), to have a more accurate value as shown in Eq. (6), where β is the reduction in the moment arm estimated using the resultant depth-averaged velocity equivalent to the calculated orbital velocity profile using the wave period determined from the spectral density plot.

$$C_{D} = \tilde{C}_{D} * \beta$$
(6)

where C D is the drag coefficient, \(\tilde{C}_{D}\) is the time-averaged drag coefficient, and β is the reduction factor based on wave period.

3 Methods

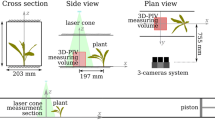
An indoor experimental flume in the Biosystems and Agricultural Engineering Building on the St. Paul campus of the University of Minnesota was used in this study was retrofitted to include a submersible torque sensor below the flume floor, to which artificial vegetation could be attached and subjected to either directional flow or wave conditions. The submersible torque sensor allowed for direct measurement of the torque on the vegetation from the flow, and back calculation of the drag forces occurring on the vegetation.

A schematic of the experimental flume is shown in Fig. 1. The flume has a total length of 7.25 m, an interior flow width of 0.38 m, and total depth of 0.38 m. This flume has an additional wet well extending 0.2 m below the flume over a 2.1 m test section. This allows for elements to be placed below the flume floor, such as submersible sensors. The flume is primarily constructed out of PVC with steel reinforcement. The flume bottom is lined with 1 mm diameter sand adhered to metal sheets. The slope of the flume can be adjusted using screw jack supports.

Fig. 1
figure 1

Flume schematic, vegetation layout, and photograph of test section

Full size image

When operated for wave simulation, an artificial beach is placed in the last 1 m of the flume. A hinged paddle is used to generate waves using a 12-V DC motor stepped down to a paddle arm through a belt and pulleys.

The flume wet well allows for a FUTEK TFF425 submersible torque sensor to be mounted below the flume, with a single vegetation element attached to the sensor passing up through the floor of the flume into the flow, 0.62 m behind the start of the obstruction canopy when used. The torque sensor has a 0.047 N m maximum capacity, suitable to measure small loadings such as those occurring from a single small diameter vegetation stem. The FUTEK SensIT Test and Measurement version 2.1.4 software and FUTEK USB210 interface were used to read and calibrate the data from the sensor. This model of torque sensor has a flange end, and a PVC plate was mounted onto the flange with springs, to allow obstruction elements and vegetation to be mounted to the sensor through compression.

Water surfaces are measured using RBR WG-55 capacitance level sensors. One WG-55 sensor is placed adjacent to the vegetation to measure the wave conditions near the vegetation torque data. A second WG-55 sensor is placed 1.85 m upstream of the vegetation element to characterize the wave conditions prior to any vegetation. The WG-55 sensor data were collected using a DATAQ DI-149 voltage data logger. A submersible digital video camera placed in the wet well was also used to film the vegetation through the clear flume wall marked with grid lines at 5 mm spacing for data verification. The statistical software program R (RDCT 2011) was used for spectral signal analysis using packages of stats (Venables and Ripley 2002), car (Fox and Weisberg 2011), and pastecs (Ibanez et al. 2013).

Three different artificial vegetation stems covering a range of flexibilities were used in these experiments, made of aluminum, polyurethane foam, and a thin-walled polyethylene straw. These will be referred to as aluminum, foam, and straw vegetation for simplification. We attempted to use artificial vegetation with similar size, shape, and surface texture. The vegetation diameters and other physical properties are reported in Table 1.

Table 1 Artificial vegetation physical properties
Full size table

Table 1 lists the artificial vegetation and their Young’s modulus, or moduli of elasticity as determined by loading the vegetation as a cantilevered beam. The moduli were determined as if the element was a solid homogeneous cylindrical mass, which is not the case for all artificial vegetation tested or for live vegetation, but this technique allows for a comparison of flexibility.

Table 1 also includes the artificial vegetation-specific gravity. While specific gravity is a property of the material, some of the artificial vegetation has voids filled with air or water, depending on saturation. An effective specific gravity can be calculated for the composite artificial vegetation assuming the voids are filled with water during the experiment. The two m* properties in Table 1 are used to quantify the damping due to the mass of an oscillating object. Gabbi and Benaroya (2005) represented this damping using m* defined as the mass of the obstruction divided by the fluid density and by the square of the vegetation diameter. Due to the saturated void space, an m* effective can also be calculated assuming all the open voids are saturated with water.

The experimental setup can be used for the measurement of the natural frequency of the vegetation tested. When vegetation is located in the torque sensor, it is possible to apply a single temporary force and monitor the response after the force is released. The torque signal decay (Fig. 2) can be used to measure the natural frequency (f o ) and the damping coefficient (α), as reported in Table 1. The natural frequency is the inverse of the difference between torque peak values. The damping ratio is the natural log of the ratio of peak torque for two consecutive cycles divided by 2π. Due to the low mass of the foam vegetation, the frequency and slow decay response shown for the foam vegetation is mostly generated by the mass of the torque sensor itself. The natural frequency of the torque sensor without mounted vegetation is the same as the frequency response with the foam vegetation. The spatial distribution of vegetation mass along the vegetation length is believed to cause the differences in the rate of signal decay or damping seen in the straw and aluminum vegetation.

Fig. 2
figure 2

Natural vibration response of the aluminum, foam, and straw artificial vegetation in the experimental setup

Full size image

Experiments were performed with networks of artificial vegetation arranged upstream from the test element. The networks included rows of additional vegetation downstream of the test vegetation stem. These artificial vegetation canopies were mounted using threaded studs in panels on the floor of the flume. The canopy vegetation was arranged in a staggered pattern at different densities corresponding to flow vegetation fractional volumes of flow domain ranging from 0.003 to 0.025 (Table 2) where a fractional volume of the flow domain is defined as the ratio of vegetation diameter squared to mean vegetation spacing distance squared (Nepf 1999).

Table 2 Artificial vegetation network (canopy) spacing
Full size table

Five different wave conditions were generated for each vegetation arrangement and were varied by altering the wave period through the frequency of the wave paddle motion. Wave periods generated ranged from 0.7 to 1.1 s (Table 3), and the water depth in the flume was 0.22 ± 0.02 m, as limited by the flume and wave generator construction. The vegetation size and wave heights correspond to full scale for some shallow inland lakes with emergent vegetation.

Table 3 Wave parameters
Full size table

4 Results and discussion

The instrumentation system is able to provide quick useful analysis of drag forces from a variety of obstruction types in wave conditions as tested. The water surface displacement can be coupled with our torque response to provide insight into drag forces. The output values from the torque sensor did not require any additional manipulation or adjustment with the experimental setup, as would be necessary using load cells with mounting arms (Wunder et al. 2009). The technique also allowed for the evaluation of several types of vegetation quickly without the need to set up entire vegetation fields.

The torque response contained in it dominant frequencies that were directly related to the major driving wave frequency of the experiment (Figs. 3, 4, 5). In addition to the dominant frequency related to the wave period, the torque response had additional frequencies for different artificial vegetation. The number of these frequencies varied with the type of artificial vegetation. The less flexible aluminum vegetation had fewer frequencies (Fig. 3) compared to the straw (Fig. 4) and foam (Fig. 5). Foam had the most additional frequencies, which the authors speculate is due to the greater flexibility and subsequent greater motion.

Fig. 3
figure 3

Two seconds of aluminum artificial vegetation torque response in waves. The wave height at the instrumented vegetation is on the left axis, and the vegetation torque is shown on the secondary axis

Full size image
Fig. 4
figure 4

Two seconds of straw artificial vegetation torque response in waves. The wave height at the instrumented vegetation in on the left axis, and the vegetation torque is shown on the secondary axis

Full size image
Fig. 5
figure 5

Two seconds of foam artificial vegetation torque response in waves. The wave height at the instrumented vegetation in on the left axis, and the vegetation torque is shown on the secondary axis

Full size image

The magnitude of the torque response is also stronger in the less flexible aluminum, on the order of 0.02 N m peak values, compared to the more flexible straw element, on the order of 0.01 N m peak values, or the most flexible foam vegetation having peak torque values of 0.002 N m peak values. The more rigid vegetation will either transfer more forces to the base where they are observed by the torque sensor, while the more flexible vegetation will not transfer all of the force to the base and distribute energy by greater motion, or receive more drag force than the flexible vegetation due to their reduced deformation compared to the flexible vegetation.

Since the flow depths are approximately equal in Figs. 3, 4, and 5, drag forces are directly related to the magnitude of the torque readings for these tests. More flexible vegetation in our tests resulted in smaller drag forces and drag coefficients. This outcome is similar to that obtained by Mullarney and Henderson (2010) for their investigations of Schoenoplectus americanus. They found that wave dissipation, which can be estimated from the drag (Dalrymple et al. 1984), for flexible stems was only 30 % of that predicted for rigid stems. This effect was frequency-dependent with a maximum reduction around 1 Hz. However, the trends in Figs. 3, 4, and 5 are different than those obtained by Wunder et al. (2009). Flexibility increased drag forces in their study of what was referred to as a willow branch. The topology, natural frequency, and damping coefficient of the willow branch might account for the different response.

A fast Fourier transform was used to develop spectral density plots of the torque response using Program R (RDCT 2011) and associated packages. Torque values and wave height values are also correlated with time (Devore 2001) using the same software. Results are summarized in Figs. 6, 7, and 8 and are discussed below. The spectral density is highly periodic, and as expected, the largest spectral density occurs at a frequency value that correlates with the driving water wave frequency, but additional frequencies also have large spectral density values.

Fig. 6
figure 6

Comparison of two torque correlation and torque spectral density plots of the aluminum artificial vegetation with a natural frequency of 4.46 Hz. a and c are from the same experiment that had a vegetation drag force of 0.009879N, wave height of 0.022 m, wave period of 1.03 s, and mean water depth of 0.218 m. b and d are from the same experiment that had a vegetation drag force of 0.02361 N, wave height of 0.022 m, wave period of 0.91 s, and mean water depth of 0.23 m

Full size image
Fig. 7
figure 7

Comparison of two torque correlation and torque spectral density plots of the straw artificial vegetation with a natural frequency of 6.49 Hz. a and c are from the same experiment that had a vegetation drag force of 0.0111 N, wave height of 0.023 m, wave period of 0.96 s, and mean water depth of 0.206 m. b and d are from the same experiment that had a vegetation drag force of 0.0212 N, wave height of 0.014 m, wave period of 0.91 s, and mean water depth of 0.208 m

Full size image
Fig. 8
figure 8

Comparison of two torque correlation and torque spectral density plots of the foam artificial vegetation with a natural frequency of 10 Hz. a and c are from the same experiment that had a vegetation drag force of 0.01883 N, wave height of 0.0146 m, wave period of 0.9 s, and mean water depth of 0.198 m. Figure 8b, d are from the same experiment that had a vegetation drag force of 0.009694 N, wave height of 0.0191 m, wave period of 1.04 s, and mean water depth of 0.24 m

Full size image

Figure 6a combines the torque and wave data into a single correlation plot and while Fig. 6c shows the spectral density results, an experiment with aluminum vegetation. Figure 6b, d show a similar correlation plot and spectral density information for another experiment with aluminum vegetation under slightly different wave frequencies. The vegetation Re is nearly the same for the two runs, the wave heights are both 0.022 m, the same dense network density is used, the mean water depth is 0.218 and 0.23, but the wave period is 1.03 s for Fig. 6a, c and 0.87 s for Fig. 6b, d. We calculated Re using the maximum orbital velocity in the wave and the vegetation diameter for the length scale. The drag force corresponding to Fig. 6c is approximately 2.4 times larger than that corresponding to Fig. 6d. Insight into this difference can be obtained by considering the power spectral densities for the two runs. The power spectral density is proportional to the modulus squared of the Fourier amplitude at each frequency and is the power distributed over the observed frequency range. To simplify interpretation, the power spectral density results are presented in Fig. 6c, d as a percentage of total spectral density with respect to a normalized frequency, defined as the torque frequency divided by the dominant fluid wave frequency. The influence of the driving fluid wave frequency in response to the torque may be seen in Fig. 6c, d where the strongest signal matches the wave frequency. However, Fig. 6c has a greater number of subsequent frequencies, which appear to be resonant frequencies, in the torque response compared to Fig. 6d.

Figures 7 and 8 for the straw and foam vegetation show similar response as seen in Fig. 6. The flow conditions for Fig. 7 have Re of 725 and 614, wave heights of 0.022 and 0.013 m, periods of 0.96 and 0.91 s, and depths of 0.206 and 0.208 m for the Fig. 7a, c paired plots and Fig. 7b, d paired plots, respectively. For the straw, the drag forces are again smaller for the conditions of Fig. 7a than those of Fig. 7b as they were with the aluminum vegetation. However, for the foam vegetation, we do not have two runs that can be compared having similar character in the spectral density. The flow conditions for Fig. 8 have Re of 1,020 and 932, wave heights of 0.014 and 0.017 m, periods of 0.9 and 1.04 s, and depths of 0.198 and 0.24 m for the Fig. 8a, c paired plots and Fig. 8b, d paired plots, respectively. There was not a reduction in drag force to the strength of the spectral density at the secondary frequency (Fig. 8) so little can be concluded from this. The secondary frequencies in the foam vegetation did correspond to a 10-Hz signal, which is possibly due to the torque sensor mass that was not damped by the vegetation mass.

The largest spectral density in the torque frequencies matches the wave frequency as forced by the wave generator, as seen in Figs. 6, 7, and 8 where the largest signal is at a frequency ratio of 1. Subsequent frequency values are harmonic values of the torque frequency. We have compared the amount of spectral density occurring at this wave frequency to the total spectral density plot in order to index this phenomenon. Figure 6d has 85 % of the energy density concentrated into the fundamental frequency, and Fig. 6c has 60 % of the energy density concentrated into the fundamental frequency. A lower percentage of the energy density occurring at the driving wave frequency suggests there are more competing significant frequencies in the signal. Figure 9a shows the drag force estimated from torque compared to the percentage of spectral energy density occurring in the driving wave fundamental frequency for the dense vegetation network. Figure 9b shows data for the intermediate density networks, and Fig. 9c shows only data collected using the thinnest network of vegetation having a flow obstruction fractional volume of 0.002 to 0.007 upstream of the test vegetation stem. Greater spectral density occurring in a fundamental frequency, which the authors attribute to the evidence of synchronization where frequencies interact to create larger amplitudes, tends to result in higher drag forces (Fig. 9a), which is more apparent when comparing vegetation tested under thinner network densities (Fig. 9b, c). High percentages of signal concentration tend to occur when the wave frequency is at a harmonic synchronization with the natural frequency of the element. The wake effects generated by the networks of vegetation located prior to the test element appear to reduce the occurrence of synchronization and are another difference between individual drag and bulk drag effects, but larger drag forces occur for vegetation with fewer resonant frequencies in the spectral density.

Fig. 9
figure 9

The percentage of torque spectral density signal occurring at the wave frequency compared to the drag force on the element for aluminum (X marker), straw (triangle marker), and foam (circle marker). a is for a dense canopy of vegetation, b is the medium canopy, and c is the thinnest of vegetation canopies upstream of the torque sensor

Full size image

We estimate the artificial vegetation natural frequency as a harmonic value wave frequency when the quotient of these two values is an integer value. A plot of the harmonic integer versus the percentage of torque spectral density at the wave frequency suggests that higher percentages occur at harmonic integers in the less flexible vegetation (Fig. 10), but there is not a strongly defensible trend. The three groupings of data by vegetation type in Fig. 10 result from the three vegetation types tested having different natural frequencies. The more flexible foam vegetation shows less harmonic influence than the more rigid vegetation having high percentages of spectral density at harmonic values, possibly due to increased deformation of the vegetation. The smaller foam mass may also result in more influence by the sensor natural frequency.

Fig. 10
figure 10

The artificial vegetation natural frequency divided by the water wave frequency is along the horizontal axis and the percentage of the spectral density signal occurring in the wave frequency

Full size image

The harmonic values and synchronization of vegetation movement with the wave period does appear to result in higher drag for the less flexible vegetation. The drag appears to be more substantially influenced by the flexibility of the vegetation, and the synchronization results in higher scatter in the data. Variations in the drag appear related to the oscillation frequency spectrum of the vegetation and in turn the hydroelastic behaviors and related vortex shedding frequencies. The drag differences can be explained if the higher harmonics of the wave frequencies and the natural frequencies of the vegetation resonate to reinforce the torque amplitude (Gabbi and Benaroya 2005).

These observations suggest that higher drag forces are possible when the driving wave frequency is close to the natural frequency of the system, as more energy can be transferred into the vegetation by constructive interference at these certain frequency bands. This phenomenon of synchronization occurs in many other systems and appears to be influential in the drag forces of vegetal elements as well. The natural frequency of the vegetation appears to be a key factor as to whether synchronization will occur, as well as the wake effects of other obstructions.

While it is possible to estimate a drag coefficient by taking a root mean square average of the time series data collected by assuming it has the form of a sine wave (Sorensen 2006), the experimental arrangement used herein allows for more direct analysis of the wave data. It does not appear possible to compare analyze the torque values collected at each time step however, and some averaging over longer time intervals of the drag coefficient is needed (Sarpaka and Isaacson 1981). The observed wave height for each discrete time interval allows calculation of the wave velocity from linear wave theory and comparison to the torque value measured for an instantaneous drag coefficient calculated from Eq. (6). This procedure results in extreme value singularity points due to the slight lag in the element torque response compared to the wave forces, so a torque is occurring for a null velocity, or a null torque value occurs when a velocity value is present.

A representative drag coefficient can be determined by the integration of the torque and velocity data using Eq. (5) over longer time intervals. The integrated drag coefficient value becomes stable when integration time intervals greater than a wave period are used, as shown in Fig. 11.

Fig. 11
figure 11

The integrated \(\tilde{C}_{D}\) average, maximum, and minimum values for different integration time durations. The driving wave had a period of 1 s

Full size image

Drag coefficients are commonly related to either the Re or KC (USACE 2006), using the orbital velocity and the vegetation diameter as the characteristic length. We calculated KC using the maximum orbital velocity, the wave period from the spectral analysis, and the vegetation diameter for the length scale. We have chosen to include a flexibility parameter consisting of the natural log of the modulus of elasticity of the vegetation divided by the natural log of a reference modulus of elasticity, taken as 100,000 Pa. The use of the reference elasticity does not significantly change the drag coefficient relationships, but does maintain the non-dimensionality of Re and KC in Figs. 12 and 13. Larger drag coefficients are noted at low Re and KC values. While low Re values suggest this is an area where inertial forces are more dominant, it is likely that inertial forces are dominating in the areas of low KC values as well. Additional experiments using materials with different mass but similar flexibility could further our understanding of this trend.

Fig. 12
figure 12

Drag coefficient, C D , as a function of KC, adjusted for the modulus of elasticity of the vegetation

Full size image
Fig. 13
figure 13

Drag Coefficient, C D , as a function of Re, adjusted for the modulus of elasticity of the vegetation

Full size image

Increases in drag of 60 % and greater have been reported (Sarpaka 1979) due to hydroelastic behavior and a similar effect appears to be occurring in some of the experiments of this study. The wave periods in our study ranged from 3 to 10 times greater than the Strouhal vortex shedding periods estimated for the vegetation, and so our experiments were likely to have cycles of vortex shedding in the lee side of the vegetation with oscillatory forces acting normal to flow (Sorensen 2006). The natural frequency divided by the Strouhal vortex shedding frequency was in the range of 1–1.4 for the experiments on aluminum and straws, which is a range found to result in synchronization (Sarpaka 1979). The experiments with foam were unlikely to have synchronization according to the natural frequency divided by the Strouhal vortex shedding frequency ratios were much greater than 1.4. The correlation plots for foam demonstrated complex signals, but due to the frequency value of 10 Hz, we believe this is influenced by the natural frequency of the sensor and not the vegetation.

While the torque response data provide insight into how the flexibility of vegetation can influence the drag, this experimental technique can also be used to calculate drag coefficients of the vegetation for use in wave dissipation applications. The analysis technique required is significantly more complex due to the time-varying flow velocities estimated through linear wave theory compared to the averaging needed for analysis when this instrumentation is used for unidirectional flow.

While this experiment did not include the larger wave periods and wave lengths sometimes found in nature, the vegetation scales well with field conditions. Larger wave periods and wave lengths will likely result in a greater intensity of vortex shedding and disturbances related to frequency.

5 Conclusion

The technique of attaching vegetation, or any obstruction, to a torque sensor is a simple and convenient way to gather data on force reactions in flow. These measurements allow us to efficiently measure the drag coefficient of different flexible obstructions or vegetation species and vegetation species at many stages of development without the need to establish an entire field of vegetation. When an entire field of vegetation is established, this technique can be used to understand the differences between individual drag and bulk drag. This technique also provides the frequency of loadings on the vegetation. The drag appears to be influenced by driving wave frequencies interacting with the vegetation, but the magnitude of the effect on drag appears to be also influenced by other factors such as flexibility of the vegetation. The more flexible vegetation results in less drag, indicating that the use of rigid obstruction data may not appropriate for understanding flexible vegetation. The drag and wave frequency interaction is also likely influenced by vegetation morphology, flexibility, and dampening characteristics. Generalized relationships of drag coefficients to Re and KC can be improved by incorporating a non-dimensional modulus of elasticity factor for flexible vegetation. The torque sensor represents a useful tool to more precisely measure the response of flexible vegetation to waves.