Abstract
Wall jets are important for a wide variety of engineering applications, including ventilation of confined spaces and cooling and drying processes. Although a lot of experimental studies have been devoted to wall jets, many of these have focused on laminar or turbulent wall jets. There is a lack of experimental data on transitional wall jets, especially transitional wall jets released into a confined space or enclosure. This paper presents flow visualizations and high-resolution Particle Image Velocimetry measurements of isothermal transitional plane wall jets injected through a rectangular slot in a confined space. As opposed to many previous studies, not only the wall jet region but also the recirculation region in the remainder of the enclosure is analyzed. The data and analysis in this paper provide new insights into the behavior of transitional plane wall jets in a confined space and will be useful for the validation of numerical simulations of this type of jets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The dynamics of air jets have been studied extensively in the past decades. Air jets are important for a wide range of engineering applications and are—among others—used for ventilation of buildings, ships and airplanes and for drying and cooling processes. Knowledge of the flow development and mixing characteristics of the jet is, therefore, of primary importance. Previous studies have dealt extensively with the development of turbulent round, plane and wall jets, both experimentally and numerically. However, to the knowledge of the authors, experiments on transitional jets are relatively scarce, especially for transitional plane wall jets issued into a confined space. Providing and analyzing such data are the main objectives of this paper. First, an overview of past studies on wall jets and transitional jets is provided. The findings from these studies will be used to support the analysis of the experiments in this paper.
A wall jet is a jet that is confined on one side by a wall. It can be subdivided in an inner region and an outer region. The inner region, or inner layer, runs from the wall to the point of maximum velocity U M and is similar to a wall boundary layer, whereas the outer region, or outer layer, consists of the remainder of the wall jet and can be seen as a free shear layer. A formal description of the wall jet is given by Launder and Rodi (1981): “A wall jet may be defined as a shear flow directed along a wall where, by virtue of the initially supplied momentum, at any station, the streamwise velocity over some region within the shear flow exceeds that in the external stream.” Wall jets can be subdivided in two-dimensional (plane) and three-dimensional wall jets. Plane wall jets are bounded by walls on the lateral sides of the jet, which prevent its lateral expansion, whereas three-dimensional wall jets can also grow in the lateral direction and are, therefore, more complex.
The first reported experimental study of a wall jet was conducted by Förthmann (1934). Later, turbulent wall jets were experimentally investigated by Bakke (1957), Sigalla (1958), Bradshaw and Gee (1960) and Schwarz and Cosart (1961). An extensive overview of experimental work until 1980 is given by Launder and Rodi (1981). Wygnanski et al. (1992), Hsiao and Sheu (1994, 1996), Gogineni and Shih (1997), Amitay and Cohen (1997), Eriksson et al. (1998) are just a few examples of studies in which the wall jet was experimentally analyzed during the last decades of the twentieth century.
A non-exhaustive overview of numerical work until the beginning of the 1980s is presented by Launder and Rodi (1983). After 1983, numerical work on wall jets has been performed by, among others, Conlon and Lichter (1995), Gogineni et al. (1999), Davidson et al. (2000), Bhattacharjee and Loth (2004), Wernz and Fasel (2007), Ahlman et al. (2009) and Balabel and El-Askary (2011). Note that unless mentioned otherwise, all studies mentioned above and below were conducted for wall jets in a more or less quiescent flow, that is, a flow domain that is large enough to prevent or minimize the disturbing effects of a secondary flow, which is in contrast to the studied flow pattern presented in this paper (Fig. 1).
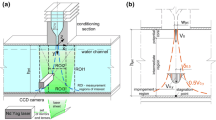
a Three-dimensional representation of the experimental setup, depicting the coordinate system, the inlet velocity U 0, the inlet height h, the outlet height h outlet and the dimensions of the test section L 3. b Two-dimensional schematic representation of the plane wall jet with I the inner region, II the outer region, U M the maximum velocity, y M the distance from the top wall to the location of U M , y C the distance from the bottom wall to the location of U M and y1/2 the location of 1/2U M in the outer region
Experimental and numerical analyses of turbulent wall jets in a confined space were reported by Moureh and Flick (2003, 2005). The focus of these studies was on the wall jet characteristics and its decay and detachment from the wall. The authors concluded that the separation of the wall jet from the top surface was caused by an adverse pressure gradient as a result of the confinement of the flow. The location of jet detachment experienced an intermittent behavior, since it oscillated around an average position (Moureh and Flick 2003). In this area, the velocity measurements were characterized by weak fluctuations in the order of 1 Hz. As a result of the intermittent behavior of the location of jet detachment, there was a dynamic interaction between the wall jet flow and the corner recirculation. Consequently, the zones occupied by these two flows expanded and narrowed at the rate of these fluctuations.
Although a lot of experimental studies have been performed for laminar and turbulent wall jets, only a few have focused on transitional wall jets. One of the first experimental studies on transitional plane wall jets was conducted by Bajura and Catalano (1975). They found that the transition from laminar to turbulent flow generally occurred in the following five stages: (1) formation of discrete vortices in outer region, (2) pairing of two or more vortices in the outer region, coupled with the possible pairing of vortex-like motions in the inner region wall boundary layer, (3) lifting-off of the wall jet flow into the ambient fluid, (4) dispersion of the lifted-off flow field by three-dimensional turbulent motions and (5) re-laminarization of the upstream flow, until another vortex pairing occurs. Lichter et al. (1992) experimentally analyzed the separation and vortex development of a wall jet in a stratified tank. They observed the organization of an asymmetric dipole after separation from the wall. Hsiao and Sheu (1994) studied the behavior of double row vortical structures in the near-field region of a plane wall jet. Flow visualizations and hot-wire measurements were performed to analyze vortex formation in the inner and outer region and vortex lift-off from the wall. Gogineni and Shih (1997) performed flow visualizations, Particle Image Velocimetry (PIV) and surface pressure measurements to study the vortex pairing and jet detachment associated with the transition of plane wall jets. From their measurements, they concluded that the boundary layer detaches from the wall as a result of a local adverse pressure gradient induced by the passage of a vortex structure in the outer region of the wall jet.
The studies discussed above were all conducted either for turbulent plane wall jets with or without confinement or for transitional plane wall jets without confinement, that is, which are not strongly influenced by a secondary flow. This is in contrast to the study in the present paper, in which a recirculation flow driven by a transitional wall jet dominates the flow in the remainder of the test section. To the knowledge of the authors, only a few studies have been conducted for transitional plane wall jets that are influenced by a secondary flow resulting from a restricted size of the test section (confined flow). Nielsen et al. (2000) and Topp et al. (2000) performed hot-sphere measurements of room air flow resulting from a plane wall jet at low Reynolds numbers. Wang and Chen (2009, 2010) performed point measurements of air flow in a simplified model of an airline cabin using hot-sphere and ultrasonic anemometers. The main objective of these measurements was to establish benchmark data to validate numerical flow simulations.
In addition to these wall jet studies, experiments were also performed for transitional flow in free plane jets (Sato 1960; Sato and Sakao 1964; Beavers and Wilson 1970; Mumford 1982; Lemieux and Oosthuizen 1985; Namer and Ötügen 1988). Namer and Ötügen (1988) stated that there is strong evidence that large vortical structures control the initial jet growth. Immediately downstream of the inlet, unstable laminar shear layers break down and form vortices that carry irrotational ambient fluid into the jet and thereby induce mixing by wrapping the ambient fluid about themselves. They also indicated the dependence of jet mixing, spread rate and centerline decay on the jet Reynolds number, but found that the Strouhal number, based on the vortex formation frequency in the outer region, was independent of Re for Re-values ranging from 1,000 to 7,000. Suresh et al. (2008) studied the transitional characteristics of plane jets for Re in the range from 250 to 6,250. They showed that jet spread decreases with Re due to the dominance of finer scales in higher Re jets and large-scale structures in the outer shear layer region for low Re jets (Re < 2,000). Furthermore, they concluded that the Strouhal number is Re-dependent for Re < 2,000. Additionally, transitional round jets were studied by Angioletti et al. (2003), O’Neill et al. (2004), Kwon and Seo (2005) and Todde et al. (2009).
Not only studies on transitional jets are relevant sources of information. Also studies of vortex dynamics in confined spaces can contribute to the understanding of vortex formation, advection and decay in an enclosure. For example, van Heijst et al. (1990) experimentally studied the spin-up process in a rectangular container. Konijnenberg et al. (1994) also studied the spin-up process in a rectangular tank, both experimentally and numerically. Wells et al. (2007) performed experiments and numerical simulations to investigate the production of small-scale vorticity near no-slip sidewalls of a container and to study the formation and decay of wall-generated quasi-two-dimensional vortical structures.
The present paper reports flow visualizations and PIV measurements of a transitional plane wall jet issued into a confined space. The study is motivated by the fact that most plane wall jet studies in the past have been conducted for plane wall jets in relatively large enclosures and/or with slot Reynolds numbers (i.e., Re based on inlet height) corresponding with a turbulent regime. As opposed to many previous studies, this study will not only focus on the wall jet region but also on the recirculation region in the remainder of the enclosure. One of the practical situations in which this type of flow is important is the ventilation of enclosures. The use of a wall jet to create a recirculation region that dilutes the air in a confined space is one of the two major ventilation principles that are used to maintain a healthy, energy-efficient and comfortable indoor climate in buildings, ships, planes, etc. (e.g., Nielsen 1974; Etheridge and Sandberg 1996; Awbi 2003; Chen 2009). In order to minimize the risk of discomfort of the occupants, velocities inside an enclosure should be kept relatively low. As a result, the jet flow might become transitional at these low velocities (low Re-values). First, the experimental setup is described in Sect. 2. The flow visualizations are addressed in Sect. 3. A description of the PIV measurement setup is given in Sect. 4, after which the results of the PIV measurements are analyzed in Sect. 5. Discussion (Sect. 6) and conclusions (Sect. 7) conclude this paper.
2 Experimental setup
A water-filled experimental model has been built to perform flow visualizations and PIV measurements (Fig. 1a). It consists of (1) a water column to drive the flow by hydrostatic pressure; (2) a flow conditioning section; (3) a cubic test section having edges of L = 0.3 m constructed from glass plates with a thickness of 8 mm; and (4) an overflow. The conditioning section in front of the inlet consists of one honeycomb, three screens and a contraction to obtain a uniform water flow at the inlet and to minimize the turbulence level. More information on the experimental setup can be found in van Hooff et al. (2012).
The coordinate system is made dimensionless: x′ = x/L, y′ = y/L, z′ = z/L (Fig. 1a). The inlet width (w) is 0.3 m (w′ = w/L = 1), and the dimensionless inlet height (h′ = h/L) can be varied from 0 to 0.1. For this study, h′ is fixed at 0.1. The height of the outlet is fixed at \( h_{outlet}^\prime \) = 0.0167. The slot Reynolds number is defined based on the inlet height as Re = Re slot = U 0 h/ν, with U 0 the area-averaged inlet velocity based on the volume flow rate through the inlet and ν the kinematic viscosity at room temperature (≈20°C). The maximum local velocity U M (Fig. 1b) is used to make the velocities non-dimensional (U/U M ). Note that U M is defined as the local maximum time-averaged x-velocity and thus varies with x. Furthermore, U M varies with Re; since Re is based on the inlet velocity U 0, the maximum velocities (U M ) are higher for higher values of Re. The distance from the top wall to the location of U M is \( y_M^\prime \) (=y M /L), whereas \( y_C^\prime \) = y C /L, with y C the distance from the bottom wall to the location of U M . The distance to the location of 1/2U M in the outer region is denoted as y 1/2. A useful quantity to characterize the flow in the midplane z′ = 0.5 is the z-component of the vorticity, defined as
which is non-dimensionalized as ω′ z = ω z h/U M . Finally, the Strouhal number is defined as St = (fh)/U M , with f the vortex formation frequency. In the remainder of the paper, dimensionless quantities will be used. The accent in the symbols will be dropped and the symbols will refer to the dimensionless quantities.
3 Flow visualizations
In general, flow visualization is performed to obtain qualitative information on the flow pattern. Several techniques are discussed in literature. Clayton and Massey (1967)—among others—provide an overview of methods that can be used to perform flow visualizations in water. One of the described methods, the injection of streaks of dye, was used in this study to provide some first qualitative information on the flow regime. The flow visualizations were performed by illuminating a fluorescent liquid that was injected in the flow field (Fig. 2a). To obtain a fluorescent liquid, fluorescein was dissolved in water until saturation of the solution was reached. The saturated solution was inserted in the flow field in the vertical center plane (z = 0.5) in front of the inlet using an injection needle with an outer diameter of 0.6 mm and a length of 80 mm (Fig. 2b). The needle diameter was kept as small as possible to minimize the disturbing effect of the needle on the flow. To illuminate the fluorescent solution, a slide projector was installed above the test section, providing a light sheet in the center of the water cube with a width of about 0.01 m, covering the entire test section of the cube (Fig. 2a). The flow pattern obtained by inserting and illuminating the fluorescent liquid was recorded with a video camera, and screen shots at a higher resolution were taken with a photo camera; both devices were positioned perpendicular to the flow direction as shown in Fig. 2a.
The flow visualizations were performed for Re ranging from 300 to 3,700. Figure 3 shows instantaneous images of the flow inside the enclosure, taken in the vertical center plane (z = 0.5), for Re ≈ 1,000, 1,750 and 2,500. Figure 3a shows that instabilities are present for Re ≈ 1,000. However, the presence of large-scale vortical structures cannot clearly be determined from the obtained instantaneous images. Clear large-scale vortical structures, however, can be distinguished in the outer region of the jet for the other two Re numbers (Fig. 3b, c). These vortices are due to instability of the free shear layer that is situated in the outer region of the wall jet. The vortical structures are convected downstream where they break up. From the flow visualizations, it can be concluded that transitional flow appears to be present for Re up to at least 2,500. Furthermore, it can be concluded that the onset of jet instability occurs further upstream as Re increases, which is in agreement with the findings of, among others, Kwon and Seo (2005). Note that this trend was observed from the unsteady evolution of the injected dye; this trend is not totally clear from the steady images depicted in Fig. 3. Based on the flow visualizations described in this section, PIV measurements were conducted for Re ranging from 300 to 2,500, which is the range for which transitional flow is present.
4 PIV measurement setup
The PIV measurements in this study were conducted using a two-dimensional PIV system consisting of a Nd:Yag (532 nm) double-cavity laser (2 × 200 mJ, repetition rate < 10 Hz) used to illuminate the field of view, and one CCD (charge-coupled device) camera (1,376 × 1,040 pixel resolution, max. 10 frames/s) for image acquisition. The laser was mounted on a translation stage and was positioned above the cubic test section to create a laser sheet in the vertical center plane of the cube; the CCD camera was positioned perpendicular to the laser sheet plane (Fig. 4). Seeding of the water was provided by hollow glass microspheres (3 M; type K1) with diameters in the range of 30–115 μm.
In order to determine the reliable time-averaged flow quantities, sufficient statistically-independent (uncorrelated) samples (i.e., PIV vector fields resulting from double image pairs) have to be acquired. Therefore, the PIV image acquisition frequency has to be sufficiently low. The required measuring frequency was estimated from the integral length scale (=inlet height) and the characteristic velocity (i.e., inlet velocity) and was set to the values shown in Table 1. Each measurement set consists of 360 uncorrelated samples. The errors associated with PIV measurements can be divided into systematic and repeatability errors. The systematic errors are present for each sample and consist of a range of errors that are associated with the PIV measurement technique and methodology (Prasad 2000). Prasad (2000) mentions 5 possible sources of errors (1) random error due to noise; (2) bias error; (3) gradient error; (4) tracking error; and (5) acceleration error. Due to the complexity of these errors, and the fact that a reduction in one error can lead to an increase in other errors, it is very difficult to provide a quantitative estimate of these errors on the measured velocity. To minimize the systematic errors, the best practice guidelines of Keane and Adrian (1990) and Prasad (2000) have been taken into account. The instantaneous PIV images were processed in two passes with decreasing interrogation areas, from 64 × 64 pixels to 32 × 32 pixels, both with a 75% overlap, to obtain instantaneous velocity vector fields. The vectors were only accepted when the ratio between the first and second tallest correlation peak for an interrogation area was above 1.3 to eliminate spurious vectors resulting from background noise or local insufficient seeding. The frame rate was chosen such that the particle displacement within an interrogation area between two frames was about 6 pixels, which satisfies the guidelines of Keane and Adrian (1990), who state that the particle displacement should be less than 1/4 of the interrogation area size. The particle diameter on the images was about 2 pixels, which is in accordance with the particle diameter as discussed in Prasad (2000). The repeatability, or random, error is a statistical error. The uncertainty associated with the repeatability error can be assessed using the central limit theorem (e.g., Coleman and Steel 1999). The random uncertainty of the mean velocity u r can be calculated with
with N the number of samples (in this case N = 360), z α/2 a variable related to the chosen confidence interval, r RMS the root mean square of the measured two-dimensional velocity in a point and R the mean two-dimensional velocity at the same location. For a confidence interval of 95%, the corresponding value of z α/2 = 1.96. The uncertainty of the measurement results is around 2–4% in the largest part of the test section and is slightly higher in the shear layer and boundary layer areas as a result of the locally higher turbulence levels. Note that R is the local two-dimensional velocity and not the maximum jet velocity in this case.
The two-dimensionality of the flow was tested by performing measurements in two additional vertical planes at z = 0.417 and z = 0.330, which showed no significant differences in the time-averaged flow pattern between the three vertical planes. The time-averaged velocity fields were obtained by averaging the 360 instantaneous velocity vector fields.
Two sets of PIV measurements were performed in the vertical center plane (z = 0.5) of the water cube. The first set focuses on the entire cross-section of the cube, that is, a region of interest (ROI) of L × L (Fig. 4; ROI1). The second set focuses on a smaller region of interest of 0.6 L × 0.4L (W × H) in the proximity of the inlet, enabling a higher measurement resolution (Fig. 4; ROI2). The higher resolution provides more detailed information in this area with expected large velocity gradients. This information about the inlet conditions is important as boundary conditions for future numerical simulations.
5 PIV measurement results
In this section, we will present and discuss the results of the PIV measurements. The results for the case with Re ≈ 300 are excluded because the observed flow pattern was very unstable, that is, the large recirculation region was not present in each instantaneous velocity vector field due to the very low momentum of the wall jet; therefore, averaging resulted in ambiguous results.
5.1 Analysis of time-averaged results
5.1.1 Time-averaged velocity vector fields
Figure 5 shows time-averaged velocity vector fields for Re ≈ 1,000, 1,750 and 2,500, for both sets of measurements. Note that only 1 out of 4 vectors is shown in all figures; that is, the actual resolution is sixteen times higher than shown. The velocity vectors are scaled with Re, and velocity vectors in the close vicinity of the inlet are omitted; due to reflections at the walls, the reliability of these vectors could not be guaranteed. Figure 5(a, c, e) show the large recirculation cell in the cube, which is driven by the wall jet. A smaller recirculation cell is present in the top right corner, and its size decreases with increasing Re. Figure 5(b, d, f) show the entrance of the wall jet and the presence of a very small recirculation cell just below the entrance. The size of this cell also decreases with increasing Re-values. Although the vector fields provide valuable information on the general flow pattern, for a more detailed analysis, profiles of time-averaged velocity, turbulence intensity and vorticity will be used.
5.1.2 Time-averaged velocity and turbulence profiles near the inlet
Figure 6 shows the profiles of dimensionless time-averaged x-velocity U/U M at distances x = 0.1, 0.2, 0.3, 0.4 and 0.5, in the vertical center plane (z = 0.5) for Re from 1,000 to 2,500. The coordinate system is given in Fig. 1. Figure 6a indicates that there are hardly any differences in the velocity profiles of the wall jet for the different Reynolds numbers at x = 0.1. However, the enlarged graph in Fig. 6f and the y C values in Fig. 7 show that the distance y C , measured from the bottom of the test section, increases slightly with increasing Re. Note that the small negative values at x = 0.1 (Fig. 6a) for low Re-values are caused by the small recirculation cell below the jet, as depicted in Fig. 5(b, d, f). The profiles beneath the outer region of the wall jet (y < 0.87) also show a dependency on Re; higher Re-values result in larger U/U M values below the outer region (Fig. 6a). The velocity profiles further downstream show an increasing dependence of the local wall jet behavior on Re; the differences in y C for the six different Re-values increase with increasing x (Fig. 7). Figure 6e, for example, shows that at x = 0.5, the position of maximum jet velocity lies at y C = 0.894 for Re ≈ 1,000, whereas y C = 0.944 for Re ≈ 2,500. The negative values of U/U M in Fig. 6e indicate jet detachment from the top surface for the lower Reynolds numbers (Re < 1,500); jet detachment at x = 0.5 is not yet present for higher Re, confirming that the location of jet detachment is Reynolds number dependent. Finally, Fig. 6(a, b) show a minimum value of U/U M below the outer region of the wall jet (at about y = 0.85) for x = 0.1 and x = 0.2.
The profiles of U/U M are compared with the theoretical profiles of an unconfined wall jet to study the influence of the confinement on the wall jet profiles. Figure 8 shows the profiles of U/U M at five distances (x = 0.1, 0.2, 0.3, 0.4, 0.5), as well as the theoretical profiles for a laminar wall jet (Glauert 1956) and for a turbulent wall jet (Verhoff 1963). Please note that the dimensionless y-coordinate is y/y 1/2 in this figure with y/y 1/2 = 0 at the top surface, instead of y with y = 1 at the top surface. The comparison for Re ≈ 1,000 in Fig. 8a shows that the velocity profiles are in relatively good agreement with the theoretical profile for a laminar wall jet. Especially, the location of maximum velocity is in good agreement with the theory for a laminar wall jet (y/y 1/2 ≈ 0.55), although the measured profiles have an almost top-hat profile instead of a parabolic profile. This different shape of the profile, especially at x = 0.1 and x = 0.2, is due to these measuring locations relatively close to the inlet, where the wall jet is not yet fully developed. At x = 0.5, the wall jet has developed into a parabolic profile, however, the maximum velocity is now located at a larger distance from the top surface compared to the profile of Glauert (1956). This discrepancy can be explained by the separation of the wall jet at x = 0.5 (U/U M < 0), caused by an adverse pressure gradient as a result of the flow confinement (downstream wall). Figure 8b compares the measured and the theoretical profiles for Re ≈ 1,750. It can be seen that the measured profiles are shifting upwards compared to the profiles at Re ≈ 1,000, as was also shown in Fig. 7. The profiles in the outer region of the wall jet resemble the theoretical profile of a laminar wall jet; however, in the inner region, the measured velocity profiles are now situated between the theoretical profiles for a laminar and a turbulent wall jet. The same holds for the location of maximum jet velocity (U/U M = 1), which is situated between the theoretical values of a laminar wall jet (y/y 1/2 ≈ 0.55) and of a turbulent wall jet (y/y 1/2 ≈ 0.15). Finally, Fig. 8c shows the comparison for Re ≈ 2,500, which is quite similar to the one for Re ≈ 1,750. The measured profiles in the outer region resemble the theoretical profile for a laminar wall jet to a large extent, whereas those in the inner region are moving even further upwards to the top surface and consequently also to the theoretical profile of a turbulent wall jet. Again, the velocity profiles close to the inlet are more or less top-hat shaped, indicating that the wall jet is not yet fully developed at these locations.
The longitudinal turbulence intensities u RMS/U M at x = 0.1 are shown in Fig. 9. The turbulence intensities in the core of the wall jet lie around 3% and do not show a clear tendency with Re. The turbulence intensities near the edges of the wall jet are higher due to the large velocity gradients as a result of the boundary layer and shear layer flows in the inner and outer region, respectively. The turbulence intensities in the outer region vary with Re: in general, an increase in Re results in an increase in turbulence intensity, although the turbulence intensity for Re ≈ 1,500 is lower than for Re ≈ 1,200, and the turbulence intensity for Re ≈ 2,500 is slightly lower than for Re ≈ 1,750 and Re ≈ 2,200. The general increase in turbulence intensity with increasing Re in the shear layer is caused by a higher velocity gradient between the wall jet and the recirculation zone, resulting in a higher turbulence level in this region. For the inner region, no clear tendency can be distinguished; the highest values are present for Re ≈ 1,000, while for Re ≈ 1,500 and Re ≈ 2,200, the lowest turbulence intensities are present. Therefore, it is not possible to draw any firm conclusions on the Re-dependency of the turbulence intensity in the inner region.
5.1.3 Time-averaged velocity profiles in the entire flow domain
The wall jet enters the confined space and forms a large recirculation zone that fills the cubical flow domain (Figs. 1a, 5a, c, e). Figure 10a shows profiles of the time-averaged non-dimensional x-velocity U/U M , taken at x = 0.2 for Re from 800 to 2,500. The profiles for different Re are almost identical in the near-wall region (y > 0.9), as also illustrated in Fig. 6b. In the outer region of the wall jet, the velocity decreases to values around U/U M = 0.05. Locally, in the region 0.8 < y < 0.9, a lower velocity is observed. Below this area of lower velocity, which was also depicted in Fig. 6b, U/U M shows an almost linear decrease to values around U/U M = −0.2 at y = 0.05. The profiles of U/U M are almost identical in the region from y = 0.6 to y = 0.2. Note that the profiles are not shown for y < 0.05. The results in this part of the cube are inaccurate due to reflections of the laser sheet on the glass bottom of the cube. In addition, note that small differences are present between the velocity profiles in Fig. 10a and in Fig. 6b (x = 0.2) below the wall jet (0.8 < y < 0.9). In this area, the velocities obtained from the measurements in ROI1 (Fig. 10a) are in general slightly lower than those obtained from ROI2 (Fig. 6b). The reason for this small discrepancy is the inability to accurately capture the small-scale recirculation zone just below the entrance of the wall jet due to the lower measuring resolution for ROI1. This recirculation zone directs the vertical flow along the upstream wall in the streamwise (x) direction, and as a result, the horizontal velocity component in this area increases. This flow feature is also clearly visible in Fig. 5(b, d, f) and briefly addressed in Sect. 5.1.1. However, the small recirculation cell below the entrance of the jet is not accurately detected in ROI1 (see Fig. 5a, c, e). As a result, the vertical flow along the upstream wall remains mainly vertical until it reaches the wall jet; the x-velocity remains relatively small, whereas the y-velocity is larger compared to the one measured at ROI2.
Profiles of U/U M at x = 0.5 are shown in Fig. 10b. As already shown in Fig. 6e, the profiles at x = 0.5 show Re-dependency in the wall jet region. The value of y C is lower for lower Re-values. From y = 0.6 to y = 0.1, U/U M decreases almost linearly from 0.15 to −0.2; again, no clear Re-dependency is present in this area. The height of the center of the recirculation zone, U/U M = 0, lies approximately at y = 0.4 for all Re-values.
Figure 10c shows U/U M at x = 0.8. Clear differences can be seen in the profiles for different Re. The negative values for U/U M in the inner region indicate detachment of the wall jet boundary layer, resulting in a small recirculation cell downstream of the detachment point. The size of this recirculation cell, and thus the area with negative values of U/U M , increases with decreasing Re. The vertical location of the maximum velocity depends strongly on Re, for example, for Re ≈ 1,000, y C = 0.754, whereas for Re ≈ 2,500, y C = 0.843. Below the wall jet region, y < 0.6, Re-dependency is still present, although the differences are far less pronounced.
5.1.4 Time-averaged vorticity profiles
Figure 11 shows profiles of z-vorticity ω z at x = 0.2 and x = 0.5 for seven different Re-values. The positive and negative ω z -values above and below y = 0.94 (Fig. 11a) clearly indicate the upper and lower parts of the jet, with dU/dy < 0 and dU/dy > 0, respectively (compare with Fig. 10a, b). Note that U/U M has the highest value at y = 0.94; at this location, ω z = 0, indicating the interface between positive and negative vorticity. The very weak negative vorticity in the range 0.1 < y < 0.8 is directly connected with the large clockwise-rotating recirculation cell. Figure 11a shows that there is no clear dependency of ω z on Re; below y = 0.94, the values of ω z are clearly Re-independent, whereas above y = 0.94, the values of ω z do not overlap, but also do not show a trend with Re. The vorticity distribution at x = 0.5 is depicted in Fig. 11b and shows roughly the same features as at x = 0.2. The border between the negative vorticity, induced by the shear layer, and the positive vorticity as a result of the boundary layer lies at y = 0.91 for Re-values until 1,200 and around y = 0.93 for Re > 1,200. From y = 0.75 until y = 0.1, a low and almost constant negative vorticity is present, which is associated with the clockwise-rotating recirculation cell extending over the lower part of the enclosure. Apparently, the motion in this cell is close to a rigid-body rotation. The differences in ω z for the different Re-values are more pronounced at x = 0.5 (Fig. 11b) than at x = 0.2. At x = 0.5, the locations of maximum ω z differ for different values of Re, which is consistent with the Re-dependent profiles of U/U M at this location, as indicated in Fig. 10b. Finally, the values of ω z in the jet region and below the jet region do not show a clear trend with Re.
5.2 Analysis of instantaneous flow field
5.2.1 Instantaneous velocity vector fields
The transient flow features are studied using instantaneous velocity vector fields. Figure 12 shows instantaneous velocity vector fields for Re ≈ 1,000, 1,750 and 2,500, at two different positions in time. Note that only 1 out of 2 vectors is shown; that is, the actual resolution is four times higher than shown. The velocity vectors are scaled with Re and the (mostly spurious) velocity vectors in the close vicinity of the inlet are not shown. A Kelvin–Helmholtz-type instability of the wall jet is clearly observed. Figure 13(a, c, e) show instantaneous vector fields for the same Re-values from the second measurement set with a reduced region of interest (ROI2). In this figure, only 1 out of 4 vectors is shown; that is, the actual resolution is sixteen times higher than shown, and the velocity vectors are again scaled with Re. Kelvin–Helmholtz-type instability waves are again visible at the outer region of the wall jet, which will grow and form the onset to the formation of discrete vortical structures. The presence of vortical structures is clearly visible in Fig. 13(b, d, f), which are obtained by subtracting the area-averaged instantaneous velocity from the absolute instantaneous velocities.
Instantaneous velocity vector fields. Absolute velocity vectors are depicted in panels (a, c, e), whereas (b, d, f) show the vector fields obtained by subtracting the area-averaged instantaneous velocity from the absolute instantaneous velocities. Re ≈ 1,000 (a, b), Re ≈ 1,750 (c, d), Re ≈ 2,500 (e, f)
5.2.2 Application of Q criterion
A further analysis of the vortical structures in the flow domain is conducted using the Okubo–Weiss function, which was independently defined by Okubo (1970) and Weiss (1991). Based on the Okubo–Weiss function, the Q criterion for the center plane (z = 0.5) can be defined as follows:
The first two terms denote the normal strain component and shear strain component, respectively, and the last term is associated with the vorticity ω z . Values of Q > 0 indicate strain dominated, hyperbolic, flow regions, whereas Q < 0 indicates rotation-dominated regions (elliptic flow regions). The Okubo–Weiss function is valid for two-dimensional flow and has been successfully used by, among others, Vosbeek et al. (1997), Isern-Fontanet et al. (2004), Molenaar et al. (2004) and Cieślik et al. (2010). In this study, Q is determined for the center x, y-plane (z = 0.5).
Figure 14 shows ω z contours and Q-contours for instantaneous velocity fields for Re ≈ 1,000, 1,750 and 2,500, respectively. Figure 14(a,c,e) show the vorticity distribution for the three values of Re, clearly illustrating the presence of vorticity in the inner and outer sides of the jet, associated with the boundary layer and the free shear layer, respectively. Figure 14(b, d, f) show the contours of Q, illustrating the presence of a vortex train in the outer region of the wall jet as a result of Kelvin–Helmholtz-type instability (shear layer). In the vortex train, one can distinguish rotation-dominated regions (Q < 0) alternating with strain-dominated regions (Q > 0). Figure 14(a, c, e) show that between the vortices, ω z ≈ 0; due to the strain in these regions, the resulting value of Q becomes positive (hyperbolic flow region) as depicted in Fig. 14(b, d, f). In contrast to the positive and negative Q-values in the outer region, the Q-values in the inner region lie around Q ≈ 0. In good approximation, the flow in the wall jet boundary layer is characterized by the absence of a vertical velocity component (v = 0) and a negligibly small horizontal velocity gradient ∂u/∂x, which indeed confirms that Q ≈ 0 in the inner region. However, Fig. 14b shows that for Re ≈ 1,000, a vortical structure is present in the inner region at x = 0.55 (Q < 0), which is a location downstream of the point of jet detachment (for Re ≈ 1,000: 0.4 < x < 0.5). This observation corresponds to those of Bajura and Catalano (1975) and Gogineni and Shih (1997) that the development of vortices in the outer region is followed by the development of vortices in the inner region of the wall jet, which occurs after detachment of the boundary layer from the wall due to an adverse pressure gradient. Furthermore, it can be concluded that there is an increase in the number of vortical structures per unit length for increasing Re-values, indicating an increased vortex formation frequency with increasing Re. As a result, the distance between the two consecutive vortical structures decreases with increasing Re.
The instantaneous velocity fields in combination with the knowledge on the presence of vortical structures in the outer region of the wall jet can be used to analyze the instantaneous velocity profiles of the wall jet. Figure 15 again shows the vortical structures in the outer region of the wall jet for Re ≈ 1,000. The dashed lines indicate the centers of the vortical structures in the outer region of the wall jet, whereas the solid line indicates a position between the two vortical structures. Figure 15b shows the instantaneous velocity profiles taken at the two dashed lines and the solid line. The minimum instantaneous x-velocity u/u M in the outer region of the wall jet is 0.208 at the line between the two vortical cores, while the minimum u/u M is 0.022 and 0.066 at the lines through vortex core 1 and vortex core 2, respectively. The presence of the clockwise-rotating vortical structures results in lower instantaneous values of u/u M in the outer region of the wall jet, to be more precise, at the location where the lower edges of the vortical structures are present.
5.2.3 Analysis of Strouhal number
Since a clear periodicity of the flow was observed, the relation between Re number and Strouhal number, defined as St = (fh)/U M , with f the vortex formation frequency, h the inlet height and U M the maximum x-velocity at x = 0.1, is analyzed in this section. This relation has been the subject of several studies in the past. Namer and Ötügen (1988), among others, analyzed the relationship between Re and St for free plane jets and Re ranging from 1,000 to 7,000. They stated that in their experiments, St was independent of the Re (St ≈ 0.273), even for Re = 1,000, which is expected to result in transitional flow. However, Suresh et al. (2008) did find a dependency of St on Re for free plane jets, at least for Re < 2,000. For higher Re, they found that St reached an asymptotic value of around 0.36. It should be noted that all studies described above were performed for free plane jets in an unconfined space.
The vortex formation frequency in this study was determined based on the average distance between two adjacent vortical structures and the local maximum jet velocity U M . Other studies reported vortex formation frequencies based on Fast Fourier Transformations (FFT); however, for the vast majority of the measurements in this study; the measuring frequency was too low (sampling frequency < Nyquist frequency) to be able to determine St using a frequency spectrum. Only for Re ≈ 1,000 and Re ≈ 1,200, the measuring frequency was high enough to apply FFT and to determine the vortex formation frequency. Comparison of FFT with the used method showed a good agreement between results from both methods (±5%).
Figure 16 shows the calculated St-values as a function of Re. The St-values clearly increase with increasing Re. The presented results partly agree with the findings of Suresh et al. (2008) that St increases with Re. However, in their case, St reached an asymptotic value at Re = 2,000, whereas no sign of an asymptotic value can be seen in Fig. 16 yet. A possible explanation might be the fact that the experiments in this study are all well within the transitional range and are consequently Re-dependent, whereas the onset to turbulent flow might have occurred at lower Re-values in the experiments by Suresh et al. (2008). Furthermore, their experiments were performed for a free jet and not for a wall jet and in air instead of water. Namer and Ötügen (1988) stated that the St-value, based on the vortex formation frequency, is constant. Our results, however, clearly show an increase in St with increasing Re (Fig. 16), in line with the findings of Suresh et al. (2008). Again, possible explanations might be the flow regime during the measurements (turbulent vs. transitional), and the fact that they studied free plane jets instead of confined plane wall jets. Furthermore, their study was conducted for an air jet.
6 Discussion
In this paper, the experimental results of a study on a transitional plane wall jet in a confined space have been presented and discussed. The experimental work consists of flow visualizations and PIV measurements to analyze the flow pattern. PIV measurements were performed for Reynolds numbers from 300 to 2,500, since the flow visualizations have shown that transitional flow is present for at least this range of Re-values.
In accordance with previous studies on transitional jets, the present study has shown that jet properties, such as time-averaged velocity, turbulence intensity and Strouhal number, show a Re-dependency. Unfortunately, a detailed comparison with previously published experimental data was not possible, since, to the knowledge of the authors, papers in which transitional plane wall jets in a confined space are analyzed using high-resolution measurements have not been published so far. However, a comparison with theoretical profiles was performed and showed that in general the measured wall jet profiles were situated between the theoretical profiles for a laminar and a turbulent wall jet. Furthermore, the comparison illustrated the effect of the flow confinement.
In Sect. 1, a short description was given of the five stages that generally occur during the transition from laminar to turbulent flow in jets, as identified by Bajura and Catalano (1975) based on flow visualizations and hot-film anemometry. In the present study, the presence of the following four stages can be identified: (1) formation of discrete vortices in the outer region (Figs. 13, 14), (2) formation of vortex-like motions in the inner region wall boundary layer (Fig. 14b), (3) separation of the wall jet from the top surface due to an adverse pressure gradient and (4) interaction of the separated wall jet with the global recirculation cell. Neither the vortex pairing in the inner and outer region nor the re-laminarization could be distinguished from the PIV measurements. The different observations are likely caused by the differences in experimental setup: the measurements in this study are performed in a confined space with an influence of the recirculation zone on the flow physics of the wall jet, whereas the measurements by Bajura and Catalano (1975) were conducted in an unconfined space, without influence of an opposing wall on the transition process. Furthermore, the measurement resolution and frequency in our study might have been too low to capture the pairing of vortices in the test section.
In addition, there are some other limitations concerning the experimental work described in this paper. First, the reflections of the glass bottom of the test section made it impossible to analyze the flow in this area of the cube. As a result, some information on the flow pattern is lacking, although one must note that the bottom of the cube is not the primary area of interest in this study, in contrast to the wall jet region. Second, the determination of the Strouhal number has not been conducted using FFT, although the suitability of the used method has been assessed using FFT. Future work should consist of measurements with a higher temporal resolution (time-resolved measurements) to enable the use of more accurate methods to determine the Strouhal number. Finally, there appears to be a small discrepancy between the velocity profiles obtained from the higher resolution measurements in the vicinity of the inlet and the profiles obtained from the measurements in the entire cross-section of the cube. The second set of profiles (Fig. 6) indicates the presence of a top-hat profile, which is not that clearly visible in the profiles obtained from the second set of measurements (Fig. 10). Furthermore, the values of U/U M below the entrance of the wall jet show small differences between ROI1 and ROI2. A possible explanation for these small deviations is the lower measuring resolution for the measurements in the entire cross-section of the cube (ROI1), in combination with relatively smaller seeding due to the larger field of view.
This study is a first step in a more extensive research project on transitional wall jets in a confined space. Future work will include measurements for different inlet opening heights h, inlet geometries and additional values of the slot Reynolds number Re = U 0 h/ν. Alongside the PIV measurements, point measurements will be conducted using Laser Doppler Anemometry (LDA). These point measurements in an air filled setup (2 × 2 × 2 m3) will provide time-resolved data of the air flow pattern, which will provide valuable complementary information to the data set presented in this paper. In addition, LDA is more suited than PIV to carry out a local study concerning wall jet detachment, especially its intermittency (Moureh and Flick 2003) and the local turbulence anisotropy (Moureh and Flick 2005).
7 Conclusions
This paper presents a detailed and systematic experimental analysis of a transitional plane wall jet in a confined space. To ensure that the measurements are conducted for a transitional flow regime, flow visualizations have been performed using fluorescent dye. Based on the flow visualizations, PIV measurements have been conducted for seven Reynolds numbers, ranging from 800 to 2,500. For each value of Re, two sets of measurements have been obtained: one of the flow pattern in the entire cross-section of the cube (region of interest = L × L) and one with a smaller region of interest near the inlet (0.6L × 0.4L) to increase the measurement resolution in this area with large velocity gradients. Both the time-averaged and the instantaneous vector fields have been analyzed.
From the time-averaged results, the following conclusions can be made:
-
The flow visualizations and the PIV measurements have indicated that the onset of jet instability occurs further downstream as Re increases.
-
The general flow pattern is the same for all tested Re-values (800 < Re < 2,500). The wall jet drives the large recirculation cell in the center of the cube. Smaller recirculation cells are present in the downstream top corner and just below the jet entrance in the enclosure.
-
The size of these small recirculation cells decreases with increasing Re.
-
The velocity profiles show a clear Re-dependency that increases with increasing distance from the inlet.
-
Jet detachment and the location of maximum jet velocity (y C ) both depend on Re; the jet detachment occurs further downstream and y C increases with increasing Re.
-
The wall jet is not yet fully developed at small distances from the inlet, while at larger distances from the inlet, the confinement of the jet and the associated adverse pressure gradient lead to flow separation and a reversed flow.
-
The outer region of the measured wall jet resembles the theoretical values for a laminar wall jet for all tested Re-values. The inner region for Re ≈ 1,000 also shows a fair to good agreement with the laminar wall jet. For Re ≈ 1,750 and Re ≈ 2,500, however, the velocity profiles in the inner region are shifting toward the theoretical values of a turbulent wall jet.
-
Below the wall jet region, the dimensionless vorticity profiles are Re-independent, whereas in the wall jet region, the values of ω z do not overlap, but also do not show a trend with Re.
-
The large velocity gradients in the inner and outer region of the wall jet due to the boundary layer and the shear layer result in increased values of positive and negative z-vorticity, respectively. The weak negative vorticity in the center of the test section is associated with the large clockwise-rotating recirculation cell, and the uniform ω z -value indicates a solid-body rotation in this cell.
Analysis of the instantaneous velocity vector fields has led to the following conclusions:
-
Kelvin–Helmholtz-type instability waves are present at the bottom part of the wall jet, which grow and lead to the formation of discrete vortical structures in the outer region.
-
The Q criterion shows that the positive vorticity in the inner region, and before jet detachment, is the result of shear in the boundary layer (hyperbolic region). However, in the outer region, a vortex train is present with alternating regions of Q < 0 and Q > 0, indicating the presence of rotation-dominated regions (elliptic flow) and strain-dominated regions (hyperbolic flow), respectively.
-
The instantaneous velocity profiles indicate a lower velocity in the outer region of the wall jet at the locations of the vortical structures. This feature is due to the presence of clockwise-rotating coherent structures, the bottom of which causes the locally lower values of the instantaneous velocity.
-
The number of formed vortices per unit length increases with Re, and this increase is larger than the increase in inlet velocity; therefore, the Strouhal number St increases with an increase in Re.
References
Ahlman D, Velter G, Brethouwer G, Johansson AV (2009) Direct numerical simulation of nonisothermal turbulent wall jets. Phys Fluids 21:035101
Amitay M, Cohen J (1997) Instability of a two-dimensional plane wall jet subjected to blowing or suction. J Fluid Mech 344:67–94
Angioletti M, Di Tomasso RM, Nino E, Ruocco G (2003) Simultaneous visualization of flow field and evaluation of local heat transfer by transitional impinging jets. Int J Heat Mass Transfer 46:1703–1713
Awbi HB (2003) Ventilation of buildings. Spon Press, London
Bajura RA, Catalano MR (1975) Transition in a two-dimensional plane wall jet. J Fluid Mech 70:773–799
Bakke P (1957) An experimental investigation of a wall jet. J Fluid Mech 2:467–472
Balabel A, El-Askary WA (2011) On the performance of linear and nonlinear k–ε turbulence models in various jet flow applications. Eur J Mech B Fluids 30:325–340
Beavers GS, Wilson TA (1970) Vortex growth in jets. J Fluid Mech 44:97–112
Bhattacharjee P, Loth E (2004) Simulations of laminar and transitional cold wall jets. Int J Heat Fluid Flow 25:32–43
Bradshaw P, Gee MT (1960) Turbulent wall jets with and without an external stream. Aeronautical Research Council R&M 3252
Chen Q (2009) Ventilation performance prediction for buildings: A method overview and recent applications. Build Environ 44:848–858
Cieślik AR, Kamp LPJ, Clercx HJH, van Heijst GJF (2010) Three-dimensional structures in a shallow flow. J Hydro-Environ Res 4:89–101
Clayton BR, Massey BS (1967) Flow visualization in water: a review of techniques. J Sci Instrum 44:2–11
Coleman HW, Steel WG (1999) Experimentation and uncertainty analysis for engineers. Wiley, New York
Conlon BP, Lichter S (1995) Dipole formation in the transient planar wall jet. Phys Fluids 7:999–1014
Davidson L, Nielsen PV, Topp C (2000) Low Reynolds number effects in ventilated rooms: a numerical study. Proc. of Roomvent 2000, Oxford: 307–312
Eriksson JG, Karlsson RI, Persson J (1998) An experimental study of a two-dimensional plane turbulent wall jet. Exp Fluids 25:50–60
Etheridge DW, Sandberg M (1996) Building ventilation: theory and measurement. Wiley, London
Förthmann E (1934) Über turbulente strahleausbreitung. Ing Archiv 5:42–54
Glauert P (1956) The wall jet. J Fluid Mech 1:625–643
Gogineni S, Shih C (1997) Experimental investigation of the unsteady structure of a transitional plane wall jet. Exp Fluids 23:121–129
Gogineni S, Visbal M, Shih C (1999) Phase-resolved PIV measurements in a transitional plane wall jet: a numerical comparison. Exp Fluids 27:126–136
Hsiao FB, Sheu SS (1994) Double row vortical structures in the near field region of a plane wall jet. Exp Fluids 17:291–301
Hsiao FB, Sheu SS (1996) Experimental studies on flow transition of a plane wall jet. Aeronaut J100(999):373–380
Isern-Fontanet J, Font J, García-Ladona E, Emelianov M, Millot C, Taupier-Letage I (2004) Spatial structures of anticyclonic eddies in the Algerian basin (Mediterranean Sea) analyzed using the Okubo-Weiss parameter. Deep Sea Res II 51:3009–3028
Keane RD, Adrian RJ (1990) Optimization of particle image velocimeters. Part I: double pulsed systems. Meas Sci and Technol 1:1202–1215
Konijnenberg JA, Andersson HI, Billdal JT, van Heijst GJF (1994) Spin-up in a rectangular tank with low angular velocity. Phys Fluids 6:1168–1176
Kwon SJ, Seo IW (2005) Reynolds number effects on the behavior of a non-buoyant round jet. Exp Fluids 38:801–812
Launder BE, Rodi W (1981) The turbulent wall jet. Prog Aerospace Sci 19:81–128
Launder BE, Rodi W (1983) The turbulent wall jet—measurements and modelling. Annu Rev Fluid Mech 15:429–459
Lemieux GP, Oosthuizen PH (1985) Experimental study of the behavior of plane turbulent jets at low Reynolds numbers. AIAA J 23:1845–1846
Lichter S, Flór JB, van Heijst GJF (1992) Modelling the separation and eddy formation of coastal currents in a stratified tank. Exp Fluids 13:11–16
Molenaar D, Clercx HJH, van Heijst GJF (2004) Angular momentum of forced 2D turbulence in a square no-slip domain. Phys D 196:329–340
Moureh J, Flick D (2003) Wall air-jet characteristics and airflow patterns within a slot ventilated enclosure. Int J Therm Sci 42:703–711
Moureh J, Flick D (2005) Airflow characteristics within a slot-ventilated enclosure. Int J Heat Fluid Flow 26:12–24
Mumford JC (1982) The structure of the large scale eddies in fully developed turbulent shear flows. Part 1. The plane jet. J Fluid Mech 116:241–268
Namer I, Ötügen MV (1988) Velocity measurements in a plane turbulent air jet at moderate Reynolds numbers. Exp Fluids 6:387–399
Nielsen PV (1974) Flow in air conditioned rooms, PhD Thesis, Technical University of Denmark, Copenhagen
Nielsen PV, Filholm C, Topp C, Davidson L (2000) Model experiments with low Reynolds number effects in a ventilated room. Proc. of Roomvent, Oxford: 185–190
O’Neill P, Soria J, Honnery D (2004) The stability of low Reynolds number round jets. Exp Fluids 36:473–483
Okubo A (1970) Horizontal dispersion of floatable trajectories in the vicinity of velocity singularities such as convergencies. Deep-Sea Res 17:445–454
Prasad AK (2000) Particle image velocimetry. Curr Sci 79:51–60
Sato H (1960) The stability and transition of a two-dimensional jet. J Fluid Mech 7:53–80
Sato H, Sakao F (1964) An experimental investigation of the instability of a two-dimensional jet at low Reynolds numbers. J Fluid Mech 20:337–352
Schwarz WH, Cosart WP (1961) The two-dimensional wall jet. J Fluid Mech 10:481–495
Sigalla A (1958) Measurements of skin friction in a plane turbulent wall jet. J Royal Aero Soc 62:873–877
Suresh PR, Srinivasan K, Sundararajan T, Das SK (2008) Reynolds number dependence of plane jet development in the transitional regime. Phys Fluids 20:044105–044105-12
Todde V, Spazzini PG, Sandberg M (2009) Experimental analysis of low-Reynolds number free jets: evolution along the jet centerline and Reynolds number effects. Exp Fluids 47:279–294
Topp C, Nielsen PV, Davidson L (2000) Room airflows with low Reynolds number effects. Proc. of Roomvent, Oxford: 541–546
van Heijst GJF, Davies PA, Davis RG (1990) Spin-up in a rectangular container. Phys Fluids 2:150–159
van Hooff T, Blocken B, Defraeye T, Carmeliet J, van Heijst GJF (2012) PIV measurements and analysis of transitional flow in a reduced-scale model: ventilation by a free plane jet with Coanda effect. Build Environ. http://dx.doi.org/10.1016/j.buildenv.2012.03.020
Verhoff A (1963) The two-dimensional turbulent wall jet with and without an external stream Report 626. Princeton University, New Jersey
Vosbeek PWC, van Geffen JHGM, Meleshko VV, van Heijst GJF (1997) Collapse interactions of finite-sized two-dimensional vortices. Phys Fluids 9:3315
Wang M, Chen Q (2009) Assessment of various turbulence models for transitional flows in enclosed environment. HVAC&R Res 15:1099–1119
Wang M, Chen Q (2010) On a hybrid RANS/LES approach for indoor airflow modelling. HVAC&R Res 16:731–747
Weiss J (1991) The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Phys D 48:273–294
Wells MG, Clercx HJH, van Heijst GJF (2007) Vortices in oscillating spin-up. J Fluid Mech 573:339–369
Wernz S, Fasel HF (2007) Nonlinear resonances in a laminar wall jet: ejection of dipolar vortices. J Fluid Mech 588:279–308
Wygnanski I, Katz Y, Horev E (1992) On the applicability of various scaling laws to the turbulent wall jet. J Fluid Mech 234:669–690
Acknowledgments
Twan van Hooff is currently a PhD student funded by both Eindhoven University of Technology in the Netherlands and Fonds Wetenschappelijk Onderzoek (FWO)—Flanders, Belgium (FWO project number: G.0435.08). The FWO Flanders supports and stimulates fundamental research in Flanders. Its contribution is gratefully acknowledged. Thijs Defraeye is a postdoctoral fellow of the FWO—Flanders and acknowledges its support. The measurements reported in this paper were supported by the Laboratory of the Unit Building Physics and Services (BPS) at Eindhoven University of Technology and the Laboratory of Building Physics at the Katholieke Universiteit Leuven. Special thanks go to Jan Diepens, head of LBPS, and Wout van Bommel, Harrie Smulders, Geert-Jan Maas and Peter Cappon, members of the LBPS, for their valuable contributions.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
van Hooff, T., Blocken, B., Defraeye, T. et al. PIV measurements of a plane wall jet in a confined space at transitional slot Reynolds numbers. Exp Fluids 53, 499–517 (2012). https://doi.org/10.1007/s00348-012-1305-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00348-012-1305-5