Skip to main content
SpringerLink
Log in

Effect of finite cavity width on flow oscillation in a low-Mach-number cavity flow

  • Research Article
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

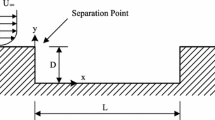
The current study is focused on examining the effect of the cavity width and side walls on the self-sustained oscillation in a low Mach number cavity flow with a turbulent boundary layer at separation. An axisymmetric cavity geometry is employed in order to provide a reference condition that is free from any side-wall influence, which is not possible to obtain with a rectangular cavity. The cavity could then be partially filled to form finite-width geometry. The unsteady surface pressure is measured using microphone arrays that are deployed on the cavity floor along the streamwise direction and on the downstream wall along the azimuthal direction. In addition, velocity measurements using two-component Laser Doppler Anemometer are performed simultaneously with the array measurements in different azimuthal planes. The compiled data sets are used to investigate the evolution of the coherent structures generating the pressure oscillation in the cavity using linear stochastic estimation of the velocity field based on the wall-pressure signature on the cavity end wall. The results lead to the discovery of pronounced harmonic pressure oscillations near the cavity’s side walls. These oscillations, which are absent in the axisymmetric cavity, are linked to the establishment of a secondary mean streamwise circulating flow pattern near the side walls and the interaction of this secondary flow with the shear layer above the cavity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  • Adrian JR (1979) Conditional eddys in isotropic turbulence. Phys Fluids 22:2065–2070

    Article  MATH  Google Scholar 

  • Adrian JR (1983) Fluid mechanics measurements, chap 5: laser velocimetry. Taylor and Francis, Bristol, pp 157–159

    Google Scholar 

  • Ahuja KK, Mendoza J (1995) Effects of cavity dimensions, boundary layer, and temperature on cavity noise with emphasis on benchmark data to validate computational aeroacoustic codes. Contractor report 4653, National Aeronautics and Space Administration

  • Ashcroft G, Zhang X (2005) Vortical structures over rectangular cavities at low speed. Phys Fluids 17(015104):1–8

    Google Scholar 

  • Block PJW (1976) Noise response of cavities of varying dimensions at subsonic speeds. Technical notes D-8351, National Aeronautics and Space Administration

  • Bres GA, Colonius T (2008) Three-dimensional instability in compressible flow over open cavities. J Fluid Mech 599:309–339

    Article  MATH  Google Scholar 

  • Cattafesta L, Williams D, Rowley C, Alvi F (2003) Review of active control of flow-induced cavity resonance. AIAA paper 2003–3567

  • Charwat AF, Roos JN, Dewey FC, Hitz JA (1961) An investigation of separated flows. Part 1. The pressure field. J Aerosp Sci 28:457–470

    MATH  Google Scholar 

  • Faure TM, Pastur L, Lusseyran F, Fraigneau Y, Bisch D (2009) Three-dimensional centrifugal instabilities development inside a parallelepipedic open cavity of various shape. Exp Fluids 47:395–410

    Article  Google Scholar 

  • Gharib M, Roshko AF (1987) The effect of flow oscillations on cavity drag. J Fluid Mech 177:501–530

    Article  Google Scholar 

  • Grace SM, Dewar GW, Wroblewski DE (2004) Experimental investigation of the flow characteristics within a shallow wall cavity for both laminar and turbulent upstream boundary layers. Exp Fluids 36:791–804

    Article  Google Scholar 

  • Guezennec YG (1989) Stochastic estimation of coherent structures in turbulent boundary layer. Phys Fluids A 1:1054–1060

    Article  MathSciNet  Google Scholar 

  • Larcheveque L, Sagaut P, Le T, Comte P (2004) Large-eddy simulation of a compressible flow in a 3-D open cavity at high Reynolds number. J Fluid Mech 516:265–301

    Article  MATH  Google Scholar 

  • Martin WW, Naudascher E, Padmanabhan M (1975) Fluid-dynamic excitation involving flow instability. J Hydraul Div, Am Soc Civ Eng 101(HY6):681–698

    Google Scholar 

  • Maull DJ, East LF (1963) Three-dimensional flow in cavities. J Fluid Mech 16:620–632

    Article  MATH  Google Scholar 

  • Migeon C (2002) Details on the start-up development of the Taylor-Gortler-like vortices inside a square-section lid-driven cavity for 1,000 ≤ Re ≤ 3,200. Exp Fluids 33:594–602

    Google Scholar 

  • Morris SC, Foss JF (2003) Turbulent boundary layer to single-stream shear layer: the transition region. J Fluid Mech 494:187–221

    Article  MATH  Google Scholar 

  • Murray N, Ukeiley L (2003) Estimation of the flow field from surface pressure measurements in an open cavity. AIAA J 41(5):969–972

    Article  Google Scholar 

  • Murray N, Ukeiley L (2007) Modified quadratic stochastic estimation of resonating subsonic cavity flow. J Turbul 8(53):1–14

    Google Scholar 

  • Najm HN, Ghoniem AF (1991) Numerical simulation of the convective instability in a dump combustor. AIAA J 29(6):911–919

    Article  Google Scholar 

  • Ozsoy E, Rambaud P, Riethmuller ML (2005) Vortex characteristics in laminar cavity flow at very low Mach number. Exp Fluid 38:133–145

    Article  Google Scholar 

  • Plumbee HE, Gibson JS, Lassiter LW (1962) A theoretical and experimental investigation of the acoustic response of cavities in an aerodynamic flow. Technical report WADD-TR-61–75, US Air Force

  • Rockwell D (1977) Prediction of oscillation frequencies for unstable flow past cavities. J Fluids Eng 199:294–300

    Article  Google Scholar 

  • Rockwell D, Knisely C (1980) Observations of the 3-D nature of unstable flow past a cavity. Phys Fluids 23(3):425–431

    Article  Google Scholar 

  • Rockwell D, Naudascher E (1978) Review: self-sustaining oscillations of flow past cavities. Trans ASME: J Fluids Eng 100:152–165

    Article  Google Scholar 

  • Rossiter JE (1964) Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Technical report 3438, aeronautical research council reports and memoranda

  • Rowley CW, Williams DR (2006) Dynamics and control of high-Reynolds-number flow over open cavities. Annu Rev Fluid Mech 38:251–276

    Article  MathSciNet  Google Scholar 

  • Rowley CW, Colonius T, Basu AJ (2002) On self-sustained oscillations in 2-D compressible flow over rectangular cavities. J Fluid Mech 455:315–346

    Article  MathSciNet  MATH  Google Scholar 

  • Sarohia V (1977) Experimental investigation of oscillations in flows over shallow cavities. AIAA J 15(7):984–991

    Article  Google Scholar 

  • Shankar PN, Deshpande MD (2000) Fluid mechanics in the driven cavity. Annu Rev Fluid Mech 32:93–136

    Article  MathSciNet  Google Scholar 

  • Ukeiley L, Murray N (2005) Velocity and surface pressure measurements in an open cavity. Exp Fluids 38:656–671

    Article  Google Scholar 

  • Zhang K, Naguib AM (2006) Dispersion relation and mode selectivity in low-mach-number cavity flows. AIAA paper 2006–3229

  • Zhang K, Naguib AM (2008) Effect of cavity width on the unsteady pressure in a low-mach-number cavity. AIAA J 46(7):1878–1880

    Article  Google Scholar 

Download references

Acknowledgments

This work was sponsored by a grant through the National Science Foundation (grant number CTS-0425374). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. The leading author is also grateful for the support by Zonta International through the Amelia Earhart fellowship.

Author information

Authors and Affiliations

  1. Michigan State University, East Lansing, MI, 48824, USA

    Ke Zhang & Ahmed M. Naguib

Authors
  1. Ke Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmed M. Naguib
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed M. Naguib.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, K., Naguib, A.M. Effect of finite cavity width on flow oscillation in a low-Mach-number cavity flow. Exp Fluids 51, 1209–1229 (2011). https://doi.org/10.1007/s00348-011-1142-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00348-011-1142-y

Keywords

Search

Navigation