Skip to main content
SpringerLink
Log in

Comparison of three roughness function determination methods

  • Original
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

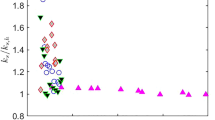
Three methods have been used to experimentally determine the roughness function (ΔU +) for several rough surfaces. These include the rotating disk, the towed plate, and the velocity profile methods. The first two are indirect methods in as much as they rely on measurements of overall torque or resistance and boundary layer similarity laws to obtain ΔU +, whereas the velocity profile method provides a direct measurement of ΔU +. The present results indicate good agreement between the towed plate and the velocity profile methods for all of the surfaces tested. Tests for the rotating disk were carried out at much higher unit Reynolds numbers. Using this method, the results for sandpaper rough surfaces agree within their uncertainty with a Nikuradse-type roughness function in the fully rough regime, while a spray painted surface agrees with a Colebrook-type roughness function.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.

Similar content being viewed by others

Abbreviations

B :

smooth wall log-law intercept, =5.0

C F :

overall frictional resistance coefficient, \( = {{\left( {F_{{\text{D}}} } \right)}} \mathord{\left/ {\vphantom {{{\left( {F_{{\text{D}}} } \right)}} {{\left( {\tfrac{1} {2}\rho U_{{\text{e}}} ^{2} S} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {\tfrac{1} {2}\rho U_{{\text{e}}} ^{2} S} \right)}} \)

C f :

skin-friction coefficient, \( = {{\left( {\tau _{{\text{o}}} } \right)}} \mathord{\left/ {\vphantom {{{\left( {\tau _{{\text{o}}} } \right)}} {{\left( {\tfrac{1} {2}\rho U_{{\text{e}}} ^{2} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {\tfrac{1} {2}\rho U_{{\text{e}}} ^{2} } \right)}} \)

C m :

torque coefficient, =(2M)/(ρR 5(φω)2)

F D :

drag force

k :

arbitrary measure of roughness height

K :

acceleration parameter, \( = \frac{\nu } {{U^{2}_{{\text{e}}} }}\frac{{{\text{d}}U_{{\text{e}}} }} {{{\text{d}}x}} \)

L :

plate length

M :

torque

N :

number of samples or replicates

R :

disk radius

R a :

centerline average roughness height, \( = \frac{1} {N}{\sum\limits_{i = 1}^N {{\left| {y_{i} } \right|}} } \)

R q :

root mean square roughness height, \( = {\sqrt {\frac{1} {N}{\sum\limits_{i = 1}^N {y^{2}_{i} } }} } \)

R t :

maximum peak to through height, =y max−y min

R z :

ten point roughness height, \( = {\sum\limits_{i = 1}^5 {{\left( {y_{{\max i}} - y_{{\min i}} } \right)}} } \)

Re L :

Reynolds number based on plate length, =U e L/ν

Re R :

Reynolds number based on disk radius, =φωR 2/ν

Re θ :

momentum thickness Reynolds number, =U e θ/ν

S :

wetted surface area

U :

mean velocity in the x direction

U e :

freestream velocity relative to surface

U τ :

friction velocity, \( = {\sqrt {{\tau _{{\text{o}}} } \mathord{\left/ {\vphantom {{\tau _{{\text{o}}} } \rho }} \right. \kern-\nulldelimiterspace} \rho } } \)

u′:

streamwise fluctuating velocity

ν′:

wall-normal fluctuating velocity

x :

streamwise distance from plate leading edge

y :

normal distance from the boundary

δ :

boundary layer thickness

ΔU + :

roughness function

ΔU +′:

roughness function slope, =d(ΔU +)/d(lnk +)

ε :

wall datum offset

φ :

swirl factor, \( = {{\left( {\frac{1} {{{\sqrt {C_{{\text{m}}} } }}}} \right)}_{\infty } } \mathord{\left/ {\vphantom {{{\left( {\frac{1} {{{\sqrt {C_{{\text{m}}} } }}}} \right)}_{\infty } } {{\left( {\frac{1} {{{\sqrt {C_{{\text{m}}} } }}}} \right)}_{{{\text{en}}}} }}} \right. \kern-\nulldelimiterspace} {{\left( {\frac{1} {{{\sqrt {C_{{\text{m}}} } }}}} \right)}_{{{\text{en}}}} } \)

κ :

von Kármán constant, =0.41

ν :

kinematic viscosity of the fluid

Π :

wake parameter

θ :

momentum thickness, \( = {\int\limits_0^\delta {{\left( {1 - \frac{U} {{U_{{\text{e}}} }}} \right)}^{2} {\text{d}}y} } \)

ρ :

density of the fluid

τ o :

wall shear stress

ω :

angular velocity

+:

inner variable (normalized with U τ or U τ /ν)

en:

disk rotating in enclosed tank

min:

minimum value

max:

maximum value

R:

rough surface

S:

smooth surface

∞:

disk rotating in unconfined fluid

References

  • Acharya M, Bornstein J, Escudier MP (1986) Turbulent boundary layers on rough surfaces. Exp Fluids 4:33–47

    CAS  Google Scholar 

  • Antonia RA, Krogstad P-Å (2001) Turbulence structure in boundary layers over different types of surface roughness. Fluid Dynam Res 28:139–157

    Article  Google Scholar 

  • Clauser FH (1954) Turbulent boundary layers in adverse pressure gradients. J Aeronaut Sci 21:91–108

    Google Scholar 

  • Colebrook CF (1939) Turbulent flow in pipes with particular reference to the transition between smooth and rough pipe laws. J Civil Eng 11:133–157

    Google Scholar 

  • Coleman HW, Steele WG (1995) Engineering application of experimental uncertainty analysis. AIAA J 33:1888–1896

    Google Scholar 

  • Coles D (1962) The turbulent boundary layer in a compressible fluid. Report R-403-PR, The Rand Corp.

  • Granville PS (1958) The frictional resistance and turbulent boundary layer of rough surfaces. J Ship Res 1:52–74

    Google Scholar 

  • Granville PS (1982) Drag-characterization method for arbitrarily rough surfaces by means of rotating disks. J Fluids Eng 104:373–377

    Google Scholar 

  • Granville PS (1987) Three indirect methods for the drag characterization of arbitrarily rough surfaces on flat plates. J Ship Res 31:70–77

    Google Scholar 

  • Grigson CWB (1992) Drag losses of new ships caused by hull finish. J Ship Res 36:182–196

    Google Scholar 

  • Hama FR (1954) Boundary-layer characteristics for rough and smooth surfaces. Trans SNAME 62:333–351

    Google Scholar 

  • Klebanoff PS, Diehl FW (1951) Some features of artifically thickened fully developed turbulent boundary layers with zero pressure gradient. NACA TN 2475

  • Ligrani PM, Moffat RJ (1986) Structure of transitionally rough and fully rough turbulent boundary layers. J Fluid Mech 162:69–98

    Google Scholar 

  • Loeb GI, Laster D, Gracik T (1984) The influence of microbial fouling films on hydrodynamic drag. In: Costlow JD, Tipper R (eds) Marine biodeterioration, an interdisciplinary study. Naval Institute Press, Annapolis, Md., pp 88–94

  • Moffat R J (1988) Describing the uncertainties in experimental results. Exp Thermal Fluid Sci 1:3–17

    Article  Google Scholar 

  • Nikuradse J (1933) Laws of flow in rough pipes. NACA TM 1292

  • Perry AE, Li JD (1990) Experimental support for the attached-eddy hypothesis in zero-pressure gradient turbulent boundary layers. J Fluid Mech 218:405–438

    Google Scholar 

  • Raupach MR, Antonia RA, Rajagopalan S (1991) Rough-wall turbulent boundary layers. Appl Mech Rev 44:1–25

    Google Scholar 

  • Schlichting H (1979) Boundary-layer theory, 7th edn. McGraw-Hill, New York

  • Schoenherr KE (1932) Resistances of flat surfaces moving through a fluid. Trans SNAME 40:279–313

    Google Scholar 

  • Schultz MP (2002) The relationship between frictional resistance and roughness for surfaces smoothed by sanding. J Fluids Eng 124:492–499

    Article  Google Scholar 

  • Schultz MP, Flack KA (2003) Turbulent boundary layers over surfaces smoothed by sanding. J Fluids Eng 125: in press

    Article  Google Scholar 

  • von Kármán T (1946) On laminar and turbulent friction. NACA TM 1092

Download references

Acknowledgements

MPS would like to thank the Office of Naval Research for financial support of this research under the direction of Dr. Steve McElvaney. The authors would also like to acknowledge the ongoing financial support of the disk drag measurements from Mr. William Stoffel (NSWC-Carderock, Code 981, Shipboard R&D Office) and Dr. Alan Roberts (CNO, N420, Energy Plans & Policy). Thanks, as well, to Dr. Eric Holm, Ms. Elizabeth Haslbeck, and Ms. Jean Montemarano from NSWC-Carderock (Code 641) for allowing us to use the rotating disk facility and for providing technical guidance. Many thanks go to Mr. Steve Enzinger, Mr. Don Bunker, and the USNA Hydromechanics Laboratory and Technical Support Division staff for assisting with the project. We are also indebted to Prof. Michelle Koul for helping with the laser profilometry.

Author information

Authors and Affiliations

  1. Department of Naval Architecture and Ocean Engineering, United States Naval Academy, Annapolis, MD, 21402, USA

    M. P. Schultz & A. Myers

Authors
  1. M. P. Schultz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Myers
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. P. Schultz.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Schultz, M.P., Myers, A. Comparison of three roughness function determination methods. Exp Fluids 35, 372–379 (2003). https://doi.org/10.1007/s00348-003-0686-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00348-003-0686-x

Keywords

Search

Navigation