1 Introduction

Fourier domain mode-locked (FDML) lasers produce rapidly wavelength-swept light with bandwidths of more than 100 nm at tuning rates in the range of MHz [11, 14,15,16,17, 39]. This is achieved by synchronizing the roundtrip time of the optical field in a ring laser setup with the sweep rate of a tunable Fabry–Pérot (FP) filter, acting as the wavelength tuning element. The record sweep speeds and the excellent coherence properties have dramatically improved imaging and sensing applications, especially optical coherence tomography (OCT) [1, 30]. The overall superior combination of tuning speed, imaging depth, sensitivity and axial resolution make FDML based OCT systems an interesting alternative to high-performance OCT systems, e.g. [3, 10, 19, 25, 26, 29, 38, 40].

Due to the large time-bandwidth product and the rapid time scales in optical systems in the order of fs, the analysis of the wavelength swept light in FDML lasers is a challenging task in general. Common experimental quantities of interest are the instantaneous frequency [4], the instantaneous lineshape [2, 4, 35], and the intensity trace [13, 18, 22, 23, 27, 32, 33]. Here, we focus on the intensity trace since it can be obtained by a relatively simple measurement with a photodiode and a real-time oscilloscope. We show that the intensity trace contains sufficient information to characterize the operation mode and the physical dynamics of the FDML laser, provided that sufficient analog bandwidth is available. Timing mismatches in FDML lasers can directly be observed in the intensity trace and are referred to as high-frequency fluctuations [27] since their time scale is much shorter than the sweep period.

It has been shown that the laser can operate without high-frequency fluctuations in the intensity trace in highly dispersion compensated and highly synchronized setups over a wavelength range of more than 100 nm [27]. When timing delays, caused for example by either a residual dispersion in the fiber cavity or a detuning from the ideal sweep rate, exceed a certain amount, the intensity trace suffers from high-frequency fluctuations [27, 31] which have a negative impact on the imaging quality in OCT applications. The high-frequency fluctuations can be classified as various types, such as irregular fluctuations, referred to as a modulational instability [28, 32] and the Eckhaus instability [20], periodic Turing-type formations [28, 32] and so-called holes [27, 33].

Typically, the intensity trace of FDML lasers is recorded with measurement bandwidths of less than 10 GHz [12, 13, 18, 22, 23, 36], allowing to visualize only the low-frequency part. In this work, we characterize the intensity trace of an FDML laser at the full sweep speed using a real-time oscilloscope with a total analog bandwidth of several 10 GHz, and report on the formation of characteristic intensity patterns under different operating conditions. The relatively large measurement bandwidth is essential to fully record the high-frequency fluctuations whose temporal extensions are limited by the bandwidth of the swept bandpass filter. Our results are further validated by numerical simulations which additionally make it possible to extract the spectral features of the operating modes. Interestingly, in many cases patterns are formed instead of irregular fluctuations even under the influence of strong detunings. The advantage of the method are its simplicity and the fact that variations of the optical phase are visible in the intensity trace as amplitude fluctuations.

The paper is organized as follows: first, we describe the experimental setup and the underlying simulation model. Then we present the results and a comparison of experiment and simulation. To discuss specific properties of the high-frequency fluctuations, we demonstrate the distribution of the duration of so-called holes, i.e. dips in the intensity trace, and analyze the long-term evolution of the hole-type intensity patterns.

2 Intensity pattern types in non-synchronized FDML lasers

The intensity trace of an FDML laser contains rich information about the interplay of the laser components due to the strong phase–amplitude coupling in the cavity. The extremely narrow bandpass filter introduces large losses on the optical field when the instantaneous wavelength of the optical field is offset from the central position in the spectral filter transmission window over many roundtrips. This occurs in the case of strong synchronization mismatches between the roundtrip time of the optical field and the sweep rate of the bandpass filter, caused by e.g. the fiber dispersion or a detuning from the ideal sweep rate. Typical values of the full width at half maximum (FWHM) bandwidth of the sweep filter are in the order of 100 pm (several tens of GHz). At a wavelength of 1300 nm (231 THz) and a filter bandwidth with a FWHM of 165 pm (30 GHz), an offset of 0.02 nm (15 GHz) from the peak transmission already causes a power loss of 50% when the reflected power is absorbed by an isolator. Such losses are compensated by the semiconductor optical amplifier (SOA) gain medium with a fast response time in the order of several tens of ps [31]. This interplay of frequency-shift, gain and loss over a long time scale, i.e. when this process is iterated over many roundtrips, introduces high-frequency fluctuations in the intensity trace with a large amplitude. In the following, we first discuss the experimental laser setup as well as the simulation model, and present different types of high-frequency fluctuations by systematically detuning an FDML laser from the sweep rate at which the laser operates in the ultra-stable regime [18, 27].

2.1 Experimental setup

Fig. 1
figure 1

Schematic illustration of the experimental setup

Full size image

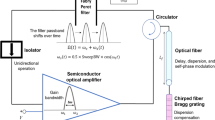
We performed measurements with two similar FDML laser setups which differ in the output power, the bandwidth of the tunable bandpass filter and the mechanism to tune the sweep frequency. The first setup is described in detail in Ref. [27]. The second setup is illustrated in Fig. 1. Here the sweep frequency of the tunable bandpass filter is kept constant, except when the laser is detuned, and the cavity length is tuned by modifying the length of a free space beam path (FSBP) to regulate the laser in the ultra-stable regime. The other components are a single polarization SOA gain medium (Thorlabs BOA1130S), a circulator (CIRC), a fiber spool consisting of a mix of SMF-28, HI1060 and LEAF fibers, and a temperature fine-tuned chirped fiber Bragg grating (cFBG) serves as a dispersion compensating element as well as the laser output (Teraxion, custom made). Further components are a polarization controller (PC) to adjust the polarization state of the light to the maximum gain axis of the SOA, a home-made tunable bandpass filter and an isolator (ISO) to ensure unidirectional lasing. The intensity trace was recorded with a 33 GHz photodiode (Discovery Semiconductors Inc. DSC20H) whose output was digitized with a 63 GHz, 160 GS real-time oscilloscope (Keysight DSOZ634A). The intensity traces referring to setup 1 are recorded with a 50 GHz photodiode.

Unless otherwise mentioned, the data presented in the manuscript refers to the first setup. The data of Sect. 4 was generated with the second setup. No qualitative differences have been observed between the two setups, and thus the results presented here do not significantly depend on details of the underlying laser setup with respect to the parameters changed in this work. Typical values for the average power at the laser output are in the first setup \({\sim 30}\, \hbox {mW}\) and in the second setup \({\sim 7}\, \hbox {mW}\). The bandwidth of the tunable bandpass filter is in the first setup 165 pm and in the second setup 290 pm, i.e. it differs by roughly a factor of 2.

2.2 Simulation model

To reproduce the experimental results, we performed simulations with the model presented in Ref. [31]. This model contains the fundamental interplay between the swept bandpass filter, a delay element such as a dispersive optical fiber or a detuning element and a single polarization SOA gain medium. The role of the simulation model in this work is twofold. First, by reproducing the measured intensity patterns, we can verify that the dynamics of the laser is sufficiently described by the three above mentioned processes, and we can identify the spectral features of the operating modes. Second, the simulation bandwidth is chosen to be 3.45 THz to show that no hidden intensity fluctuations exist which could not be captured with the limited measurement bandwidth of 33 GHz and 50 GHz, respectively.

We added the effects of carrier heating (CH) and spectral hole burning (SHB) in the SOA gain medium to the model in Ref. [31]. A quasi-static approach is used, since these processes have time constants in the order of 100 fs which is much smaller than the temporal extension of the high-frequency fluctuations in FDML lasers. Within this approach the update equation for a lumped element SOA is given by

$$\begin{aligned} u_{\text {out}}(\tau ) = \,\,&u_{\text {in}}(\tau ) \exp \left[ 0.5 h_{\text {tot}}(\tau ) \right] \nonumber \\&\cdot \exp \left\{ -{\text {i}} 0.5\left[ \alpha _{\text {N}} h_{\text {N}}(\tau ) +\alpha _{\text {CH}} h_{\text {CH}}(\tau ) \right] \right\} , \end{aligned}$$
(1)

where \(u_{\text {in,out}}\) are the slowly varying complex electric field envelopes in the swept filter reference frame [12] at the spatial input and output of the SOA, respectively. The retarded time is denoted by \(\tau\) and \(\alpha _{\text {N,CH}}\) are the linewidth enhancement factors due to band-filling and carrier heating. The total gain is given by \(h_{\text {tot}} = h_{\text {N}} + h_{\text {CH}} + h_{\text {SHB}}\) with the contributions due to band-filling \((h_{\text {N}})\), CH \((h_{\text {CH}})\) and SHB \((h_{\text {SHB}})\). The linewidth enhancement factor due to SHB \(\alpha _{\text {SHB}}\) is set to zero as in Refs. [24, 37, 41]. A description of the related differential equations of the three parts of the total gain is given in Ref. [5]. By setting \(\partial h_{{\text {CH}}}(\tau ) / \partial \tau = \partial h_{{\text {SHB}}}(\tau ) / \partial \tau \approx 0\), one can solve the resulting implicit equation with the principal branch of the Lambert W function \(W_0\) [6] by defining a nonlinear gain \(h_{\text {NL}} = h_{\text {CH}} + h_{\text {SHB}}\), and one obtains

$$\begin{aligned} h_{{\text {NL}}} (\tau ) = \,\,&\epsilon P_{{\text {in}}}(\tau ) - \tau _{\text {SHB}} \left[ \partial h_{{\text {N}}}(\tau ) / \partial \tau \right] \nonumber \\&- W_0\Big ( \Big . \epsilon P_{{\text {in}}}(\tau ) \exp \left\{ \right. \epsilon P_{{\text {in}}}(\tau ) + h_{{\text {N}}}(\tau ) \nonumber \\&- \tau _{\text {SHB}} \left[ \partial h_{{\text {N}}}(\tau ) / \partial \tau \right] \left. \right\} \Big . \Big ). \end{aligned}$$
(2)

In Eq. (2), \(\epsilon = \epsilon _{{\text {CH}}} + \epsilon _{{\text {SHB}}}\) is the combined gain compression factor where \(\epsilon _{{\text {CH}}}\) and \(\epsilon _{\text {SHB}}\) are the gain compression factors due to CH as well as SHB, and \(P_{\text {in}} = |u_{\text {in}}|^2\) is the optical power at the spatial input of the SOA. After computing the nonlinear gain \(h_{\text {NL}}\) with Eq. (2), the individual components can then be found by

$$\begin{aligned} h_{\text {SHB}} (\tau )&= -\epsilon _{\text {SHB}} P_{\text {in}}(\tau ) \nonumber \\&\quad \cdot \left\{ \exp \left[ h_{\text {N}}(\tau ) + h_{\text {NL}}(\tau )\right] - 1 \right\} \nonumber \\&\quad - \tau _{\text {SHB}} \left[ \partial h_{\text {N}}(\tau ) / \partial \tau \right] , \end{aligned}$$
(3)
$$\begin{aligned} h_{\text {CH}} (\tau )&= -\epsilon _{\text {CH}} P_{\text {in}}(\tau ) \nonumber \\&\quad \cdot \left\{ \exp \left[ h_{\text {N}}(\tau ) + h_{\text {NL}}(\tau )\right] - 1 \right\} . \end{aligned}$$
(4)

The SOA parameters are taken from [5] and are \(\tau _c = {70}\, \hbox {ps}\), \(\alpha _{\text {N}} = 1.55\), \(\alpha _{\text {CH}} = {0.94}\), \(\epsilon _{\text {CH}} = {1.95}\, \hbox {W}^{-1}\), \(\epsilon _{\text {SHB}} = {1.17}\, \hbox {W}^{-1}\), and \(\tau _{\text {SHB}} = {120}\, \hbox {fs}\). The other parameters which are different from [31] are the dispersion coefficients of the optical fiber and the cFBG which are \(\beta _{2,3,4},\hat{\beta }_{2,3,4} = 0\) for setup 1 and 2. For setup 2 the power loss factor in the fiber spool \(\kappa _f\) is 0.33, the reflectivity of the cFBG R is 0.4, the center wavelength \(\omega _c\) is \(2\pi \cdot {230.8}\, \hbox {THz}\) \(({1300}\, \hbox {nm})\), the sweep bandwidth \(D_\omega\) is \(2\pi \cdot {17.8}\, \hbox {THz}\) \(({100}\, \hbox {nm})\), the FP filter bandwidth \(\Delta _\omega\) is \(2\pi \cdot {50.7}\, \hbox {GHz}\) \(({0.290}\, \hbox {nm})\), the FP filter transmission \(T_{\text {max}}\) is 0.075 including the losses of the FSBP as well as the PC, and the total cavity losses L are \({20}\, \hbox {dB}\).

2.3 Detuning from the ultra-stable regime

Fig. 2
figure 2

a Measured intensity trace of a backward sweep. The laser is detuned by − 100 mHz from the ultra-stable regime. b The same case as in a but with a positive sign in the detuning. c Zoom into an arbitrary position in the sweep which demonstrates that the intensity trace contains mainly hole-type patterns when the roundtrip time of the optical field is smaller than the sweep rate. d The same as in c but for a reversed sign in the detuning, demonstrating that fringes form instead of holes. e Single hole and f single fringe

Full size image
Fig. 3
figure 3

Measured intensity trace of a backward sweep. The laser is detuned by a − 10 Hz from the ultra-stable regime and b by + 10 Hz. c Zoom into an arbitrary position to demonstrate the existence of quasi-periodic patterns instead of irregular fluctuations. d Similar to c but for reversed sign in the detuning, resulting in different shape. e, f Zoom into five patterns with similar shape

Full size image

In Fig. 2 the experimental intensity traces of a laser detuned by ± 100 mHz from the ultra-stable regime are shown at different time scales: The full sweep in Fig. 2a, b, an arbitrarily selected 40 ns window in Fig. 2c, d and individual patterns in Fig. 2e, f, respectively. The sinusoidal filter sweep rate in both cases is 411 kHz and the gain medium is operated with a 12.5% duty cycle [27], such that a single sweep lasts \({\approx ~300}\, \hbox {ns}\) where the sweep filter drive function is nearly linear. The sweep in this time window has a bandwidth of 117 nm and is centered at a wavelength of 1292 nm. Interestingly, the density of high-frequency fluctuations is similar in both cases in Fig. 2a, b, yet the shape of the emerging patterns is different. We collected a large number of measurements by systematically detuning the laser from the sweep rate in the ultra-stable regime and conclude that

  • moderate negative detuning of a backward sweep is dominated by holes, see Fig. 2a, c, e, whereas

  • moderate positive detuning of a backward sweep is dominated by localized fringes, see Fig. 2b, d, f.

  • In the case of a forward sweep the situation is reversed, i.e. holes occur at + 100 mHz and fringes at − 100 mHz, respectively.

  • At strong detunings, short quasi-periodic patterns can occur at certain positions in the sweep with different shape in the backward and forward sweep, as discussed below.

These patterns are a result of the long-term interplay of the swept bandpass filter, the SOA gain medium and the frequency shift per roundtrip caused by the detuning, as will be shown in Sect. 3. The qualitative shape of the patterns does not depend on the temporal position in the sweep.

Figure 3 presents a comparison to the same setup as above, however for strong detuning of ± 10 Hz. As can be seen in Fig. 3c, d, a pulsed output is generated rather than irregular fluctuations, which might be unexpected when looking at the full sweeps in Fig. 3a, b. Yet, only short quasi-periodic groupings of pattern happen, and in some parts of the intensity trace irregular fluctuations can occur. Therefore, a solitary solution does not exist in this particular setup. From a fundamental point of view, it is interesting if a periodic pulsed solution in FDML lasers can exist at all and if such a solution constitutes a new type of dissipative soliton [9].

3 Comparison to the simulation model

Fig. 4
figure 4

a Simulated intensity trace of a laser which is detuned by − 100 mHz as in Fig. 2. b The same case as in a but with a different sign in the detuning. c Zoom into an arbitrary position in the sweep. d The same as in c but for reversed sign in the detuning, resulting in fringes instead of holes. e Extraction of a single hole and f of single fringes

Full size image
Fig. 5
figure 5

Simulated intensity trace of a laser which is detuned by a − 10 Hz and b by + 10 Hz as in Fig. 3. c Zoom into a similar position as in the experimental case to demonstrate the existence of short-term quasi-periodic patterns instead of irregular fluctuations. d Similar to c but for reversed sign in the detuning, resulting in different shape. e, f Zoom into five patterns with similar shape

Full size image

We performed numerical simulations of the first setup to reproduce Figs. 2 and 3. Here we neglected the dispersion in the fiber spool causing a maximum residual group delay of less than 200 fs [27], since this contribution is small compared to the delay introduced by a detuning of ± 100 mHz (± 10 Hz) per roundtrip which is \({ \sim 590}\, \hbox {fs}\) (\({\sim 5.9}\, \hbox {ps}\)) in the case of a linear sweep. Yet, differences in the hole density due to the unknown residual dispersion as well as residual temperature fluctuations in the experiment are to be expected, especially in the case of low detuning.

As can be seen from Figs. 4 and 5, the simulation model reproduces the qualitative behavior of the experimental data in Sect. 2.3 extremely well and is therefore an excellent tool to study the FDML laser dynamics. Yet, differences in the exact shape exist in the case of the local fringes or the quasi-periodic patterns while holes can be reproduced almost exactly, see also [31]. This observation shows that the accuracy of the individual spectral shifts introduced by the SOA, the bandpass filter or the detuning are a bottleneck in modeling FDML lasers, which has not yet been fully addressed in literature in this detail, to the best of our knowledge.

In Fig. 4d, f, the local fringes are reduced in length, and thus also the density differs by roughly a factor of three. For negative detuning, the quasi-periodic patterns have a similar shape as in experiment (see Fig. 3e), but a higher periodicity in Fig. 5e. We found that individual shapes can indeed be reproduced by modifying the SOA parameters. In the case of Fig. 5e a higher \(\alpha _{\text {N}}\) of around 3 qualitatively destabilizes the strong periodicity, yielding a good match of the detailed shape with the experimental result in Fig. 3e. The local fringes in Fig. 4f and the pattern in Fig. 5f agree well with experiment for \(\tau _c = {380}\, \hbox {ps}\) and \(\alpha _N = {5.0}\), but at the cost of a worse agreement in terms of the hole duration statistics, as will be discussed in Sect. 4. Generally speaking, the assumption of a static carrier lifetime \(\tau _{\text {c}}\) and linewidth enhancement factor \(\alpha _{\text {N}}\) limits the accuracy of the model [31, 37, 41], but as presented in this work it is still an ideal tool to predict and study the dynamical processes of FDML lasers from a qualitative point of view. As can be speculated from the previous discussion, an optimal set of time independent SOA parameters exists with the best match to the experimental intensity pattern in the sense of e.g. an Euclidean distance [21]. Yet, due to the nonstationary nature of the intensity patterns, the development of a suitable cost function is a challenging task and from a physical point of view this approach is questionable anyway. Therefore, such a procedure is not followed in this work.

A considerable dependence of the pattern shapes on the gain compression parameters \(\alpha _{\text {CH}}\), \(\epsilon _{\text {CH,SHB}}\) or \(\tau _{\text {SHB}}\) could not be observed. In particular, the contribution of the last term in Eqs. (2) and (3) involving \(\tau _{\text {SHB}}\) is two orders of magnitude smaller than \(h_{\text {SHB}}\) and \(h_{\text {CH}}\). The dominant component of the total gain is the band-filling component \(h_{\text {N}}\), and the CH and SHB components add a perturbation to \(h_{\text {N}}\). According to Eq. (1), the intensity of the incoming field is modified by the gain compression terms according to \(\exp \left[ h_{\text {NL}} (\tau )\right]\), and the instantaneous frequency according to \((1/4/\pi )\alpha _{\text {CH}} \partial h_{\text {CH}}(\tau ) / \partial \tau\). Note that a change in the instantaneous frequency of the optical field affects the intensity in subsequent roundtrips because of the frequency dependent loss induced by the bandpass filter. This effect is best observed in the hole duration statistics discussed in Sect. 4. The ratio \(\exp \left[ h_{\text {NL}} (\tau )\right] / \exp \left[ h_{\text {tot}} (\tau )\right]\), computed from the individual gain terms stored in the simulation, yields the change in the intensity due to the gain compression terms. According to our simulation results, this change is in the range of 1–7% for various sweeps and detunings. As observed by a visual comparison of the patterns of simulations with and without the CH and SHB terms, the shape of the presented patterns is not changed considerably by this modification, and for example in the case of the hole-type patterns, this difference can hardly be captured on a visual basis. Therefore, we refer to the hole duration statistics in Sect. 4 for a discussion of the long-term effect.

3.1 Spectral signatures of the optical field related to the formation of intensity patterns

In the subsequent discussion, we address the spectral dynamics related to the formation of different patterns, such as holes or fringes in Figs. 2 and 4, with respect to the sign of the detuning from the ultra-stable regime.

Fig. 6
figure 6

a, b Mean frequency of the instantaneous lineshape for different strengths of a negative and b positive detunings. c, d Instantaneous lineshape at the spatial input and output position of the swept FP filter at the marked position c in the forward and d in the backward sweep in a. The sweep filter transmission window is added in yellow for comparison in c, d

Full size image

The formation of different patterns can be associated with different positions of the instantaneous lineshape in the spectral transmission window of the tunable bandpass filter. The instantaneous lineshape is defined and computed as in Ref. [31], and this approach has also been used to reproduce measured lineshapes [34, 35]. The lineshape was averaged over 25 roundtrips to reduce spectral fluctuations. In Fig. 6a, b the mean frequency of the instantaneous lineshape (MFL), or similarly the center of gravity, at the \({40,000}^{\mathrm{th}}\) roundtrip is plotted for both sweep directions and for different signs as well as strengths in detuning. This procedure is iterated at the spatial input and output of the swept FP filter. Note that the results refer to the field in the swept filter reference frame and the linewidth is not broadened by the sweep filter movement [35]. Clearly, each operating regime is associated with either a different position of the mean frequency with respect to the center of the swept bandpass filter, here at 0 GHz, or a more pronounced spectral shift of the lineshape as in the case of the backward sweep in Fig. 6a or forward sweep in Fig. 6b, respectively. To exemplarily illustrate the spectral shift of the lineshape by the FP filter, the transformation of the lineshape at the marked positions in Fig. 6a for ± 10 Hz is shown in Fig. 6c, d. The simulation also confirms that the sign of the detuning simply interchanges the position of the mean frequency in the forward and backward sweep and therefore the type of pattern which dominates the intensity trace.

Furthermore, the position of the MFL with respect to the center of the transmission window of the swept bandpass filter is consistent with the sign of the frequency shift \(\delta f\) caused by the detuning per roundtrip in the instantaneous frequency of the optical field. This frequency shift can approximately be computed by \(\delta f = \tau _{\text {d}}\, \partial \omega _s(\tau ) / \partial \tau\) [31]. Here \(\tau _{\text {d}}\) is the temporal delay of the optical field with respect to the center frequency of the swept bandpass filter, caused by a detuning from the filter sweep rate \(f_0\) by the frequency \(f_{\text {d}}\). The center frequency of the swept bandpass filter is \(\omega _s(\tau ) + \omega _c\) with the center frequency of the sweep \(\omega _c\) and \(\omega _s(\tau + 1/f_0) = \omega _s(\tau )\). In our setup the relative sweep frequency \(\omega _s\) is nearly linear in the time window where the gain medium is switched on, i.e. \(\partial \omega _s / \partial \tau \approx \pm m D_\omega /T\) with \(m=1/{12.5}\%=8\) to account for the modulation of the gain medium. In the backward sweep \(\partial \omega _s / \partial \tau > 0\) and in the forward sweep \(\partial \omega _s / \partial \tau < 0\) respectively. Note that the terminus forward or backward refers to the change in wavelength. Thus, the modified roundtrip time is \(T + t_{\text {d}}= 1/(f_0 + f_{\text {d}})\) in the detuned case. The delay \(\tau _{\text {d}}\) is then given by \(-f_{\text {d}}T^2/(1 + f_{\text {d}}T) \approx -f_{\text {d}}T^2\) [12], since \(|f_{\text {d}}T| \ll 1\) for typical sweep parameters. By combining the above equations we have

$$\begin{aligned} \delta f = -m \frac{f_{\text {d}}}{f_0}D_\omega \mathop {\text {sgn}}\left( \frac{\partial \omega _s}{\partial \tau }\right) \end{aligned}$$
(5)

with the signum function \(\mathop {\text {sgn}}\). We can now compute \(\delta f\) for \(\mp\) 100 mHz which is \(\mp\) 41 MHz in the case of the forward sweep and ± 41 MHz in the backward sweep case, respectively. The sign of \(\delta f\) explains the position of the MFL in Fig. 6a, b where in the case of \(\delta f > 0\) the mean frequency is located near the center of the filter but is greater than zero most of the time. Interestingly, in Ref. [7] an instable right hand side of the bandpass filter, which is in Fig. 6c, d at \(f > 0\), has been discussed in the context of SOA fiber ring lasers. Here, a combination of modulational instability and asymmetric four wave mixing between longitudinal cavity modes in the presence of the frequency dependent loss of the bandpass filter prohibits the instantaneous lineshape to stabilize at frequencies \(f > 0\). Furthermore, the position of the MFL scales with the strength of the detuning as well as the magnitude of the spectral shift introduced by the FP filter as presented in Fig. 6. Especially the formation of short quasi-periodic patterns is related to a large shift in the MFL compared to the case of localized fringes or hole patterns. The fact that the MFL is nearly constant in a single sweep agrees well with the observation in experiment that the type of pattern does not change over the full sweep.

In summary, we have shown that our simulation model reproduces the patterns in different operating modes on a qualitative basis and we discussed that the spectral position of the instantaneous lineshape in the sweep filter is strongly correlated with the type of pattern in the intensity trace. We also computed the spectral shift in the optical field introduced by the detuning and found consistent agreement between the sign of \(\delta f\) and the position of the MFL with respect to the center of the filter transmission window. In addition, the symmetry between backward and forward sweep when the sign of the detuning is changed can be confirmed by an equivalent symmetry of the MFL.

4 Statistical evaluation of the hole duration

The patterns discussed in Sect. 2 are not stationary over a long time scale and the hole-type patterns in particular appear to propagate as well as modify their shape over successive roundtrips [27]. Furthermore, they are distorted by noise, such as fluctuations induced by the amplified spontaneous emission (ASE) noise of the SOA.

In this context, it is of practical as well as fundamental interest to extract the characteristic features of the individual patterns. Furthermore, this enables a systematic comparison to numerical simulations and contributes to a better visualization of their long time behavior. In the case of holes such as in Fig. 2a, c, d, the temporal extension is an interesting fundamental parameter. Here, we describe a simple and robust algorithm to extract the hole duration from noisy data and present the distribution of the hole duration over a large number of roundtrips.

4.1 Definition of the hole duration

We define the hole duration \(\Delta t_{\text {h}}\) as \(t_2 - t_1\), where \(t_1\) is the point in time when the intensity is 75% above the minimum of the dip, and \(t_2\) is the point in time when the intensity has decreased by 75% from the maximum of the overshoot. An illustration is given in Fig. 7.

Fig. 7
figure 7

Illustration of the algorithm to calculate the hole duration. The local mean is subtracted from the intensity trace. Therefore the zero-intensity line represents the reference level. The black dashed line is the threshold level, i.e. when the minimum of the dip deviates by more than 50% from the local mean

Full size image

The magnitudes of the overshoots as well as the dips are measured from the local mean of the intensity trace obtained by low-pass filtering the intensity trace at 100 MHz.

The algorithm detects all local minima which deviate from the local mean by at least 50% and have a minimum distance of 40 ps to neighboring peaks. Starting from each detected dip, it identifies the point \(t_1\) by moving backwards in time until the intensity has increased by 75% from the minimum of the dip. The point \(t_2\) is found by moving forward in time: first, the algorithm moves from the dip to the intersection with the local mean and the intensity trace. Starting from this point the overshoot is tracked until the next intersection with the local mean. Based on this curve, the first local maximum is determined, and from there the algorithm moves to \(t_2\) when the intensity has decreased by 75% from the local maximum. The algorithm requires a smooth intensity trace since for optimal performance the analyzed curves should be de- or increasing monotonously in the time window of observation. Therefore, the simulated intensity trace was additionally smoothed with a Gaussian filter with a FWHM of 200 GHz to remove the impact of ASE noise. The measured intensity traces were up-sampled by a factor of ten to remove a discrete timing jitter in the hole duration caused by the finite sampling rate of the real-time oscilloscope of \({6.25}\, \hbox {ps}\) which is also the width of the bins in the histograms of the hole duration, which are presented in the subsequent section.

Fig. 8
figure 8

a, b Histograms of the hole duration in experiment of backward sweeps detuned by a − 5 Hz and b − 200 mHz, obtained from 800 consecutive roundtrips. c, d Histograms computed from simulated intensity traces of the same setup as in b with the effects of CH and SHB included in c and excluded in d

Full size image

4.2 Results

We evaluated 800 consecutive backward sweeps of the second setup, corresponding to an observation time of 2 ms. The laser was detuned by − 200 mHz as well as − 5 Hz to operate in the hole dominated regime. The center wavelength was 1300 nm and the sweep bandwidth was 100 nm. The histogram obtained from the experimental data of a laser detuned by − 5 Hz with the above discussed algorithm is shown in Fig. 8a. It can be observed that the hole duration is not a constant quantity and has an asymmetric distribution around a dominating peak which is in Fig. 8a associated with the bar in the interval [40.625 ps 46.875 ps], containing 240,406 holes which corresponds to 25.24%. A histogram produced from the same laser but detuned by − 200 mHz has almost identical relative heights as demonstrated in Fig. 8b. Hence, it can be expected that the strength of the detuning is not a crucial parameter as long as the intensity trace is hole dominated. In addition, the distribution can be expected to be stationary. The maximum peak is also in the interval [40.625 ps 46.875 ps] with 12,103 holes and the estimated probability of 25.21% is similar as before. The reproduced histogram obtained from the simulation of the same setup as in Fig. 8b is presented in Fig. 8c. The location of the peak, which is in Fig. 8c in the interval [46.875 ps 53.125 ps] with 21 860 holes (37.34%), and the asymmetric broadening can be well reproduced. The variation in the hole duration can therefore be attributed to the inherent laser dynamics, particularly the frequency-shift-gain-loss interplay.

The more pronounced spread around the peak interval in the experimental data can partly be attributed to the wavelength and carrier density dependency of the carrier lifetime \(\tau _c\) or the linewidth enhancement factor \(\alpha _{\text {N}}\), which is not included in the simulation and thus the time dependency of \(\tau _c \text{ and } \alpha _{\text {N}}\) as mentioned in Sect. 3. Furthermore, the bandwidth of the tunable bandpass filter is wavelength dependent and kept constant in the simulation. The bandwidth has been measured in the second setup and it is found to vary by 20% over most of the wavelength range. Our simulations show that the position of the peak of the histogram depends on the filter bandwidth and likely results in a broadening of the histogram when varying over the sweep. The above mentioned effects are expected to contribute to the additional broadening seen in experiment from Fig. 8a, b, yet require complex models prohibiting practical simulation times.

The percentage of detected holes which are larger than 165 ps and are thus not shown is \({<1}\%\) in the experimental as well as the simulated data sets from Fig. 8. The total number of holes is in Fig. 8a 952,330, in Fig. 8b 48,037 and in the simulation in Fig. 8c, d 50,000 were collected.

The influence of the gain compression parameters on the hole duration statistics is displayed in Fig. 8d. Here, the effects of CH and SHB are not considered in the simulation, i.e. \(\epsilon _{\text {CH,SHB}} = \alpha _{\text {CH}} = 0\). It can be seen that the asymmetry as well as the overall shape match better to experiment if the CH and SHB terms are included in the simulation. Based on these findings, it can be concluded that the nonlinearity added by CH and SHB contributes to a better agreement in the asymmetric broadening discussed above. All in all, a comparison to experimental results heavily relies on an accurate modeling of the frequency-shift-gain-loss interplay, and the hole duration statistics can serve as a tool to assess complex processes.

The histogram of the hole duration presented above gives a valuable insight in the dynamical quantities of FDML lasers and can also be used to quantify simulation models and their accuracy. The key in this context is that the sign and the sweep direction determine the shape of the intensity patterns and one can control if the intensity trace is dominated by hole formation up to an upper bound when the detuning becomes too large, as shown in Fig. 3. Our results are at least valid for the presented sweep parameters in this work. In other setups with an extremely narrow bandwidth of the bandpass filter of 8.75 GHz it has been shown that also modified hole-type patterns can occur near the lasing threshold [8].

The distribution of the hole duration is also of fundamental interest since the SOA gain medium with its complex microscopic dynamics has a significant impact on the shape of the intensity patterns, as discussed above. Therefore, a qualitative agreement of experimental and simulation data is a necessary condition for the simulation model to be accurate.

5 Conclusion

We presented various intensity pattern types in rapidly swept FDML lasers and identified their operating conditions. By detuning the laser from the sweep rate at which the laser operates in the ultra-stable regime, the sign as well as the magnitude of the detuning and the sweep direction determine if the intensity trace of the laser is dominated by holes, localized fringes or short-term quasi-periodic groupings of pulsed patterns. Our experimental results are consistent with numerical simulations, showing that the formation of patterns is a result of the frequency-shift-gain-loss interplay in the laser cavity over a long time scale. By controlling the shape of the patterns, we were able to extract the distribution of the hole duration, giving insight in the dynamical quantities of the complex dynamics in FDML lasers.