1 Introduction

Van der Waals or Casimir interaction between neutral but polarizable atoms (or molecules) is the dispersion interaction caused by quantum fluctuations of the electromagnetic field that spontaneously induce a polarization in matter [1,2,3,4]. The resulting dipole–dipole interaction leads to a typically attractive potential that quickly decays for increasing distance between the dipoles. A large number of studies have been carried out for the dispersion interaction between two atoms in a bulk medium [1,2,3,4], the dispersion interaction of a single atom with a macroscopic body [2, 4], and the effects of macroscopic external boundaries on two-body dispersion potentials [5,6,7,8,9]. The dispersion interaction of highly excited (Rydberg) atoms has also been investigated [9,10,11].

The dispersion potentials of atoms on the axis of a metallic or dielectric waveguide have been studied [12,13,14,15]. It has been shown that the dispersion potential of a single atom on the axis of a hollow metallic waveguide is strongly enhanced at certain resonant radii [12], the dispersion interaction between two atoms on the axis of a hollow metallic waveguide or a dielectric waveguide decays exponentially with distance [13, 15], and the dispersion potential between two atoms with axial dipoles on the axis of a dielectric waveguide is significantly enhanced [14, 15].

The dispersion interaction between atoms located off axis inside or outside a waveguide has also been investigated [16]. It has been shown that moving the atoms off axis can drastically reduce the dispersion interaction energy in the case of axial and azimuthal dipoles and can convert suppression of the dispersion interaction into enhancement in the case of radial dipoles.

The enhancement or reduction of the dispersion interaction energy due to a material object is usually characterized by the ratio between the dispersion interaction energy in the presence of the object and the corresponding dispersion interaction energy in free space. In the previous studies [12,13,14,15,16], the dispersion interaction between atoms with the same dipole orientations has been considered. For such atoms, the dispersion interaction in free space is nonzero and the enhancement factor due to the presence of a waveguide is a finite quantity.

The aim of this paper is to study the waveguide-induced dispersion interaction between two atoms with dipoles orthogonal to each other and to the interatomic axis. For such atoms, the dispersion interaction is zero in free space but may be not zero in the presence of a cylindrical waveguide, leading to an infinitely large enhancement factor. This waveguide-induced dispersion interaction appears as a consequence of the anisotropy of the surrounding medium of the atoms.

The paper is organized as follows. In Sect. 2, we describe the model system and present the basic equations. In Sect. 3, we present the results of numerical calculations. Our conclusions are given in Sect. 4.

2 Model and interatomic dispersion interaction

In this section, we describe the model and present the basic equations for the waveguide-modified dispersion interaction potential between ground-state two-level atoms.

2.1 Model and basic equations

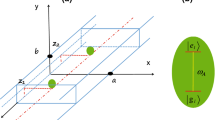
We consider two two-level atoms placed outside a cylindrical vacuum-clad waveguide (see Fig. 1). We label the atoms by the indices \(j=1,2\). Each atom has an upper energy level \(|+\rangle _j\) and a lower energy level \(|-\rangle _j\). We assume that the electric-dipole transition between these two levels is allowed. The transition frequency and the dipole matrix element of atom j are denoted by the symbols \(\omega _j\) and \({\mathbf {d}}_j\), respectively. The vacuum-clad waveguide is a dielectric or metallic cylinder of radius a and dielectric constant \(\epsilon _1\) and is surrounded by an infinite background vacuum or air medium of dielectric constant \(\epsilon _2=1\). We use Cartesian coordinates \(\{x,y,z\}\), where z is the coordinate along the waveguide axis, and also cylindrical coordinates \(\{r,\varphi ,z\}\), where r and \(\varphi\) are the polar coordinates in the fiber transverse plane xy. The position vectors of the atoms are denoted by the symbols \({\mathbf {R}}_j\).

Fig. 1
figure 1

Two two-level atoms near a cylindrical vacuum-clad waveguide

Full size image

We assume that the atoms are in their ground states. The interatomic dispersion potential has been obtained from the mutually induced dipole–dipole interaction within fourth-order perturbation theory [4, 6]. The expression for the dispersion potential between the ground-state atoms is [4, 6]

$$\begin{aligned} U_{12}({\mathbf {R}}_1,{\mathbf {R}}_2)= & {} -\frac{2\mu _0^2}{\pi \hbar }\omega _1\omega _2 \int _{0}^{\infty }\mathrm{d}u\frac{u^4}{(\omega _1^2+u^2)(\omega _2^2+u^2)}\nonumber \\&\times |{\mathbf {d}}_1\cdot {\mathbf {G}}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)\cdot {\mathbf {d}}_2^*|^2, \end{aligned}$$
(1)

where \({\mathbf {G}}({\mathbf {R}}_1,{\mathbf {R}}_2;\omega )\) is the electric Green tensor of the waveguide for the field with a frequency \(\omega\) and iu is the imaginary frequency. We note that \({\mathbf {G}}({\mathbf {R}}_1,{\mathbf {R}}_2;\omega )\) depends on the dielectric constant \(\epsilon _1(\omega )\) of the waveguide. Consequently, the Green tensor \({\mathbf {G}}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)\) at the imaginary frequency iu depends on \(\epsilon _1(iu)\). We also note that \(U_{12}\le 0\) and \(U_{12}({\mathbf {R}}_1,{\mathbf {R}}_2)=U_{21}({\mathbf {R}}_2,{\mathbf {R}}_1)\).

For the outer space of the waveguide (\(R_1,R_2>a\)), the Green tensor \({\mathbf {G}}\) can be presented as

$$\begin{aligned} {\mathbf {G}}={\mathbf {G}}^{(0)}+{\mathbf {G}}^{({\mathrm {sc}})}, \end{aligned}$$
(2)

where \({\mathbf {G}}^{(0)}\) and \({\mathbf {G}}^{({\mathrm {sc}})}\) are the vacuum and scattering parts, respectively. The expression for the vacuum Green tensor \({\mathbf {G}}^{(0)}\) is given as [4, 17]

$$\begin{aligned}&{\mathbf {G}}^{(0)}({\mathbf {R}}_1,{\mathbf {R}}_2,\omega )= -\frac{1}{3k^2}\delta ({\mathbf {R}}_2-{\mathbf {R}}_1){\mathbf {I}}\nonumber \\&\quad +\frac{\exp (ikR)}{4\pi R}\left[ \left( 1+\frac{ikR-1}{k^2R^2}\right) {\mathbf {I}} \right. \nonumber \\&\quad +\left. \frac{3-3ikR-k^2R^2}{k^2R^2}\hat{{\mathbf {R}}}\otimes \hat{{\mathbf {R}}}\right] , \end{aligned}$$
(3)

where \(k=\omega /c\) is the wave number and the notations \(R=|{\mathbf {R}}|\) and \(\hat{{\mathbf {R}}}={\mathbf {R}}/R\) with \({\mathbf {R}}={\mathbf {R}}_2-{\mathbf {R}}_1\) have been introduced. The expression for the scattering Green tensor \({\mathbf {G}}^{({\mathrm {sc}})}\) is given in Refs. [18,19,20,21].

The equality \(|{\mathbf {d}}_1\cdot {\mathbf {G}}\cdot {\mathbf {d}}_2^*|^2=|{\mathbf {d}}_1\cdot {\mathbf {G}}^{(0)}\cdot {\mathbf {d}}_2^*|^2+|{\mathbf {d}}_1\cdot {\mathbf {G}}^{({\mathrm {sc}})}\cdot {\mathbf {d}}_2^*|^2+2{\mathrm {Re}}[({\mathbf {d}}_1\cdot {\mathbf {G}}^{(0)}\cdot {\mathbf {d}}_2^*)({\mathbf {d}}_1^*\cdot {\mathbf {G}}^{({\mathrm {sc}})*}\cdot {\mathbf {d}}_2)]\) leads to the decomposition of the dispersion potential \(U_{12}\) into three terms, \(U_{12}=U_{12}^{(0)}+U_{12}^{({\mathrm {sc}})}+U_{12}^{({\mathrm {cross}})}\), which have clear physical meanings [15]. The first term, \(U_{12}^{(0)}\), results from loops of two freely propagating photons. It dominates in the near-field region of distances \(R\equiv |{\mathbf {R}}_2-{\mathbf {R}}_1|\ll \lambda _j\) (with \(\lambda _j\equiv 2\pi c/\omega _j\) and \(j=1,2\)) and scales as \(R^{-6}\) in this region. The second term, \(U_{12}^{({\mathrm {sc}})}\), is due to loops of two scattered photons. At short distances, it tends to a constant value [15]. The third term, \(U_{12}^{({\mathrm {cross}})}\), consists of loops involving a single-scattered photon and a single freely propagating photon. It has a subleading \(R^{-3}\) scaling at short distances [15].

2.2 Dispersion interaction between two two-level atoms in free space

In the case where the atoms are in free space, we have \({\mathbf {G}}={\mathbf {G}}^{(0)}\). With the help of Eqs. (1) and (3), we obtain, for \({\mathbf {R}}_1\not ={\mathbf {R}}_2\), the following expression for the vacuum dispersion interaction potential [4, 6]:

$$\begin{aligned} U_{12}^{(0)}({\mathbf {R}}_1,{\mathbf {R}}_2)= & {} -\frac{\mu _0^2\omega _1\omega _2}{8\pi ^3\hbar R^2}\int _{0}^{\infty }\mathrm{d}u\frac{u^4e^{-2uR/c}}{(\omega _1^2+u^2)(\omega _2^2+u^2)}\nonumber \\&\times \left| \left( 1+\frac{1}{uR/c}+\frac{1}{u^2R^2/c^2}\right) {\mathbf {d}}_1\cdot {\mathbf {d}}_2^*\right. \nonumber \\&-\left. \left( 1+\frac{3}{uR/c}+\frac{3}{u^2R^2/c^2}\right) ({\mathbf {d}}_1 \cdot \hat{{\mathbf {R}}})({\mathbf {d}}_2^*\cdot \hat{{\mathbf {R}}})\right| ^2. \end{aligned}$$
(4)

In the nonretarded limit, where \(R\ll 2\pi c/\omega _1,2\pi c/\omega _2\), the integral in Eq. (4) is effectively limited to the region \(uR/c\ll 1\). Then, we have \(e^{-2uR/c}\simeq 1\). In addition, the dominant terms in the vertical bars in Eq. (4) are associated with the factor \(1/(u^2R^2/c^2)\). Hence, we obtain

$$\begin{aligned} U_{12}^{(0)}({\mathbf {R}}_1,{\mathbf {R}}_2)=-\frac{C_6}{R^6}, \end{aligned}$$
(5)

where

$$\begin{aligned} C_6=\frac{1}{16\pi ^2\hbar \epsilon _0^2(\omega _1+\omega _2)} |{\mathbf {d}}_1\cdot {\mathbf {d}}_2^*-3({\mathbf {d}}_1 \cdot \hat{{\mathbf {R}}})({\mathbf {d}}_2^*\cdot \hat{{\mathbf {R}}})|^2. \end{aligned}$$
(6)

In the retarded limit, where \(R\gg 2\pi c/\omega _1,2\pi c/\omega _2\), only small values \(u\ll \omega _1,\omega _2\) contribute to the integral in Eq. (4). In this case, we can drop \(u^2\) in the factors \(\omega _1^2+u^2\) and \(\omega _2^2+u^2\) in the denominator of the integrand. Then, we obtain

$$\begin{aligned} U_{12}^{(0)}({\mathbf {R}}_1,{\mathbf {R}}_2)=-\frac{C_7}{R^7}, \end{aligned}$$
(7)

where

$$\begin{aligned} C_7= & {} \frac{c}{32\pi ^3\hbar \epsilon _0^2\omega _1\omega _2}\{13|{\mathbf {d}}_1\cdot {\mathbf {d}}_2^*|^2+63|{\mathbf {d}}_1 \cdot \hat{{\mathbf {R}}}|^2 |{\mathbf {d}}_2^*\cdot \hat{{\mathbf {R}}}|^2\nonumber \\&-56\,{\mathrm {Re}}[({\mathbf {d}}_1^*\cdot {\mathbf {d}}_2) ({\mathbf {d}}_1 \cdot \hat{{\mathbf {R}}}) ({\mathbf {d}}_2^*\cdot \hat{{\mathbf {R}}})]\}. \end{aligned}$$
(8)

It is interesting to note that, in the case where the dipole matrix-element vectors \(\mathbf {d}_1\) and \(\mathbf {d}_2\) are perpendicular to each other and to the interatomic axis, that is,

$$\begin{aligned} {\mathbf {d}}_1\perp & {} {\mathbf {d}}_2\nonumber \\ {\text{ and } \text{ either }}\quad {\mathbf {d}}_1\perp & {} {\mathbf {R}} {\text{ or }}\quad {\mathbf {d}}_2\perp {\mathbf {R}}, \end{aligned}$$
(9)

we have \(U_{12}^{(0)}=0\).

When the dipole is oriented randomly in space, we can take the average of the expression in the integrand of Eq. (4) over the orientation directions of the vectors \({\mathbf {d}}_1\) and \({\mathbf {d}}_2\). Then, we obtain the dipole-orientation-averaged vacuum dispersion potential [6]

$$\begin{aligned}\bar{U}_{12}^{(0)}({\mathbf {R}}_1, {\mathbf {R}}_2) & = -\frac{\omega _1\omega _2|d_1|^2|d_2|^2 }{36\pi ^3\hbar \epsilon _0^2 R^6} \int _{0}^{\infty }\mathrm{d}u\frac{e^{-2uR/c}}{(\omega _1^2+u^2)(\omega _2^2+u^2)} \nonumber \\&\quad \times [(uR/c)^4+2(uR/c)^3+5(uR/c)^2+6uR/c+3]. \end{aligned}$$
(10)

The corresponding average values of the coefficients \(C_6\) and \(C_7\) are found to be [6] \(\bar{C}_6=|d_1|^2|d_2|^2/[24\pi ^2\hbar \epsilon _0^2(\omega _1+\omega _2)]\) and \(\bar{C}_7={23c|d_1|^2|d_2|^2}/[{144\pi ^3\hbar \epsilon _0^2\omega _1\omega _2}]\).

2.3 Waveguide-induced dispersion interaction between two atoms with orthogonal in-transverse-plane dipoles

In the presence of the waveguide, under conditions (9), although \(U_{12}^{(0)}=0\), we still may have \(U_{12}\not =0\). In order to illustrate such a situation, we assume that the atoms are aligned along a line parallel to the fiber axis z. Then, without loss of generality, we can write \({\mathbf {R}}_1=(r,0,0)\) and \({\mathbf {R}}_2=(r,0,z)\) in the cylindrical coordinates. We consider the case where the atomic dipole vectors are linearly polarized in the transverse plane xy and are orthogonal to each other. In this case, we can write \({\mathbf {d}}_1=d_1(\cos \phi _1,\sin \phi _1,0)\) and \({\mathbf {d}}_2=d_2(\cos \phi _2,\sin \phi _2,0)\) in the Cartesian coordinates, where the angles \(\phi _1=\phi\) and \(\phi _2=\phi +\pi /2\) characterize the directions of the orthogonal atomic dipole vectors \({\mathbf {d}}_1\) and \({\mathbf {d}}_2\) in the transverse plane xy. This leads to \(U_{12}^{(0)}=0\) and

$$\begin{aligned}&U_{12}({\mathbf {R}}_1,{\mathbf {R}}_2)\nonumber \\&\quad = -\frac{\mu _0^2}{2\pi \hbar }\omega _1\omega _2d_1^2 d_2^2\sin ^2(2\phi )\int _{0}^{\infty }\mathrm{d}u\frac{u^4}{(\omega _1^2+u^2)(\omega _2^2+u^2)} \nonumber \\&\qquad \times |G_{rr}^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)- G_{\varphi \varphi }^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)|^2. \end{aligned}$$
(11)

In deriving Eq. (11), we have used the fact that for \((r_1,\varphi _1)=(r_2,\varphi _2)\), one has the relations \(G_{r\varphi }^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)=G_{\varphi r}^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)=0\).

Due to the presence of the waveguide, the isotropy of the medium around the fiber is broken and, hence, we have \(G_{rr}^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)\not =G_{\varphi \varphi }^{({\mathrm {sc}})}({\mathbf {R}}_1,{\mathbf {R}}_2;iu)\). It is then clear from Eq. (11) that we have \(U_{12}\not =0\) when \(\phi \not = 0,\pm \pi /2,\pm \pi\). Thus, we may obtain \(U_{12}\not =0\) even when \(U_{12}^{(0)}=0\). Note that the absolute value \(|U_{12}|\) of the waveguide-mediated dispersion potential \(U_{12}\) achieves its maximal value when \(\phi =\pm \pi /4,\pm 3\pi /4\).

The reciprocity property of the Green tensor means that \({\mathbf {G}}({\mathbf {R}}_1,{\mathbf {R}}_2)={\mathbf {G}}^{{\mathrm {T}}} ({\mathbf {R}}_2,{\mathbf {R}}_1)\), where \({\mathrm {T}}\) is the transpose operation. When we use this property and Eq. (11), we find that the dispersion potential \(U_{12}\) for the considered two atoms is symmetric with respect to the interatomic distance \(z\equiv z_2-z_1\), that is, \(U_{12}(z)=U_{12}(-z)\).

Similar results can be obtained in the case where the atomic dipole vectors are oppositely circularly polarized in the transverse plane xy, that is, \({\mathbf {d}}_1=(d_1/\sqrt{2})(1,i,0)\) and \({\mathbf {d}}_2=(d_2/\sqrt{2})(1,-i,0)\) in the Cartesian coordinates. In this case, we also have \(U_{12}^{(0)}=0\) and \(U_{12}\not =0\). The expression for \(U_{12}\) is given by Eq. (11) with the replacement of the factor \(\sin ^2(2\phi )\) by 1.

3 Numerical results

In this section, we present the results of numerical calculations for the waveguide-mediated dispersion potential \(U_{12}\). In our numerical calculations, we assume that the atoms have the same transition frequencies and the same dipole magnitudes, that is, \(\omega _1=\omega _2\equiv \omega _0\) and \(d_1=d_2\equiv d\). We use the transition wavelength \(\lambda _0=2\pi c/\omega _0=852\) nm and the natural linewidth \(\gamma _0/2\pi =5.2\) MHz, which correspond to the transitions in the \(D_2\) line of \(^{133}\)Cs atoms. The atomic dipole matrix element d is calculated from the formula \(\gamma _0=d^2\omega _0^3/3\pi \epsilon _0\hbar c^3\) for the natural linewidth of a two-level atom.

Fig. 2
figure 2

Normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the separation distance \(z=z_2-z_1\) between the atoms near a vacuum-clad silica-core nanofiber. The fiber radius is \(a=250\) nm. The atoms are located on a straight line parallel to the fiber axis z at the positions \({\mathbf {R}}_1=(r,0,0)\) and \({\mathbf {R}}_2=(r,0,z)\) with \(r/a=1.2\) (solid red line), 1.4 (dashed green line), 1.6 (dash-dotted blue line), and 1.8 (dotted magenta line) in the cylindrical coordinates. The dipole matrix-element vectors of the emitters are \({\mathbf {d}}_1=(d/\sqrt{2})(1,1,0)\) and \({\mathbf {d}}_2=(d/\sqrt{2})(1,-1,0)\) in the Cartesian coordinates. The dipole magnitude \(d=|{\mathbf {d}}_1|=|{\mathbf {d}}_2|\) corresponds to the natural linewidth \(\gamma _0/2\pi =5.2\) MHz of the \(D_2\) line of a \(^{133}\)Cs atom with the transition wavelength \(\lambda _0=852\) nm. Due to the symmetry of \(U_{12}\) with respect to z, we plot it only for \(z>0\)

Full size image

It is clear that the interatomic dispersion potential \(U_{12}\) depends on the separation distance between the atoms and the distance from the atoms to the fiber. We plot in Fig. 2 the normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the atomic separation distance \(z=z_2-z_1\) between the atoms near a vacuum-clad silica-core nanofiber. The dynamical dielectric constant \(\epsilon _1\) for the silica core is calculated from the three-term Sellmeier formula [22]. The atoms are positioned on a straight line parallel to the fiber axis z at the positions \({\mathbf {R}}_1=(r,0,0)\) and \({\mathbf {R}}_2=(r,0,z)\) in the cylindrical coordinates, with \(r/a=1.2\), 1.4, 1.6, and 1.8. The dipole matrix-element vectors of the atoms are \({\mathbf {d}}_1=(d/\sqrt{2})(1,1,0)\) and \({\mathbf {d}}_2=(d/\sqrt{2})(1,-1,0)\) in the Cartesian coordinates. In this case, conditions (9) are satisfied and, hence, the vacuum dispersion potential \(U_{12}^{(0)}\) vanishes. Despite this fact, we observe from Fig. 2 that, in general, the dispersion potential \(U_{12}\) is not vanishing. We observe that \(|U_{12}|\) is very small compared to the natural linewidth \(\hbar \gamma _0\). However, the fiber-induced-modification factor \(U_{12}/U_{12}^{(0)}\) is infinitely large because \(U_{12}^{(0)}\)=0. We will show later (see Fig. 5) that, when the atoms are close enough to the surface and the separation distance between the atoms is large enough as compared to the atomic transition wavelength, the waveguide-mediated dispersion potential \(U_{12}\) can become not only comparable to but also slightly larger than the dipole-orientation-averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\).

In addition, we observe from Fig. 2 that the absolute value \(|U_{12}|\) has a dip and a peak in the dependence on the interatomic axial distance. The formation of the dip and the peak is a result of the effects of the scattering of virtual photons from the fiber surface. The positions of the dip and the peak depend on the distance from the atoms to the fiber surface. Note that, in the case of Fig. 2, the dispersion potential \(U_{12}\) tends to a finite value when the atomic separation distance z tends to 0. This feature is a consequence of the fact that, since \(U_{12}^{(0)}=0\), we have \(U_{12}=U_{12}^{({\mathrm {sc}})}\), where \(U_{12}^{({\mathrm {sc}})}\) is a function that approaches a constant value at short distances [15].

We note that in Fig. 2 we plotted the potential \(U_{12}\) only for \(z\equiv z_2-z_1>0\). The reason is that, in the case of this figure, the potential is symmetric with z. This symmetry means that direction-dependent effects [23,24,25,26,27,28] are not witnessed in the behavior of the calculated dispersion potential.

Fig. 3
figure 3

Normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the distance \(r=r_1=r_2\) from the atoms to the fiber axis. The atoms are positioned on a straight line parallel to the fiber axis with the axial separation distance \(k_0z=0.5\), 1, and 2. Other parameters are as in Fig. 2

Full size image

We plot in Fig. 3 the normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the distance \(r=r_1=r_2\) from the atoms to the fiber axis. The atoms are positioned on a straight line parallel to the fiber axis, and the separation distance between the atoms along the fiber axis is \(k_0z=0.5\), 1, and 2. Figure 3 shows that the behavior of the radial dependence of the potential \(U_{12}\) depends on the interatomic axial distance z.

Fig. 4
figure 4

Normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the dipole orientation angle \(\phi\). The atoms are positioned on a straight line parallel to the fiber axis. The axial separation distance between the atoms is \(k_0z=1\), the radial distance is \(r/a=r_1/a=r_2/a=1.4\), and the azimuthal position is \(\varphi =\varphi _1=\varphi _2=0\). The dipole matrix-element vectors of the emitters are \({\mathbf {d}}_1=d(\cos \phi ,\sin \phi ,0)\) and \({\mathbf {d}}_2=d(-\sin \phi ,\cos \phi ,0)\) in the Cartesian coordinates. Other parameters are as in Fig. 2

Full size image

The interatomic dispersion potential \(U_{12}\) depends on the directions of the atomic dipole vectors in the transverse plane xy. We plot in Fig. 4 the normalized absolute value \(|U_{12}|/\hbar \gamma _0\) of the interatomic dispersion potential as a function of the angle \(\phi\), which characterizes the orientations of the atomic dipoles relative to the radial direction. The atoms are positioned on a straight line parallel to the fiber axis. The axial separation distance between the atoms is \(k_0z=1\), the radial position is \(r/a=r_1/a=r_2/a=1.4\), and the azimuthal position is \(\varphi =\varphi _1=\varphi _2=0\). The dipole matrix-element vectors of the emitters are \({\mathbf {d}}_1=d(\cos \phi ,\sin \phi ,0)\) and \({\mathbf {d}}_2=d(-\sin \phi ,\cos \phi ,0)\) in the Cartesian coordinates. Figure 4 shows that \(U_{12}\not =0\) for \(\phi \not =0,\pi /2,\pi\). We observe that \(|U_{12}|\) achieves its maximal value when \(\phi =\pi /4,3\pi /4\).

Fig. 5
figure 5

Ratio \(U_{12}/\bar{U}_{12}^{(0)}\) between the waveguide-mediated interatomic dispersion potential \(U_{12}\) and the dipole-orientation-averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\) as a function of the separation distance \(z=z_2-z_1\) between the atoms. The inset shows the normalized absolute value \(|\bar{U}_{12}^{(0)}|/\hbar \gamma _0\) of the averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\). The parameters used are as in Fig. 2. The horizontal dotted line indicates the value 1 and is a guide to the eye. Due to the symmetry of \(U_{12}\) with respect to z, we plot only for \(z>0\)

Full size image

As already mentioned, in the case where the vacuum dispersion potential \(U_{12}^{(0)}\) is zero but the waveguide-mediated dispersion potential \(U_{12}\) is not zero, the factor \(U_{12}/U_{12}^{(0)}\) is infinitely large. In order to characterize the relative magnitude of \(U_{12}\) in this case, we can use the dipole-orientation-averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\) instead of the potential \(U_{12}^{(0)}=0\). We plot in Fig. 5 the ratio \(U_{12}/\bar{U}_{12}^{(0)}\) as a function of the separation distance \(z=z_2-z_1\) between the atoms for the parameters of Fig. 2. Comparison between the curves shows that, when the atoms are close enough to the surface and the separation distance between the atoms is large enough as compared to the atomic transition wavelength, the waveguide-mediated dispersion potential \(U_{12}\) can become not only comparable to but also slightly larger than the dipole-orientation-averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\).

Fig. 6
figure 6

Normalized absolute value \(|U_{12}|/\hbar \gamma _0\) (a) and ratio \(U_{12}/\bar{U}_{12}^{(0)}\) (b) as functions of the separation distance \(z=z_2-z_1\) between the atoms near an infinitely long cylinder made of gold (solid red lines), silicon (dashed green lines), and silica (dotted blue lines). The cylinder radius is \(a=250\) nm. The atoms are positioned on a straight line parallel to the fiber axis z at the radial position \(r/a=1.2\). Other parameters are as in Fig. 2. The horizontal dotted line in part (b) indicates the value 1 and is a guide to the eye. Due to the symmetry of \(U_{12}\) with respect to z, we plot only for \(z>0\)

Full size image

The interatomic dispersion potential \(U_{12}\) depends on the material of the waveguide. We plot in Fig. 6 the normalized absolute value \(|U_{12}|/\hbar \gamma _0\) and the ratio \(U_{12}/\bar{U}_{12}^{(0)}\) as functions of the separation distance \(z=z_2-z_1\) between the atoms near an infinitely long cylinder made of gold, silicon, and silica. The dielectric constants \(\epsilon _1\) for gold and silicon were calculated from the Drude [15, 29] and Drude–Lorentz [15, 30] models, respectively. In the case of gold, the metallic loss was taken into account by using the Drude model for the complex dielectric constant \(\epsilon _1\) of a metal [15, 29]. Figure 6 shows that the modifications caused by the gold nanowire are, in general, larger than those caused by the silicon cylinder or the silica nanofiber. Figure 6b indicates that the dispersion potential \(U_{12}\) in the cases of gold and silicon can become substantially larger than the dipole-orientation-averaged vacuum dispersion potential \(\bar{U}_{12}^{(0)}\). It is interesting to note that the two curves for gold and silicon are quite similar to each other although gold is a metal and silicon is a dielectric. This similarity is a result of the fact that the effect of the waveguide material on the potential \(U_{12}\) occurs through the dielectric constant \(\epsilon _1(iu)\), which, at the imaginary frequency \(iu\simeq i\omega _0\), takes similar real and large values for both gold and silicon in the framework of the Drude [15, 29] and Drude–Lorentz [15, 30] models, respectively. It follows from the Drude model [15, 29] that metallic losses lead to a reduction of the dielectric constant at imaginary frequency and hence to a reduction of the interatomic dispersion potential. At least for the distances we have looked at so far (\(k_0z\le 10\)), the loss in gold does not seem to manifest compared to silica or silicon at larger atomic separations when off-resonant interatomic ground-state interactions are considered—we simply see the benefit of larger potential magnitude coming from the large absolute value of the real part of gold’s permittivity.

We note that, for the parameters of Fig. 6, the dispersion potentials induced by gold, silicon, and silica waveguides are symmetric with respect to the interatomic distance \(z= z_2-z_1\), and therefore, we plotted in Fig. 6 only for \(z>0\). We could not observe any signature of unidirectional information transfer [23,24,25,26,27,28] in the obtained interatomic dispersion potential. A possible reason is that we studied atoms with dipoles aligned in the fiber transverse plane. A manifestation of chiral interaction in the dispersion potential may be observed when a dipole has both axial and radial components [31,32,33,34]. Such chiral effects can be significant in the case of metals despite the presence of losses.

4 Summary

In this paper, we have studied the dispersion interaction between two ground-state two-level atoms near a cylindrical vacuum-clad optical waveguide. We have examined the case where the electric-dipole matrix-element vectors of the atoms are perpendicular to each other and to the interatomic axis. When these atoms are in free space, the dispersion interaction between them vanishes. However, in the presence of a waveguide aligned parallel to the interatomic axis, the energy of the dispersion interaction between the atoms may become nonzero and comparable to the average energy of the dispersion interaction between two atoms with arbitrarily oriented dipoles in free space. This waveguide-induced dispersion interaction is a consequence of the anisotropy of the medium around the atoms. We have shown that the interatomic dispersion potential tends to a finite value when the atomic separation distance tends to 0. Our results are useful when trying to control and manipulate the dispersion interaction between atoms, molecules, and particles using nanofibers. Our calculations can be extended to excited atoms and to various material boundary configurations.