1 Introduction

Control of polarization state of light is vital for many industrial and scientific applications. In entertainment, stereoscopic projections and 3D movies may be watched with polarization glasses, in manufacturing quality control the material stress can be assessed via the mechanically induced birefringence and in polarized light microscopy the image contrast can be enhanced.

Most elements and devices used to manipulate light polarization are based on birefringence, dichroism or optical activity in either natural or man-made materials. New concepts are constantly explored, involving surface plasmons [1], plasmonic metasurfaces [2], or novel birefringent designs [3], and offer solutions to polarization control in a broad range of frequencies from visible up to terahertz. Among them, recent developments in three-dimensional sub-micron-resolution two-photon laser photolithography (direct laser writing) techniques [4, 5], combined with electrochemical metal deposition on a positive resist molds led to spectacular demonstration of high-aspect-ratio helical spring-like all metal structures [6]. These were verified to perform as transmission broadband circular polarizers, covering one octave in the mid-infrared between 3.2 and 6.4 μm. This concept was further developed toward more complex geometries, and the tapered helices were demonstrated with extended bandwidth and improved extinction [7]. Further theoretical (numerical) studies followed, focusing on the parameter optimization in terms of transmission, contrast and bandwidth [8,9,10]. In [11], upon comparing metal and dielectric helices, it was discovered that a trade-off exists between the transmission efficiency and bandwidth in this class of circular polarizers and other all-dielectric structures with interesting polarizing properties have also been demonstrated [12,13,14,15,16].

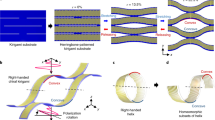
In cholesteric (also known as chiral nematic) liquid crystals, molecules tend to organize in layers with the director axis twisted by a certain angle between consecutive layers. The resulting mesoscopic helical structure has some unique optical properties; among them is the structural coloration that has already found practical application in, e.g., bistable displays [17]. This has inspired us to test experimentally whether the chiral geometry of cholesteric liquid crystals can be re-created artificially in the microscale and what optical properties such structures would exhibit. High-resolution 3D laser photolithography allowed us to fabricate arrays of twisted bands (TBs) with the characteristic dimensions in the range of micrometers, suitable for applications in the mid infrared spectral band.

First, we have recently discovered that arrays of dielectric twisted band structures reveal polarization-dependent diffraction [18]. Now, further developing this concept, in this communication we demonstrate sub-wavelength metallic structures, composed of a square grid of twisted band elements covering a metal mirror, capable of polarization manipulation in the mid-infrared. In particular, we demonstrate a device capable of converting a linear polarization of the incident infrared light into circular polarization upon normal reflection.

2 Light reflection from arrays of metal twisted bands

To gain insight into the transformation of the polarization state experienced by light upon reflection from arrays of metallic twisted bands, we resort to the finite difference time domain (FDTD) technique. In our simulations, we use MEEP 1.2.1 FDTD package [19] running on a computer cluster. Typical simulation run takes 4–5 h at a single 16-core cluster node with an Intel® Xeon® CPU E5-2670 0 @ 2.60 GHz. The 3D simulation box consists of a single twisted band element (labeled TBE in Fig. 1) built from 12 metallic rods (cuboids) with the dimensions matching our photolithographic (laser writing) setup capabilities (width × height × length = 0.3 × 1.0 × 4.0 μm3). The rod closest to the metallic substrate is half the height (0.5 μm), which reflects the geometry of the fabricated structure, where it is written halfway inside the glass substrate to ensure anchoring to the substrate. Looking from the substrate direction, each consecutive rod is rotated by 16.4° with respect to the previous one, which results in the total relative rotation between the end rods of 108°. The total height of the TB is 8 μm, and the overlap between adjacent rods along the TB axis is 0.3 μm. The twisted band element is placed on a metallic substrate and we apply periodic boundary conditions with a period of 6 μm × 6 μm in the substrate plane to account for a large array of TBs. The light source (SRC) generating short light pulses with the spectral band corresponding to vacuum wavenumbers between 900 and 2300 cm−1 is located in front of the structure. The pulses are linearly polarized in directions close to parallel to the metallic rod closest to the substrate (x). Perfectly matched layers (PMLs) are placed at both ends of the simulation box along the propagation direction (z). The spatial resolution of the simulation is 10 pixels per micron and the metallic material is modeled using the Lorentz–Drude model with the parameters for gold taken from [20]. The plasma frequency corresponds to 9.03 eV and the values of the other parameters (oscillator strengths f, frequencies ω and inverse lifetimes Γ) are listed in Table 1.

Fig. 1
figure 1

Simulation box used in the FDTD simulations. The pulsed light source SRC is placed in front of the twisted band element (TBE) and the reflected electric field components are recorded at the monitor (MON, see text for details). The substrate is perpendicular to the wave propagation direction (z). Perfectly matched layers (PMLs) are added to avoid multiple reflections

Full size image
Table 1 Oscillator strengths (f), inverse lifetimes (Γ), and frequencies (ω) for gold used in the Lorentz–Drude model.
Full size table

The electric field components of the reflected wave are recorded on the monitor (MON) and by Fourier transforming them with respect to time we retrieve the amplitude and phase of each electric field component as a function of frequency. By normalizing these to the values obtained for an empty simulation box (without the structure inside) we determine the amplitude reflection coefficient for each reflected wave component (E x and E y ) and their relative phase shift.

From thus-calculated amplitude reflection coefficients (r x , r y ) and the relative phase shift (Δφ), we obtain the polarization ellipse parameters, that is, the ellipticity (R) and the orientation (tilt) angle (T), using the following relations

$$ R = \tan (\chi ),\;\;\sin (2\chi ) = \frac{{2E_{0x} E_{0y} }}{{E_{0x}^{2} + E_{0y}^{2} }}\sin \Delta \varphi , $$
$$ \tan (2T) = \frac{{2E_{0x} E_{0y} }}{{E_{0x}^{2} - E_{0y}^{2} }}\cos \Delta \varphi . $$

In the experiments, the precise measurement of the polarization angle with respect to the structure axes is very difficult. To account for possible misalignment (rotation) of the sample relative to the incident polarization direction, during the simulations we varied the angle between the direction of the rod closest to the substrate and the incident polarization direction. Ultimately, comparing the calculated results with measured spectra, we found that the best agreement is found when this angle equals − 9°, and we calculate the orientation angle of the polarization ellipse with respect to the incoming wave polarization direction. The reflected wave ellipticity and orientation angle retrieved from the simulations within the 900–2300 cm−1 range are presented in Fig. 2. Nearly constant behavior of both the ellipticity and the polarization ellipse orientation angle over a significant range of frequencies encouraged us to attempt fabrication of a structure that could perform as a broadband waveplate.

Fig. 2
figure 2

Parameters of the reflected wave polarization ellipse—ellipticity and orientation angle—retrieved from the light propagation simulations. The twisted bands are 8 μm high (solid lines) and 7 μm high (dashed lines), and the array grid spacing is 6 μm

Full size image

3 Reflecting structure design and fabrication

The polarizing structure used in the experiments was a 100 × 100 µm grid of 8-µm-high helical twisted bands (Fig. 3). Around 300 TBs were arranged on a square grid with the lattice constant of 6 µm. Single TB consisted of several rods, each rod having 1 × 0.3 µm cross section, which results from the two-photon laser writing with a tightly focused laser beam. These dimensions are limited by the polymerization threshold of the resist and the laser power [21].

Fig. 3
figure 3

Left: 3D rendering of a single twisted band element. Right: scanning electron microscope (SEM) image of an array of twisted bands (top view, 84 × 84 µm2 field of view) with the grid spacing a = 6 µm. Around 300 of 8-µm-high, gold-coated polymer helices cover a 100 × 100 µm2 area. Insets in both pictures show a close up view of a single TB element

Full size image

Following the standard procedure of 3D laser writing [22], the structure was fabricated by photopolymerization of a liquid polymer photoresist (IP-L, Nanoscribe GmbH) on a microscope cover glass surface using a photolithographic workstation (Photonic Professional, Nanoscribe GmbH). After development in isopropanol bath for 30 min, the structure (including the base glass surface) was uniformly sputter coated with a 50-nm-thick layer of gold in a low-vacuum glow discharge sputtering coater (Q150R S, Quorum Technologies).

The polarizing properties of the structures were characterized with a Fourier transform infrared spectrometer (Tensor 37, Bruker) coupled to an optical microscope (Hyperion, Bruker). A low NA = 0.4 IR objective was used to limit the maximum incidence angles on the sample to 24°. Two broadband wire grid polarizers (5-2825, Optometrics) were used: the first one to generate linearly polarized incident beam and the second one (analyzer) to analyze the polarization state of the reflected light. Several spectra were measured in the range between 1000 and 1300 cm−1 for different orientations of the analyzer and were normalized using the reference spectrum for the light reflected from a plain, gold-coated glass substrate. Periodic functions were fitted to the data to retrieve the polarization state of the reflected beam at each wavelength, as described below. We have also printed several test structures with different geometries: the height h of 4,6,8 and 10 μm, the lattice constant a of 4, 5, 6, 7, and 8 μm, the twisted band radius r of 1.5, 1.7, 2.0, 2.4, and 3.0 μm and various orientations of the first rod with respect to the array orientation; one of them, exhibiting the most promising polarizing properties, is described in the following part (h = 8 μm, a = 6 μm, 2r = 4 μm, 13.5 ° μm−1 pitch). From the SEM measurements, we estimate the fabrication tolerances to be of the order of 0.2 μm for r and h.

4 Results and discussion

To determine the polarization state of the reflected light, we measured its intensity as a function of the analyzer angle β. The reflected electric field amplitude

$$ \vec{E}_{\text{in}} = \left( {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \alpha e^{{i\Delta_{x} }} } \\ {\sin \alpha e^{{i\Delta_{y} }} } \\ \end{array} } \right) $$

after the analyzer set at an angle β with respect to the x axis becomes proportional to

$$ \left| {\vec{E}_{\text{out}} } \right|^{2} = \frac{1}{4}(2 + \cos 2(\alpha - \beta ) + \cos 2(\alpha + \beta ) + 2\cos (\Delta_{x} - \Delta_{y} )\sin 2\alpha \sin 2\beta ). $$

From fitting this function two parameters, α and \( \delta = \Delta_{x} - \Delta_{y} \) can be retrieved that contain the information about the polarization of \( \vec{E}_{\text{in}} \). To draw the polarization ellipse in the x–y coordinates, the real values of x and y components of \( \vec{E}_{\text{in}} \) [23] are taken to obtain

$$ \left( {\frac{{E_{x} }}{\cos \alpha }} \right)^{2} + \left( {\frac{{E_{y} }}{\sin \alpha }} \right)^{2} - 2\cos \delta \frac{{E_{x} }}{\cos \alpha }\frac{{E_{y} }}{\sin \alpha } = \sin^{2} \delta , $$

where the ratio of the minor axis to the major axis (ellipticity) is

$$ R = \tan \left( {\frac{1}{2}\arcsin (\sin \delta \sin 2\alpha )} \right) $$

and the tilt angle

$$ T = \frac{1}{2}\arctan (\cos \delta \tan 2\alpha ) $$

specifies the orientation of the ellipse.

To extract the polarization state from the experimental data, we fitted the analytical formula for \( \left| {\vec{E}_{\text{out}} } \right|^{2} \) to the measured data points (reflected light intensities, compare Fig. 4b) and calculated the orientation angle and ellipticity of the reflected wave (Fig. 5b). For example for the 1080 cm−1, the ellipticity approaches one, indicating circular polarization.

Fig. 4
figure 4

a Schematic of the polarization measurement setup consisting of the infrared light source from the FTIR spectrometer, a beam splitter (BS), a microscope objective, an infrared detector and two linear polarizers, one after the source (polarizer) and one in front of the detector (analyzer). The twisted band array sample reflects light changing its polarization state, which is measured by the analyzer and the IR detector. b An example of measured normalized light intensity recorded by the IR detector as a function of the analyzer angle β. By fitting the analytical function \( \left| {\vec{E}_{\text{out}} } \right|^{2} \) to such data we retrieve the parameters of the polarization ellipse in the x–y coordinates (c) with tilt angle T specifying the ellipse orientation (tilt) and R being the ratio of the minor and major axes

Full size image
Fig. 5
figure 5

a Measured reflectance spectra of a gold-coated array of twisted bands for different angles of the analyzer (labeled on the right next to each curve, all curves normalized to a plain gold-coated sample). Insets show normalized intensity plotted as a function of the analyzer angle for two wavelengths: at 1080 cm−1 it is nearly constant, while at 1290 cm−1 the points follow a cosinusoidal pattern. b Retrieved ellipticity and orientation angle of the reflected beam as a function of the wavenumber. Insets show two examples of the measured polarization states: for 1080 cm−1 (circular) and 1290 cm−1 (an ellipse tilted by − 10° with respect to the incident linear polarization along the x axis). The resonant-like features may in part result from the undefined orientation angle for circular (and close-to-circular) polarization

Full size image

The reflectivity spectra measurements and the fitting procedures were repeated for the incident beam polarization direction between 0° and 180° (relative to the first series of measurements), and the ellipticity of the reflected light was found to change following a quarter waveplate pattern as shown in Fig. 6.

Fig. 6
figure 6

Measured ellipticity of light after reflection from the metallic TB array as a function of the wavenumber and the incident linear polarization angle. The red-shaded peaks correspond to configurations where the reflected light is circularly polarized

Full size image

While comparing the simulation results with the experimental data, some discrepancies are visible within the overall qualitative agreement. Similarly to the experimental results, the calculated orientation angle as well as the ellipticity are nearly constant across the 1100–1200 cm−1 band; however, in the simulation the latter reaches 0.5, compared to almost unity (i.e., circular polarization) in the measurements. Outside this range, in both cases, the ellipticity decreases monotonically at around 0.5/100 nm rate, while the orientation angle increases/decreases toward the long/short wavelengths, modulo the sign. We attribute the discrepancies to the fact that the absolute height of the printed twisted bands may differ from the designed value of 8 μm—careful analysis of the simulation results revealed that minute changes of this parameter lead to significant variations in both the ellipticity and the orientation angle of the reflected waves. This sensitivity of the polarizing properties to the TB arrays to the height, also present in the dielectric, diffracting structures [18], is among the known drawbacks of this design. Decreasing the TB height from 8 to 7 μm (Fig. 2, dashed lines) leads to visibly different ellipticity and orientation angle spectral characteristics.

5 Summary

In conclusion, we have presented how metallic arrays of twisted bands can be used for light polarization manipulation. In particular, a structure has been designed, fabricated, and characterized that acts as a broadband quarter waveplate (although with moderate reflectivity so far) in the mid-infrared upon normal light reflection. The structure features simple fabrication, as compared to previously demonstrated designs [6] and potential for straightforward integration into opto-electronic and photonic devices. The best broadband achromatic retarders currently available for the MIR range (made of several stacked MgF2 plates) offer the retardation uniformity as high as λ/100 over the 1700–3300 cm−1 range. They are, however, very expensive and, more importantly, operate in certain spectral bands only, due to limited selection of transparent, birefringent materials. Our design offers simple scalability, e.g., toward longer wavelengths, as well as high manufacturing flexibility—the concept of twisted bands is not limited to uniform arrays, and “patterned waveplates” can be designed, with the polarizing characteristics varying across the surface.