Skip to main content
SpringerLink
Log in

Solution of the fundamental space-filling mode of photonic crystal fibers: numerical method versus analytical approaches

  • Published:
Applied Physics B Aims and scope Submit manuscript

Abstract

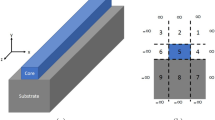
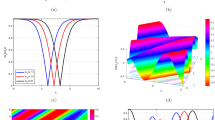
The accuracy of the solution of the fundamental space-filling mode of photonic crystal fibers by scalar and vectorial analytical approaches and its effect on the effective index models are investigated. Using a plane wave method as a benchmark, we show that the optimal choice of the radius of the equivalent circular unit cell used in the approximations is different for the two approaches and this value has a great effect on the accuracy of the solution of the fundamental space-filling mode. We also show that the vectorial approach with a properly defined value of the radius is highly accurate over a wide parameter range, whereas the scalar approach causes the main error in the scalar effective index model. We also confirm that a fully vectorial effective index model is accurate and efficient in the case of photonic crystal fibers with large air filling fractions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Bjarklev, J. Broeng, A.S. Bjarklev, Photonic Crystal Fibres (Kluwer Academic, Boston, 2003)

    Google Scholar 

  2. A. Zheltikov (ed.), Appl. Phys. B 81(2–3), 187 (2005)

    Article  ADS  Google Scholar 

  3. P. Russell, Science 299, 358 (2003)

    Article  ADS  Google Scholar 

  4. J.C. Knight, Nature 424, 847 (2003)

    Article  ADS  Google Scholar 

  5. T.A. Birks, J.C. Knight, P.S.J. Russell, Opt. Lett. 22, 961 (1997)

    ADS  Google Scholar 

  6. J.C. Knight, J. Arriaga, T.A. Birks, A. Ortigosa-Blanch, W.J. Wadsworth, P.S.J. Russell, IEEE Photon. Technol. Lett. 12, 807 (2000)

    Article  ADS  Google Scholar 

  7. N.G.R. Broderick, T.M. Monro, P.J. Bennett, D.J. Richardson, Opt. Lett. 24, 1395 (1999)

    ADS  Google Scholar 

  8. J.C. Knight, T.A. Birks, P.S.J. Russell, J.P. de Sandro, J. Opt. Soc. Am. A 15, 748 (1998)

    ADS  Google Scholar 

  9. T. Sørensen, J. Broeng, A. Bjarklev, E. Knudsen, S.E. Barkou Libori, Electron. Lett. 37, 287 (2001)

    Article  Google Scholar 

  10. R.K. Sinha S.K. Varshney, Microwave Opt. Technol. Lett. 37, 129 (2003)

    Article  Google Scholar 

  11. Y. Li, C. Wang, M. Hu, Opt. Commun. 238, 29 (2004)

    Article  ADS  Google Scholar 

  12. M. Koshiba, K. Saitoh, Opt. Lett. 29, 1739 (2004)

    Article  ADS  Google Scholar 

  13. K. Saitoh, M. Koshiba, Opt. Express 13, 267 (2005)

    Article  ADS  Google Scholar 

  14. K.N. Park, K.S. Lee, Opt. Lett. 30, 958 (2005)

    Article  ADS  Google Scholar 

  15. R.K. Sinha, A.D. Varshney, Opt. Quantum. Electron. 37, 711 (2005)

    Article  Google Scholar 

  16. F. Brechet, J. Marcou, D. Pagnoux, P. Roy, Opt. Fiber. Technol. 6, 181 (2001)

    Article  ADS  Google Scholar 

  17. Z. Zhu, T.G. Brown, Opt. Express 10, 853 (2002)

    ADS  Google Scholar 

  18. Z. Zhu, T.G. Brown, Opt. Express 8, 547 (2001)

    Article  ADS  Google Scholar 

  19. M. Midrio, M.P. Singh, C.G. Someda, J. Lightwave Technol. 18, 1031 (2000)

    Article  ADS  Google Scholar 

  20. A.W. Snyder, J.D. Love, Optical Waveguide Theory (Chapman and Hall, New York, 1983)

    Google Scholar 

  21. Y. Li, C. Wang, Z. Wang, M. Hu, L. Chai, Opt. Laser Technol., Doi: 10.1016/j.optlastec.2005.07.007 (2005)

Download references

Author information

Authors and Affiliations

  1. Ultrafast Laser Laboratory, College of Precision Instrument and Optoelectronics Engineering, Key Laboratory of Optoelectronic Information and Technical Science, Tianjin University, Tianjin, 300072, P.R. China

    Y. Li, C. Wang, Y. Chen, M. Hu, B. Liu & L. Chai

Authors
  1. Y. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. B. Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. L. Chai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Li.

Additional information

PACS

42.25.Bs; 42.70.Qs; 42.81.Qb

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Y., Wang, C., Chen, Y. et al. Solution of the fundamental space-filling mode of photonic crystal fibers: numerical method versus analytical approaches. Appl. Phys. B 85, 597–601 (2006). https://doi.org/10.1007/s00340-006-2246-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00340-006-2246-6

Keywords

Search

Navigation