1 Introduction

The laser induced ablation in a vacuum has attracted considerable attention for various space applications, such as the laser induced ablation thruster [1], laser thrust rocket launcher [1], and laser-induced breakdown spectroscopy (LIBS) [2]. A recent large low Earth orbit (LEO) constellation program used several thousand “small satellites”, which is a satellite class with a mass of a few hundred kg. Even a low failure rate means that dozens of satellites could lose control and become debris. Because they are located in an operational orbit, they pose a serious problem. Therefore, a few active debris removal (ADR) idea have been proposed, which is to tow and de-orbit debris satellites with tag-satellites similar to tugboats for shipwrecks [3] [4]. In these cases, physical contact, such as towing by wire, is a prerequisite. Mechanical coupling between satellites involves risks such as the collision between satellites and loss of attitude control at the time of coupling. In the rendezvous and docking process, the two satellites usually prepare the docking mechanisms at specific locations and exchange information about attitude and distance with each other. Both satellites control facing each other with docking mechanisms and ensure safe mechanical contact. In the case of debris capture, the attitude and distance of the debris must be identified by remote sensing. The system has not only the docking mechanism, but the satellite is also hard to make a mechanical contact with a specific surface of the debris. Mechanical contact is very difficult when the debris has high angular momentum.

On the other hand, a contactless method to deorbit debris using the thrust generated by laser ablation has been proposed [5]. In this proposal, a laser with an average power of 100 kW is required to remove debris of the order of 10 cm in a short encounter time to it. The average power of lasers for space applications that have been developed so far has at most a few 10 W. Furthermore, 100 kW of laser power requires an order of 1 MW electric power when the laser generation efficiency of 10%. Considering that International Space Station (ISS), the current largest space system, consumed about 100 kW power [6], practical application based on this concept is not realistic.

A practical system on board the small satellite has been proposed. The system rendezvous with the debris to allow longer laser irradiation period and require 100 W average laser power to deorbit the debris satellite of the order of 100 kg [7]. In this case, any contact between the debris satellite and the tag-satellite are not required. The angular momentum of the debris satellite can also be controlled, when the laser irradiating position on the debris is controlled. In this case, the greater the impulse induced by laser ablation, the more quickly for the same satellite mass, and/or large debris satellites can be deorbited within the same period. So it is important to know the efficiency and characteristics of the impulse generated by ablation in a vacuum.

In our preceding work, we measured the impulse induced by laser ablation with a Q-Switched Neodymium Doped Yttrium Aluminum Garnet (Q-SW Nd:YAG) laser at a wavelength of 1064 nm [8]. Fig. 1 shows a jet of plasma induced by the laser during our measurement. The ablation induced hot plasma expanding in the atmosphere forms a Tayler-Sedov strong spherical shock wave, the size of the expanding sphere will not exceed about 1mm in diameter [9] [10]. However, the ablation induced plasma in a vacuum freely expands in the vacuum without forming a shock wave. The jet seen in Fig. 1 is radiation from this expanding plasma, which visually extends to about 50 mm.

For the measurements, a new experimental method based on a simple pendulum was introduced. The system was found to have a resolution of \(10^{-7}\)Ns for ablation events induced by a single laser at a pulse rate of 2 Hz or less. For ablation events at a pulse rate of 10 Hz and above, the system recorded the impulse as an average force. The impulse generated by the Nd:YAG laser irradiating A7075 aluminum alloy was investigated. The impulse was generated at 3 J/cm\({}^2\), and the momentum coupling factor plateaued to approximately \(20 \mu\)Ns/J over a range of 5–50 J/cm\(^2\) without producing a plasma shielding effect. This result highlights that it should be feasible to deorbit a 150 kg abandoned satellite at an altitude of 1000km using a chaser satellite equipped with a 100W laser [8]. The orbit change of the spacecraft is characterized by the velocity change, the so-called “Delta V”, \(\Delta V = {m_s}/{p_t}\), where \(m_s\) and \(p_t\) are the mass of the spacecraft and total impulse, respectively. Efficient impulse generation means that the heavier space debris will be cleaned in a shorter period, or that the system will be appropriate for smaller spacecraft. The momentum coupling factor \(C_m\) is the ratio of the propulsive impulse to the irradiation laser power. The larger the momentum coupling factor, the more efficiently debris can be removed with the same laser power. The generation and heating process of ablation plasma depends on the pulse width through the range from femtoseconds, picoseconds, and nanoseconds, and it is expected to have a significant impact on the coupling coefficient. However, the first high power Q-SW Nd:YAG space laser was demonstrated by Lidar In-Space Technology Experiment (LITE) on board Space shuttle STS-65 [11], and several spaceborne laser missions including planetary exploration missions, for example, Mars Orbiter Laser Altimeter (MOLA) [12] and Lunar Orbiter Laser Altimeter (LOLA) [13], followed. Except for Advanced Topographic Laser Altimeter System (ATLAS) [14] which employed a pulsed fiber laser on board ICESat2, most space missions utilize Q-SW Nd:YAG lasers. In particular, the space lidar systems for atmospheric observation such as Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) [15], Atmospheric Laser Doppler Instrument (ALADIN) [16], and Atmospheric Lidar (ATLID) [17] use not only the fundamental wave of the Nd:YAG laser but also second harmonic generation (SHG) and third harmonic generation (THG), which can be generated using nonlinear crystals. Based on the above current status of space lasers, we evaluated the characteristics of Nd:YAG fundamental and SHG. The rest of this paper is structured as follows. In Sect. 2, we detail the instrumental setup of our experiment. Section 3 describes both the impulse measurement and the nonlinear effect, followed by concluding remarks in Sect. 4.

Fig. 1
figure 1

The impulse of the Nd:YAG Q-switched laser is measured by the impulse stand

Full size image

2 Instrument setup

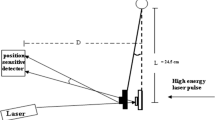
The instrumentation of the impulse measurement system is shown in Fig. 2. The second harmonics of the Nd:YAG laser is generated by a KD*P nonlinear crystal, which is then separated by a dichroic beam splitter. This part of the system is installed in a SPECTRA-PHYSICS GCR-230 pulsed Nd:YAG laser. The fundamental (1064nm) and SHG (532nm) beams are attenuated by the \(\lambda /2\) wave plate (2) and polarizing beam splitting prism (3), respectively. Each beam is focused on the target of the impulse stand (12) [8] by its adjustable beam expander (7). Each illuminated spot size is tuned through the focusing of the expander. The two beams of different wavelengths can be overlapped by the dichroic mirror (9). Energy meters (6) record the energy of every laser pulse, which are calibrated by the irradiated energy on the target to compensate for the loss of the optical components through the beam path. Ophir PE50BF-C and PE25BF-C are used for 1064 nm and 532 nm, respectively. The beam spots of 1064 nm and 532 nm are then redirected by the high reflection mirror (8) and the beam combiner (9), respectively. The high reflection mirror (10) controls both beams without requiring their relative positions.

The spot size on the target and attenuation of the laser beam can tune the fluence on the target, which is usually measured by attenuator scanning. The various spot size data should be combined to obtain a wide range of data regarding fluence.

An achromatic lens (13) and beam profiler (15) monitor the spot of the irradiated laser on the target and the emission of the ablation-induced plasma with a small focus shift from visible to infrared. A filter assembly (14) has a short pass filter, 1064nm narrow band filter, 532 nm narrow band filter, 532nm band rejection filter, and ND filter to observe fundamental, SHG, and ablation-induced emission separately. A combination of the 532nm band rejection and the short pass filter enables the emission to be monitored. The actual irradiated beam size is measured using the ablation mark under microscopy to obtain the laser fluence from the pulse energy. A top-hat beam profile is used to expect uniform fluence in the irradiated position. In addition, the irradiation position is defocused so large that the focal point size is on the order of 1mm. Since the defocus is large and the beam spot size of 1mm is so large that the beam waist is negligible, the beam spot shape is obtained by geometric optics and the radiated spot is obtained as a similarly reduced form of a near fielded profile. As a result, the near field top-hat pattern is directly transferred onto the irradiation target [8]. A comparison between the beam profile and the ablation mark confirms that ablation occurs throughout the beam, and the ablation mark is used as the most reliable beam size on the irradiation surface.

The impulse stand can be self-calibrated using a solenoid magnet [8], and the accuracy has been estimated to be better than 0.5%. Using the same calibration system, the resolution for single pulses has been confirmed to be \(0.03\mu\)Ns in root mean square (rms).

The GCR-230 is tuned to be a good performance at the operating condition of over 10 W output power for 10 to 20 Hz. The flash lamps and Q-switch are synchronously triggered at 10Hz and 1Hz, respectively, for GCR-230 laser operation, and the 1Hz laser shots with top-hat beam profile are obtained. Since GCR-230 with 1 Hz flash lamp operation for previous work had outer edge enhanced beam profile probably caused by the improper thermal lens due to the small average heat input to Nd:YAG medium, the beam shaping aperture was used to obtain top-hat beam [8]. The aperture has no longer necessary and is removed from the current instrument setup.

Fig. 2
figure 2

Diagram of the impulse measurement instruments. (1)SHG unit with beam separator as part of the GCR-230 laser, (2) \(\lambda /2\) wave plate, (3) Polarizing beam splitter,(4) Beam splitter, (5) Beam damper, (6) Energy meter, (7) Beam expander and focus adjuster, (8, 10, 11) High reflection mirrors, (9) Dichroic beam combiner, (12) Impulse stand, (13) Achromatic imaging lens, (14) Filter assembly, and (15) Beam profiler

Full size image

3 Measurements

3.1 Impulse measurement

Impulse measurements were performed for the 532 nm beam by blocking the 1064 nm beam. Fig. 3 shows the momentum coupling factor \(C_m\) as a function of fluence of the 532 nm pulse, together with the data of 1064 nm pulses which were obtained in our previous work [8].

In the initial measurement of ablation impulses targeting aluminum [18], a nonlinear increase with saturation in impulse with increasing irradiation was exhibited. This effect corresponds in \(C_m\) as a linear decrease from \(20\mu\)Ns/J to \(15\mu\)Ns/J for an increase in fluence from 5 to 15 J/cm\({}^2\). This decrease in \(C_m\) is discussed as ablation suppression due to the plasma shielding effect. No attention was paid to the beam profile in this measurement, only to the beam diameter of the laser, which was measured on laser burn-paper. For example, a Gaussian beam profile would contain 86% of the total beam energy in the \(e^{-2}\) diameter, but there is about an 8-fold fluence variation within the beam. In such a beam, ablation begins when the peak fluence in the beam exceeds the threshold, and only a fraction of the total beam energy contributes to ablation. As a result, impulse generation near the ablation threshold may be expected to behave in a complicated manner if the beam profile is not uniform. In the case of a laser with a non-uniform profile, the high mass removal rate in the high fluence part, the central part for above Gaussian profile, may make a deep crater. Tsuruta et al. [19] discussed the effect of the engraved craters and found the deeper crater generated less impulse. They removed the crater effects and obtained a similar result, a linear decrease from \(20\mu\)Ns/J to \(15\mu\)Ns/J for an increase from 5 to 25 J/cm\({}^2\).

To exclude such conditions in our work, the uniform profile on the irradiated surface shall be obtained using top-hat profile laser and the aspect ratio of the crater shall be less than 0.1. As a result, in Fig. 3, the decrease of \(C_m\) with increasing fluence, the so-called plasma shielding effect, is not observed.

According to the instrument resolution, the random deviation due to the instruments for \(C_m\) of the measurement is estimated to be less than \(0.3 \mu\)Ns/J though the entire measured fluence range for the 1064 nm measurement. For 532nm, it is estimated to be less than \(1.5\mu\)Ns/J, because the laser pulse energy is smaller than that of 1064nm. The random deviation of the data is considered as the variation due to impulse generation itself. Each data set in Fig. 3 consists of several to a few dozen fluence scanning, low to high and high to low, track data. Based on the apparent deviation among the tracks, uncontrollable repeatability error of \(C_m\) is roughly estimated at a few 10% which may be possible residual effects of laser profile nonuniformity and the crater effects. Since these effects could not be identified and removed, s simple model is assumed from all data to estimate the overall behavior.

As good linearity is expected for the generated impulse and irradiating fluence, Equ. 1 was fitted to all obtained data,

$$\begin{aligned} C_m = {\left\{ \begin{array}{ll} \frac{S_m (\phi - \phi _{th})}{\phi } &{} \text{ if } ~ \phi - \phi _{th} \ge 0\\ 0 &{} \text{ if } ~ \phi - \phi _{th} < 0, \end{array}\right. } \end{aligned}$$
(1)

where \(\phi\), \(\phi _{th}\), and \(S_m\) are the irradiation fluence, fluence threshold, and the momentum coupling slope coefficient, respectively. The fitted functions are plotted in Fig. 3. The fitted residuals are \(3.3\mu\)Ns/J and \(3.0\mu\)Ns/J in root mean square, respectively for 1064 nm and 532 nm. This means that the models are acceptable when the above measurement errors are assumed, which are consistent value repeatability errors of a few ten percent for this measurement. Therefore, this measurement shows that no \(C_m\) decrease due to the so-called plasma shielding effect is observed in the fluence less than 50 J/cm\({}^2\).

The threshold fluence of 1.1J/cm\({}^{-2}\) and, the slope coefficient of 23 \(\mu\)Ns/J for 1064nm are obtained, and 0.6J/cm\({}^{-2}\) and 31 \(\mu\)Ns/J are obtained at 532nm. The threshold at which ablation occurs is lower for 532 nm compared to 1064 nm. This behaviour is consistent with D’Souza’s results [20]. The ablation rate, mass loss rate, at 532 nm is about 20 times higher than at 1064 nm, which is consistent with a large ejecta mass contributing to a largely generated impulse [21].

Fig. 3
figure 3

Measured momentum coupling factor \(C_m\). Three cases of Nd:YAG fundamental data (1064 nm) are replicated from previous work [8]. The momentum coupling factor of 532 nm shows a lower threshold and higher value than that of 1064nm. The solid lines show the fitted functions described by Equ. 1

Full size image
Fig. 4
figure 4

Measured momentum coupling factor \(C_m\) for a copper target for 1064 nm and 532 nm laser irradiation

Full size image

Fig. 4 shows the measured \(C_m\) for a C10200 oxygen-free copper (OFC) target. The copper data covers a relatively narrower region than the previous stitched aluminum alloy data. In this measurement, the irradiating laser energy was scanned by about one order of magnitude and no fluence stitching was performed by changing the spot size. In particular, at 532 nm, random errors in the measurement system dominate for the lower fluence region, since the maximum laser energy is only 70 mJ. The resolution was inversely proportional to fluence and was estimated to be 5muNs/J at 1 J/cm2. For 1064 nm, the same order of impulse to the 532nm case is expected due to the smaller \(C_m\), though the laser peak energy is about 3 times larger than that of 532nm. the measurement system error is a similar formula to the 532nm case with \(0.5\mu\)Ns/J at 10J/cm\({^2}\). The threshold fluence and the slope factor of \(2.7\pm 0.7\)J/cm\({}^{-2}\) and \(14\pm 1\) \(\mu\)Ns/J for 1064nm and \(0.24\pm 0.4\)J/cm\({}^{-2}\) and \(25\pm 4\) \(\mu\)Ns/J for 532nm, are obtained respectively. At 1064 nm, a higher threshold and smaller \(C_m\) are observed for copper than aluminum. At 532 nm, no clear threshold difference was observed between copper and aluminum, but \(C_m\) at 532 nm is about 1.8 times higher than at 1064 nm. Compared to D’Souza’s measurements, the results are generally consistent except for the threshold for copper at 532 nm. Also, at 1064 nm, the \(C_m\) decrease at high fluences is not observed, which is consistent with the present results. The ablation threshold at 532 nm is larger than that for aluminum, which is inconsistent with the present study. In this study, the repeatability error as shown in the aluminum case is not taken account. Additional measurements to improve statistic error as well as taking account of the repeatable error are expected for further discussion.

The reflectance of copper at 1064 and 532nm is 98% and 60%, respectively, while for aluminum it is 95% and 92%, respectively [22]. The difference in ablation threshold is consistent with the reflectance dependence for both 1064 nm and 532 nm, where a material with high reflectivity that absorbs less laser energy has a higher threshold. However, at 1064nm, copper has a larger reflectivity and acquires less energy than aluminum, with a smaller \(C_m\). At 532 nm, copper, which has a smaller reflectivity, has a slightly smaller \(C_m\), and it is therefore not only the amount of energy absorbed by the material that determines the laser-induced impulse.

In the case of a nanosecond laser, ablation is initiated by free electrons heating in a metal due to the electric field of laser radiation. The heat from the higher energy electrons is transferred to the crystal lattice meaning the metal melts, evaporates, and some part of which is ionized to form plasma [23]. Copper has approximately 1.7 times higher thermal conductivity than aluminum, which reduces temperature rise and evaporation. Smaller copper \(C_m\) than that of aluminum at both the 1064 nm and 523 nm may be mainly caused by the difference in ejected mass. The laser irradiation heats the plasma by inverse bremsstrahlung. Plasma formation and heating proceed simultaneously in nano second order. In the case of very high laser fluence, the plasma strongly absorbs the radiation so that material evaporation is suppressed. In this region, \(C_m\) decreases with a higher fluence, which is identified as the so-called plasma shielding effect [1]. The \(C_m\) plateau above approximately one order of the fluence region above a slightly higher ablation threshold, as shown in Figs. 3 and 4, highlights how the distribution ratio of laser energy used for plasma formation and plasma heating is constant for this specific material and wavelength. In this region, so-called plasma shielding, decreasing in \(C_m\), is not observed and ablation induced plasma characteristics, such as plasma temperature and density and so on, on the nanosecond timescale should be investigated to understand the behavior of laser induced impulse.

3.2 Nonlinear effect

Laser ablation using an Nd: YAG laser targeting aluminum has measured the generation of high-temperature plasma of several tens of eV [24]. Because the heating rate of inverse bremsstrahlung has strong wavelength-dependence, i.e., \(\propto \lambda ^4\) for high temperature plasma [25], 532 nm radiation has a less efficient plasma heating effect than 1064 nm. Because \(C_m\) is on the same order of magnitude at 1064 nm and 532 nm for the same material, we can infer that a larger amount of material is evaporated in the 532 nm ablation than in 1064 nm, but this occurs at a lower temperature and with lower heating efficiency. When a large amount of material evaporated at 532 nm can be efficiently heated by radiation at 1064 nm, by irradiating two wavelengths simultaneously, a high \(C_m\) can be obtained.

Generated impulses can be represented by \(p = m_a v_e \propto m_a \sqrt{T_p}\), where \(m_a\), \(v_e\), \(T_p\) are the mass, mean velocity, and the mean temperature of the total ablated material. Since Some parts of the ablated material may not be ionized and the formed plasma may be recombined through expansion, the temperature and velocity may be considered the average value of the ablated gas containing the neutral and plasma, but it should be possible to discuss it in relation to the plasma produced within the laser irradiation time. Anyway, the higher temperature gas will be formed by the more efficient plasma heating. The impulse transferred by dual wavelength irradiation to the target can be expressed by Equ. 2. Assuming that plasma generation \(m_a\) is proportional to the 532 nm irradiation and that the heating energy \(T_p\) is proportional to 1064 nm, the lowest order cross term will be proportional to \(E_{532}E_{1064}\). Therefore, the following nonlinear effect is expected.

$$\begin{aligned}&p= C_{m,532}E_{532} + C_{m,1064}E_{1064}\nonumber \\&\quad + M_{m,532,1064}E_{532}E_{1064}. \end{aligned}$$
(2)
$$\begin{aligned}&E_{total}= E_{532}+ E_{1064}, \end{aligned}$$
(3)

where \(C_{m,532}\), and \(C_{m,1064}\) are the momentum coupling factors for 532 nm and 1064 nm, respectively. \(E_{total}\) is the fundamental laser energy input to the nonlinear SHG crystal, and \(E_{532}\) is SHG laser energy. \(E_{1064}\) is SHG residual energy radiated on the target. \(M_{m,532,1064}\) is the nonlinear constant.

Without the cross term, the equation is deduced to the simple superposition of two beams without any interference. The effective momentum conversion factor would be the weighted averages of the \(C_m\) values for each wavelength. A preliminary two-beam superimposed experiment in which the impulse was measured in similar way to obtain Fig. 3 with and without SHG irradiation showed no apparent nonlinear coefficient \(M_{m,532,1064}.\) As mentioned in the estimation of ablation threshold fluence and slope coefficient, the measured impulse data may contain a possible systematic repeatability error of the order of 10 % due to the influence of beam uniformity and the engraved crater. The parameters \(C_{m,532}\), \(C_{m,1064}\), and \(M_{m,532,1064}\) cannot be obviously determined over the repeatability error by the above approach, and the experiment focused on detecting the nonlinear effect is conducted.

The third term of the equation can be measured directly free from the effect of the beam profile and the crater. The two beams shown in Fig. 2 are activated simultaneously and irradiated onto the target on the impulse stand. The alignment of the mirrors was adjusted, and the irradiation positions of the 532 nm beams were adjusted, first individually, then irradiating the same point, and then again separately. In this demonstration, the laser beam profiles are constant in time and the effect of the crater is confirmed to be the same by comparing the impulse before and after the superposed measurement. The irradiated laser energy of 1064 nm and 532 nm are 356 mJ and 78 mJ, respectively. The results showed a 5% excess for the third term, as shown in the figure, which confirms the existence of a nonlinear term (Fig. 5).

Fig. 5
figure 5

 Relationship between the laser irradiated positions observed by ablation induced visible light and the generated total impulse. Initially, two beams of 1064 nm and 532 nm are simultaneously irradiated onto different positions. The 532 nm beam was subsequently directed to the 1064 nm position and then separated again. Total impulse is measured continuously

Full size image

4 Conclusion

In this study, we investigated the application of laser ablation for the removal of space debris. Because most of the high-power lasers currently utilized in space-based applications are Nd:YAG lasers, we examined the characteristics of SHG from a KD*P nonlinear crystal. The momentum coupling factor of 1064 nm and its SHG 532 nm for an aluminum alloy A7075 and C10200 OFC were measured. Both materials show a lower threshold fluence and larger momentum coupling factor at 532 nm.

As a method to efficiently generate impulses with the same laser energy, the use of SHG to irradiate the same point with a fundamental residual laser 1064 nm is presented. A nonlinear effect due to the interaction of the two wavelength beams has been directly demonstrated, but the effect on copper was not so useful in the debris cleaning mission, at only 5%. Further research needs to be conducted on the generation of nonlinear terms. Even without the third term in Equ. 2, dual beam irradiation provides a higher impulse than the impulse \(p=C_{m,1064}E_{total}\) without SHG. SHG does not require additional power-consuming active equipment such as additional exciters or amplifiers but requite temperature-controlled nonlinear crystals, and impulses can be increased with minimal additional power. It turned out to be advantageous for space applications, which will keep the operational power at a minimum.